I UM J O ID VE ĀRA —

I UM J O ID VE ĀRA - 2. P T IEJ E V S K ISŽ I D A R ET S P O V OM L A E IS Ģ LAD V

TEORIJA 1 Paralēlā pārnese. 2 Aksiālā simetrija. 3 Pagrieziens. 4 Homotētija.

PARALĒLĀ PĀRNESE Paralēlo pārnesi nosaka vektors, pa kuru šo pārnesi izdara. Lai veiktu paralēlo pārnesi, ir jāzina virziens un attālums. Par figūru paralēlo pārnesi sauc attēlojumu, kurā katrs figūras punkts pārvietojas vienā un tajā pašā virzienā par vienu un to pašu attālumu. Lai paralēlajā pārnesē konstruētu daudzstūra attēlu, pietiek konstruēt tā virsotņu attēlus

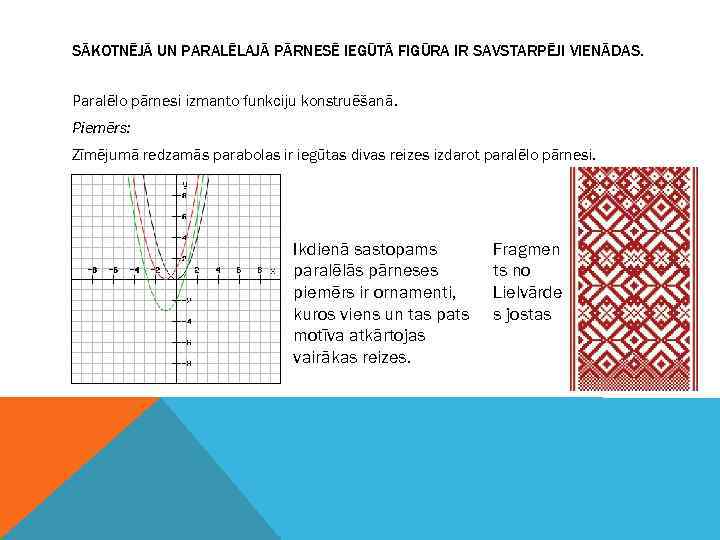SĀKOTNĒJĀ UN PARALĒLAJĀ PĀRNESĒ IEGŪTĀ FIGŪRA IR SAVSTARPĒJI VIENĀDAS. Paralēlo pārnesi izmanto funkciju konstruēšanā. Piemērs: Zīmējumā redzamās parabolas ir iegūtas divas reizes izdarot paralēlo pārnesi. Ikdienā sastopams paralēlās pārneses piemērs ir ornamenti, kuros viens un tas pats motīva atkārtojas vairākas reizes. Fragmen ts no Lielvārde s jostas

AKSIĀLĀ SIMETRIJA Divus punktus A un B sauc par simetriskiem attiecībā pret taisni t, ja šī taisne ir perpendikulāra nogrieznim AB un iet caur tā viduspunktu. Divas figūras sauc par simetriskām attiecībā pret taisni, ja katrs pirmās figūras punkts attēlojas par tam simetrisku otrās figūras punktu (un otrādi). Taisni t tad sauc par simetrijas asi. Lai aksiālā simetrija būtu definēta, jābūt uzdotai simetrijas asij. Aksiāli simetriskas figūras ir savstarpēji vienādas. Aksiālo simetriju dažkārt izmanto, lai konstruētu funkciju grafikus. Pāra funkcijas ir simetriskas pret Oy asi.

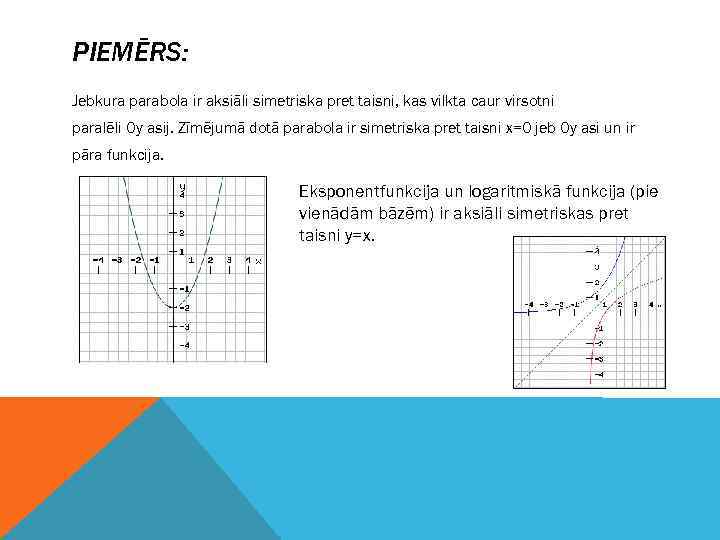PIEMĒRS: Jebkura parabola ir aksiāli simetriska pret taisni, kas vilkta caur virsotni paralēli Oy asij. Zīmējumā dotā parabola ir simetriska pret taisni x=0 jeb Oy asi un ir pāra funkcija. Eksponentfunkcija un logaritmiskā funkcija (pie vienādām bāzēm) ir aksiāli simetriskas pret taisni y=x.

. FRAGMENTS NO LIELVĀRDES JOSTAS AKSIĀLĀ SIMETRIJA DABĀ

PAGRIEZIENS Ja viena figūra iegūta no otras figūras, tās visus punktus pagriežot ap centru O par noteiktu leņķi, tad šādu figūras pārvietojumu sauc par pagriezienu. Lai pagrieziens būtu definēts, jābūt uzdotam pagrieziena centram. O un pagrieziena leņķim α. Pretēji pulksteņa rādītāju virzienam ir pozitīva pagrieziena leņķis, otrādi negatīvs pagrieziena leņķis (tāpat kā pagrieziena leņķi vienības riņķī).

PIEMĒRS: TRIJSTŪRIS PAGRIEZTS POZITĪVĀ VIRZIENĀ (APMĒRAM PAR 30 GRĀDIEM): . Ja pagrieziena leņķis ir 180 vai − 180 grādi, tad figūra attēlojas par tai centrāli simetrisku figūru un šo pagriezienu sauc par centrālo simetriju.

. . Punkts A ir centrāli simetrisks punktam B. Ornamentos bieži sastopams pagrieziens par 90 un 180 grādiem.

HOMOTĒTIJA Homotētija ir līdzības vispārinājums. Tas ir pārveidojums, kurā iegūst līdzīgas figūras (figūras, kuru atbilstošie leņķi ir vienādi un malas ir proporcionālas). Homotētiskām figūrām ir spēkā līdzīgu figūru laukumu attiecības formula S 1 S 2=k 2. Interesanti: jebkuras divas riņķa līnijas ir homotētiskas. Lai homotētija būtu definēta, jābūt uzdotam homotētijas centram. O un koeficientamk. To var pierakstīt šādi: homotētija (O; k). Zīmējumā no figūras F 1 var iegūt figūru F 2 ar homotētiju (O; 2). Homotētija ar centru O un koeficientu k ir pārveidojums, kurā katrs punkts P attēlojas par tādu punktu P 1, ka OP 1−→−=k⋅OP−→, kur k≠ 0.

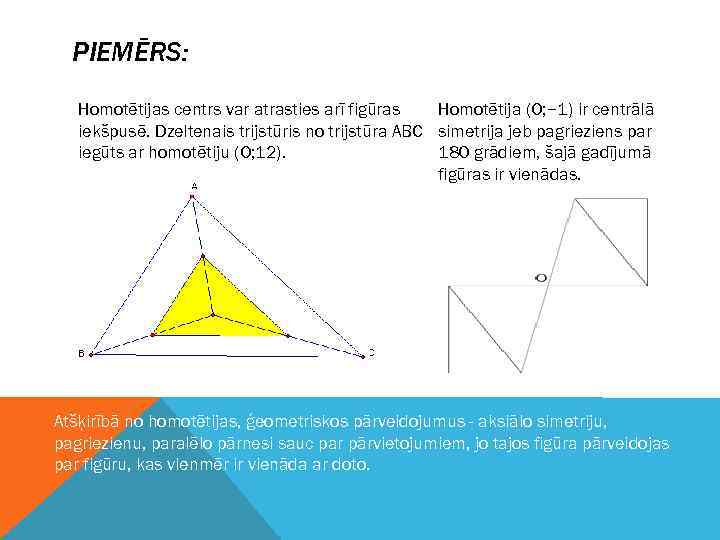PIEMĒRS: . Homotētijas centrs var atrasties arī figūras Homotētija (O; − 1) ir centrālā iekšpusē. Dzeltenais trijstūris no trijstūra ABC simetrija jeb pagrieziens par iegūts ar homotētiju (O; 12). 180 grādiem, šajā gadījumā figūras ir vienādas. Atšķirībā no homotētijas, ģeometriskos pārveidojumus - aksiālo simetriju, pagriezienu, paralēlo pārnesi sauc par pārvietojumiem, jo tajos figūra pārveidojas par figūru, kas vienmēr ir vienāda ar doto.

. Homotētiskas figūras ir līdzīgas, bet līdzīgas figūras ne vienmēr ir homotētiskas. (homotētijā ir svarīgs arī figūru novietojums). Fraktāļos var redzēt bezgalīgi daudz līdzīgas figūras, bet tās parasti nav homotētiskas, jo tām nevar noteikt homotētijas centru.

. Uzdevumi. lv Google. lv