I Portable Extensible Toolkit for Scientific Computation Boyana

I. Portable, Extensible Toolkit for Scientific Computation Boyana Norris (representing the PETSc team) Mathematics and Computer Science Division Argonne National Laboratory, USA March, 2009 1

What is PETSc? n n n A freely available and supported research code Download from http: //www. mcs. anl. gov/petsc Hyperlinked manual, examples, and manual pages for all routines Hundreds of tutorial-style examples, many are real applications Support via email: petsc-maint@mcs. anl. gov Usable from C, C++, Fortran 77/90, and Python 2

What is PETSc? n Portable to any parallel system supporting MPI, including: – Tightly coupled systems • Blue Gene/P, Cray XT 4, Cray T 3 E, SGI Origin, IBM SP, HP 9000, Sub Enterprise – Loosely coupled systems, such as networks of workstations • Compaq, HP, IBM, SGI, Sun, PCs running Linux or Windows, Mac OS X n PETSc History – Begun September 1991 – Over 20, 000 downloads since 1995 (version 2), currently 300 per month n PETSc Funding and Support – Department of Energy • Sci. DAC, MICS Program, INL Reactor Program – National Science Foundation • CIG, CISE, Multidisciplinary Challenge Program 3

How did PETSc Originate? PETSc was developed as a Platform for Experimentation. We want to experiment with different • Models • Discretizations • Solvers • Algorithms (which blur these boundaries)

Successfully Transitioned from Basic Research to Common Community Tool n Applications of PETSc – – – – Nano-simulations (20) Biology/Medical(28) Cardiology Imaging and Surgery Fusion (10) Geosciences (20) Environmental/Subsurface Flow (26) Computational Fluid Dynamics (49) Wave propagation and the Helmholz equation (12) Optimization (7) Other Application Areas (68) Software packages that use or interface to PETSc (30) Software engineering (30) Algorithm analysis and design (48) 6

The Role of PETSc Developing parallel, nontrivial PDE solvers that deliver high performance is still difficult and requires months (or even years) of concentrated effort. PETSc is a tool that can ease these difficulties and reduce the development time, but it is not a black-box PDE solver, nor a silver bullet. 8

Features n n n n Many (parallel) vector/array operations Numerous (parallel) matrix formats and operations Numerous linear solvers Nonlinear solvers Limited ODE integrators Limited parallel grid/data management Common interface for most DOE solver software 9

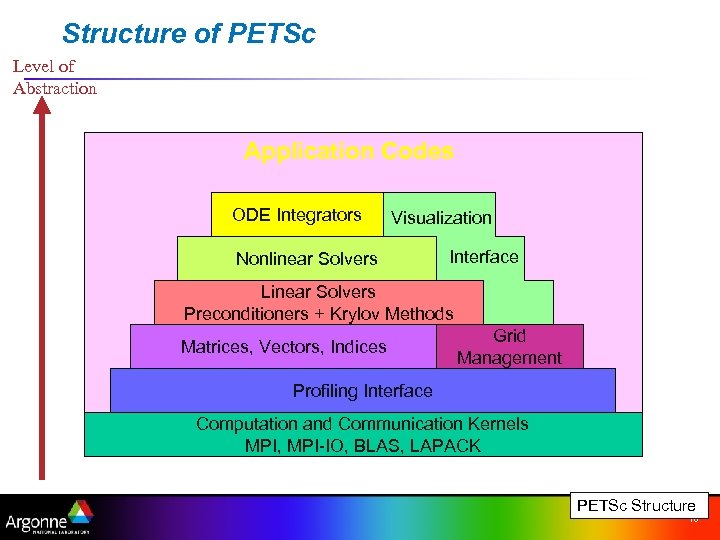
Structure of PETSc Level of Abstraction Application Codes ODE Integrators Visualization Nonlinear Solvers Interface Linear Solvers Preconditioners + Krylov Methods Matrices, Vectors, Indices Grid Management Profiling Interface Computation and Communication Kernels MPI, MPI-IO, BLAS, LAPACK PETSc Structure 10

The PETSc Programming Model n Distributed memory, “shared-nothing” • Requires only a standard compiler • Access to data on remote machines through MPI n Hide within objects the details of the communication n User orchestrates communication at a higher abstract level than direct MPI calls PETSc Structure 24

Getting Started Petsc. Initialize(); Obj. Create(MPI_comm, &obj); Obj. Set. Type(obj, ); Obj. Set. From. Options(obj, ); Obj. Solve(obj, ); Obj. Getxxx(obj, ); Obj. Destroy(obj); Petsc. Finalize() Integration 25

PETSc Numerical Components Nonlinear Solvers (SNES) Newton-based Methods Line Search Trust Region Time Steppers (TS) Other Backward Pseudo Time Euler Stepping Euler Other Krylov Subspace Methods (KSP) GMRES Additive Schwartz CG Block Jacobi CGS Bi-CG-STAB TFQMR Richardson Chebychev Preconditioners (PC) Jacobi ILU ICC Other LU (Sequential only) Others Matrix-free Other Matrices (Mat) Compressed Sparse Row (AIJ) Blocked Compressed Sparse Row (BAIJ) Block Diagonal (BDIAG) Distributed Arrays(DA) Dense Index Sets (IS) Indices Block Indices Stride Other Vectors (Vec) 26

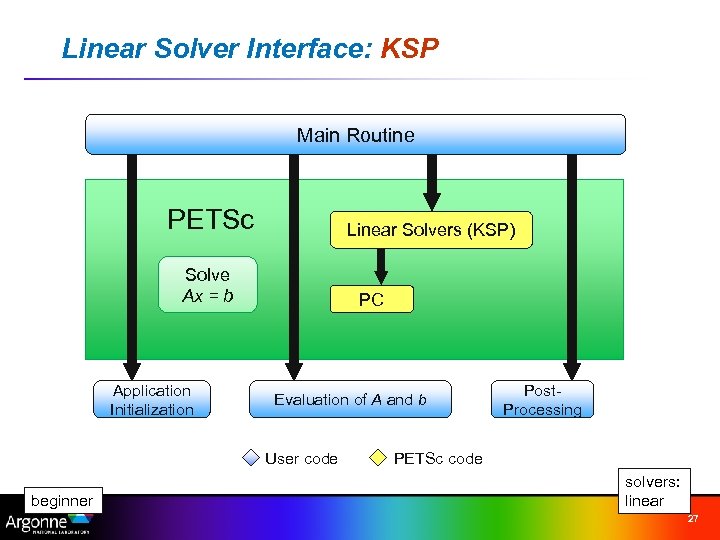
Linear Solver Interface: KSP Main Routine PETSc Linear Solvers (KSP) Solve Ax = b Application Initialization PC Evaluation of A and b User code beginner Post. Processing PETSc code solvers: linear 27

Setting Solver Options at Runtime n -ksp_type [cg, gmres, bcgs, tfqmr, …] n -pc_type [lu, ilu, jacobi, sor, asm, …] 1 2 n -ksp_max_it <max_iters> n -ksp_gmres_restart <restart> n -pc_asm_overlap <overlap> n -pc_asm_type [basic, restrict, interpolate, none] n etc. . . 1 2 beginner intermediate solvers: linear 28

Recursion: Specifying Solvers for Schwarz Preconditioner Blocks n Specify KSP solvers and options with “-sub” prefix, e. g. , – Full or incomplete factorization • -sub_pc_type lu • -sub_pc_type ilu -sub_pc_ilu_levels <levels> – Can also use inner Krylov iterations, e. g. , • -sub_ksp_type gmres -sub_ksp_rtol <rtol> • -sub_ksp_max_it <maxit> beginner solvers: linear: preconditioners 29

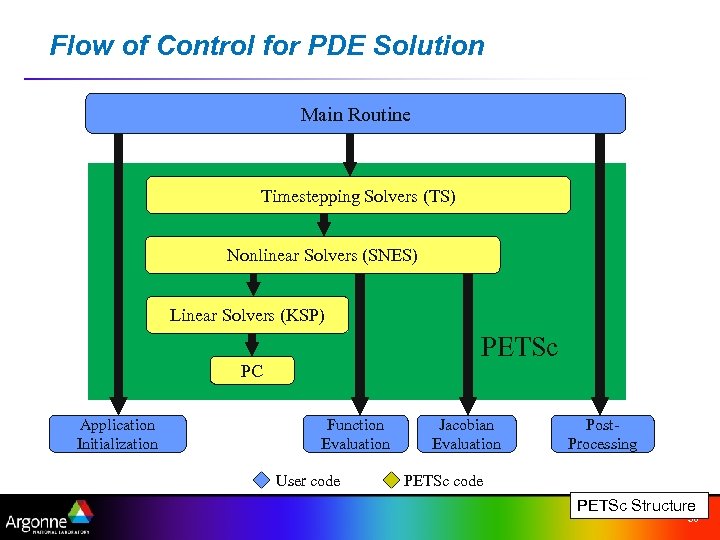
Flow of Control for PDE Solution Main Routine Timestepping Solvers (TS) Nonlinear Solvers (SNES) Linear Solvers (KSP) PETSc PC Application Initialization Function Evaluation User code Jacobian Evaluation Post. Processing PETSc code PETSc Structure 30

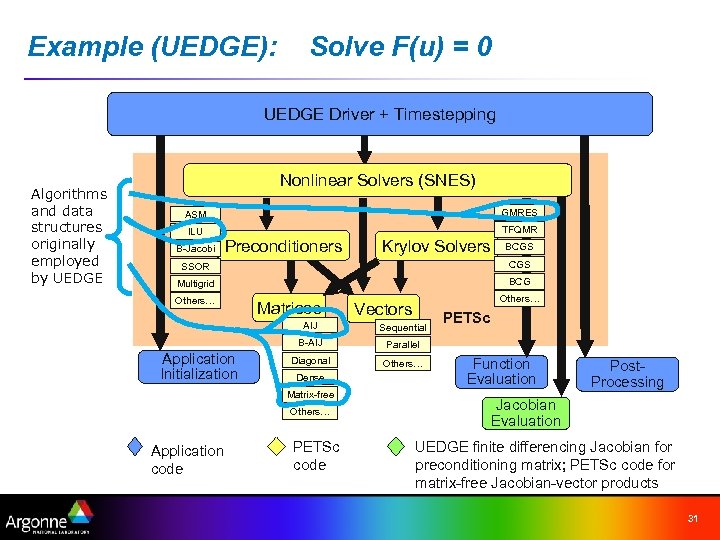
Example (UEDGE): Solve F(u) = 0 UEDGE Driver + Timestepping Algorithms and data structures originally employed by UEDGE Nonlinear Solvers (SNES) ASM GMRES ILU TFQMR B-Jacobi Preconditioners Krylov Solvers BCGS SSOR CGS Multigrid BCG Others… Matrices Others… Vectors AIJ B-AIJ Application Initialization Sequential Parallel Diagonal Others… Dense Matrix-free Others… Application code PETSc code Function Evaluation Post. Processing Jacobian Evaluation UEDGE finite differencing Jacobian for preconditioning matrix; PETSc code for matrix-free Jacobian-vector products 31

Nonlinear Solver Interface: SNES Goal: For problems arising from PDEs, support the general solution of F(u) = 0 User provides: – Code to evaluate F(u) – Code to evaluate Jacobian of F(u) (optional) • or use sparse finite difference approximation • or use automatic differentiation – AD support via collaboration with P. Hovland B. Norris – Coming in next PETSc release via automated interface to ADIFOR and ADIC (see http: //www. mcs. anl. gov/autodiff) solvers: nonlinear 32

SNES: Review of Basic Usage n SNESCreate( ) - Create SNES context n SNESSet. Function( ) - Set function eval. routine n SNESSet. Jacobian( ) - Set Jacobian eval. routine n SNESSet. From. Options( ) - Set runtime solver options for [SNES, SLES, KSP, PC] n SNESSolve( ) - Run nonlinear solver n SNESView( ) - View solver options actually used at runtime (alternative: snes_view) solvers: nonlinear n SNESDestroy( ) - Destroy solver 33

Uniform access to all linear and nonlinear solvers n -ksp_type [cg, gmres, bcgs, tfqmr, …] n -pc_type [lu, ilu, jacobi, sor, asm, …] n -snes_type [ls, …] n -snes_line_search <line search method> n -sles_ls <parameters> n -snes_convergence <tolerance> n etc. . . 1 2 solvers: nonlinear 34

PETSc Programming Aids n Correctness Debugging – Automatic generation of tracebacks – Detecting memory corruption and leaks – Optional user-defined error handlers n Performance Profiling – Integrated profiling using -log_summary – Profiling by stages of an application – User-defined events Integration 35

Ongoing Research and Developments n Framework for unstructured meshes and functions defined over them n Framework for multi-model algebraic system n Bypassing the sparse matrix memory bandwidth bottleneck – Large number of processors (nproc =1 k, 10 k, …) – Peta-scale performance n Parallel Fast Poisson Solver n More TS methods n… 36

Framework for Meshes and Functions Defined over Them n The PETSc DA class is a topology and discretization interface. – Structured grid interface • Fixed simple topology – Supports stencils, communication, reordering • Limited idea of operators n The PETSc Mesh class is a topology interface – Unstructured grid interface • Arbitrary topology and element shape – Supports partitioning, distribution, and global orders 37

Parallel Data Layout and Ghost Values: Usage Concepts Managing field data layout and required ghost values is the key to high performance of most PDE-based parallel programs. Mesh Types n Structured – DA objects n Unstructured – Vec. Scatter objects important concepts Usage Concepts n Geometric data n Data structure creation n Ghost point updates n Local numerical computation data layout 39

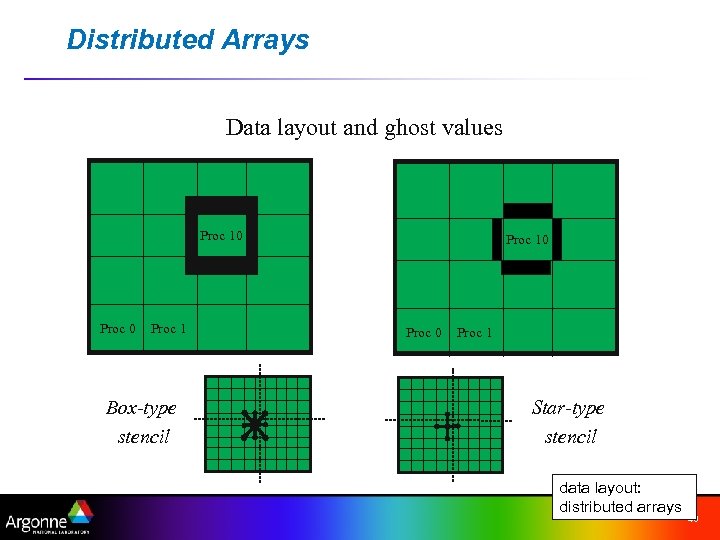
Distributed Arrays Data layout and ghost values Proc 10 Proc 1 Box-type stencil Proc 10 Proc 1 Star-type stencil data layout: distributed arrays 40

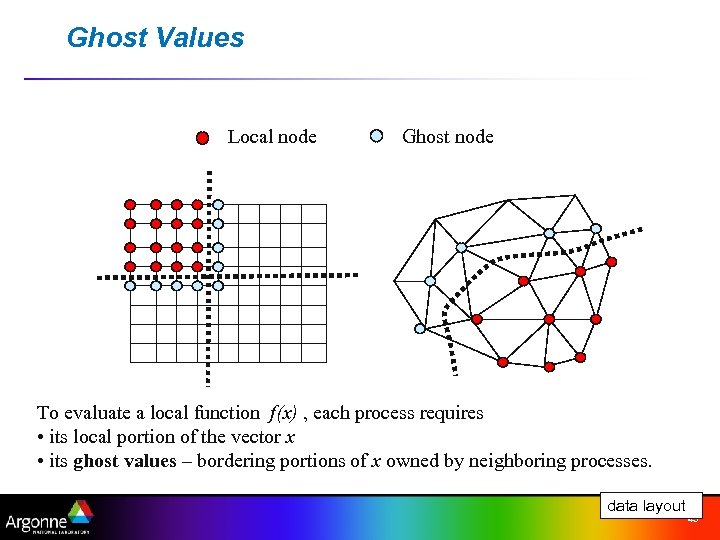
Ghost Values Local node Ghost node To evaluate a local function f(x) , each process requires • its local portion of the vector x • its ghost values – bordering portions of x owned by neighboring processes. data layout 43

Communication and Physical Discretization Communication Geometric Data stencil [implicit] Data Structure Ghost Point Creation Data Structures DACreate( ) DA AO Ghost Point Updates DAGlobal. To. Local( ) structured meshes elements edges vertices Vec. Scatter. Create( ) AO Loops over I, J, K indices 1 Vec. Scatter( ) unstructured meshes Local Numerical Computation Loops over entities 2 data layout 44

Framework for Multi-model Algebraic System ~petsc/src/snes/examples/tutorials/ex 31. c, ex 32. c http: //www-unix. mcs. anl. gov/petscas/snapshots/petscdev/tutorials/multiphysics/tutorial. html 51

How Can We Help? n Provide documentation: – http: //www. mcs. anl. gov/petsc n Quickly answer questions n Help install n Guide large scale flexible code development n Answer email at petsc-maint@mcs. anl. gov 58