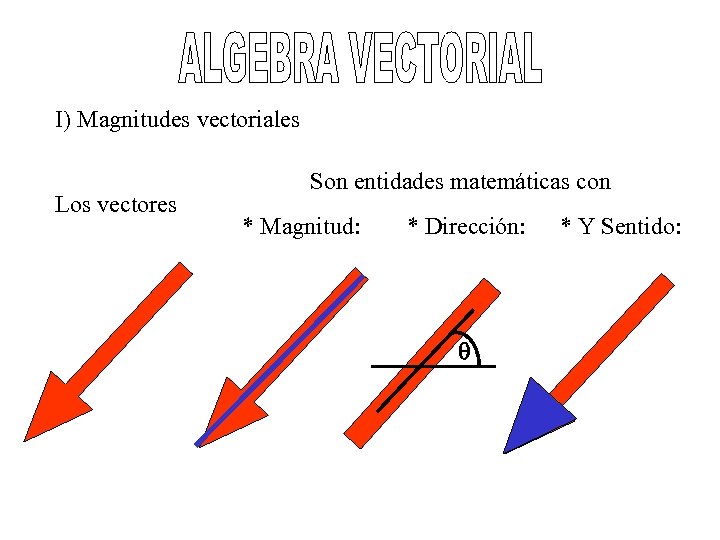
I Magnitudes vectoriales Los vectores Son entidades matemáticas

I) Magnitudes vectoriales Los vectores Son entidades matemáticas con * Magnitud: * Dirección: q * Y Sentido:

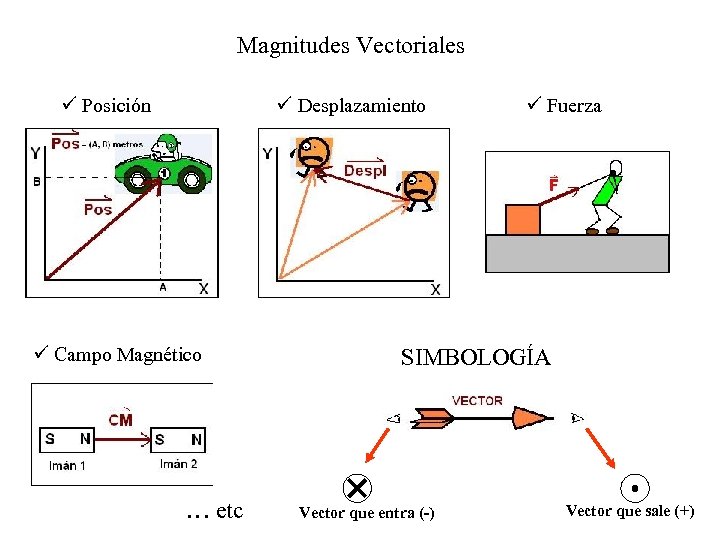Magnitudes Vectoriales ü Posición ü Desplazamiento ü Campo Magnético … etc ü Fuerza SIMBOLOGÍA Vector que entra (-) Vector que sale (+)

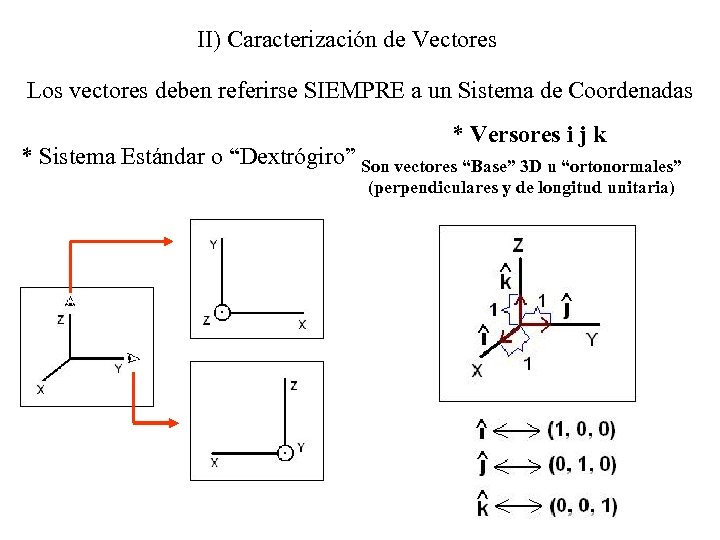II) Caracterización de Vectores Los vectores deben referirse SIEMPRE a un Sistema de Coordenadas * Versores i j k * Sistema Estándar o “Dextrógiro” Son vectores “Base” 3 D u “ortonormales” (perpendiculares y de longitud unitaria)

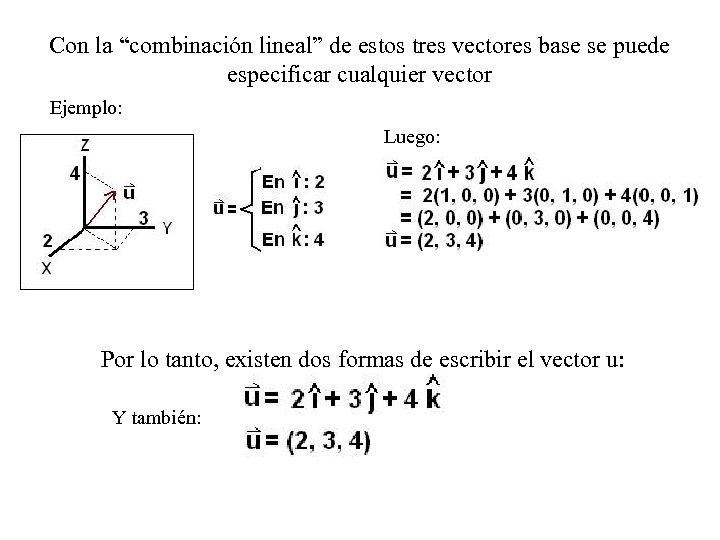Con la “combinación lineal” de estos tres vectores base se puede especificar cualquier vector Ejemplo: Luego: Por lo tanto, existen dos formas de escribir el vector u: Y también:

* Módulo y versor de un vector arbitrario Sea - La longitud o “módulo” de A es: - Y el versor de A es: Ejemplo: NOTA: el versor indica los “Cosenos Directores”:

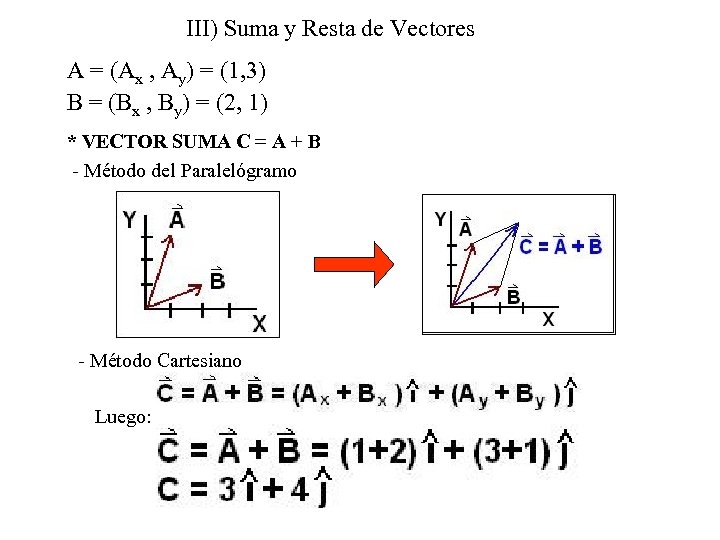III) Suma y Resta de Vectores A = (Ax , Ay) = (1, 3) B = (Bx , By) = (2, 1) * VECTOR SUMA C = A + B - Método del Paralelógramo - Método Cartesiano Luego:

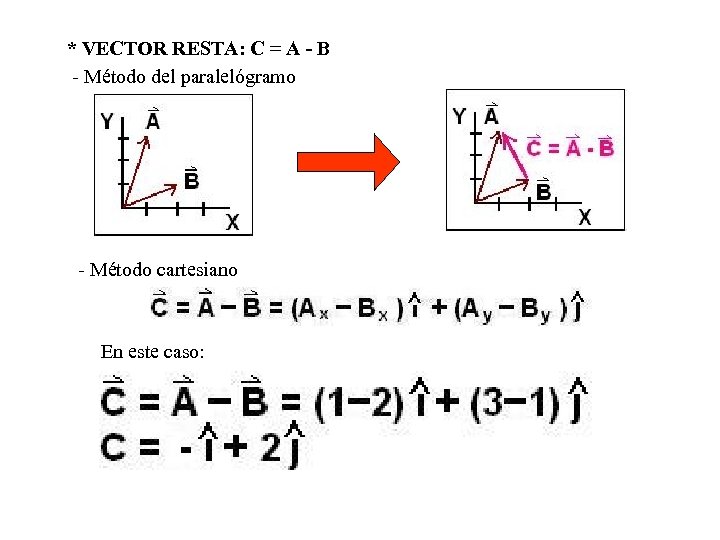* VECTOR RESTA: C = A - B - Método del paralelógramo - Método cartesiano En este caso:

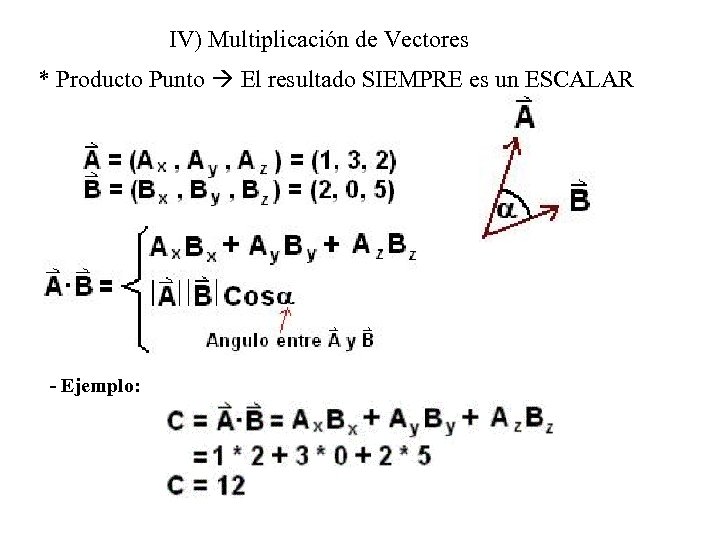IV) Multiplicación de Vectores * Producto Punto El resultado SIEMPRE es un ESCALAR - Ejemplo:

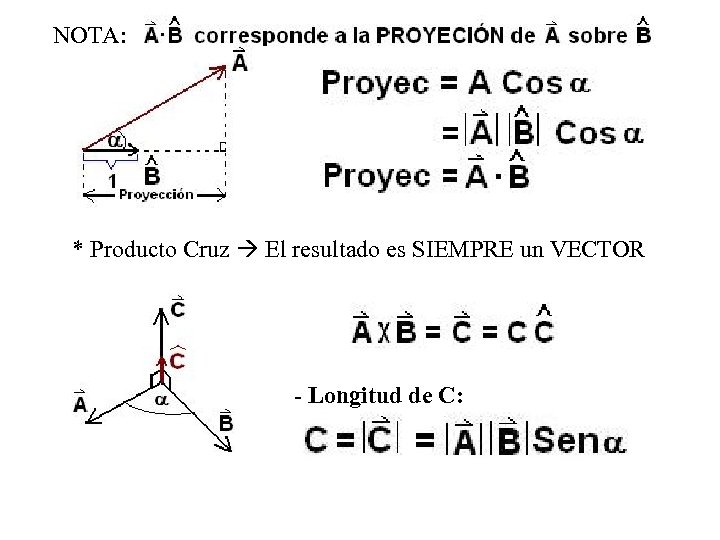NOTA: * Producto Cruz El resultado es SIEMPRE un VECTOR - Longitud de C:

Finalmente:

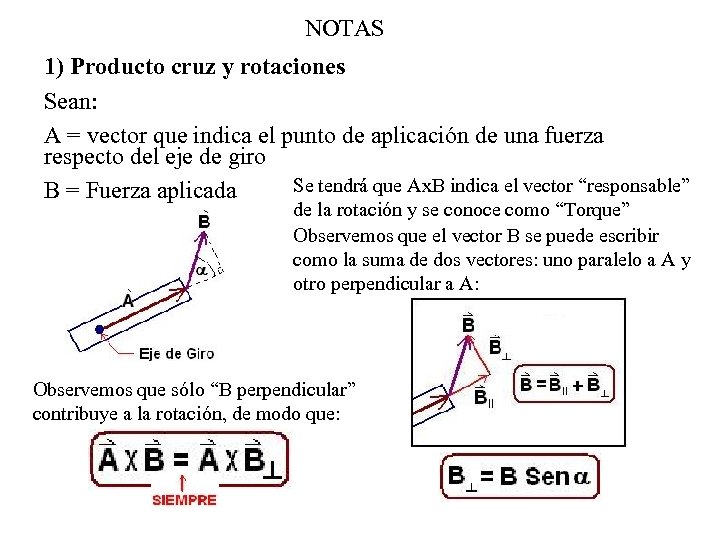NOTAS 1) Producto cruz y rotaciones Sean: A = vector que indica el punto de aplicación de una fuerza respecto del eje de giro Se tendrá que Ax. B indica el vector “responsable” B = Fuerza aplicada de la rotación y se conoce como “Torque” Observemos que el vector B se puede escribir como la suma de dos vectores: uno paralelo a A y otro perpendicular a A: Observemos que sólo “B perpendicular” contribuye a la rotación, de modo que:

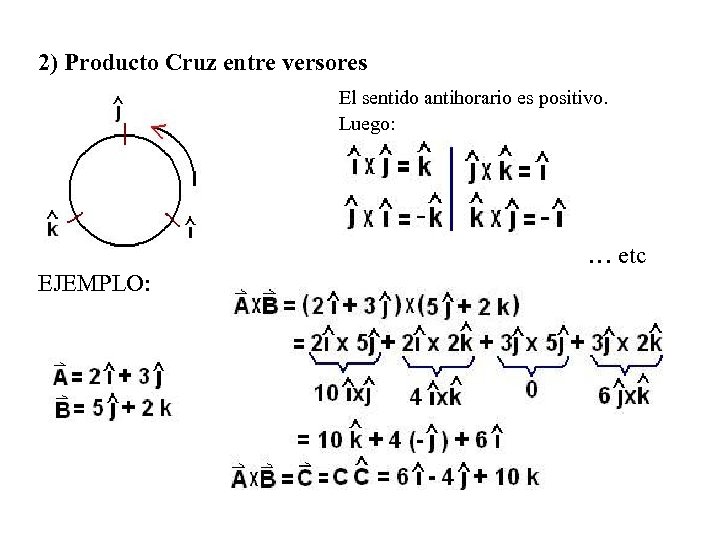2) Producto Cruz entre versores El sentido antihorario es positivo. Luego: … etc EJEMPLO:

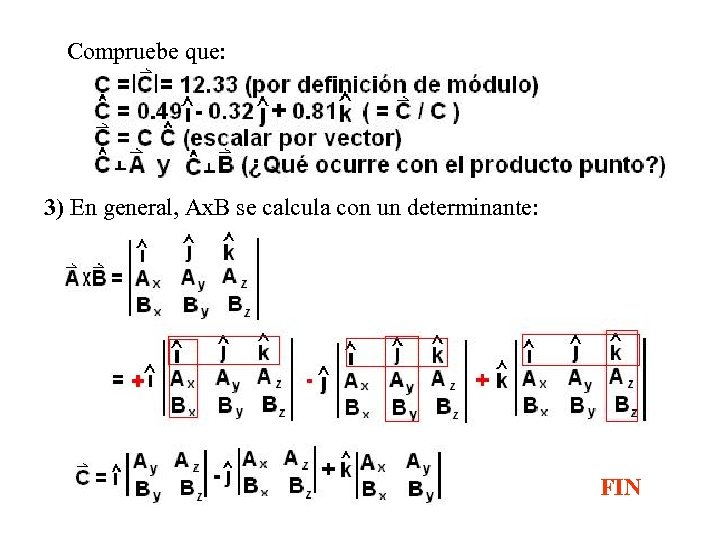Compruebe que: 3) En general, Ax. B se calcula con un determinante: FIN