I m not paying that Mathematical models for setting

I’m not paying that! Mathematical models for setting air fares

Contents • Background – History – What’s the problem? • Solving the basic problem • Making the model more realistic • Conclusion • Finding out more

Air Travel in the Good Old Days Only the privileged few – 6000 passengers in the USA in 1926

And now … Anyone can go – easy. Jet carried 30. 5 million passengers in 2005

What’s the problem? • Different people will pay different amounts for an airline ticket – Business people want flexibility – Rich people want comfort – The rest of us just want to get somewhere • You can sell seats for more money close to departure

Make them pay! • Charge the same price for every seat and you miss out on money or people – Too high: only the rich people or the business people will buy – Too low: airline misses out on the extra cash that rich people might have paid £ 30 I fancy a holiday I’ve got a meeting on 2 nd June £ 100

Clever Pricing • Clever pricing will make the airline more money – What fares to offer and when – How many seats to sell at each fare • Most airlines have a team of analysts working full time on setting fares • Turnover for easy. Jet in 2007 was £ 1. 8 billion so a few percent makes lots of money!

Contents • Background • Solving the basic problem – It’s your turn – Linear programming • Making the model more realistic • Conclusion • Finding out more

It’s your turn! • Imagine that you are in charge of selling tickets on the London to Edinburgh flight • How many tickets should you allocate to economy passengers? § Capacity of plane = 100 seats § 150 people want to buy economy seats § 50 people want to buy business class seats § Economy tickets cost £ 50 § Business class tickets cost £ 200

3 volunteers needed No hard sums!

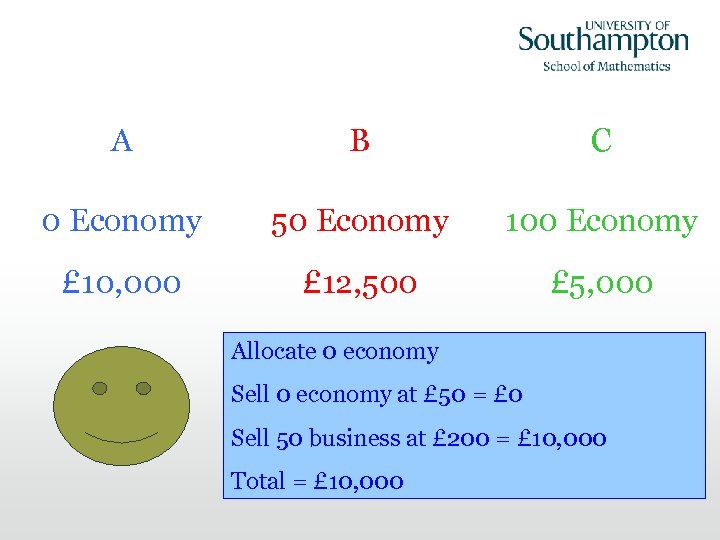A B C 0 Economy 50 Economy 100 Economy £ 10, 000 £ 12, 500 £ 5, 000 Allocate 50 economy 100 economy Sell 50 economy at £ 50 == £ 5, 000 0 economy at £ 50 = £ 2, 500 100 economy at £ 50 £ 0 Sell 50 business at £ 200 = £ 10, 000 0 business at £ 200 = £ 0 Total = £ 12, 500 £ 10, 000 £ 5, 000

Using equations • Assume our airline can charge one of two prices – HIGH price (business class) pb – LOW price (economy class) pe • Assume demand is deterministic – We can predict exactly what the demand is for business class db and economy class de • How many seats should we allocate to economy class to maximise revenue? • Write the problem as a set of linear equations

Revenue • We allow xe people to buy economy tickets and xb to buy business class tickets • Therefore, revenue on the flight is * Maximise * Economy revenue Business revenue

Constraints • Constraint 1: the aeroplane has a limited capacity, C • i. e. the total number of seats sold must be less than the capacity of the aircraft • Constraint 2: we can only sell positive numbers of seats

More Constraints • Constraint 3: we cannot sell more seats than people want • Constraint 4: the number of seats sold is an integer

In Numbers … • We allow xe people to buy economy tickets and xb to buy business class tickets • Therefore, revenue on the flight is * Maximise * Economy revenue Business revenue

And Constraints … • Constraint 1: aeroplane has limited capacity, C • Constraint 2: sell positive numbers of seats • Constraint 3: can’t sell more seats than demand

Linear Programming • We call xe and xb our decision variables, because these are the two variables we can influence • We call R our objective function, which we are trying to maximise subject to the constraints • Our constraints and our objective function are all linear equations, and so we can use a technique called linear programming to solve the problem

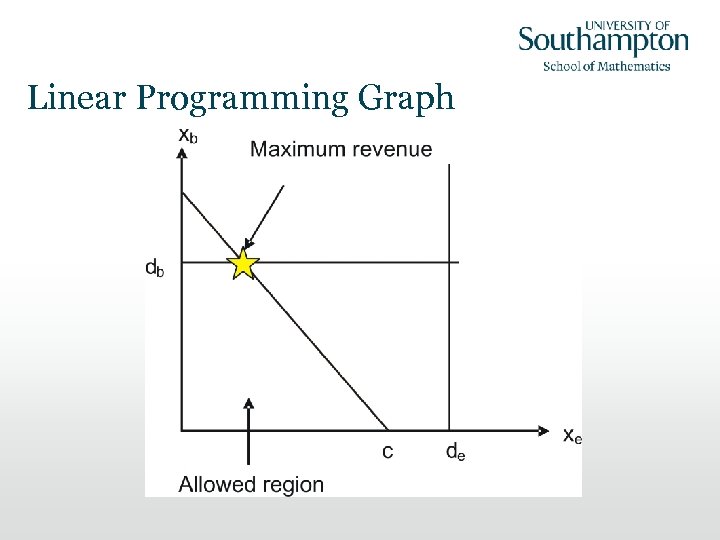Linear Programming Graph

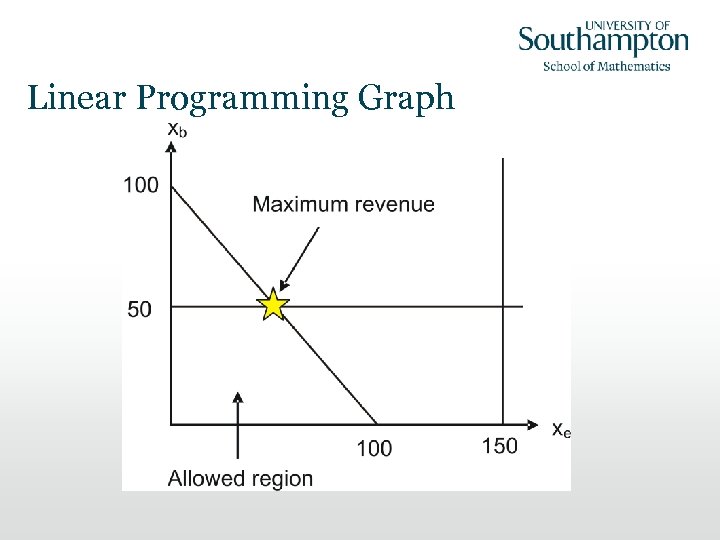Linear Programming Graph

Solution • Fill as many seats as possible with business class passengers • Fill up the remaining seats with economy passengers xb = db, xe = C – xb for db < C xb = C for db > C 50 economy, 50 business (Option B)

But isn’t this easy? • If we know exactly how many people will want to book seats at each price, we can solve it – This is the deterministic case – In reality demand is random • We assumed that demands for the different fares were independent – Some passengers might not care how they fly or how much they pay • We ignored time – The amount people will pay varies with time to departure

Contents • Background • Solving the basic problem • Making the model more realistic – Modelling customers – Optimising the price • Conclusion • Finding out more

Making the model more realistic: • We don’t know exactly what the demand for seats is - Use a probability distribution for demand • Price paid depends only on time left until departure or number of bookings made so far – Price increases as approach departure – Fares are higher on busy flights • Model buying behaviour, then find optimal prices

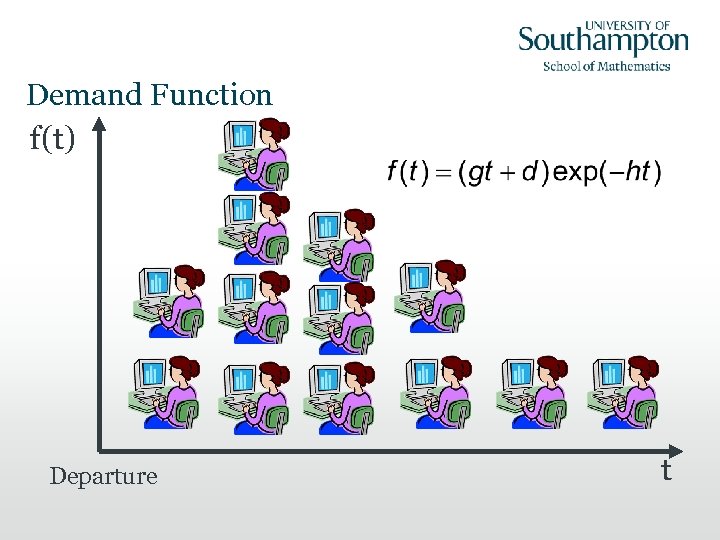Demand Function f(t) Departure e. g. t

Reserve Prices • Each customer has a reserve price for the ticket – Maximum amount they are prepared to pay • The population has a distribution of reserve prices y(t), written as p(t, y(t)) – Depends on time to departure t

Reserve Prices £ 30 I’d like to buy a ticket to Madrid on 2 nd June March 2008 I’ve got a meeting in Madrid on 2 nd June – I’d better buy a ticket £ 10 0

Reserve Prices £ 70 All my friends have booked – I need this ticket May 2008 The meeting’s only a week away – I’d better buy a ticket £ 200

Revenue * Maximise * Revenue = Price charged at time t Number who consider buying Proportion who buy if price is less than or equal to y(t)

Maximising Revenue • Aim: Maximise revenue over the whole selling period, without overfilling the aircraft • Decision variable: price function, y(t) • Use calculus of variations to find the optimal functional form for y(t) • Take account of the capacity constraint by using Lagrangian multipliers

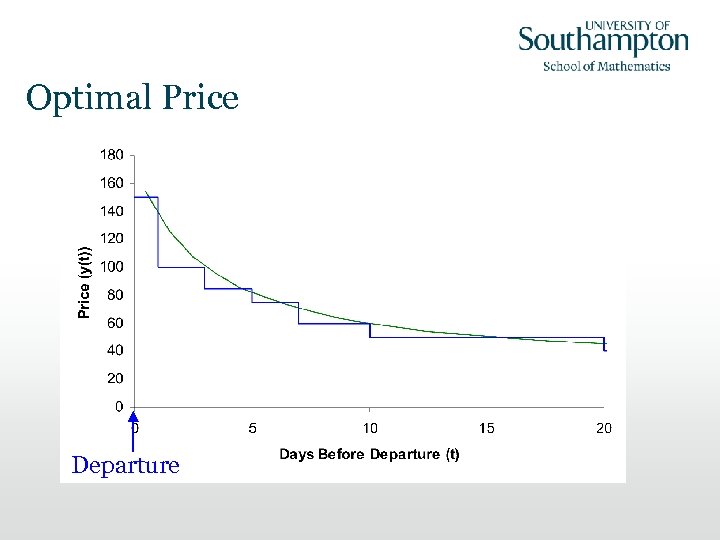Optimal Price Departure

Contents • Background • Solving the basic problem • Making the problem more realistic • Conclusion – Why just aeroplanes? • Finding out more

Why Just Aeroplanes? • Many industries face the same problem as airlines – Hotels – maximise revenue from a fixed number of rooms: no revenue if a room is not being used – Cinemas – maximise revenue from a fixed number of seats: no revenue from an empty seat – Easter eggs – maximise revenue from a fixed number of eggs: limited profit after Easter

Is this OR? • OR = Operational Research, the science of better – Using mathematics to model and optimise real world systems Yes!

Is this OR? • OR = Operational Research, the science of better – Using mathematics to model and optimise real world systems • Other examples of OR – Investigating strategies for treating tuberculosis and HIV in Africa – Reducing waiting lists in the NHS – Optimising the set up of a Formula 1 car – Improving the efficiency of the Tube!

Contents • Background • Solving the basic problem • Making the problem more realistic • Conclusion

How to Get a Good Deal fi ro P 02 Book early on £ 2 an = 07 unpopular flight 20 in et y. J as e or f t i m on lli

Questions?