и д ю ь л т к а а т К и ч с ау н и ч и л ь с
Учиться считать люди начали в незапамятные времена, а учителем у них была сама жизнь.
Древние люди добывали себе пищу главным образом охотой. На крупного зверя – бизона или лося – приходилось охотиться всем племенем: в одиночку ведь с ним не справишься. Командовал облавой обычно самый старый и опытный охотник. Чтобы добыча не ушла, ее надо было окружить, ну вот хотя бы так: пять человек справа, семь сзади, четыре слева. Тут уж без счета никак не обойдешься! И вождь первобытного племени справлялся с этой задачей. Даже в те времена, когда человек не знал таких слов, как “пять” или “семь”, он мог показать числа на пальцах рук.
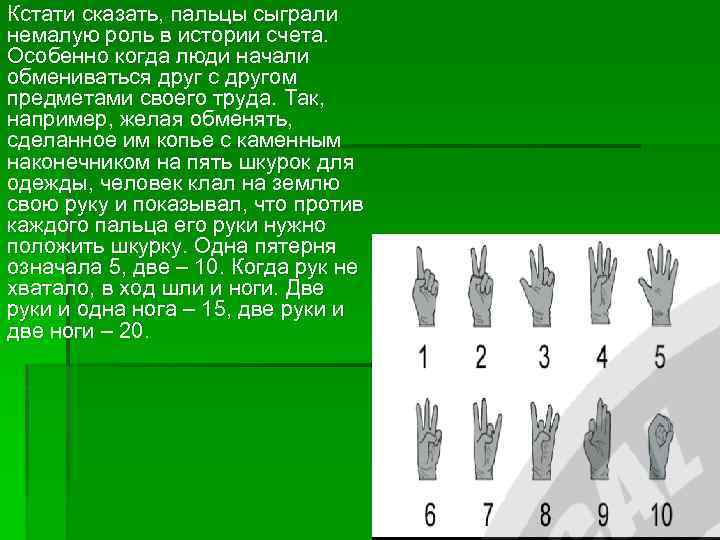Кстати сказать, пальцы сыграли немалую роль в истории счета. Особенно когда люди начали обмениваться друг с другом предметами своего труда. Так, например, желая обменять, сделанное им копье с каменным наконечником на пять шкурок для одежды, человек клал на землю свою руку и показывал, что против каждого пальца его руки нужно положить шкурку. Одна пятерня означала 5, две – 10. Когда рук не хватало, в ход шли и ноги. Две руки и одна нога – 15, две руки и две ноги – 20.
§ В пятерке можно узнать кулак с отставленным пальцем, даже само слово “пять” происходит от слова “пясть” – кисть руки.
Пальцы были первыми изображениями чисел. Очень сложно было складывать и вычитать. Загибаешь пальцы – складываешь, разгибаешь – вычитаешь. Когда люди еще не знали, что такое цифры, в ход при счете шли и камешки, и палочки. В старину, если крестьянин-бедняк брал в долг у богатого соседа несколько мешков зерна, он выдавал вместо расписки палочку с зарубками – бирку. На палочке делали столько зарубок, сколько было взято мешков. Эту палочку раскалывали: одну половинку должник отдавал богатому соседу, а другую оставлял себе, чтобы тот потом не требовал вместо трех мешков пять. Если давали деньги другу в долг, тоже отмечали это на палочке. Словом, в старину бирка служила чем-то вроде записной книжки.
Как люди научились записывать цифры
§ Проходили многие-многие годы. Менялась жизнь человека. Люди приручили животных, на земле появились первые скотоводы, а затем и земледельцы. Постепенно росли знания людей, и чем дальше, тем больше увеличивалась потребность в умении считать и мерить. Скотоводам приходилось пересчитывать свои стада, а при этом счет мог идти уже сотнями и тысячами. Земледельцу надо было знать, сколько земли засеять, чтобы прокормить себя до следующего урожая. А время посева? Ведь, если посеять не во время, урожая не получишь!
Счет времени по лунным месяцам уже не годился. Нужен был точный календарь. К тому же людям все чаще приходилось сталкиваться с большими числами, запомнить которые трудно или даже невозможно. Нужно было придумать, как их записывать.
§ У древних греков, например, вместо цифр, были буквы. Буквами обозначались цифры и в древних русских книгах: “А” - это один, “Б” - два, “В” – три и т. д.
§ в разных странах и в разные времена это делалось поразному. Очень разные и порою даже забавные эти “цифры” у разных народов. В Древнем Египте числа первого десятка записывали соответствующим количеством палочек. Вместо цифры “ 3” – три палочки. А вот для десятков уже другой знак – вроде подковы.
§ У древних римлян были другие цифры. Мы и сейчас пользуемся иногда римскими цифрами. Их можно увидеть и на циферблате часов, и в книге, где обозначается номер главы. Если внимательно рассмотреть, римские цифры похожи на пальцы. Один – это один палец; два – два пальца; пять – это пятерня с отставленным большим пальцем; шесть – это пятерня да еще один палец.
§ Цифру “ 1” писали так же, как и сейчас, палочкой, цифру “ 2” – двумя палочками, только не стоячими, а лежачими. Когда эти две палочки быстро писали одну под другой, их соединяли косой черточкой, как мы соединяем буквы в слова. Вот и получился значок, напоминающий нашу теперешнюю двойку. Тройка получалась при скорописи из трех палочек, лежащих одна под другой
Индейцы майя ухитрялись писать любое число, используя только точку, линию и кружочек.
§ Все-таки, откуда же взялись те десять цифр, которыми мы пользуемся сегодня? Наши современные цифры пришли к нам из Индии через арабские страны, поэтому их и называют арабскими. Происхождение каждой из девяти арабских цифр хорошо видно, если их записать в “угловатой” форме. . От арабов к нам пришло и слово “цифра” от слова “сифр”. Цифрами называют все десять значков для записи чисел, которыми мы пользуемся: 0, 1, 2, 3, 4, 5, …….
§ А что насчет нуля? ? ?
Современное слово “нуль” появилось гораздо позже, чем “цифра”. Оно происходит от латинского слово “нулла” – “никакая”. Изобретение нуля считается одним из важнейших математических открытий. При новом способе записи чисел значение каждой написанной цифры стало прямо зависеть от нее.
Загадка чисел Фибоначчи
Содержание: § § § Краткая биография Фибоначчи Волшебные числа Прямоугольник Фибоначчи Числа Фибоначчи в нашей жизни Спирали Фибоначчи в природе
Кто такой Фибоначчи? Леонардо Фибоначчи — итальянский математик (1180 -1240). Родился в Пизе. Его алгебра — одна из первых появившихся в Европе. Он долгое время жил на Востоке, где и познакомился с математикой арабов, в том числе, с алгеброй Мохаммеда бен-Музы, который, в свою очередь, почерпал свои знания из индийской математической литературы и более всего из сочинений Брахмагупты. Леонардо находил уже связь между алгеброй и геометрией.
Волшебные числа Знаменитый ряд чисел Фибоначчи образует изначальный принцип золотого отношения. Этот ряд образован постоянным сложением предыдущих двух чисел, что выражается в следующем бесконечном численном ряду : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …и так далее. Соотношение между всеми этими числами приблизительно равно золотому сечению.
Прямоугольник Фибоначчи Прямоугольник с шириной и высотой, равными двум соседним числам последовательности, представляет собой так называемый "Золотой прямоугольник", идеальный прямоугольник. Золотой прямоугольник можно разбить на более мелкие, с размерами, соответствующими соседним числам Фибоначчи. Если мы возьмем этот золотой прямоугольник и разобьем его на более мелкие в соответствии с последовательностью Фибоначчи и разделим каждый из них система начнет приобретать некую форму - мы увидим так называемую "Спираль Фибоначчи".
Числа Фибоначчи делят нашу жизнь на количество прожитых лет:
1 – ый год Ребенок овладел ходьбой и осваивает ближайшее окружение , познаёт мир руками.
2 год Понимает речь и действует, пользуясь словесными указаниями , открытие себя.
3 года Действует посредством слова, задает вопросы.
5 лет Гармония психомоторики, памяти, воображения и чувства, которые уже позволяют ребенку охватить мир во всей его целостности.
8 лет На передний план выходит чувство воображение.
13 лет Начинает работать механизм таланта.
21 год Механизм творчества приблизился к состоянию гармонии и делаются попытки выполнять талантливую работу.
34 год Гармония мышления, чувств, воображения и психомоторики: рождается способность к гениальной работе.
55 лет В этом возрасте, при условии сохраненной гармонии души и тела, человек готов стать творцом.
Спирали Фибоначчи в природе
Спирали Фибоначчи в природе Смерч тоже приобретает спиралевидную форму.
Спирали Фибоначчи в природе Примером может быть и тысячелистник. Складывая его старые и новые ветви можно увидеть последовательност ь Фибоначчи.
Спирали Фибоначчи в природе Если пересчитать лепестки некоторых наиболее распространенных цветов, - например, ириса с его 3 лепестками, первоцвета с 5 лепестками, крестовника с 13 лепестками, маргаритки с 34 лепестками и астры с 55 (и 89) лепестками, то и тут видна последовательность
Спирали Фибоначчи в природе Ураган тоже закручивается спиралью.
Спирали Фибоначчи в природе Если приглядеться то можно увидеть что паук плетёт спиралевидную паутину.
Спирали Фибоначчи в природе Оказывается спираль Фибоначчи есть и на отпечатке пальца.
Спирали Фибоначчи в природе Спираль есть и на цветах.
Спирали Фибоначчи в природе Спираль Фибоначчи можно увидеть даже в самых обычных морских раковинах.
Спирали Фибоначчи в природе Пирамиды. В отличие от других египетских пирамид это не гробница, а скоpее неразрешимая головоломка из числовых комбинаций. Мастерство и труд и изобретательность использованные архитекторами при возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Kлюч к геометроматематическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.
Спирали Фибоначчи в природе Но самый потрясающий пример находится прямо над нашей головой на расстоянии приблизительно в 100 000 световых лет - даже спирали галактик сформированы по абсолютно тому же принципу, как и та крошечная раковина. . .
Используемые интернет-ресурсы: http: //festival. 1 septem ber. ru/articles/573140/ http: //shkolazhizni. ru/a rchive/0/n-24807/ http: //www. google. ru/