i-4 security Security taxonomy Physical security

i-4 security

Security taxonomy • Physical security • Resource exhaustion • Key-based security • cryptography

Security dichotomy • Computer (system) Security – automated tools and mechanisms to protect data in a computer, even if the computers are connected to a network • against hackers (intrusion) • against viruses • against Denial of Service attacks – Access control, authorization, … • Internet (network) Security – measures to prevent, detect, and correct security violations that involve the transmission of information in a network or interconnected network – Everything on the network can be a target – Every transmitted bit can be tapped

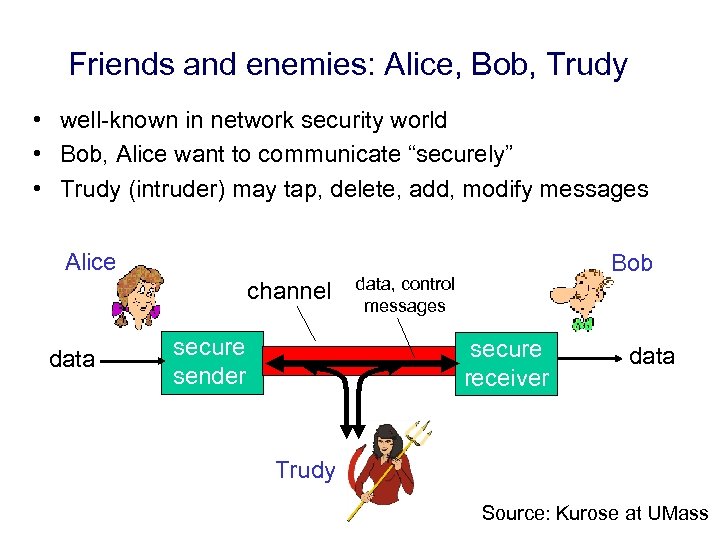Friends and enemies: Alice, Bob, Trudy • well-known in network security world • Bob, Alice want to communicate “securely” • Trudy (intruder) may tap, delete, add, modify messages Alice channel data secure sender Bob data, control messages secure receiver data Trudy Source: Kurose at UMass

There are bad guys (and girls) out there! Q: What can a “bad guy” do? A: A lot! – eavesdrop: intercept messages – Insert/modify/delete messages into connection – impersonation: can fake (spoof) source address in packet (or any field in packet) – hijacking: “take over” ongoing connection by removing sender or receiver, inserting himself in place – denial of service: prevent service from being used by others (e. g. , by overloading resources) Source: Kurose at UMass

Thwart the attacks! • Basic Security services – authentication • Access control – confidentiality – Data (or message) integrity – Non-repudiation

More Security services • • • Anonymity Availability Accountability Privacy forensics

Security mechanisms • Encipherment – Encryption and decryption – Keys • Message digest – Hash function characteristics • it is easy to compute the hashed value for any given message, • it is infeasible to find a message that has a given hash, • it is infeasible to find two different messages with the same hash – Can have a key (Cryptographic) • Digital Signatures – demonstrating the authenticity of a digital message or document

Meaning of Cryptography • from Greek – Cryptos: secret, hidden – graphos: writing – cryptography: study of secret writing

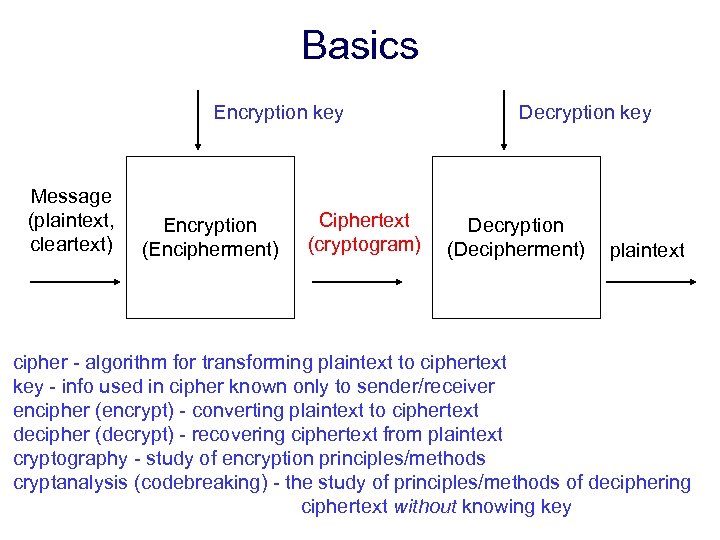Basics Encryption key Message (plaintext, cleartext) Encryption (Encipherment) Ciphertext (cryptogram) Decryption key Decryption (Decipherment) plaintext cipher - algorithm for transforming plaintext to ciphertext key - info used in cipher known only to sender/receiver encipher (encrypt) - converting plaintext to ciphertext decipher (decrypt) - recovering ciphertext from plaintext cryptography - study of encryption principles/methods cryptanalysis (codebreaking) - the study of principles/methods of deciphering ciphertext without knowing key

Classification of Cryptosystems • The way in which keys are used – Symmetric cryptography • Single key – Public key cryptography • Two keys • the way in which plaintext is processed – Block cipher – Stream cipher

Symmetric cryptography

Symmetric Encryption • also known as – – Classical, conventional private-key single-key Secret key • sender and recipient share a common key • was only type prior to invention of public-key cryptography – until second half of 1970’s

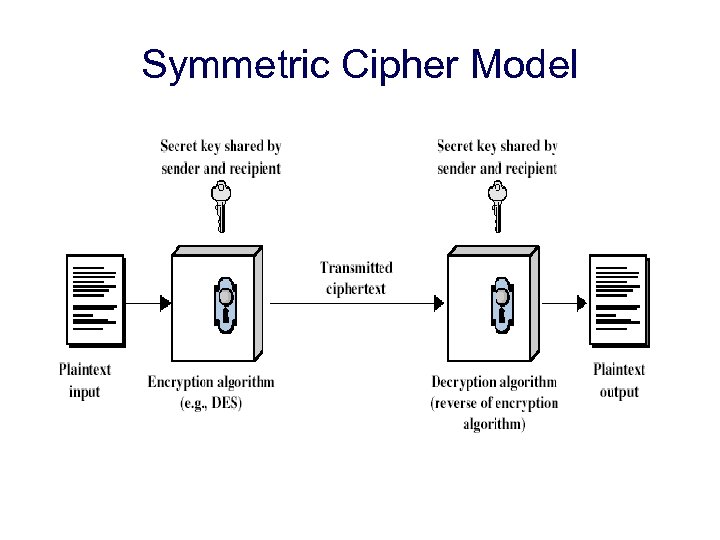Symmetric Cipher Model there must be a secure mechanism for the distribution of this key a priori

Requirements • two requirements for secure use of symmetric encryption: – a strong encryption algorithm – a secret key known only to sender / receiver Y = EK(X) X = DK(Y) • assume encryption algorithm is known • imply a secure channel to distribute the key

X-or( ) in cryptography • • Sender wants to send M to receiver M (Original plaintext): 1010 K (Key): 0011 M K = 1001 (Encrypted ciphertext) 1001 transmitted • Receiver already knows K • (M K) K= 1001 0011 = 1010 = M -> original message is restored!

Some primitives • Substitution • Permutation

Two types of symmetric ciphers • Stream cipher – Encrypts one bit at a time – RC 4 • Block cipher – Encrypts a block of bits at a time – DES, AES

Asymmetric cryptography Or Public key cryptography (PKC)

PKC – General Characteristics • public-key/two-key/asymmetric cryptography • uses 2 keys – public-key • may be known by anybody, and can be used to encrypt messages, and verify signatures – private-key • known only to the recipient, used to decrypt messages, and sign (create) signatures • keys are related to each other but it is not feasible to find out private key from the public one – Modular arithmetic

PKC – General Characteristics • It is computationally easy to en/decrypt messages when the relevant keys are known – • RSA Trap-door one-way function – ku: public-key, kr: private key Y=fku(X) easy, if ku and X are known X=fkr-1(Y)easy, if kr and Y are known, but infeasible if Y is known but kr is not known

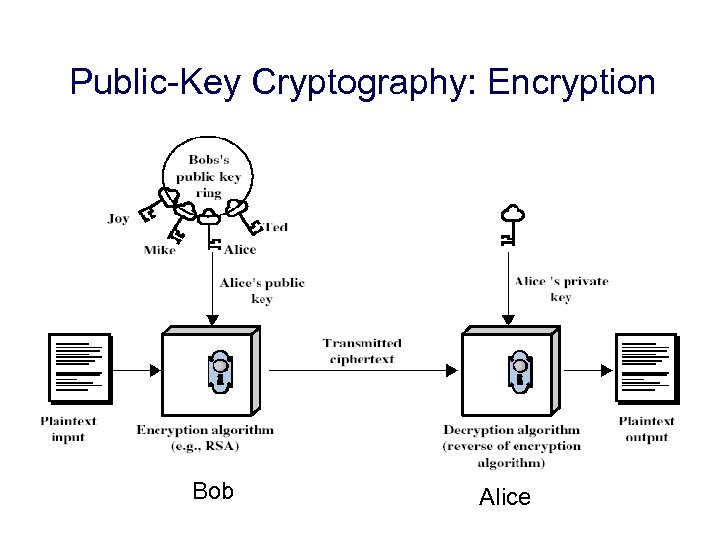Public-Key Cryptography: Encryption Bob Alice

Another notation • Alice has a public key, kp, and a secret key, ks • Alice’s public key is known to Bob • Asymmetric Cipher: F-1(F(m, kp), ks) = m Bob Alice 1. Construct m 2. Compute c= F(m, kp) 3. Send c to Bob c 4. Receive c from Alice 5. Compute d=F-1(c, ks) 6. m = d

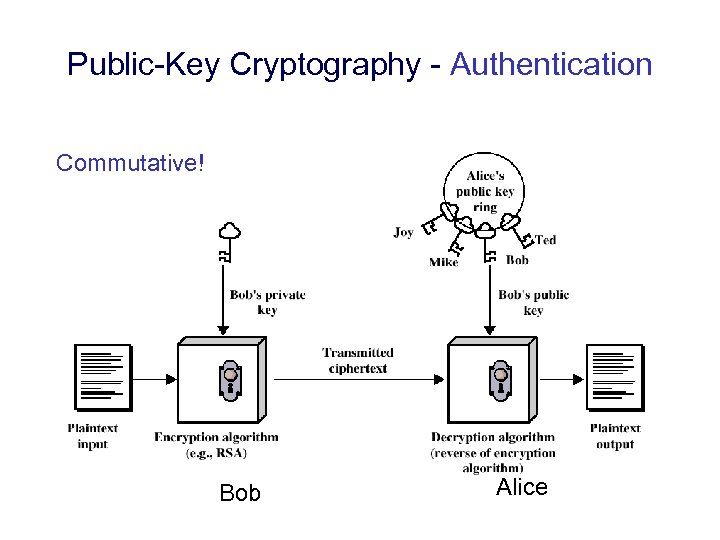Public-Key Cryptography - Authentication Commutative! Bob Alice

Why PKC? • Initially developed to address two challenging issues: – key distribution • symmetric crypto requires how to securely share the key • in PKI you do not need to distribute/know secret keys, but you need trusted third parties – digital signatures (non-repudiation) • not possible with symmetric crypto

Diffie-Hellman (D-H) Algorithm • D-H model’s primary contribution: – Take a prime p and a primitive element g • Cyclic group in finite field – – Publicize both g and p Alice chooses some x Zp* and sends (gx mod p) to Bob chooses some y Zp* and sends (gy mod p) to Alice Eve can see both (gx mod p) and (gy mod p) but she cannot calculate x or y • Discrete logarithm problem 26

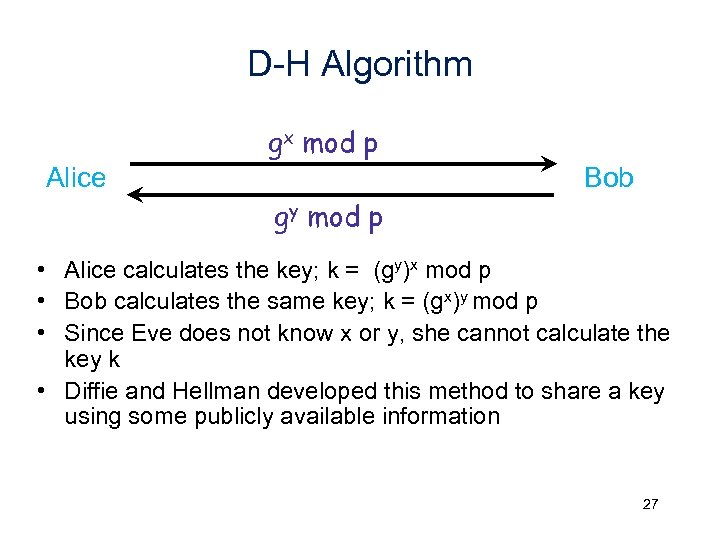D-H Algorithm gx mod p Alice Bob gy mod p • Alice calculates the key; k = (gy)x mod p • Bob calculates the same key; k = (gx)y mod p • Since Eve does not know x or y, she cannot calculate the key k • Diffie and Hellman developed this method to share a key using some publicly available information 27

PKC Applications • 3 categories – encryption/decryption • to provide secrecy – digital signatures • to provide authentication and non-repudiation – key exchange • to agree on a session key (symmetric cipher) to encrypt data packets • Why not use public/private keys?

MESSAGE INTEGRITY

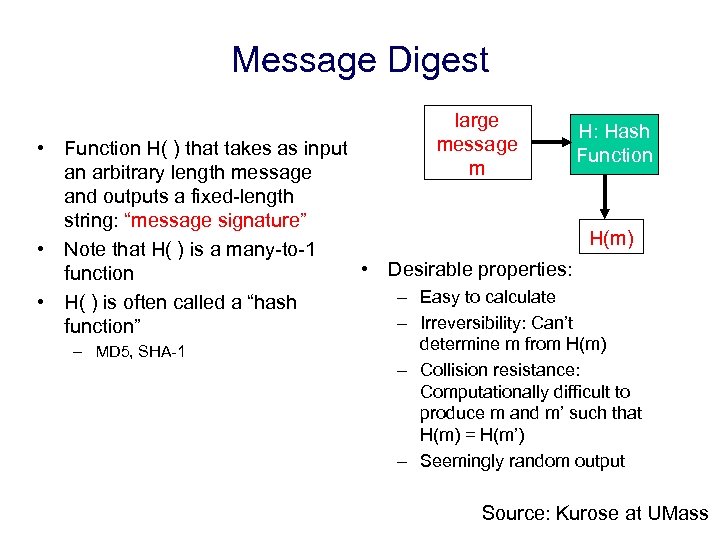Message Digest large message m H: Hash Function • Function H( ) that takes as input an arbitrary length message and outputs a fixed-length string: “message signature” H(m) • Note that H( ) is a many-to-1 • Desirable properties: function – Easy to calculate • H( ) is often called a “hash – Irreversibility: Can’t function” – MD 5, SHA-1 determine m from H(m) – Collision resistance: Computationally difficult to produce m and m’ such that H(m) = H(m’) – Seemingly random output Source: Kurose at UMass

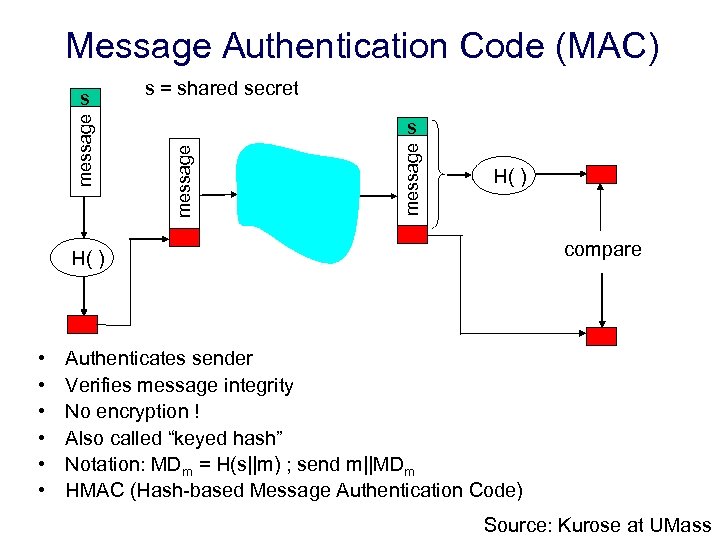Message Authentication Code (MAC) s = shared secret message s H( ) compare H( ) • • • Authenticates sender Verifies message integrity No encryption ! Also called “keyed hash” Notation: MDm = H(s||m) ; send m||MDm HMAC (Hash-based Message Authentication Code) Source: Kurose at UMass

Digital Signatures • data integrity, non-repudiation, authentication • Basic idea – use private key on the message to generate a piece of information that can be generated only by yourself • because you are the only person who knows your private key – public key can be used to verify the signature • so everybody can verify • Generally signatures are created and verified over the hash of the message – Not over the original message. Why?

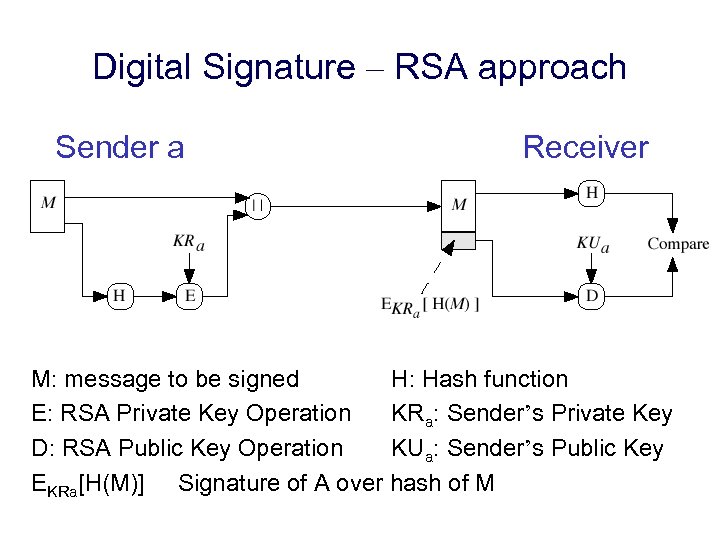Digital Signature – RSA approach Sender a Receiver M: message to be signed H: Hash function E: RSA Private Key Operation KRa: Sender’s Private Key D: RSA Public Key Operation KUa: Sender’s Public Key EKRa[H(M)] Signature of A over hash of M