http connect ustu ru ФИЗИКА Часть 1 Механика

http: //connect. ustu. ru ФИЗИКА. Часть 1. Механика. Молекулярная физика и термодинамика. Электромагнетизм. Адрес электронной образовательной среды, системы электронного обучения Гиперметод learn. urfu. ru Лектор: Карицкая Светлана Геннадьевна, Кандидат технических наук, доцент

Литература: 1. Овчинников В. А. Общая физика. Ч. ч. 1, 2. /Уч. пос. – Свердловск, 1975. 2. Трофимова Т. И. Курс физики. 11 е изд. , стер. м. : 2006. — 560 с. Учебное пособие 3. Иродов И. Е. Основные законы электромагнетизма / Уч. пос. – М. , 1991. 4. Волькенштейн. Сборник задач по общему курсу физики 5. Чертов А. Г. , Воробьев А. А. , Федоров М. Ф. Задачник по физике Рабочие тетради для студентов, обучающихся по дистанционной технологии: • Модуль № 1. Механика и элементы специальной теории относительности • Модуль № 2. Физические основы молекулярной физики и термодинамики • Модуль № 3. Электростатика. Постоянный ток • Модуль № 4. Электромагнетизм Адрес трудов кафедры https: //kf. info. urfu. ru/trudy_kafedry/ Требования: Еженедельно проходить тестирование по пройденной теме Вопросы задавать через Форум в дисциплине Физика. Часть 1. выполненную контрольную работу прислать преподавателю через Гиперметод с пометкой «Решение на проверку» 2

АББРЕВИАТУРА ВФВ – векторная физическая величина СФВ – скалярная физическая величина МТ – материальная точка 3

Физика – наука, изучающая наиболее общие формы движения материи. Под материей понимается объективная реальность, существующая вне и независимо от человеческого сознания. 4

РАЗДЕЛЫ ФИЗИКИ ü Механика (механическая форма движения материи) Ø Молекулярная физика и термодинамика ( Молекулярно кинетическая (тепловая) ) Ø Электромагнетизм (Электромагнитная) Ø Колебания и волны ( ) механическая и электромагнитная Ø Оптика (Электромагнитная) Ø Квантовая физика (Внутриатомная)

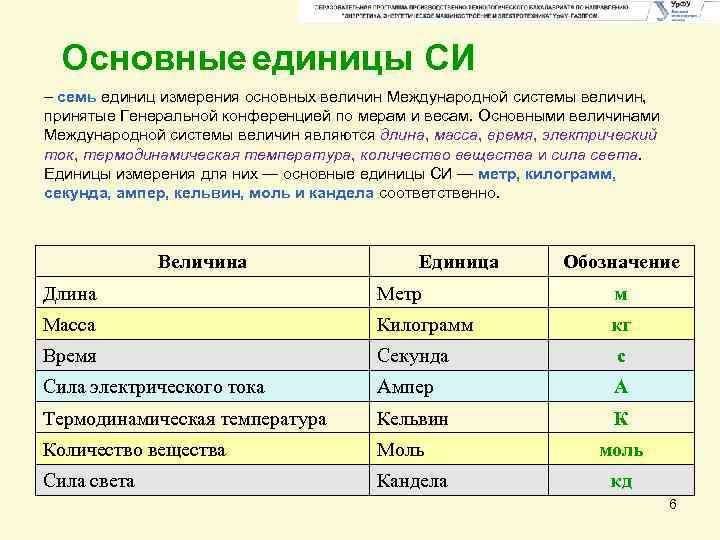Основные единицы СИ – семь единиц измерения основных величин Международной системы величин, принятые Генеральной конференцией по мерам и весам. Основными величинами Международной системы величин являются длина, масса, время, электрический ток, термодинамическая температура, количество вещества и сила света. Единицы измерения для них — основные единицы СИ — метр, килограмм, секунда, ампер, кельвин, моль и кандела соответственно. Величина Единица Обозначение Длина Метр м Масса Килограмм кг Время Секунда с Сила электрического тока Ампер А Термодинамическая температура Кельвин К Количество вещества Моль Сила света Кандела моль кд 6

Модуль 1 – МЕХАНИКА Механика часть физики, которая изучает наиболее общую форму движения материи, заключающуюся в перемещении тел или частей тела относительно друга и называемую механическим движением. Цель Рассмотреть механическое движение 1. 1 КИНЕМАТИКА 1. 2 ДИНАМИКА ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ 1. 3 СТАТИКА

Механика ПОСТУЛАТЫ КЛАССИЧЕСКОЙ МЕХАНИКИ: Ø Пространство абсолютно, т. е. расстояние между двумя его точками для всех (любых) наблюдателей одинаково и не зависит от способа его измерения; непрерывно: однородно; изотропно; евклидово; трехмерно. Оно не зависит от времени и от материи – это бесконечно протяженное, неподвижное, пустое вместилище материальных тел. Ø Время абсолютно, т. е. интервал времени между двумя событиями одинаков для всех наблюдателей и не зависит от способа его измерения непрерывно: однородно; анизотропно; течет равномерно и одинаково; одномерно. Оно существует независимо от пространства и материи. Ø Масса тела (масса – это и мера инертности, и мера количества вещества, и мера энергии, и т. д. ) абсолютна, т. е. неизменная, одинаковая (по своему численному значению) для всех наблюдателей величина, не зависящая от того, что происходит с телом, лишь бы его целостность сохранялась. 8

П. 1. ВВОДНЫЕ ПОНЯТИЯ (термины). 1. МЕХАНИЧЕСКАЯ СИСТЕМА Механической системой называется любой объект (набор объектов), механическим движением которого мы интересуемся. 9

2. МАТЕРИАЛЬНАЯ ТОЧКА (М. т. ) Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой (частицей). 10

3. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО (А. т. т. ) Тело называется абсолютно твердым, если его деформациями в условиях данной задачи можно пренебречь 11

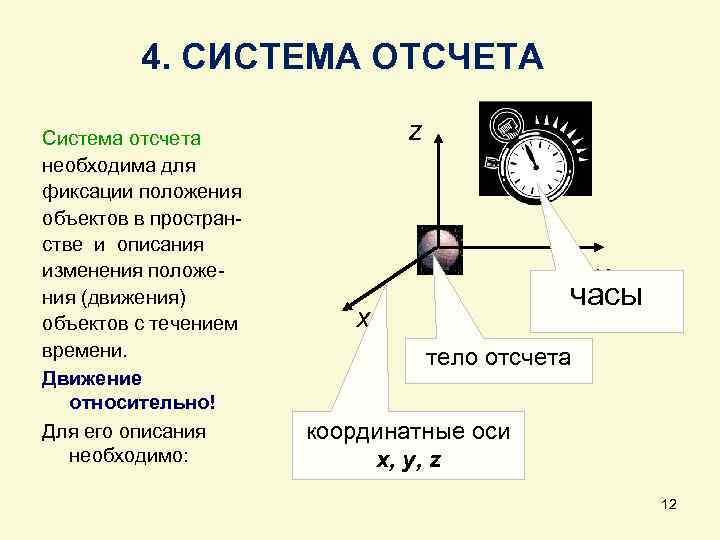4. СИСТЕМА ОТСЧЕТА Система отсчета необходима для фиксации положения объектов в простран стве и описания изменения положе ния (движения) объектов с течением времени. Движение относительно! Для его описания необходимо: z y часы x тело отсчета координатные оси x, y, z 12

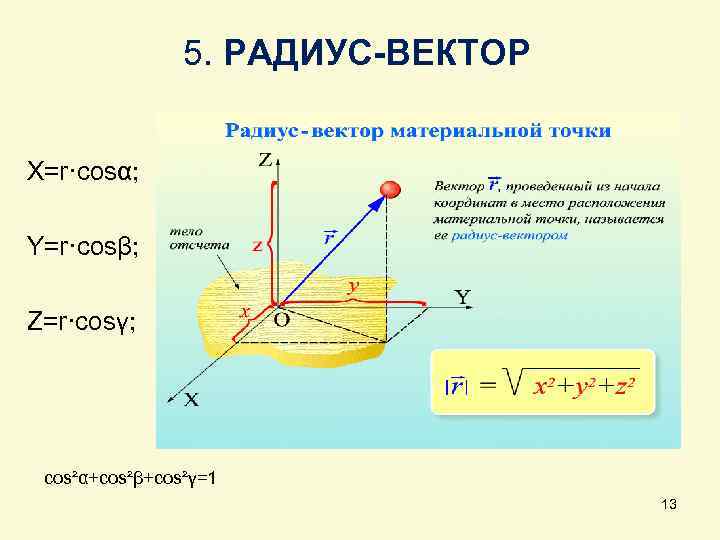5. РАДИУС-ВЕКТОР X=r·cosα; Y=r·cosβ; Z=r·cosγ; cos²α+cos²β+cos²γ=1 13

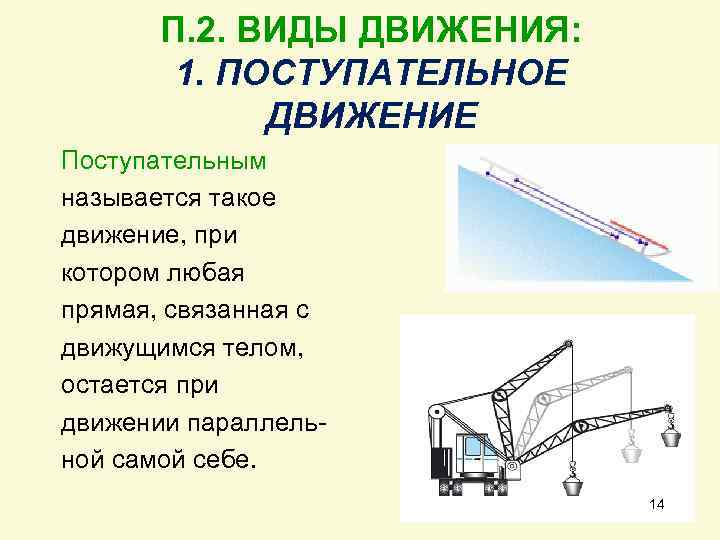П. 2. ВИДЫ ДВИЖЕНИЯ: 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ Поступательным называется такое движение, при котором любая прямая, связанная с движущимся телом, остается при движении параллель ной самой себе. 14

2. ВРАЩАТЕЛЬНОЕ Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. 15

П. 3. Траектория. Путь. www. physica. ru Траектория – вооображаемая линия, описываемая частицей при движении. Путь длина траектории. 16

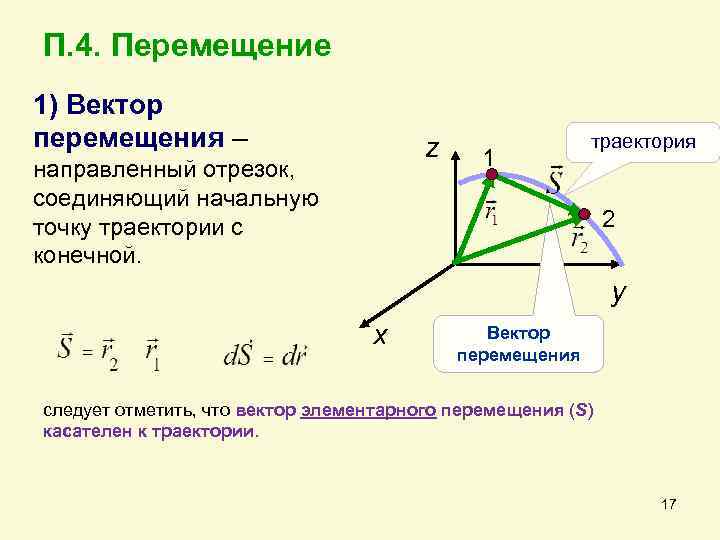П. 4. Перемещение 1) Вектор перемещения – z направленный отрезок, соединяющий начальную точку траектории с конечной. 1 траектория 2 y x Вектор перемещения следует отметить, что вектор элементарного перемещения (S) касателен к траектории. 17

П. 5. Скорость Средняя скорость – ВФВ, характеризующая быстроту перемещения тела в пространстве, численно равная отношению вектора перемещения к интервалу времени, за который это перемещение было совершено, 18

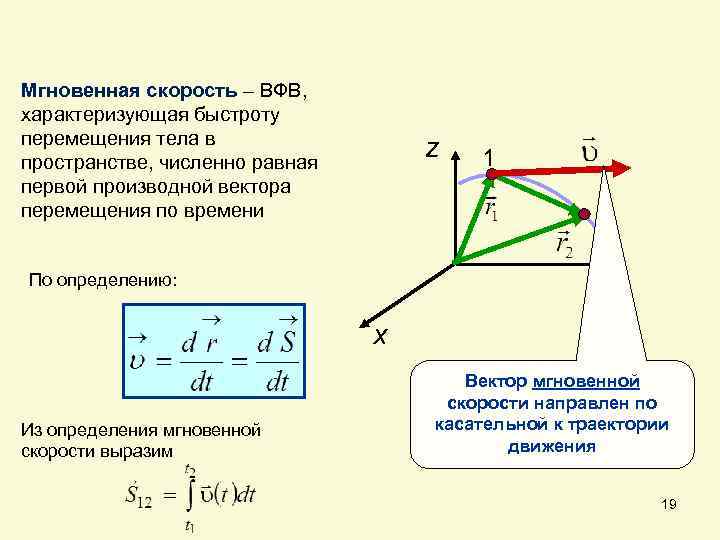Мгновенная скорость – ВФВ, характеризующая быстроту перемещения тела в пространстве, численно равная первой производной вектора перемещения по времени z 1 2 По определению: y x Из определения мгновенной скорости выразим Вектор мгновенной скорости направлен по касательной к траектории движения 19

П. 6. УСКОРЕНИЕ Ускорение – ВФВ, характеризующая быстроту изменения скорости по величине и направлению Среднее ускорение – ВФВ, характеризующая быстроту изменения скорости, численно равная отношению изменения вектора скорости ( ) к интервалу времени ( t ), за который это изменение произошло 20

Мгновенное ускорение – ВФВ, характеризующая быстроту изменения скорости, численно равная первой производной вектора скорости по времени По определению: Разложим вектор изменения скорости на две составляющие Разделим левую и правую части на t и перейдем к пределу при t 0. 21

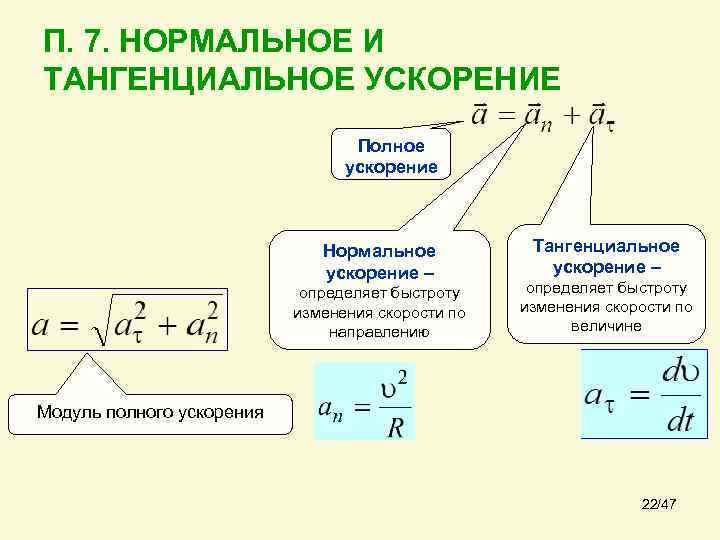П. 7. НОРМАЛЬНОЕ И ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ Полное ускорение Нормальное ускорение – определяет быстроту изменения скорости по направлению Тангенциальное ускорение – определяет быстроту изменения скорости по величине Модуль полного ускорения 22/47

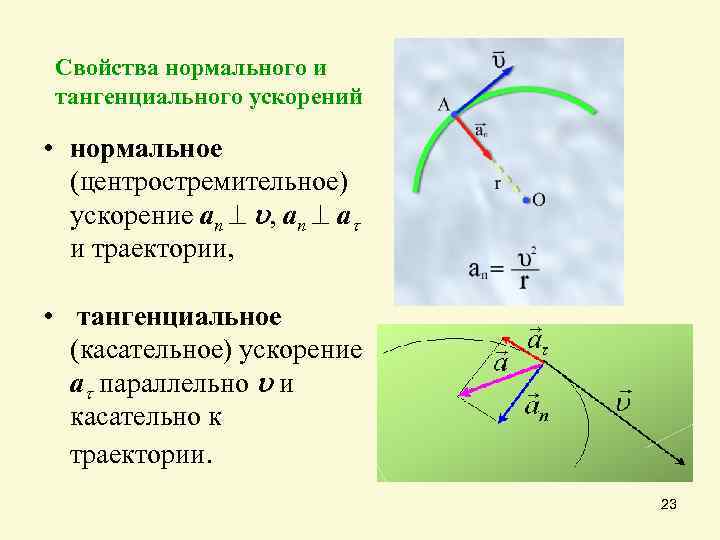Свойства нормального и тангенциального ускорений • нормальное (центростремительное) ускорение an , an a и траектории, • тангенциальное (касательное) ускорение a параллельно и касательно к траектории. 23

24

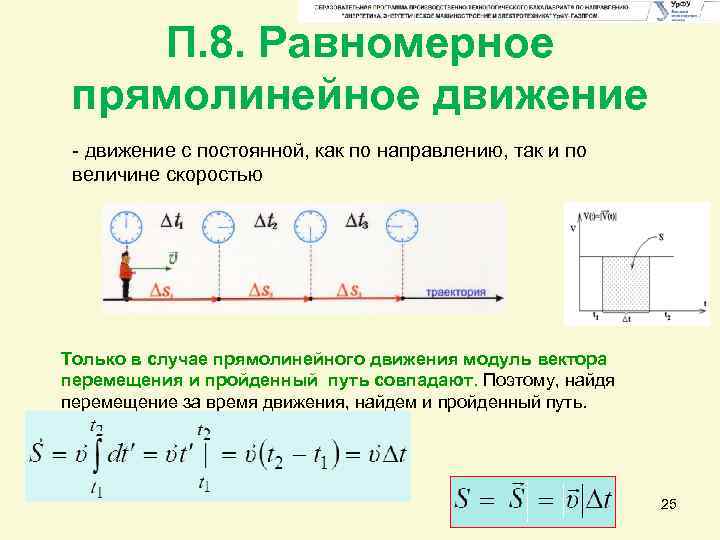П. 8. Равномерное прямолинейное движение с постоянной, как по направлению, так и по величине скоростью Только в случае прямолинейного движения модуль вектора перемещения и пройденный путь совпадают. Поэтому, найдя перемещение за время движения, найдем и пройденный путь. 25

Графическое представление равномерного прямолинейного движения 26

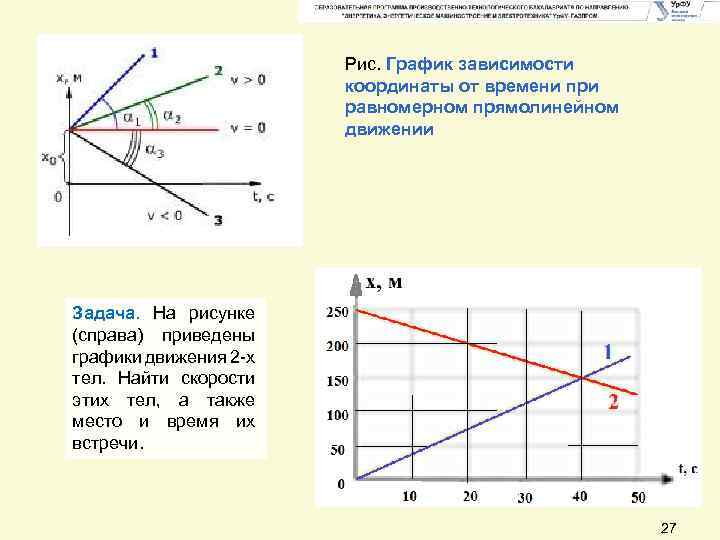Рис. График зависимости координаты от времени при равномерном прямолинейном движении Задача. На рисунке (справа) приведены графики движения 2 х тел. Найти скорости этих тел, а также место и время их встречи. 27

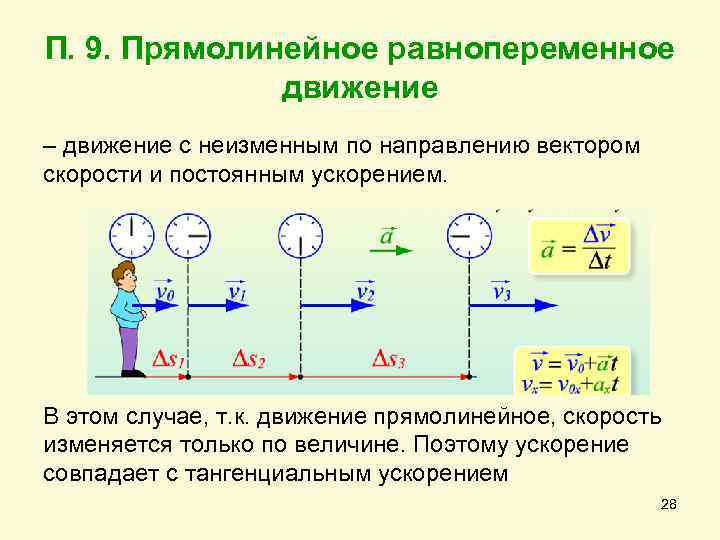П. 9. Прямолинейное равнопеременное движение – движение с неизменным по направлению вектором скорости и постоянным ускорением. В этом случае, т. к. движение прямолинейное, скорость изменяется только по величине. Поэтому ускорение совпадает с тангенциальным ускорением 28

Характеристики прямолинейного равнопеременного движения 29

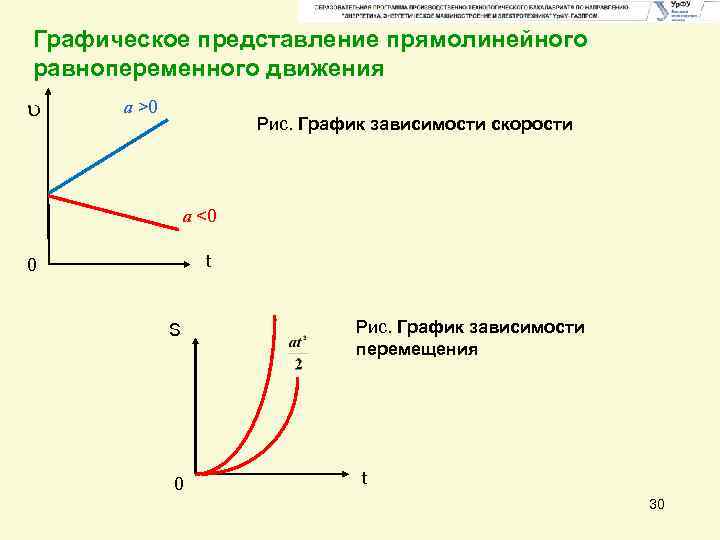Графическое представление прямолинейного равнопеременного движения a >0 Рис. График зависимости скорости a <0 t 0 S 0 Рис. График зависимости перемещения t 30

П. 10. КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Эксперимент с линейкой Вывод: введенные ранее линейные характеристики движения (такие как перемещение, путь, скорость и ускорение) не являются удобными для описания вращения тела. Их значения для разных точек одного и того же тела отличны друг от друга. линейные характеристики движения, оставаясь правильными, верными, не характеризуют вращение тела как целого. Для удобства описания вращательного движения вводятся угловые переменные: Вращение точки по окружности описывают, указывая угол поворота радиуса-вектора. Быстрота этого поворота описывается угловой скоростью Быстрота изменения угловой скорости определяется угловым ускорением . 31

Угловое перемещение (d ) – вектор, численно равный (т. е. по модулю) бесконечно малому углу поворота тела (d ) и направленный вдоль оси вращения так, что если смотреть с его конца – вращение должно происходить против часовой стрелки. 32

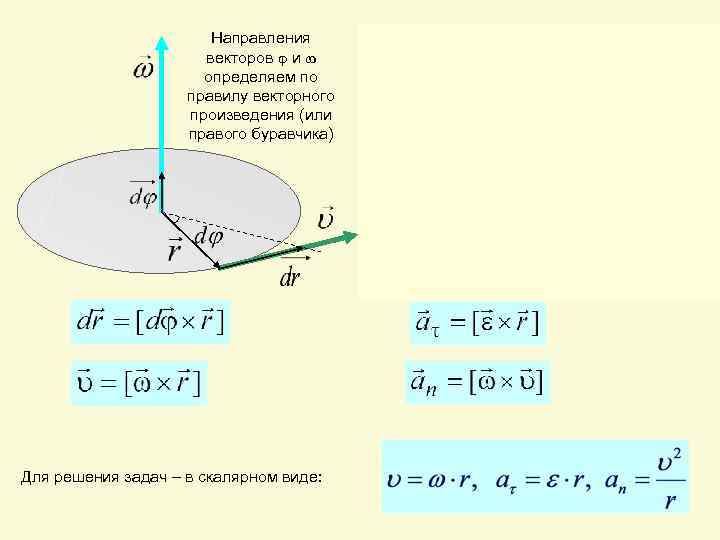Направления векторов и определяем по правилу векторного произведения (или правого буравчика) Для решения задач – в скалярном виде:

Поступательное движение Вращательное движение 34

Галилео Галилей 1564 1642 Исаак Ньютон 1642 1727 ДИНАМИКА поступательного движения тел В основе динамики лежат три закона Ньютона, которые являются опытными законами.

11. Инертность. Масса Инертность (тела) – стремление тела сохранять состояние покоя или равномерного прямолинейного движения. Масса (тела) – СФВ, являющаяся мерой инертности тела. Обозначение массы тела m, и размерность в Международной системе единиц (СИ) - килограмм ([m]= кг). 36

В классической механике: 1) Масса не зависит от состояния движения материальной точки 2) Масса – величина аддитивная (масса системы материальных точек равна сумме масс всех материальных точек, входящих в ее состав) 3) Масса замкнутой системы остается неизменной при любых процессах, происходящих в этой системе. Масса однородного тела (такое тело, плотность которого одинакова во всех его точках) Масса неоднородного тела 37

12. Импульс Из опыта известно, что одно и то же действие на разные тела ведет к одинаково му изменению некоторой векторной физической величины, численно равной произведению массы на вектор скорости: - импульс тела. Размерность импульса кг м/с. Фундаментальная величина в физике! 38

13. Сила • Сила – ВФВ, характеризующая действие одного тела на другое, в результате которого тела приобретают ускорение или деформируются, численно равная скорости изменения импульса тела (испытывающего это действие). 39

Понятие силы служит для обозначения величины и направления механического воздействия одного тела на другое. Вектор силы изображается направленным отрезком, начинающимся в точке приложения силы и направленным в сторону действия силы. Сила измеряется в ньютонах 1 Н = 1 кг м/с2 Динамическое проявление силы – изменение скорости движения; статическое проявление силы – деформация. 40

14. Деформации • Деформацией называется из менение формы и/или разме ров тела. Причиной деформации являются действующие силы. • Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называ ется упругой. Если размеры и/или форма не восстанавли ваются, то деформация называется неупругой или пластичной.

15. ПЕРВЫЙ ЗАКОН НЬЮТОНА (ЗАКОН ИНЕРЦИИ) Существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, если на него не действуют силы или действие всех сил компенсировано.

I закон Ньютона выполняется не во всякой системе отсчета. • Система отсчета, относительно которой материальная точка, свободная от внешних воздействий, покоится или движется равномерно и прямолинейно называется инерциальной системой отсчета. Любые 2 инерциальные системы отсчета могут двигаться относительно друга только равномерно и прямолинейно. Экспериментально установлено: гелиоцентрическая система отсчета – инерциальная СО. Лабораторная СО, связанная с Землей, строго говоря, не инерциальна.

16. ВТОРОЙ ЗАКОН НЬЮТОНА (уравнение движения материальной точки) Этот закон указывает на то, как изменяется механическое движение МТ под действием приложенных к ней сил. Он справедлив только в ИСО! Его формулировка: Равнодействующая всех сил, действующих на тело, равна быстроте (скорости) изменения импульса этого тела. 44

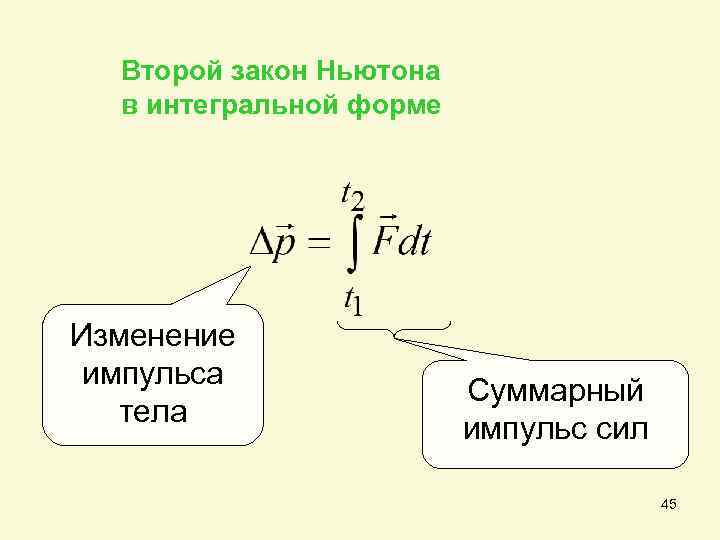Второй закон Ньютона в интегральной форме Изменение импульса тела Суммарный импульс сил 45

Другая формулировка II закона Ньютона (основной закон динамики поступательного движения МТ) Ускорение движения тела равно отношению равнодействующей всех сил, действующих на это тело, к массе этого тела и направлено вдоль линии равнодействующей этих сил. 46

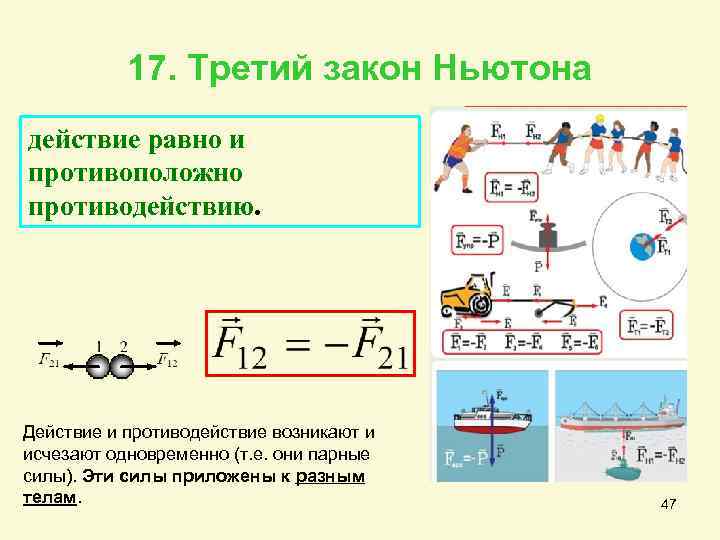17. Третий закон Ньютона действие равно и противоположно противодействию. Действие и противодействие возникают и исчезают одновременно (т. е. они парные силы). Эти силы приложены к разным телам. 47

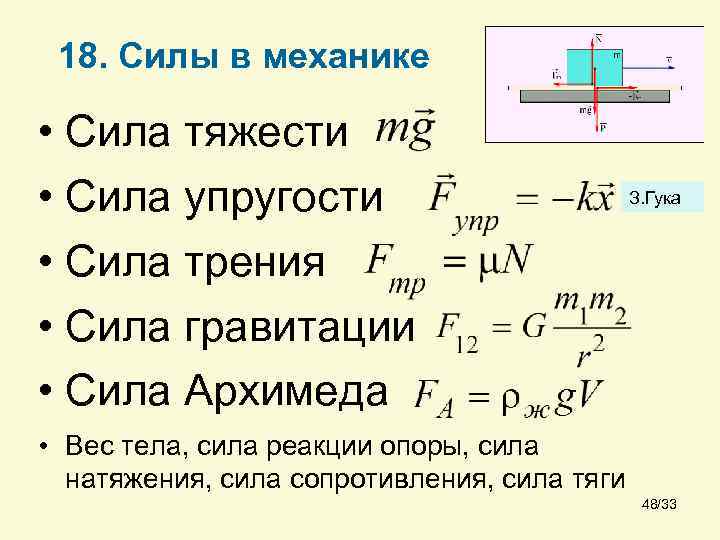18. Силы в механике • Сила тяжести • Сила упругости • Сила трения • Сила гравитации • Сила Архимеда З. Гука • Вес тела, сила реакции опоры, сила натяжения, сила сопротивления, сила тяги 48/33

ДИНАМИКА вращательного движения тел Цель Ввести физические величины (момент силы, момент импульса, момент инерции ) для описания динамики вращения АТТ. Сформулировать основной закон динамики вращательного движения

19. Момент силы - вектор, характеризующий действие силы относительно некоторой точки, численно равный произведению модуля силы на плечо ( l ) где l – плечо силы, равное длине перпендикуляра, опущенного из точки (относительно которой вычисляется момент силы) на линию действия силы 50

Так как вектор момента силы перпендикулярен вектору силы и радиус вектору, проведенному в точку приложения силы из точки, относительно которой он вычисляется. а плечо то выражение мож но записать в векторном виде: Вектор момента силы направлен так, что если смотреть с его конца, то вращение, к которому приводит эта сила, дол жно происходить против часовой стрелки. 51

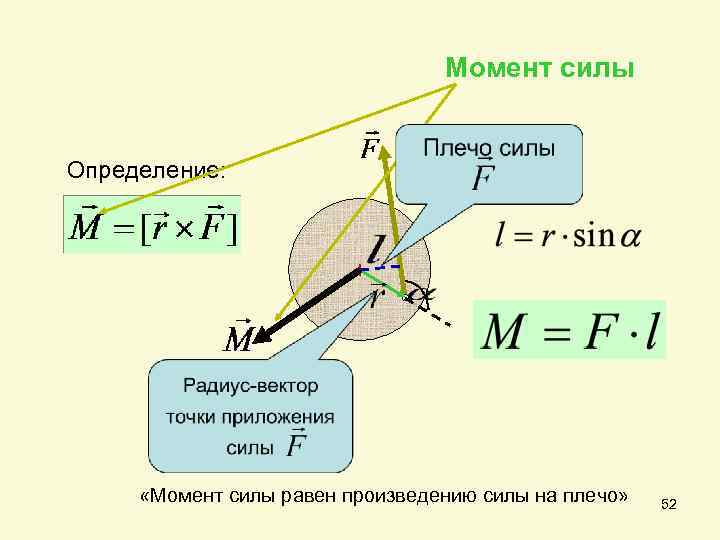Момент силы Определение: «Момент силы равен произведению силы на плечо» 52

20. Момент импульса м. т. Пусть МТ массой m вращается вокруг некоторой оси Оz и испытывает действие нескольких сил. Момент равнодействующей F этих сил относительно некоторой точки O, лежащей на оси вращения, определяется выражением Применяя II закон Ньютона, получим М момент равнодействующей всех сил действующих на материальную точку, r радиус вектор, а p импульс материальной точки. 53/21

Преобразуем выражение: вынесем знак производной за знак векторного произведения Введем в рассмотрение новую физическую величину называемую вектором момента импульса МТ относительно некоторой неподвижной точки О. Уравнение моментов или основной закон динамики вращательного движения: 54

Помним: Векторы L и M – динамические характеристики вращательного движения, всегда направлены вдоль оси вращения (на данном рисунке ось вращения – ось Oz). Причем, L определяется направлением вращения, как и , а направление M зависит от того, ускоряется или замедляется вращение. 55

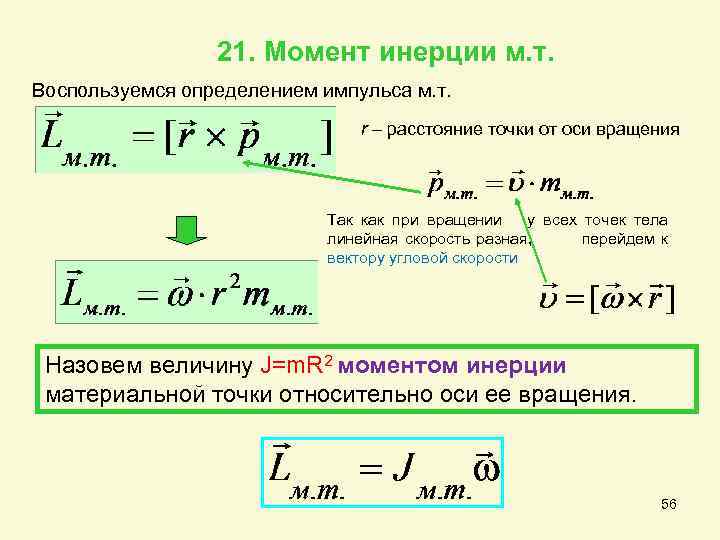21. Момент инерции м. т. Воспользуемся определением импульса м. т. r – расстояние точки от оси вращения Так как при вращении у всех точек тела линейная скорость разная, перейдем к вектору угловой скорости Назовем величину J=m. R 2 моментом инерции материальной точки относительно оси ее вращения. 56

22. Момент инерции абсолютно твердого тела Момент импульса а. т. т. складывается из моментов импульса его фрагментов • Момент инерции J тела относительно оси вращения – СФВ, характеризующая инертность тела относительно вращения, численно равная где r – расстояние от оси z до dm. (Сравним: p =m для поступательного движения). где r радиус кривизны траектории движения объема d. V (т. е. радиус окружности или дуги окружности, вдоль которой движется объем d. V). 57

По формуле не всегда просто рассчитать момент инерции тел произвольной формы. Наиболее легко эта задача решается для тел простых форм, вращающихся вокруг оси, проходящей через центр инерции тела Jc. В этом случае Jc вычисляется по формуле: Значения коэффициента k приведены на следующем слайде

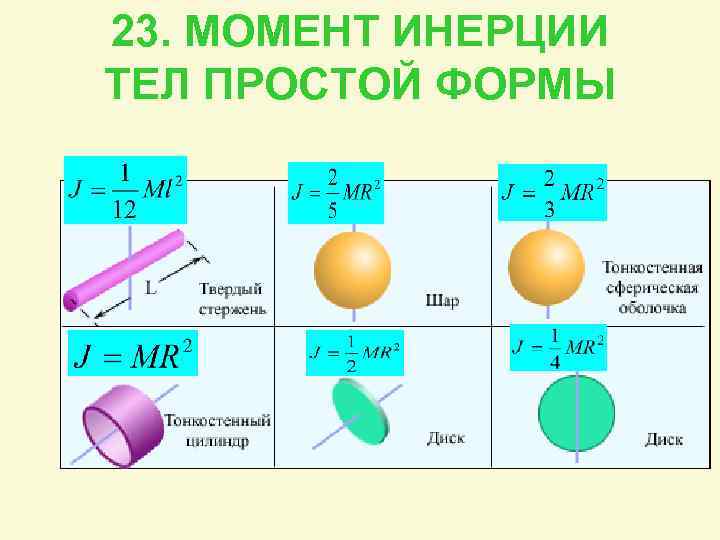23. МОМЕНТ ИНЕРЦИИ ТЕЛ ПРОСТОЙ ФОРМЫ

24. Основное уравнение динамики вращательного движения 60

25. ТЕОРЕМА ШТЕЙНЕРА При вычислении момента инерции тела, вращающегося вокруг оси, не проходящей через центр инерции, следует пользоваться теоремой о параллельном переносе осей или теоремой Штейнера Z ω ri Y Якоб Штейнер 1796 – 1863 швецарский математик X ε

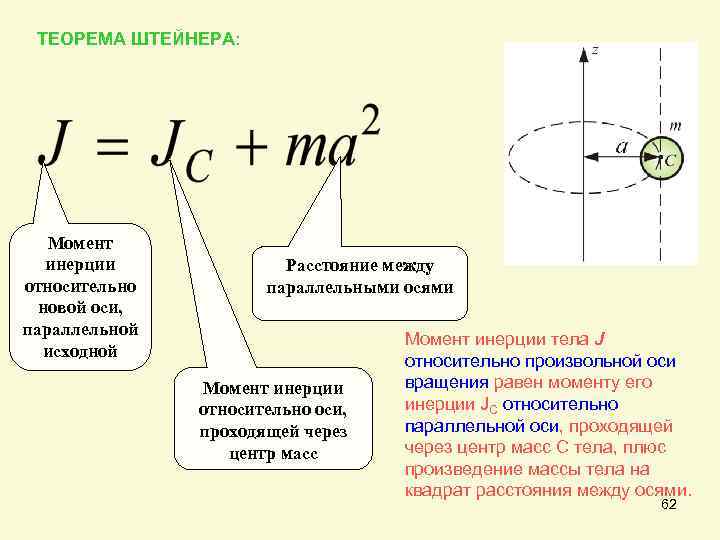ТЕОРЕМА ШТЕЙНЕРА: Момент инерции относительно новой оси, параллельной исходной Расстояние между параллельными осями Момент инерции относительно оси, проходящей через центр масс Момент инерции тела J относительно произвольной оси вращения равен моменту его инерции JС относительно параллельной оси, проходящей через центр масс С тела, плюс произведение массы тела на квадрат расстояния между осями. 62

Пример: стержень массой m, длиной l, вращается вокруг оси, проходящей через конец стержня (рис).