0904bc716fc3fc58c721ec30dd4bb1f3.ppt
- Количество слайдов: 53
 HQ Collisional energy loss at RHIC & Predictions for the LHC P. B. Gossiaux SUBATECH, UMR 6457 Université de Nantes, Ecole des Mines de Nantes, IN 2 P 3/CNRS Collaborators J. Aichelin, A. Peshier, R. Bierkandt
HQ Collisional energy loss at RHIC & Predictions for the LHC P. B. Gossiaux SUBATECH, UMR 6457 Université de Nantes, Ecole des Mines de Nantes, IN 2 P 3/CNRS Collaborators J. Aichelin, A. Peshier, R. Bierkandt
 GOAL of the STUDY Recent revival of the collisional energy loss in order to explain the large "thermalization" of heavy quarks in Au+Au collisions at RHIC at low and intermediate p. T Most often, however: 1) No "real" p. QCD implemented No running as (cf. previous work of Peshier), "crude" IR regulator 2) Fokker – Planck equation… Might not be applicable : "hard" transfers, # of collisions not systematically large at the periphery … or detailed balance not satisfied (just E loss, no E gain ) 1
GOAL of the STUDY Recent revival of the collisional energy loss in order to explain the large "thermalization" of heavy quarks in Au+Au collisions at RHIC at low and intermediate p. T Most often, however: 1) No "real" p. QCD implemented No running as (cf. previous work of Peshier), "crude" IR regulator 2) Fokker – Planck equation… Might not be applicable : "hard" transfers, # of collisions not systematically large at the periphery … or detailed balance not satisfied (just E loss, no E gain ) 1
 2 From a more phenomenological point of view: 3) Need to crank up the 2 2 cross sections in order to reproduce the RAA 4) Difficulty ( « challenge to the models » ) to reproduce both the RAA and the v 2 without "exotic" processes, like in-QGP resonances. Our approach: consider heavy-Q evolution in QGP according to Boltzmann equation with improved 2 2 cross sections and look whether this helps solving points 3) and 4) If yes: consider other observables and make predictions for LHC
2 From a more phenomenological point of view: 3) Need to crank up the 2 2 cross sections in order to reproduce the RAA 4) Difficulty ( « challenge to the models » ) to reproduce both the RAA and the v 2 without "exotic" processes, like in-QGP resonances. Our approach: consider heavy-Q evolution in QGP according to Boltzmann equation with improved 2 2 cross sections and look whether this helps solving points 3) and 4) If yes: consider other observables and make predictions for LHC
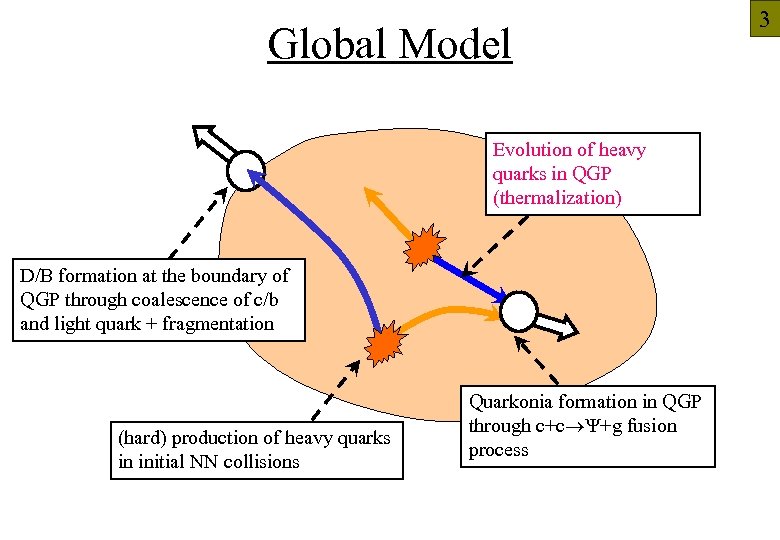 3 Global Model Evolution of heavy quarks in QGP (thermalization) D/B formation at the boundary of QGP through coalescence of c/b and light quark + fragmentation (hard) production of heavy quarks in initial NN collisions Quarkonia formation in QGP through c+c Y+g fusion process
3 Global Model Evolution of heavy quarks in QGP (thermalization) D/B formation at the boundary of QGP through coalescence of c/b and light quark + fragmentation (hard) production of heavy quarks in initial NN collisions Quarkonia formation in QGP through c+c Y+g fusion process
 Heavy quarks in QGP In p. QGP, heavy quarks are assumed to interact with partons of type "i" (massless quarks and gluons) with local 2 2 rate: Ri Associated transport coefficient (drag, energy loss, …) depend on the QGP macroscopic parameters (T, v, m) at a given 4 -position (t, x). These parameters are extracted from a "standard" hydro-model (Heinz & Kolb: boost invariant) We follow the hydro evolution of partons and sample the rates Ri "on the way", performing the Qq Q'q' & Qg Q'g' collisions: MC approach 4
Heavy quarks in QGP In p. QGP, heavy quarks are assumed to interact with partons of type "i" (massless quarks and gluons) with local 2 2 rate: Ri Associated transport coefficient (drag, energy loss, …) depend on the QGP macroscopic parameters (T, v, m) at a given 4 -position (t, x). These parameters are extracted from a "standard" hydro-model (Heinz & Kolb: boost invariant) We follow the hydro evolution of partons and sample the rates Ri "on the way", performing the Qq Q'q' & Qg Q'g' collisions: MC approach 4
 Oldies
Oldies
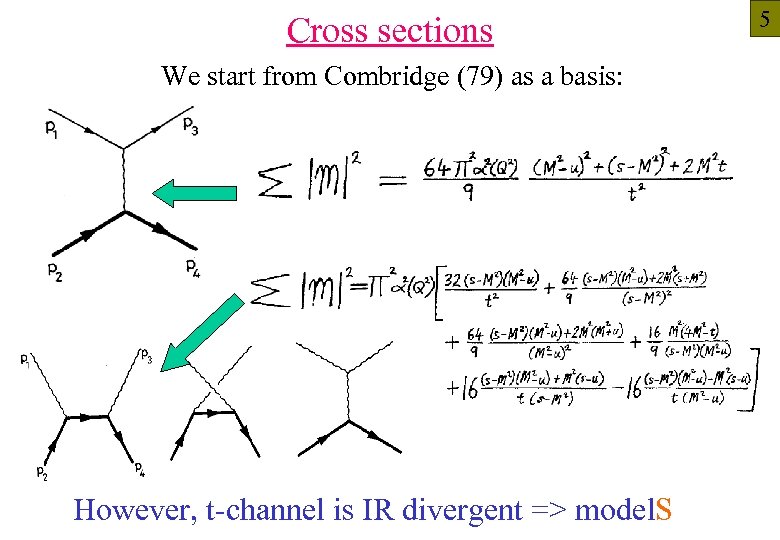 Cross sections We start from Combridge (79) as a basis: However, t-channel is IR divergent => model. S 5
Cross sections We start from Combridge (79) as a basis: However, t-channel is IR divergent => model. S 5
 Naïve regulating of IR divergence: 1 1 With m(T) or m(t) Models A/B: no as - running m 2(T) = m. D 2 = 4 pas(1+3/6)x. T 2 Customary choice as(Q 2) 0. 3 (mod A) as(2 p. T) (mod B) ( 0. 3) T(Me. V) p(Ge. V/c) 10 20 200 400 0. 18 0. 35 0. 27 0. 54 … of the order of a few % ! 6
Naïve regulating of IR divergence: 1 1 With m(T) or m(t) Models A/B: no as - running m 2(T) = m. D 2 = 4 pas(1+3/6)x. T 2 Customary choice as(Q 2) 0. 3 (mod A) as(2 p. T) (mod B) ( 0. 3) T(Me. V) p(Ge. V/c) 10 20 200 400 0. 18 0. 35 0. 27 0. 54 … of the order of a few % ! 6
 Other hypothesis / ingredients of the model • Au–Au collisions at 200 AGe. V: 17 c-cbar pairs in central collisions • Q distributions: adjusted to NLO & FONLL • Cronin effect (0. 2 Ge. V 2/coll. ). • No force on HQ before thermalization of QGP (0. 6 fm/c) • Evolution according to Bjorken time until the beginning or the end of the cross-over • Q-Fragmentation and decay e as in Cacciari, Nason & Vogt 2005. • No D (B) interaction in hadronic phase 7
Other hypothesis / ingredients of the model • Au–Au collisions at 200 AGe. V: 17 c-cbar pairs in central collisions • Q distributions: adjusted to NLO & FONLL • Cronin effect (0. 2 Ge. V 2/coll. ). • No force on HQ before thermalization of QGP (0. 6 fm/c) • Evolution according to Bjorken time until the beginning or the end of the cross-over • Q-Fragmentation and decay e as in Cacciari, Nason & Vogt 2005. • No D (B) interaction in hadronic phase 7
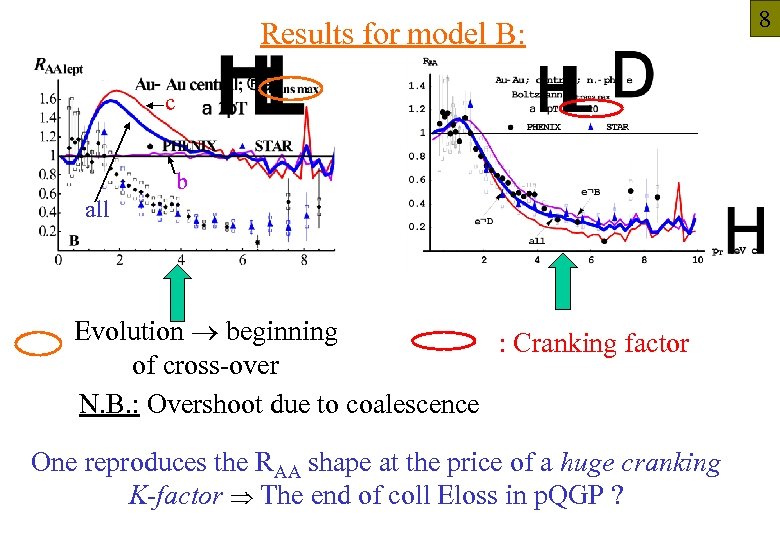 Results for model B: c b all Evolution beginning : Cranking factor of cross-over N. B. : Overshoot due to coalescence One reproduces the RAA shape at the price of a huge cranking K-factor The end of coll Eloss in p. QGP ? 8
Results for model B: c b all Evolution beginning : Cranking factor of cross-over N. B. : Overshoot due to coalescence One reproduces the RAA shape at the price of a huge cranking K-factor The end of coll Eloss in p. QGP ? 8
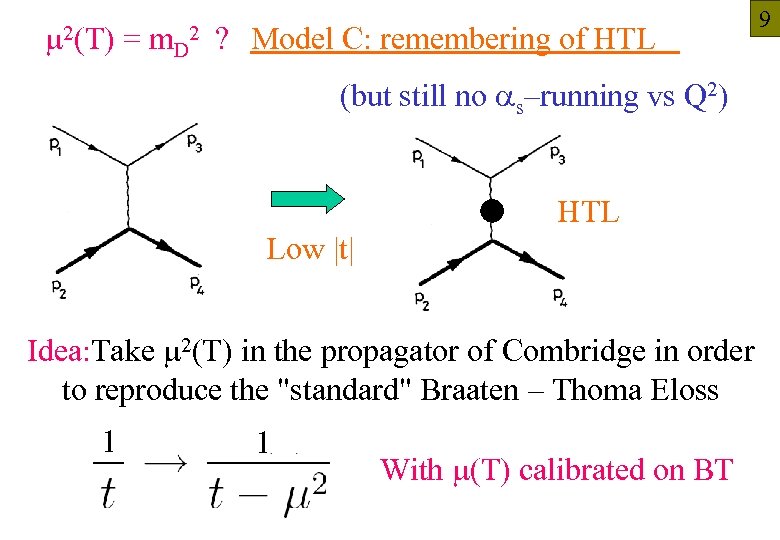 m 2(T) = m. D 2 ? Model C: remembering of HTL 9 (but still no as–running vs Q 2) HTL Low |t| Idea: Take m 2(T) in the propagator of Combridge in order to reproduce the "standard" Braaten – Thoma Eloss 1 1 With m(T) calibrated on BT
m 2(T) = m. D 2 ? Model C: remembering of HTL 9 (but still no as–running vs Q 2) HTL Low |t| Idea: Take m 2(T) in the propagator of Combridge in order to reproduce the "standard" Braaten – Thoma Eloss 1 1 With m(T) calibrated on BT
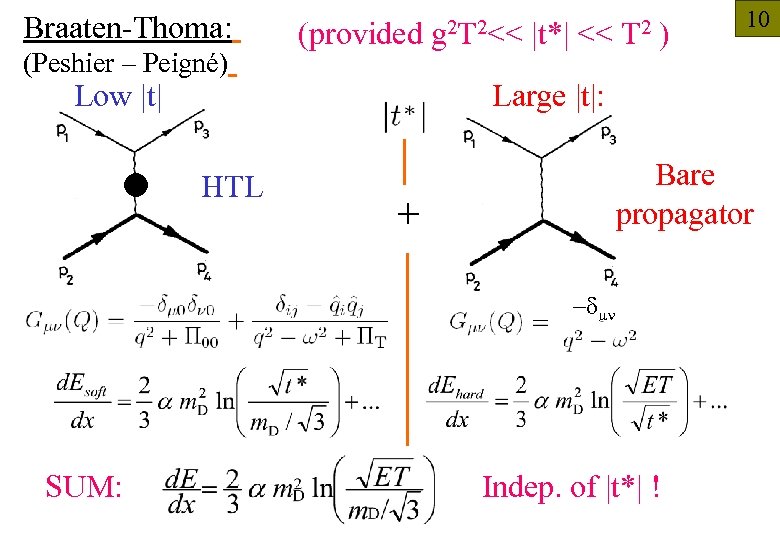 Braaten-Thoma: (Peshier – Peigné) Low |t| HTL (provided g 2 T 2<< |t*| << T 2 ) Large |t|: Bare propagator + -dmn SUM: 10 Indep. of |t*| !
Braaten-Thoma: (Peshier – Peigné) Low |t| HTL (provided g 2 T 2<< |t*| << T 2 ) Large |t|: Bare propagator + -dmn SUM: 10 Indep. of |t*| !
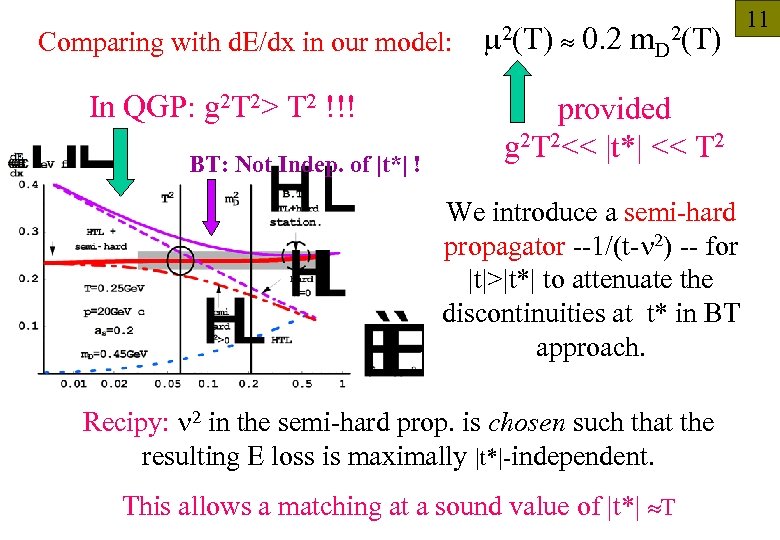 Comparing with d. E/dx in our model: In QGP: g 2 T 2> T 2 !!! BT: Not Indep. of |t*| ! m 2(T) 0. 2 m. D 2(T) 11 provided g 2 T 2<< |t*| << T 2 We introduce a semi-hard propagator --1/(t-n 2) -- for |t|>|t*| to attenuate the discontinuities at t* in BT approach. Recipy: n 2 in the semi-hard prop. is chosen such that the resulting E loss is maximally |t*|-independent. This allows a matching at a sound value of |t*| T
Comparing with d. E/dx in our model: In QGP: g 2 T 2> T 2 !!! BT: Not Indep. of |t*| ! m 2(T) 0. 2 m. D 2(T) 11 provided g 2 T 2<< |t*| << T 2 We introduce a semi-hard propagator --1/(t-n 2) -- for |t|>|t*| to attenuate the discontinuities at t* in BT approach. Recipy: n 2 in the semi-hard prop. is chosen such that the resulting E loss is maximally |t*|-independent. This allows a matching at a sound value of |t*| T
 Model C: no Q 2 – running, optimal m 2 Also Refered as mod C THEN: Optimal choice of m in our OBE model: as(2 p. T) m 2(T) 0. 15 m. D 2(T) with m. D 2 = 4 pas(2 p. T)(1+3/6)x. T 2 T(Me. V) p(Ge. V/c) 10 20 200 0. 36 0. 49 (0. 18) (0. 27) 0. 70 0. 98 (0. 35) (0. 54) 400 … factor 2 increase w. r. t. mod B 12
Model C: no Q 2 – running, optimal m 2 Also Refered as mod C THEN: Optimal choice of m in our OBE model: as(2 p. T) m 2(T) 0. 15 m. D 2(T) with m. D 2 = 4 pas(2 p. T)(1+3/6)x. T 2 T(Me. V) p(Ge. V/c) 10 20 200 0. 36 0. 49 (0. 18) (0. 27) 0. 70 0. 98 (0. 35) (0. 54) 400 … factor 2 increase w. r. t. mod B 12
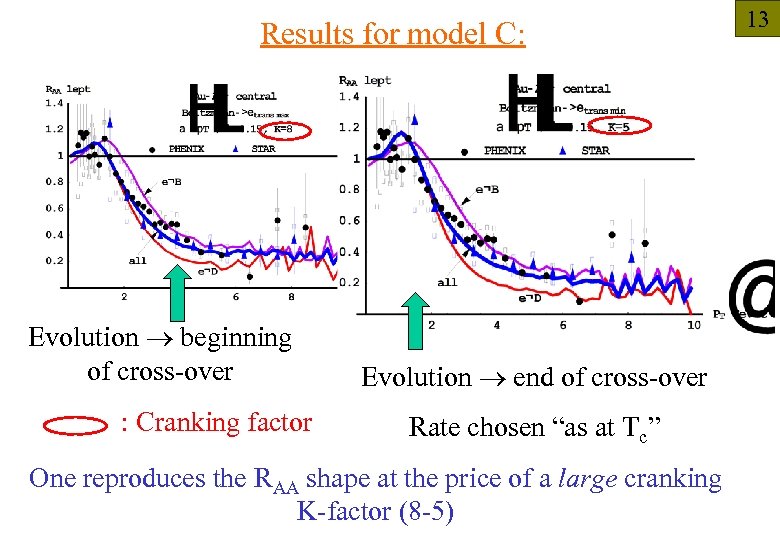 Results for model C: Evolution beginning of cross-over : Cranking factor Evolution end of cross-over Rate chosen “as at Tc” One reproduces the RAA shape at the price of a large cranking K-factor (8 -5) 13
Results for model C: Evolution beginning of cross-over : Cranking factor Evolution end of cross-over Rate chosen “as at Tc” One reproduces the RAA shape at the price of a large cranking K-factor (8 -5) 13
 More recently (2 -3 years now)
More recently (2 -3 years now)
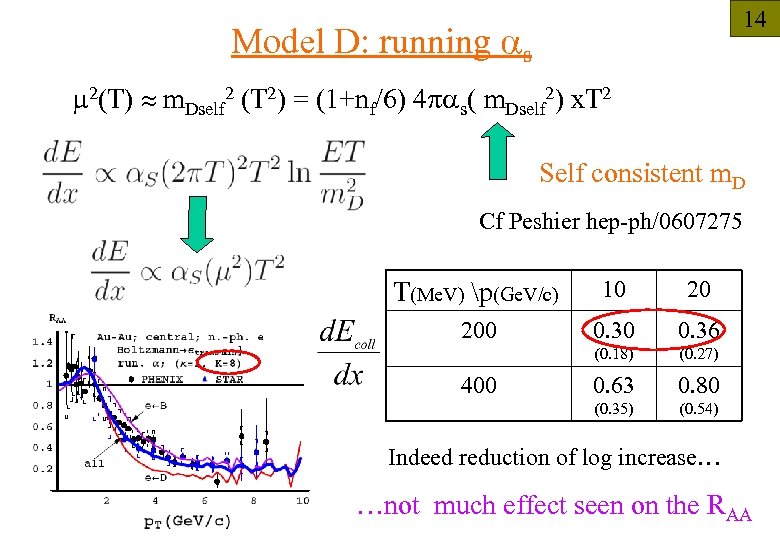 14 Model D: running as m 2(T) m. Dself 2 (T 2) = (1+nf/6) 4 pas( m. Dself 2) x. T 2 Self consistent m. D Cf Peshier hep-ph/0607275 T(Me. V) p(Ge. V/c) 10 20 200 0. 30 0. 36 (0. 18) (0. 27) 0. 63 0. 80 (0. 35) (0. 54) 400 Indeed reduction of log increase… …not much effect seen on the RAA
14 Model D: running as m 2(T) m. Dself 2 (T 2) = (1+nf/6) 4 pas( m. Dself 2) x. T 2 Self consistent m. D Cf Peshier hep-ph/0607275 T(Me. V) p(Ge. V/c) 10 20 200 0. 30 0. 36 (0. 18) (0. 27) 0. 63 0. 80 (0. 35) (0. 54) 400 Indeed reduction of log increase… …not much effect seen on the RAA
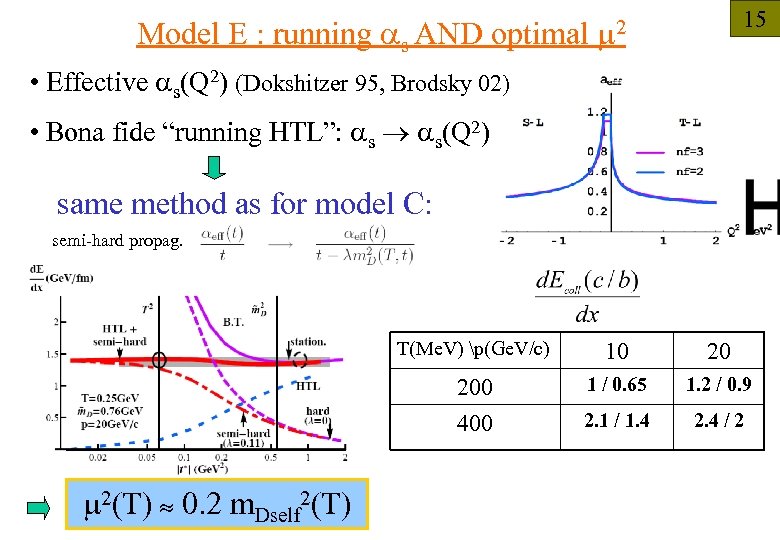 Model E : running as 15 AND optimal m 2 • Effective as(Q 2) (Dokshitzer 95, Brodsky 02) • Bona fide “running HTL”: as as(Q 2) same method as for model C: semi-hard propag. T(Me. V) p(Ge. V/c) 20 200 400 m 2(T) 0. 2 m. Dself 2(T) 10 1 / 0. 65 1. 2 / 0. 9 2. 1 / 1. 4 2. 4 / 2
Model E : running as 15 AND optimal m 2 • Effective as(Q 2) (Dokshitzer 95, Brodsky 02) • Bona fide “running HTL”: as as(Q 2) same method as for model C: semi-hard propag. T(Me. V) p(Ge. V/c) 20 200 400 m 2(T) 0. 2 m. Dself 2(T) 10 1 / 0. 65 1. 2 / 0. 9 2. 1 / 1. 4 2. 4 / 2
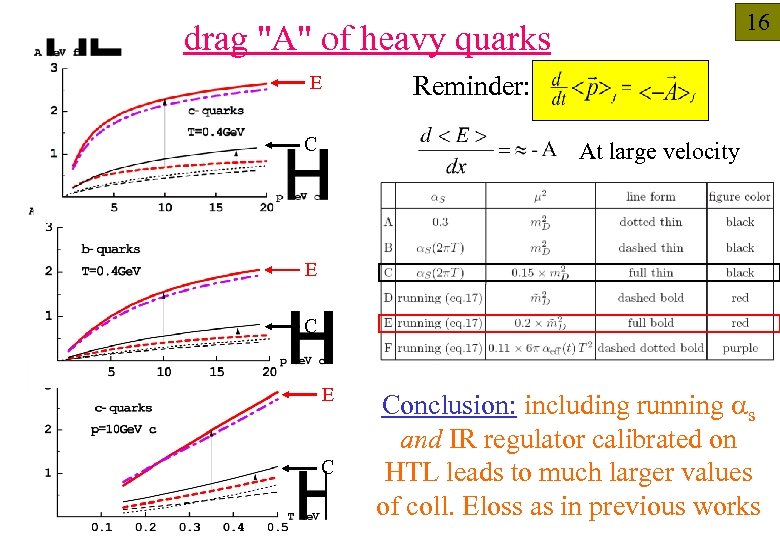 16 drag "A" of heavy quarks E C Reminder: At large velocity E C Conclusion: including running as and IR regulator calibrated on HTL leads to much larger values of coll. Eloss as in previous works
16 drag "A" of heavy quarks E C Reminder: At large velocity E C Conclusion: including running as and IR regulator calibrated on HTL leads to much larger values of coll. Eloss as in previous works
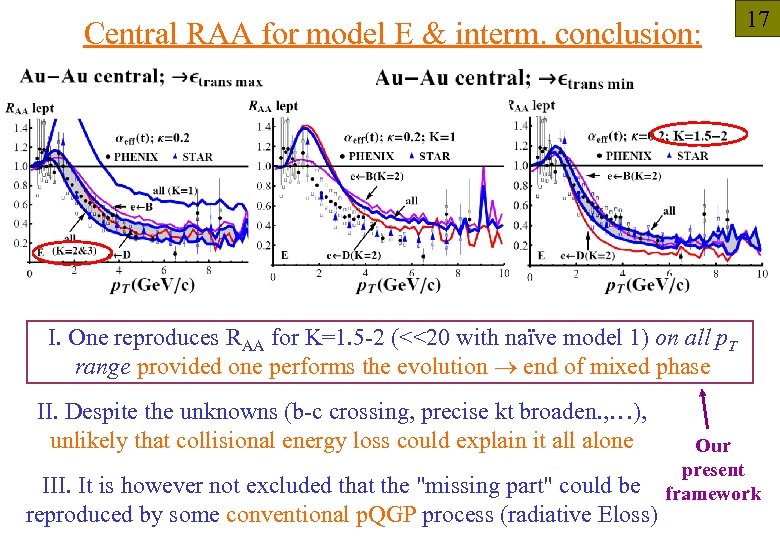 Central RAA for model E & interm. conclusion: 17 I. One reproduces RAA for K=1. 5 -2 (<<20 with naïve model 1) on all p. T range provided one performs the evolution end of mixed phase II. Despite the unknowns (b-c crossing, precise kt broaden. , …), unlikely that collisional energy loss could explain it all alone III. It is however not excluded that the "missing part" could be reproduced by some conventional p. QGP process (radiative Eloss) Our present framework
Central RAA for model E & interm. conclusion: 17 I. One reproduces RAA for K=1. 5 -2 (<<20 with naïve model 1) on all p. T range provided one performs the evolution end of mixed phase II. Despite the unknowns (b-c crossing, precise kt broaden. , …), unlikely that collisional energy loss could explain it all alone III. It is however not excluded that the "missing part" could be reproduced by some conventional p. QGP process (radiative Eloss) Our present framework
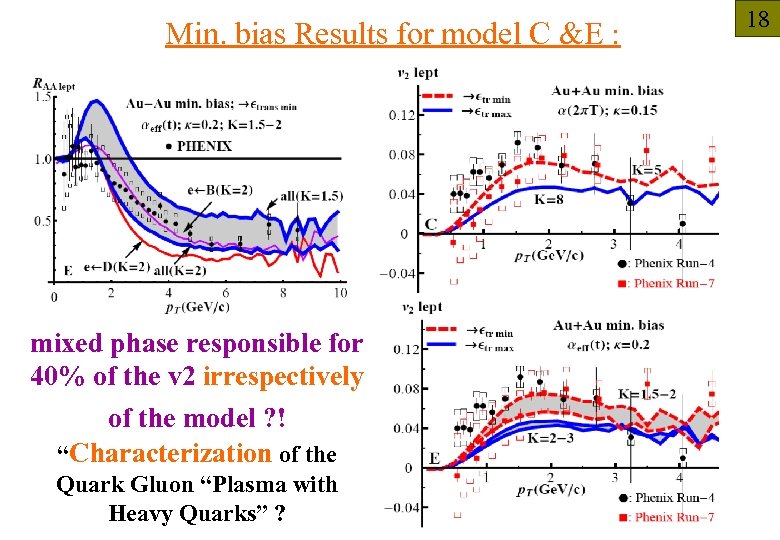 Min. bias Results for model C &E : mixed phase responsible for 40% of the v 2 irrespectively of the model ? ! “Characterization of the Quark Gluon “Plasma with Heavy Quarks” ? 18
Min. bias Results for model C &E : mixed phase responsible for 40% of the v 2 irrespectively of the model ? ! “Characterization of the Quark Gluon “Plasma with Heavy Quarks” ? 18
 Could other observables help ?
Could other observables help ?
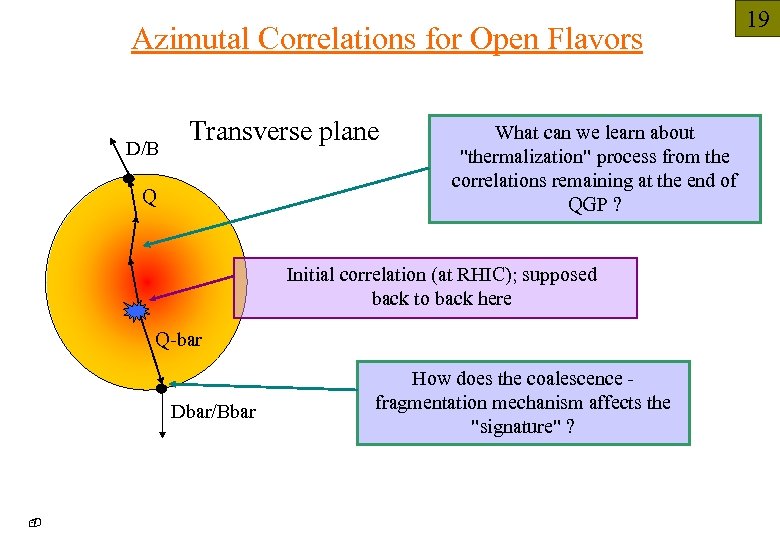 Azimutal Correlations for Open Flavors D/B Transverse plane Q What can we learn about "thermalization" process from the correlations remaining at the end of QGP ? Initial correlation (at RHIC); supposed back to back here Q-bar Dbar/Bbar - How does the coalescence - fragmentation mechanism affects the "signature" ? 19
Azimutal Correlations for Open Flavors D/B Transverse plane Q What can we learn about "thermalization" process from the correlations remaining at the end of QGP ? Initial correlation (at RHIC); supposed back to back here Q-bar Dbar/Bbar - How does the coalescence - fragmentation mechanism affects the "signature" ? 19
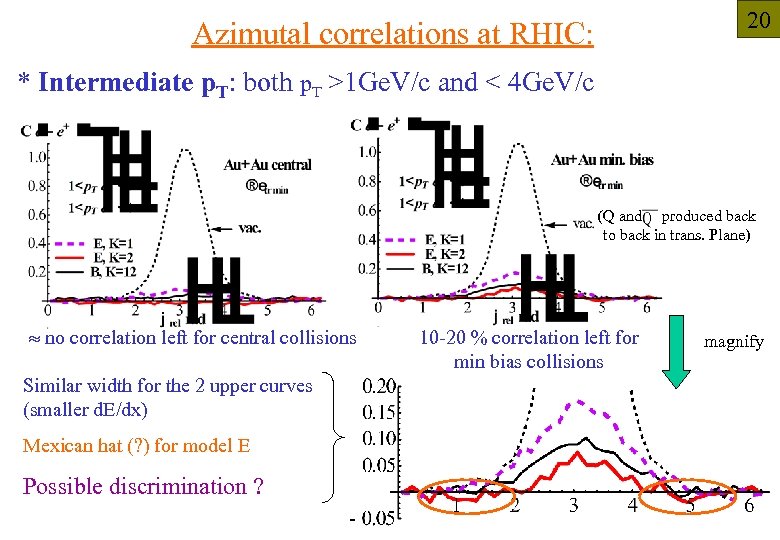 20 Azimutal correlations at RHIC: * Intermediate p. T: both p. T >1 Ge. V/c and < 4 Ge. V/c (Q and produced back to back in trans. Plane) no correlation left for central collisions Similar width for the 2 upper curves (smaller d. E/dx) Mexican hat (? ) for model E Possible discrimination ? 10 -20 % correlation left for min bias collisions magnify
20 Azimutal correlations at RHIC: * Intermediate p. T: both p. T >1 Ge. V/c and < 4 Ge. V/c (Q and produced back to back in trans. Plane) no correlation left for central collisions Similar width for the 2 upper curves (smaller d. E/dx) Mexican hat (? ) for model E Possible discrimination ? 10 -20 % correlation left for min bias collisions magnify
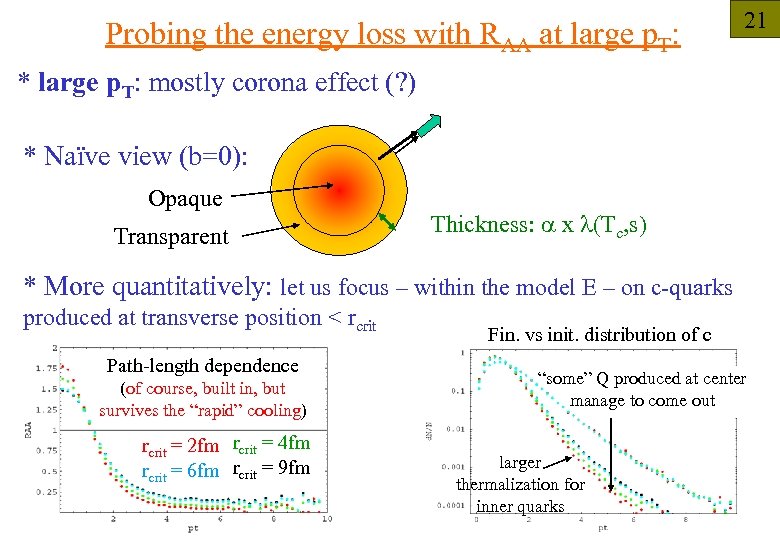 Probing the energy loss with RAA at large p. T: 21 * large p. T: mostly corona effect (? ) * Naïve view (b=0): Opaque Transparent Thickness: a x l(Tc, s) * More quantitatively: let us focus – within the model E – on c-quarks produced at transverse position < rcrit Path-length dependence (of course, built in, but survives the “rapid” cooling) rcrit = 2 fm rcrit = 4 fm rcrit = 6 fm rcrit = 9 fm Fin. vs init. distribution of c “some” Q produced at center manage to come out larger thermalization for inner quarks
Probing the energy loss with RAA at large p. T: 21 * large p. T: mostly corona effect (? ) * Naïve view (b=0): Opaque Transparent Thickness: a x l(Tc, s) * More quantitatively: let us focus – within the model E – on c-quarks produced at transverse position < rcrit Path-length dependence (of course, built in, but survives the “rapid” cooling) rcrit = 2 fm rcrit = 4 fm rcrit = 6 fm rcrit = 9 fm Fin. vs init. distribution of c “some” Q produced at center manage to come out larger thermalization for inner quarks
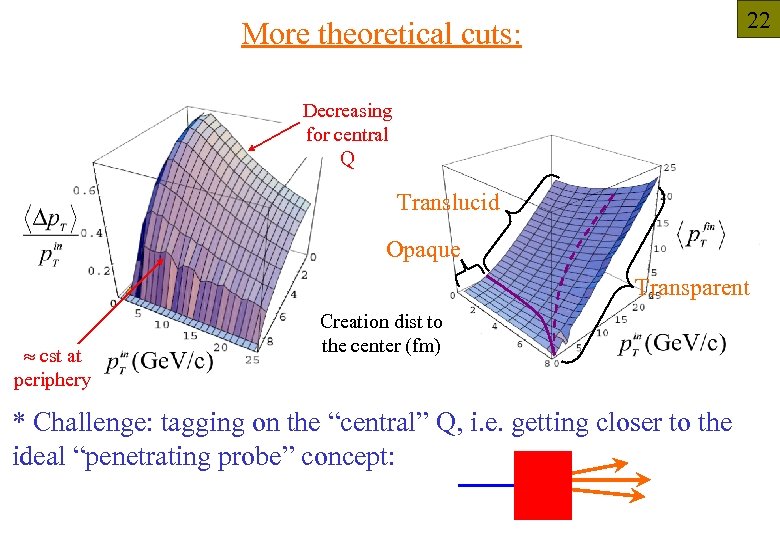 22 More theoretical cuts: Decreasing for central Q Translucid Opaque Transparent cst at periphery Creation dist to the center (fm) * Challenge: tagging on the “central” Q, i. e. getting closer to the ideal “penetrating probe” concept:
22 More theoretical cuts: Decreasing for central Q Translucid Opaque Transparent cst at periphery Creation dist to the center (fm) * Challenge: tagging on the “central” Q, i. e. getting closer to the ideal “penetrating probe” concept:
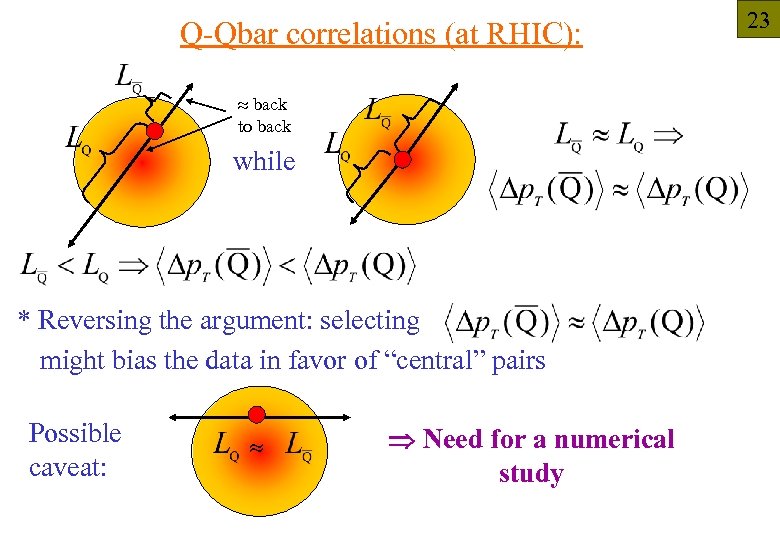 Q-Qbar correlations (at RHIC): back to back while * Reversing the argument: selecting might bias the data in favor of “central” pairs Possible caveat: Need for a numerical study 23
Q-Qbar correlations (at RHIC): back to back while * Reversing the argument: selecting might bias the data in favor of “central” pairs Possible caveat: Need for a numerical study 23
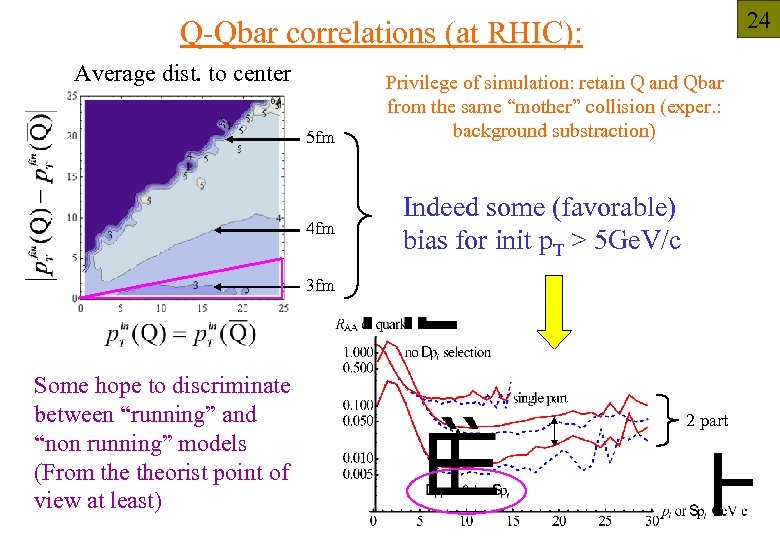 24 Q-Qbar correlations (at RHIC): Average dist. to center 5 fm 4 fm Privilege of simulation: retain Q and Qbar from the same “mother” collision (exper. : background substraction) Indeed some (favorable) bias for init p. T > 5 Ge. V/c 3 fm Some hope to discriminate between “running” and “non running” models (From theorist point of view at least) 2 part
24 Q-Qbar correlations (at RHIC): Average dist. to center 5 fm 4 fm Privilege of simulation: retain Q and Qbar from the same “mother” collision (exper. : background substraction) Indeed some (favorable) bias for init p. T > 5 Ge. V/c 3 fm Some hope to discriminate between “running” and “non running” models (From theorist point of view at least) 2 part
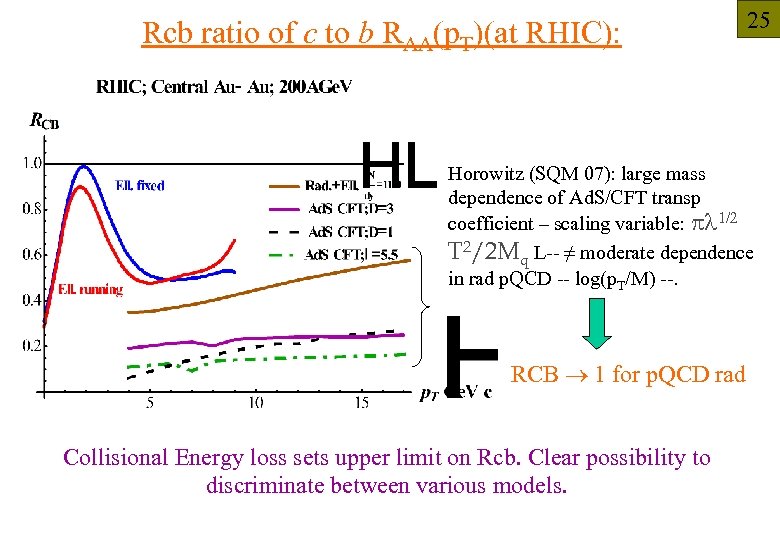 Rcb ratio of c to b RAA(p. T)(at RHIC): 25 5 fm 4 fm 3 fm Horowitz (SQM 07): large mass dependence of Ad. S/CFT transp coefficient – scaling variable: pl 1/2 T 2/2 Mq L-- ≠ moderate dependence in rad p. QCD -- log(p. T/M) --. RCB 1 for p. QCD rad Collisional Energy loss sets upper limit on Rcb. Clear possibility to discriminate between various models.
Rcb ratio of c to b RAA(p. T)(at RHIC): 25 5 fm 4 fm 3 fm Horowitz (SQM 07): large mass dependence of Ad. S/CFT transp coefficient – scaling variable: pl 1/2 T 2/2 Mq L-- ≠ moderate dependence in rad p. QCD -- log(p. T/M) --. RCB 1 for p. QCD rad Collisional Energy loss sets upper limit on Rcb. Clear possibility to discriminate between various models.
 Towards… LHC
Towards… LHC
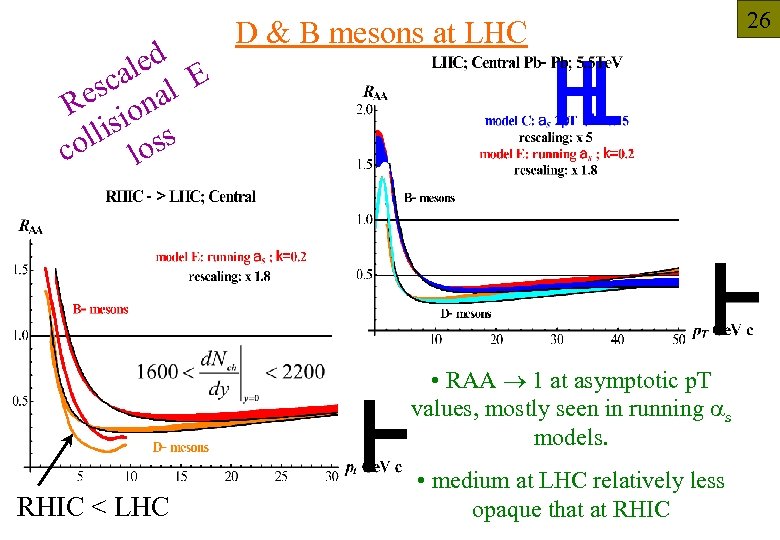 d ale l E sc a Re ion llis oss co l D & B mesons at LHC • RAA 1 at asymptotic p. T values, mostly seen in running as models. RHIC < LHC • medium at LHC relatively less opaque that at RHIC 26
d ale l E sc a Re ion llis oss co l D & B mesons at LHC • RAA 1 at asymptotic p. T values, mostly seen in running as models. RHIC < LHC • medium at LHC relatively less opaque that at RHIC 26
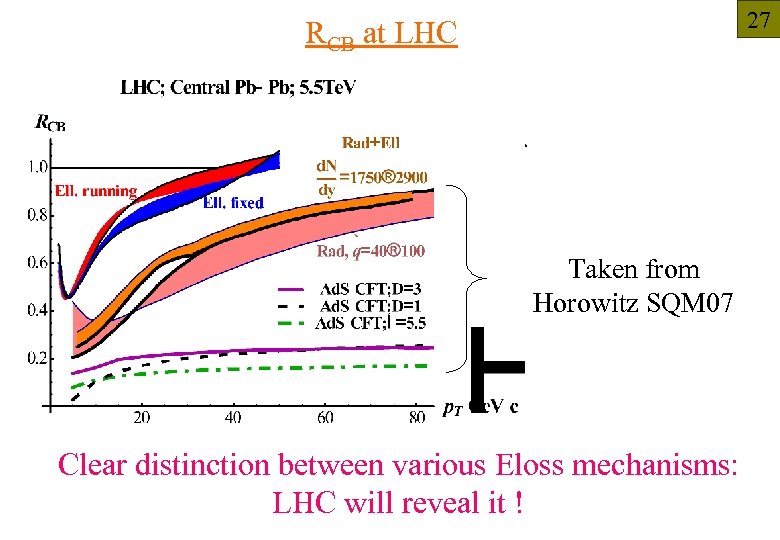 27 RCB at LHC Taken from Horowitz SQM 07 Clear distinction between various Eloss mechanisms: LHC will reveal it !
27 RCB at LHC Taken from Horowitz SQM 07 Clear distinction between various Eloss mechanisms: LHC will reveal it !
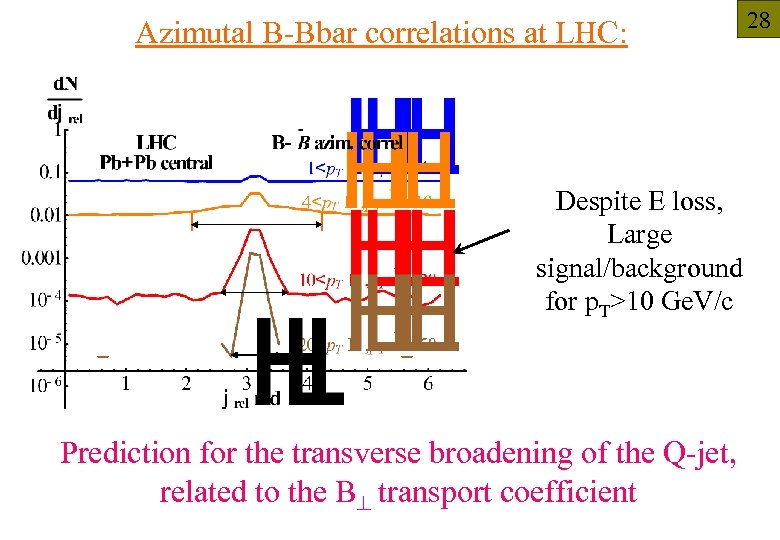 Azimutal B-Bbar correlations at LHC: 28 Despite E loss, Large signal/background for p. T>10 Ge. V/c Prediction for the transverse broadening of the Q-jet, related to the B transport coefficient
Azimutal B-Bbar correlations at LHC: 28 Despite E loss, Large signal/background for p. T>10 Ge. V/c Prediction for the transverse broadening of the Q-jet, related to the B transport coefficient
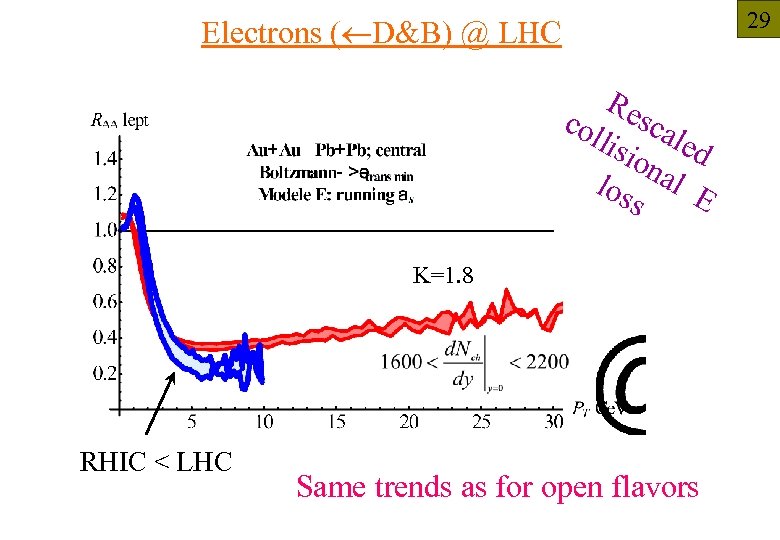 29 Electrons ( D&B) @ LHC Re col sca lisi led on los al E s K=1. 8 RHIC < LHC Same trends as for open flavors
29 Electrons ( D&B) @ LHC Re col sca lisi led on los al E s K=1. 8 RHIC < LHC Same trends as for open flavors
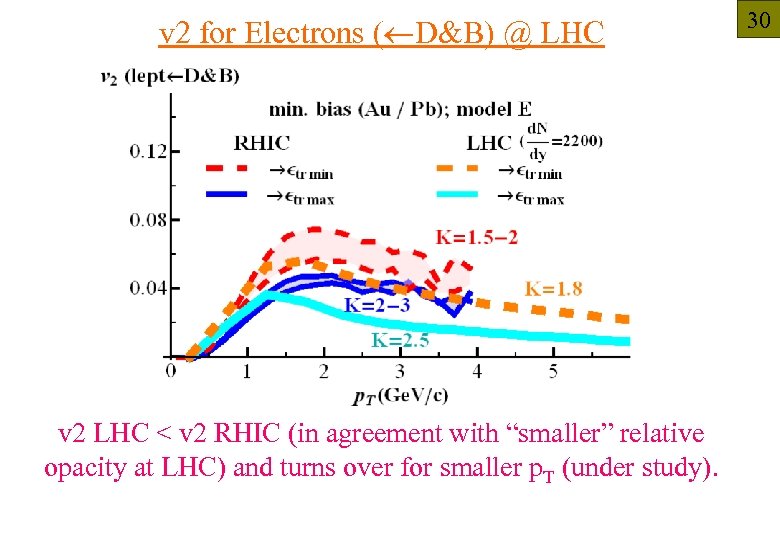 v 2 for Electrons ( D&B) @ LHC v 2 LHC < v 2 RHIC (in agreement with “smaller” relative opacity at LHC) and turns over for smaller p. T (under study). 30
v 2 for Electrons ( D&B) @ LHC v 2 LHC < v 2 RHIC (in agreement with “smaller” relative opacity at LHC) and turns over for smaller p. T (under study). 30
 Conclusions – Prospects: 31 I. One reproduces all known HQ observables at RHIC with Collisional energy loss rescaling factor of K=1. 5 -2 (<<20 with naïve model 1) on all p. T range provided one performs the evolution end of mixed phase II. Conservative predictions for LHC, found to be relatively less opaque than at RHIC, due to harder HQ initial distributions III. LHC will permit to distinguish between various E loss mechanisms (pure collisional, mixed rad + collisional, s. QGP Ad. S/CFT) IV. Q-Jet broadening in azimutal correlation will permit to test B transport coefficient and better constrains the medium. Need MC@NLO for better description of initial Q-production and e+ - e- correlations.
Conclusions – Prospects: 31 I. One reproduces all known HQ observables at RHIC with Collisional energy loss rescaling factor of K=1. 5 -2 (<<20 with naïve model 1) on all p. T range provided one performs the evolution end of mixed phase II. Conservative predictions for LHC, found to be relatively less opaque than at RHIC, due to harder HQ initial distributions III. LHC will permit to distinguish between various E loss mechanisms (pure collisional, mixed rad + collisional, s. QGP Ad. S/CFT) IV. Q-Jet broadening in azimutal correlation will permit to test B transport coefficient and better constrains the medium. Need MC@NLO for better description of initial Q-production and e+ - e- correlations.
 Back up
Back up
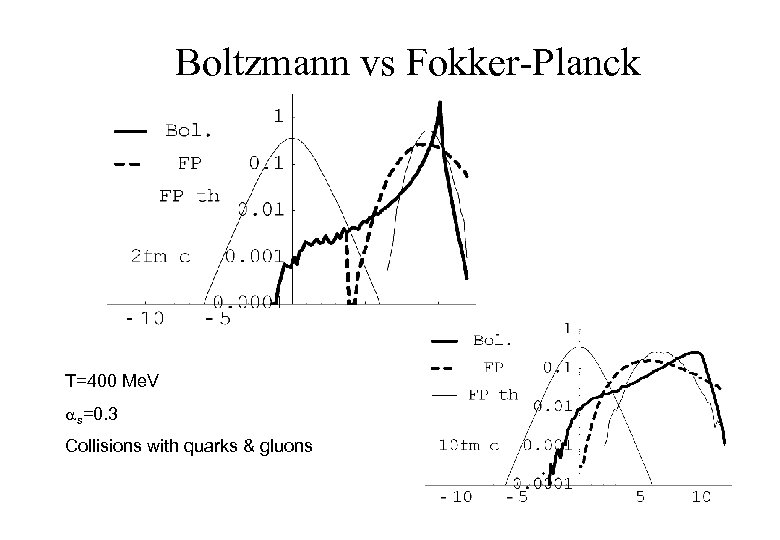 Boltzmann vs Fokker-Planck T=400 Me. V as=0. 3 Collisions with quarks & gluons
Boltzmann vs Fokker-Planck T=400 Me. V as=0. 3 Collisions with quarks & gluons
 Model B / 1
Model B / 1
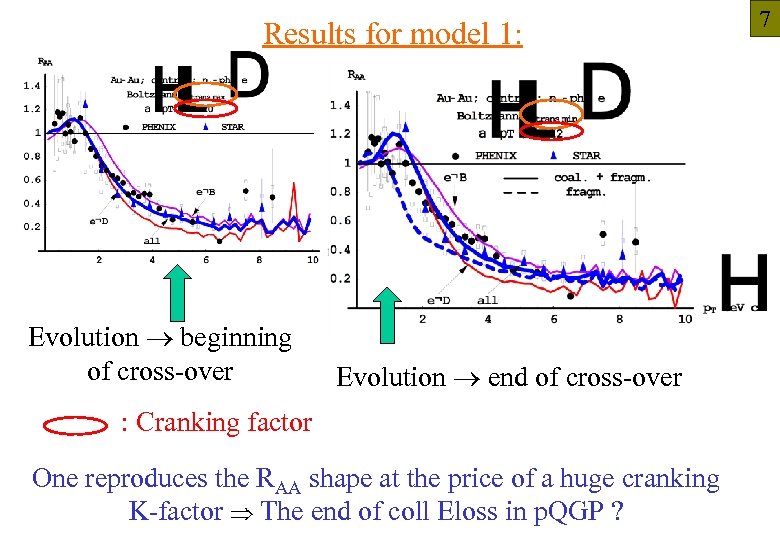 Results for model 1: Evolution beginning of cross-over Evolution end of cross-over : Cranking factor One reproduces the RAA shape at the price of a huge cranking K-factor The end of coll Eloss in p. QGP ? 7
Results for model 1: Evolution beginning of cross-over Evolution end of cross-over : Cranking factor One reproduces the RAA shape at the price of a huge cranking K-factor The end of coll Eloss in p. QGP ? 7
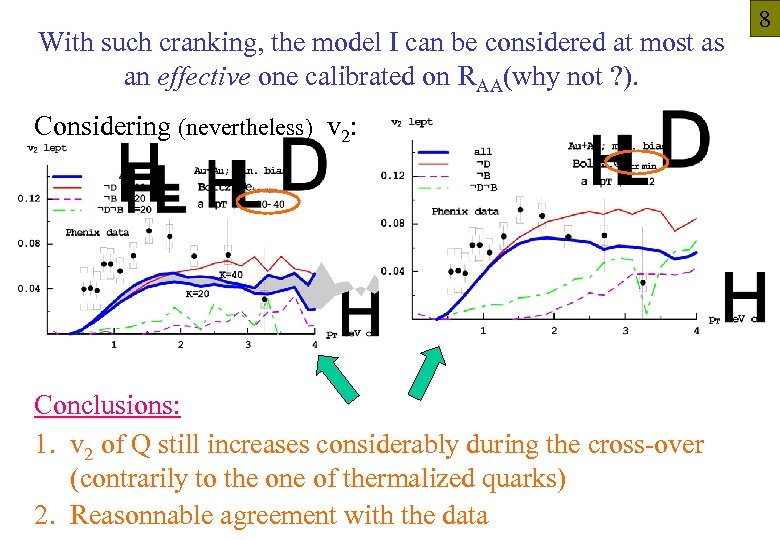 With such cranking, the model I can be considered at most as an effective one calibrated on RAA(why not ? ). Considering (nevertheless) v 2: Conclusions: 1. v 2 of Q still increases considerably during the cross-over (contrarily to the one of thermalized quarks) 2. Reasonnable agreement with the data 8
With such cranking, the model I can be considered at most as an effective one calibrated on RAA(why not ? ). Considering (nevertheless) v 2: Conclusions: 1. v 2 of Q still increases considerably during the cross-over (contrarily to the one of thermalized quarks) 2. Reasonnable agreement with the data 8
 Model C / 2
Model C / 2
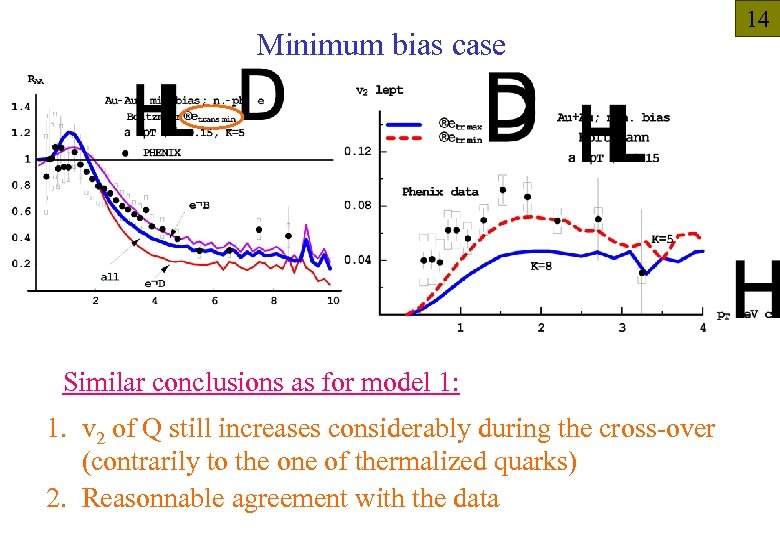 Minimum bias case Similar conclusions as for model 1: 1. v 2 of Q still increases considerably during the cross-over (contrarily to the one of thermalized quarks) 2. Reasonnable agreement with the data 14
Minimum bias case Similar conclusions as for model 1: 1. v 2 of Q still increases considerably during the cross-over (contrarily to the one of thermalized quarks) 2. Reasonnable agreement with the data 14
 Model E / 4
Model E / 4
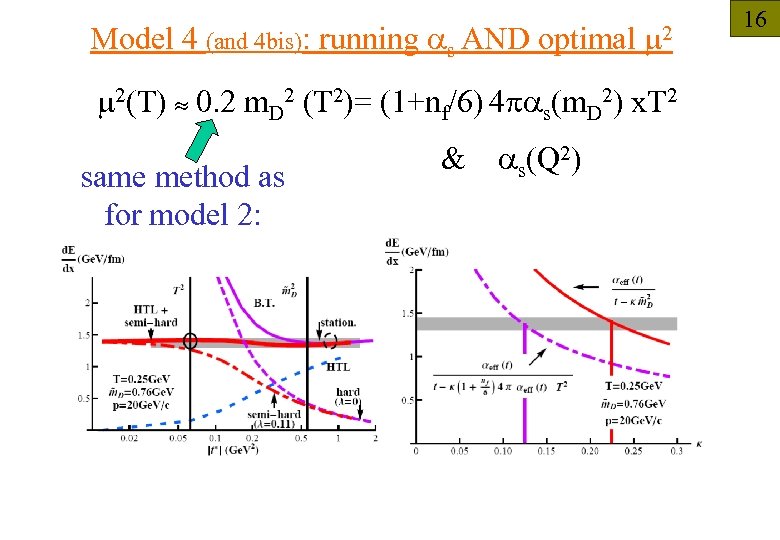 Model 4 (and 4 bis): running as AND optimal m 2(T) 0. 2 m. D 2 (T 2)= (1+nf/6) 4 pas(m. D 2) x. T 2 same method as for model 2: & as(Q 2) 16
Model 4 (and 4 bis): running as AND optimal m 2(T) 0. 2 m. D 2 (T 2)= (1+nf/6) 4 pas(m. D 2) x. T 2 same method as for model 2: & as(Q 2) 16
 Mesoscopic aspects of the model
Mesoscopic aspects of the model
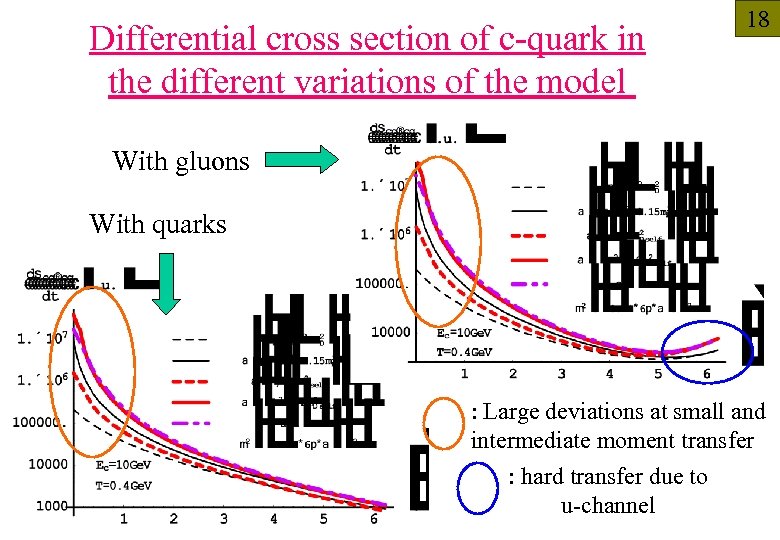 Differential cross section of c-quark in the different variations of the model 18 With gluons With quarks : Large deviations at small and intermediate moment transfer : hard transfer due to u-channel
Differential cross section of c-quark in the different variations of the model 18 With gluons With quarks : Large deviations at small and intermediate moment transfer : hard transfer due to u-channel
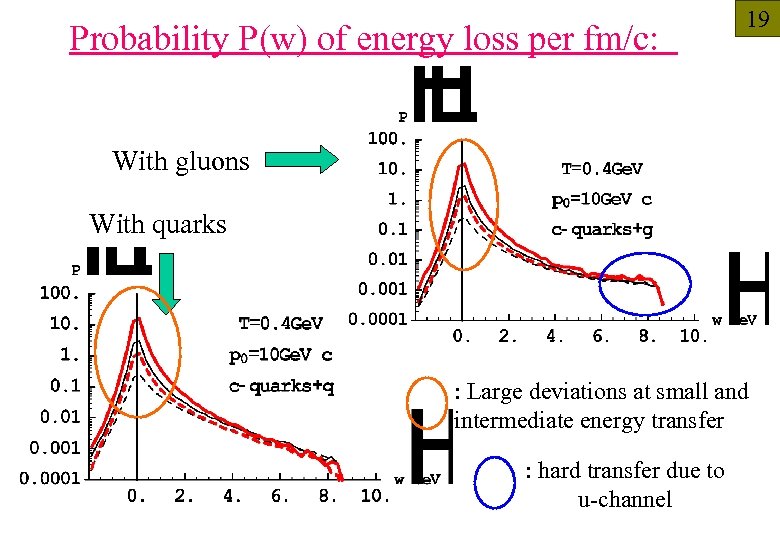 Probability P(w) of energy loss per fm/c: 19 With gluons With quarks : Large deviations at small and intermediate energy transfer : hard transfer due to u-channel
Probability P(w) of energy loss per fm/c: 19 With gluons With quarks : Large deviations at small and intermediate energy transfer : hard transfer due to u-channel
 v 2
v 2
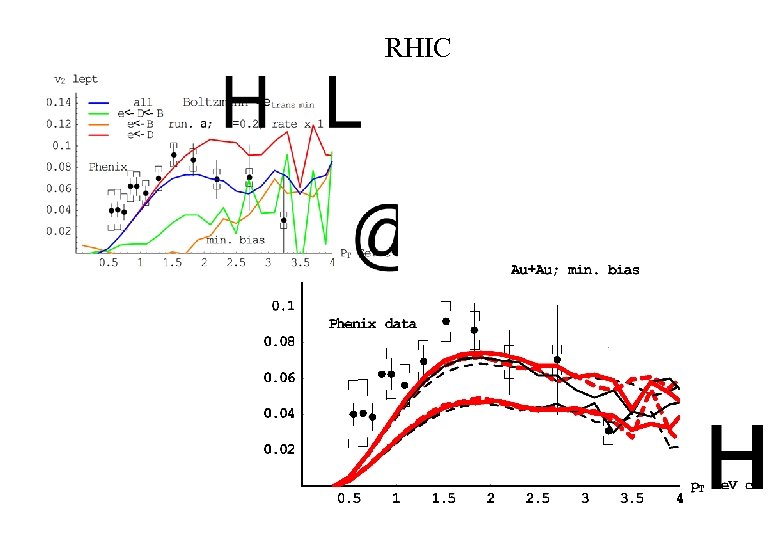 RHIC
RHIC
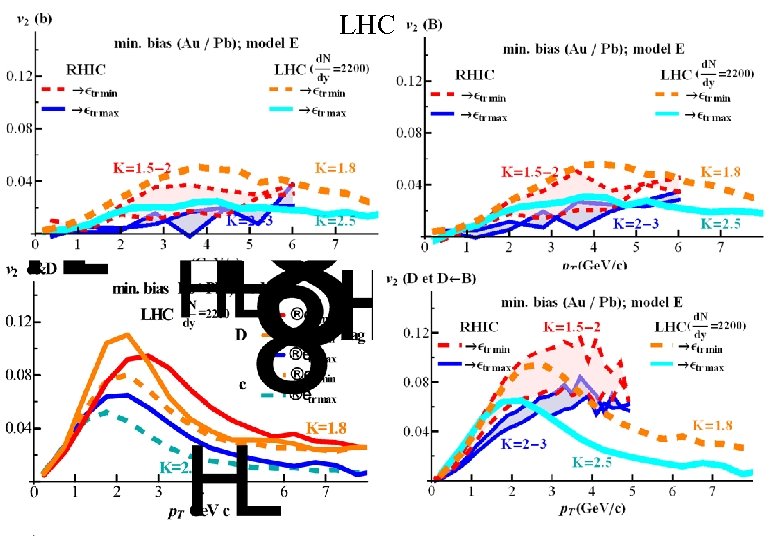 LHC
LHC
 RCB
RCB
 Looking for a Robust, Detectable Signal – Use LHC’s large p. T reach and identification of c and b to distinguish • RAA ~ (1 -e(p. T))n(p. T), where pf = (1 -e)pi (i. e. e = 1 -pf/pi) • Asymptotic p. QCD momentum loss: erad ~ as L 2 log(p. T/Mq)/p. T • String theory drag momentum loss: e. ST ~ 1 - Exp(-m L), m = pl 1/2 T 2/2 Mq S. Gubser, Phys. Rev. D 74: 126005 (2006); C. Herzog et al. JHEP 0607: 013, 2006 – Independent of p. T and strongly dependent on Mq! – T 2 dependence in exponent makes for a very sensitive probe – Expect: ep. QCD 0 vs. e. Ad. S indep of p. T!! • d. RAA(p. T)/dp. T > 0 => p. QCD; d. RAA(p. T)/dp. T < 0 => ST
Looking for a Robust, Detectable Signal – Use LHC’s large p. T reach and identification of c and b to distinguish • RAA ~ (1 -e(p. T))n(p. T), where pf = (1 -e)pi (i. e. e = 1 -pf/pi) • Asymptotic p. QCD momentum loss: erad ~ as L 2 log(p. T/Mq)/p. T • String theory drag momentum loss: e. ST ~ 1 - Exp(-m L), m = pl 1/2 T 2/2 Mq S. Gubser, Phys. Rev. D 74: 126005 (2006); C. Herzog et al. JHEP 0607: 013, 2006 – Independent of p. T and strongly dependent on Mq! – T 2 dependence in exponent makes for a very sensitive probe – Expect: ep. QCD 0 vs. e. Ad. S indep of p. T!! • d. RAA(p. T)/dp. T > 0 => p. QCD; d. RAA(p. T)/dp. T < 0 => ST


