How to Conceptualize and Value Earnings Growth Jim

How to Conceptualize and Value Earnings Growth Jim Ohlson Stern School of Business New York University August 2008

Key Result A formula (“OJ”) that expresses value in terms of next year expected EPS and growth in EPS Model Variables: Value depends on n EPS 1: Next-year expected EPS or “forward EPS”. n Year 2 vs. Year 1 growth (STG) in expected EPS n Some measure of long-term growth (LTG) in expected EPS n Discount factor which reflects risk (Cost of Equity Capital) P 0 EPS 1 EPS 2 LTG 2

Compelling Empirical Realities n n P 0 / EPS 1 correlates with short-term growth in EPS, but by no means perfectly P 0 / EPS 1 rates often exceed any reasonable estimate of the inverse of the cost of capital Short-term growth in EPS often substantially exceeds any reasonable estimate of cost of capital (e. g. , Google’s growth in estimated 2008 EPS vs. 2008 EPS is 28%) Analysts typically expect that superior EPS growth rates revert to “normal” rates over time 3

Implications of Empirical Realities The Constant (Gordon) Growth Model works only if cost of capital exceeds the perpetual growth rate. n One must model a decaying growth rate in EPS when short-term growth is relatively large. n 4

Approach to Assumptions n n Short-term growth (EPS 2 vs. EPS 1 adjusted for DPS 1) -- decays gradually to a steady state growth also determines the rate of decay in EPS growth. n P 0 equals the present value of expected DPS using the discount factor r (cost of equity capital). n Assumptions build in dividend policy irrelevancy. 5

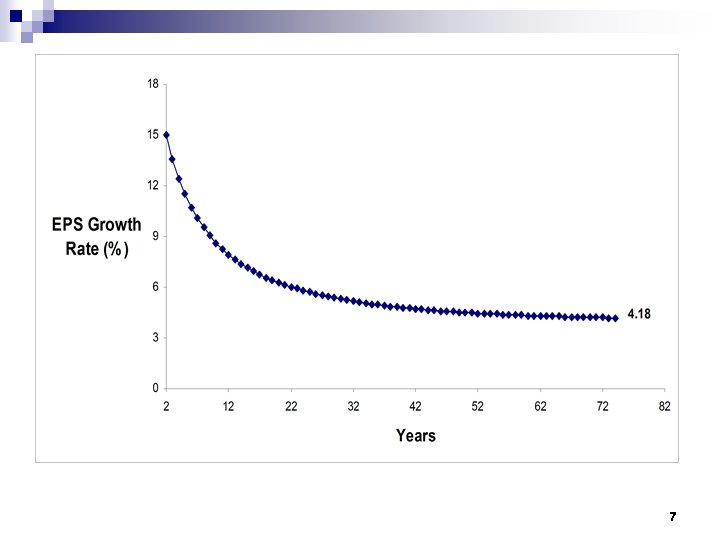
A Hypothetical Example Model Dynamics: Assuming full payout: Numerical illustration: These assumptions imply the following growth pattern. 6

7

n More generally, the model is determined by where r = cost of equity capital (8%, say) n does NOT depend on the dividend policy! 8

Basic Valuation Formula r = cost of equity capital = long-term EPS growth given full payout = as arguably approximates steady state growth in GNP 9

Example: GE Adjustments for dividends; If and then 10

Example: GE Does estimated value exceed actual price because our specification of r is too low? Try is evidently sensitive to r 11

Reverse Engineering: Infer r Familiar Problem: Estimates of intrinsic values are very sensitive to choice of discount factor n A More Sensible Approach: Solve for r given EPS 1/P 0, gs, and g. L. Leads to square-root formula: n 12

Reverse Engineering: Infer r n In the case of GE, 13

Comparative analysis r as P 0 r as gs or or EPS 1 g. L If g. L = 0 implies where PEG is “Price-to-Earnings divided by Growth”: 14

Very popular as a buy/sell signal, given risk is not a problem. n If two firms have the same and then the firm with the higher P 0 / EPS 1 ratio has lower risk. n 15

What Factors Should Determine r? In theory: r equals expected return, which depends upon risk (e. g. , CAPM b). In practice, r may be affected by the following: n Broader perceptions about equity risk n Market is expecting EPS 1 (and/or EPS 2) will soon be revised. n A high r implies an expected downward revision in EPS, and vice versa. n Mispricing 16

Can we say some about Why not assume Risk (premium) and growth are now two sides of the same coin 17

Empirical Evidence Do firm-specific measures of risk explain r using the square-root formula? Empirical question has been addressed for US data Assume all firms have the same (4%). r is regressed on the following variables: ¨ Beta ¨ Unsystematic risk ¨ Debt/Equity ¨ Earnings variability ¨ Long term growth per analyst estimate ¨ Book-to-Market ¨ Industry mean risk premium 18

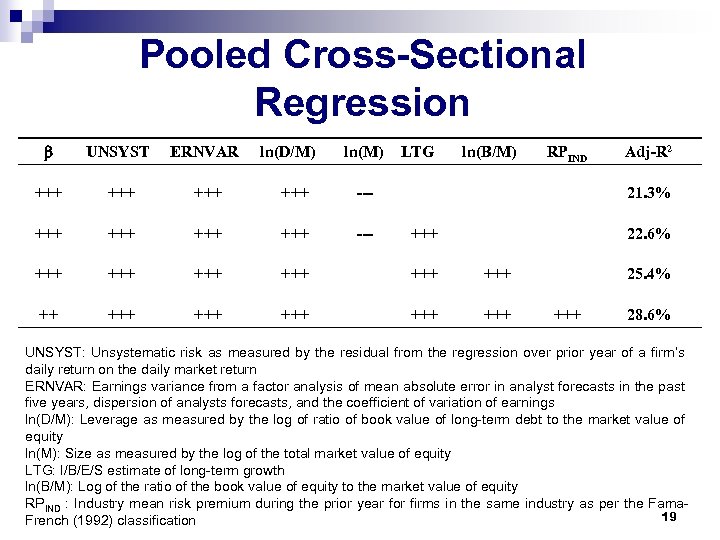Pooled Cross-Sectional Regression UNSYST ERNVAR +++ +++ --- +++ +++ +++ +++ ln(D/M) ln(M) LTG ln(B/M) RPIND Adj-R 2 21. 3% +++ 22. 6% 25. 4% +++ 28. 6% UNSYST: Unsystematic risk as measured by the residual from the regression over prior year of a firm’s daily return on the daily market return ERNVAR: Earnings variance from a factor analysis of mean absolute error in analyst forecasts in the past five years, dispersion of analysts forecasts, and the coefficient of variation of earnings ln(D/M): Leverage as measured by the log of ratio of book value of long-term debt to the market value of equity ln(M): Size as measured by the log of the total market value of equity LTG: I/B/E/S estimate of long-term growth ln(B/M): Log of the ratio of the book value of equity to the market value of equity RPIND : Industry mean risk premium during the prior year for firms in the same industry as per the Fama 19 French (1992) classification

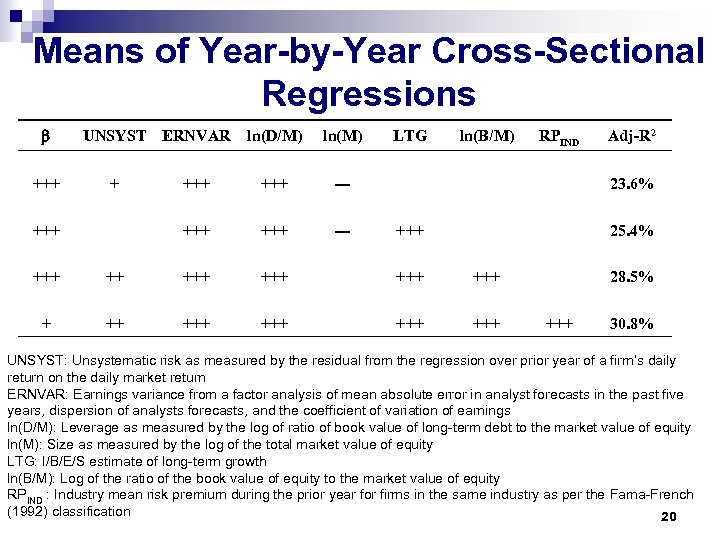Means of Year-by-Year Cross-Sectional Regressions +++ UNSYST ERNVAR +++ ln(M) +++ --- +++ + ln(D/M) +++ --- LTG ln(B/M) RPIND Adj-R 2 23. 6% +++ 25. 4% +++ +++ +++ +++ 28. 5% +++ 30. 8% UNSYST: Unsystematic risk as measured by the residual from the regression over prior year of a firm’s daily return on the daily market return ERNVAR: Earnings variance from a factor analysis of mean absolute error in analyst forecasts in the past five years, dispersion of analysts forecasts, and the coefficient of variation of earnings ln(D/M): Leverage as measured by the log of ratio of book value of long-term debt to the market value of equity ln(M): Size as measured by the log of the total market value of equity LTG: I/B/E/S estimate of long-term growth ln(B/M): Log of the ratio of the book value of equity to the market value of equity RPIND : Industry mean risk premium during the prior year for firms in the same industry as per the Fama-French (1992) classification 20

Summary n n Instead of using a constant growth assumption, we derive a simple formula expressing as a function of four variables: (i) next year estimated EPS (ii) short term EPS growth (iii) long term EPS growth (iv) cost of capital. The valuation formula is easy to implement using analysts’ forecasts. The “square-root” formula expresses the market’s assessment of a firm’s cost of capital; it depends only on (i) P 0 / EPS 1, and (ii), and (iii) Inferred cost of capital (r) are explained by (i) risk (ii) misleading “consensus” estimates of EPS 1 and , (iii) market inefficiencies. 21