9d57478d3d09b645312fe4f906f99aa9.ppt
- Количество слайдов: 56
 How Molecules Conduct Introduction to electron transport in molecular systems Reviews: Annu. Rev. Phys. Chem. 52, 681– 750 (2001) [http: //atto. tau. ac. il/~nitzan/nitzanabs. html/#213] Science, 300, 1384 -1389 (2003); MRS Bulletin, 29, 391 -395 (2004); Bulletin of the Israel Chemical Society, Issue 14, p. 3 -13 (Dec 2003) (Hebrew) Thanks I. Benjamin, A. Burin, B. Davis, S. Datta, D. Evans, M. Galperin, A. Ghosh, H. Grabert, P. Hänggi, G. Ingold, J. Jortner, S. Kohler, R. Kosloff, J. Lehmann, M. Majda, A. A. Mosyak, V. Mujica, R. Naaman, U. © Nitzan, TAU Peskin, M. Ratner, D. Segal, T. Seideman, H. Tal-Ezer
How Molecules Conduct Introduction to electron transport in molecular systems Reviews: Annu. Rev. Phys. Chem. 52, 681– 750 (2001) [http: //atto. tau. ac. il/~nitzan/nitzanabs. html/#213] Science, 300, 1384 -1389 (2003); MRS Bulletin, 29, 391 -395 (2004); Bulletin of the Israel Chemical Society, Issue 14, p. 3 -13 (Dec 2003) (Hebrew) Thanks I. Benjamin, A. Burin, B. Davis, S. Datta, D. Evans, M. Galperin, A. Ghosh, H. Grabert, P. Hänggi, G. Ingold, J. Jortner, S. Kohler, R. Kosloff, J. Lehmann, M. Majda, A. A. Mosyak, V. Mujica, R. Naaman, U. © Nitzan, TAU Peskin, M. Ratner, D. Segal, T. Seideman, H. Tal-Ezer
 A. Nitzan Part A INTRODUCTION © A. Nitzan, TAU
A. Nitzan Part A INTRODUCTION © A. Nitzan, TAU
 Molecules as conductors © A. Nitzan, TAU
Molecules as conductors © A. Nitzan, TAU
 Molecular Rectifiers Aviram Ratner Arieh Aviram and Mark A. Ratner IBM Thomas J. Watson Research Center, Yorktown Heights, New York 10598, USA Department of Chemistry, New York University, New York 10003, USA Received 10 June 1974 Abstract The construction of a very simple electronic device, a rectifier, based on the use of a single organic molecule is discussed. The molecular rectifier consists of a donor pi system and an acceptor pi system, separated by a sigmabonded (methylene) tunnelling bridge. The response of such a molecule to an applied field is calculated, and rectifier properties indeed appear. © A. Nitzan, TAU
Molecular Rectifiers Aviram Ratner Arieh Aviram and Mark A. Ratner IBM Thomas J. Watson Research Center, Yorktown Heights, New York 10598, USA Department of Chemistry, New York University, New York 10003, USA Received 10 June 1974 Abstract The construction of a very simple electronic device, a rectifier, based on the use of a single organic molecule is discussed. The molecular rectifier consists of a donor pi system and an acceptor pi system, separated by a sigmabonded (methylene) tunnelling bridge. The response of such a molecule to an applied field is calculated, and rectifier properties indeed appear. © A. Nitzan, TAU
 Xe on Ni(110) © A. Nitzan, TAU
Xe on Ni(110) © A. Nitzan, TAU
 Feynman © A. Nitzan, TAU Chad Mirkin (DPN)
Feynman © A. Nitzan, TAU Chad Mirkin (DPN)
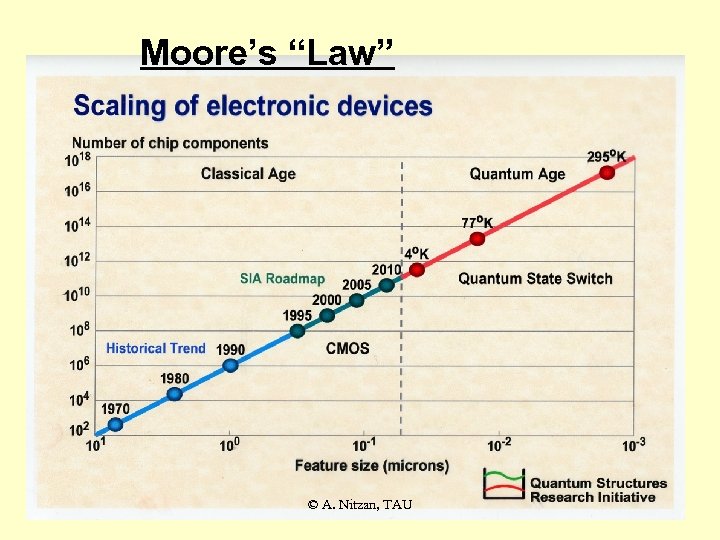 Moore’s “Law” © A. Nitzan, TAU
Moore’s “Law” © A. Nitzan, TAU
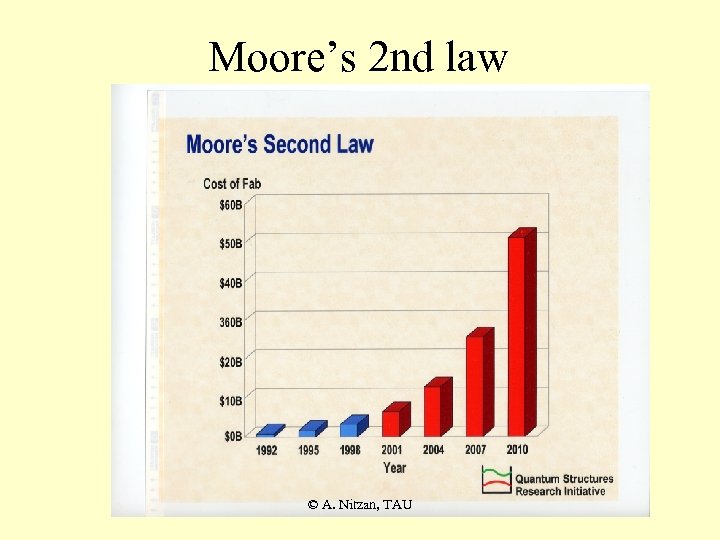 Moore’s 2 nd law © A. Nitzan, TAU
Moore’s 2 nd law © A. Nitzan, TAU
 Molecules get wired © A. Nitzan, TAU
Molecules get wired © A. Nitzan, TAU
 © A. Nitzan, TAU Cornell group
© A. Nitzan, TAU Cornell group
 © A. Nitzan, TAU
© A. Nitzan, TAU
 http: //www. hemdweb. co/ April 2002 © A. Nitzan, TAU
http: //www. hemdweb. co/ April 2002 © A. Nitzan, TAU
 The Hedonistic Imperative outlines how genetic engineering and nanotechnology will abolish suffering in all sentient life. The abolitionist project is hugely ambitious but technically feasible. It is also instrumentally rational and ethically mandatory. The metabolic pathways of pain and malaise evolved because they served the fitness of our genes in the ancestral environment. They will be replaced by a different sort of neural architecture. States of sublime well-being are destined to become the genetically pre-programmed norm of mental health. The world's last unpleasant experience will be a © A. Nitzan, precisely dateable event. TAU
The Hedonistic Imperative outlines how genetic engineering and nanotechnology will abolish suffering in all sentient life. The abolitionist project is hugely ambitious but technically feasible. It is also instrumentally rational and ethically mandatory. The metabolic pathways of pain and malaise evolved because they served the fitness of our genes in the ancestral environment. They will be replaced by a different sort of neural architecture. States of sublime well-being are destined to become the genetically pre-programmed norm of mental health. The world's last unpleasant experience will be a © A. Nitzan, precisely dateable event. TAU
 © A. Nitzan, TAU
© A. Nitzan, TAU
 Feynman • For a successful Technology, reality must take precedence over public relations, for nature cannot be fooled © A. Nitzan, TAU
Feynman • For a successful Technology, reality must take precedence over public relations, for nature cannot be fooled © A. Nitzan, TAU
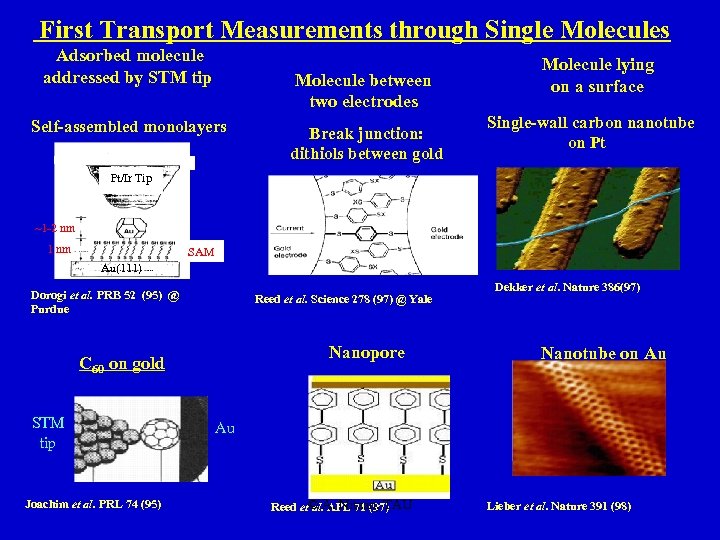 First Transport Measurements through Single Molecules Adsorbed molecule addressed by STM tip Molecule between two electrodes Self-assembled monolayers Break junction: dithiols between gold Molecule lying on a surface Single-wall carbon nanotube on Pt Pt/Ir Tip ~1 -2 nm 1 nm SAM Au(111) Dorogi et al. PRB 52 (95) @ Purdue Reed et al. Science 278 (97) @ Yale Nanopore C 60 on gold STM tip Joachim et al. PRL 74 (95) Dekker et al. Nature 386(97) Nanotube on Au Au Reed et© A. Nitzan, TAU al. APL 71 (97) Lieber et al. Nature 391 (98)
First Transport Measurements through Single Molecules Adsorbed molecule addressed by STM tip Molecule between two electrodes Self-assembled monolayers Break junction: dithiols between gold Molecule lying on a surface Single-wall carbon nanotube on Pt Pt/Ir Tip ~1 -2 nm 1 nm SAM Au(111) Dorogi et al. PRB 52 (95) @ Purdue Reed et al. Science 278 (97) @ Yale Nanopore C 60 on gold STM tip Joachim et al. PRL 74 (95) Dekker et al. Nature 386(97) Nanotube on Au Au Reed et© A. Nitzan, TAU al. APL 71 (97) Lieber et al. Nature 391 (98)
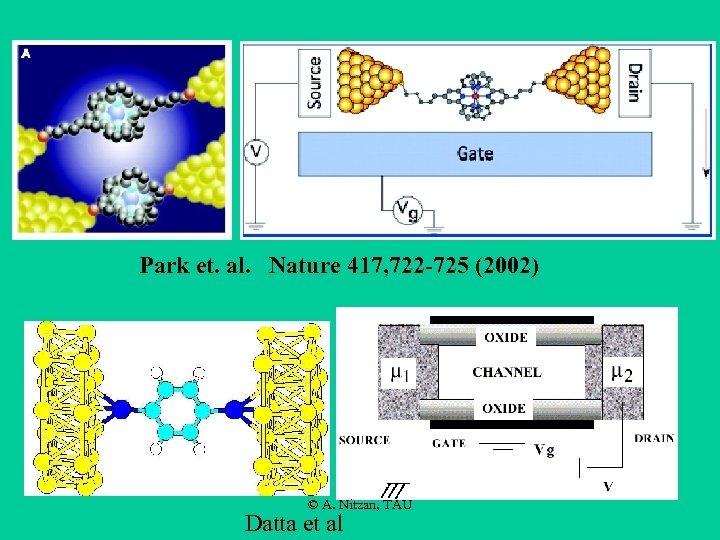 Park et. al. Nature 417, 722 -725 (2002) © A. Nitzan, TAU Datta et al
Park et. al. Nature 417, 722 -725 (2002) © A. Nitzan, TAU Datta et al
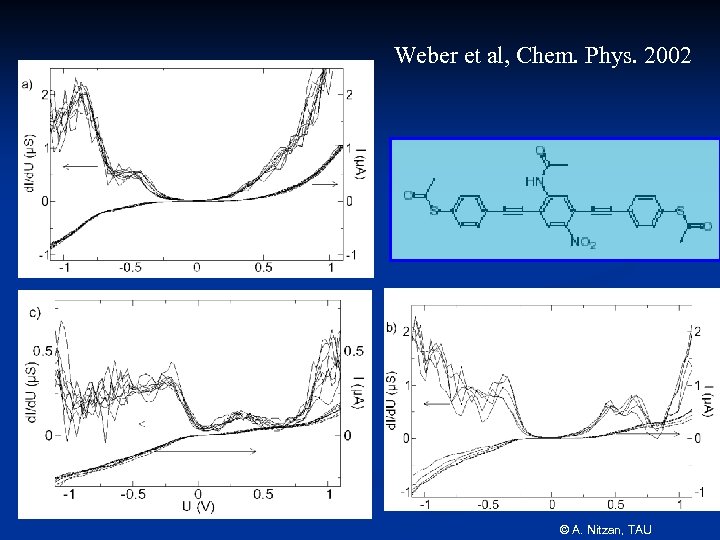 Weber et al, Chem. Phys. 2002 © A. Nitzan, TAU
Weber et al, Chem. Phys. 2002 © A. Nitzan, TAU
 Electron transfer in DNA © A. Nitzan, TAU
Electron transfer in DNA © A. Nitzan, TAU
 Electronic processes in molecular systems Electron transfer n Electron transmission n Conduction n Parameters that affect molecular conduction n Eleastic and inelastic transmission n Coherent and incoherent conduction n Heating and heat conduction n © A. Nitzan, TAU
Electronic processes in molecular systems Electron transfer n Electron transmission n Conduction n Parameters that affect molecular conduction n Eleastic and inelastic transmission n Coherent and incoherent conduction n Heating and heat conduction n © A. Nitzan, TAU
 Theory of Electron Transfer n n n n n The physics of activated rate process The physics of electron transfer in a nuclear environment A simple model – parabolic potential surfaces The Marcus parabolas The reorganization energy Adiabatic and non adiabatic rates Solvent control Bridge length dependence (“super-exchange”) Transition to hopping Experimental implications © A. Nitzan, TAU
Theory of Electron Transfer n n n n n The physics of activated rate process The physics of electron transfer in a nuclear environment A simple model – parabolic potential surfaces The Marcus parabolas The reorganization energy Adiabatic and non adiabatic rates Solvent control Bridge length dependence (“super-exchange”) Transition to hopping Experimental implications © A. Nitzan, TAU
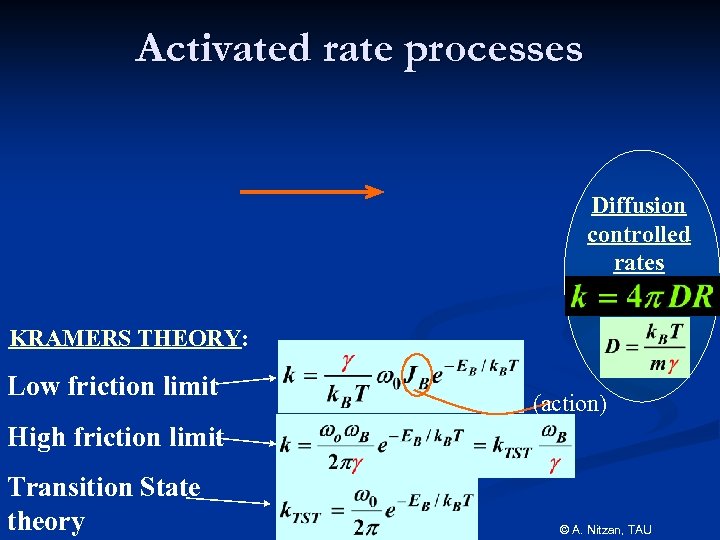 Activated rate processes Diffusion controlled rates KRAMERS THEORY: Low friction limit (action) High friction limit Transition State theory © A. Nitzan, TAU
Activated rate processes Diffusion controlled rates KRAMERS THEORY: Low friction limit (action) High friction limit Transition State theory © A. Nitzan, TAU
 The physics of transition state rates Assume: (1) Equilibrium in the well (2) Every trajectory on the barrier that goes out makes it © A. Nitzan, TAU
The physics of transition state rates Assume: (1) Equilibrium in the well (2) Every trajectory on the barrier that goes out makes it © A. Nitzan, TAU
 Electron transfer in polar media • Electron are much faster than nuclei • Electronic transitions take place in fixed nuclear configurations • Electronic energy needs to be conserved during the change in electronic charge density Electronic transition Nuclear relaxation © A. Nitzan, TAU
Electron transfer in polar media • Electron are much faster than nuclei • Electronic transitions take place in fixed nuclear configurations • Electronic energy needs to be conserved during the change in electronic charge density Electronic transition Nuclear relaxation © A. Nitzan, TAU
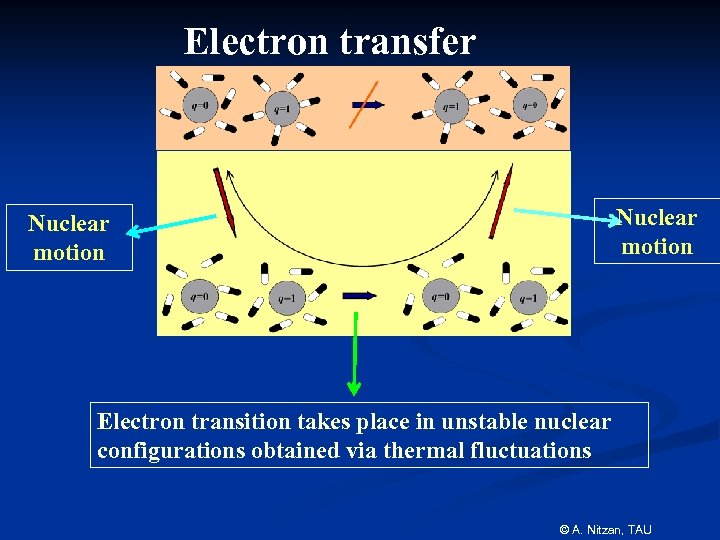 Electron transfer Nuclear motion Electron transition takes place in unstable nuclear configurations obtained via thermal fluctuations © A. Nitzan, TAU
Electron transfer Nuclear motion Electron transition takes place in unstable nuclear configurations obtained via thermal fluctuations © A. Nitzan, TAU
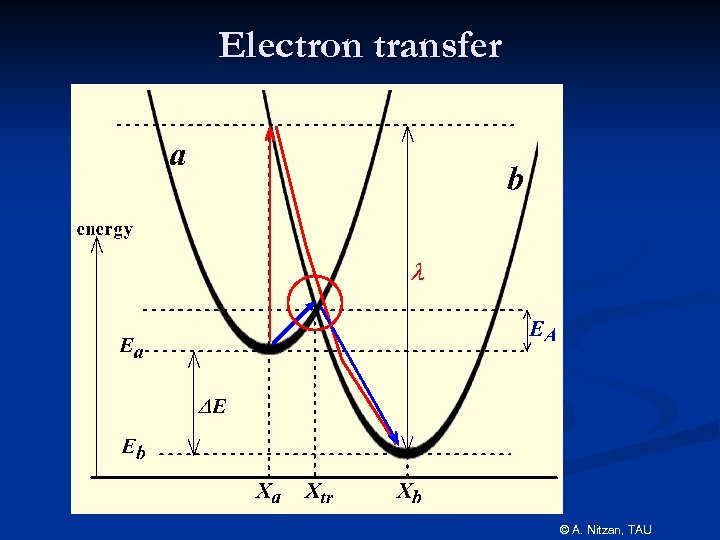 Electron transfer © A. Nitzan, TAU
Electron transfer © A. Nitzan, TAU
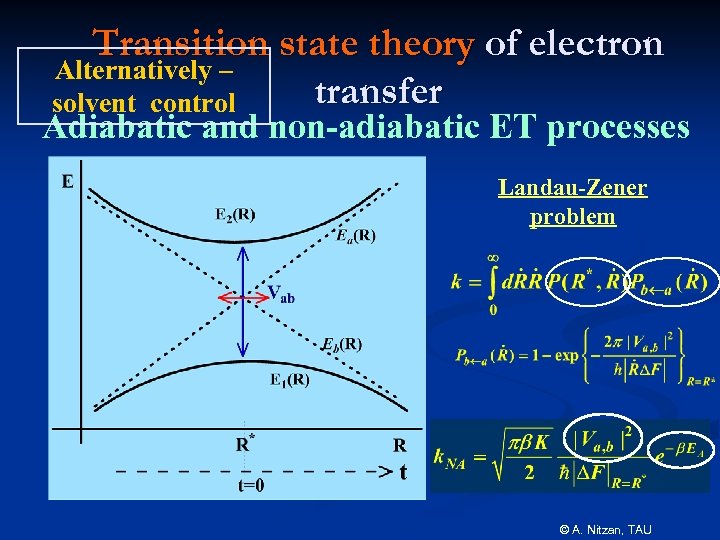 Transition state theory of electron Alternatively – transfer solvent control Adiabatic and non-adiabatic ET processes Landau-Zener problem © A. Nitzan, TAU
Transition state theory of electron Alternatively – transfer solvent control Adiabatic and non-adiabatic ET processes Landau-Zener problem © A. Nitzan, TAU
 Electron transfer – Marcus theory We are interested in changes in solvent configuration that take place at constant solute charge distribution They have the following characteristics: (1) Pn fluctuates because of thermal motion of solvent nuclei. (2) Pe , as a fast variable, satisfies the equilibrium relationship (3) D = constant (depends on only) Note that the relations E = D-4 P; P=Pn + Pe are always satisfied per definition, however D s. E. (the latter equality holds only at equilibrium). © A. Nitzan, TAU
Electron transfer – Marcus theory We are interested in changes in solvent configuration that take place at constant solute charge distribution They have the following characteristics: (1) Pn fluctuates because of thermal motion of solvent nuclei. (2) Pe , as a fast variable, satisfies the equilibrium relationship (3) D = constant (depends on only) Note that the relations E = D-4 P; P=Pn + Pe are always satisfied per definition, however D s. E. (the latter equality holds only at equilibrium). © A. Nitzan, TAU
 The Marcus parabolas Use q as a reaction coordinate. It defines the state of the medium that will be in equilibrium with the charge distribution rq. Marcus calculated the free energy (as function of q) of the solvent when it reaches this state in the systems q =0 and q=1. © A. Nitzan, TAU
The Marcus parabolas Use q as a reaction coordinate. It defines the state of the medium that will be in equilibrium with the charge distribution rq. Marcus calculated the free energy (as function of q) of the solvent when it reaches this state in the systems q =0 and q=1. © A. Nitzan, TAU
 Electron transfer: Activation energy © A. Nitzan, TAU
Electron transfer: Activation energy © A. Nitzan, TAU
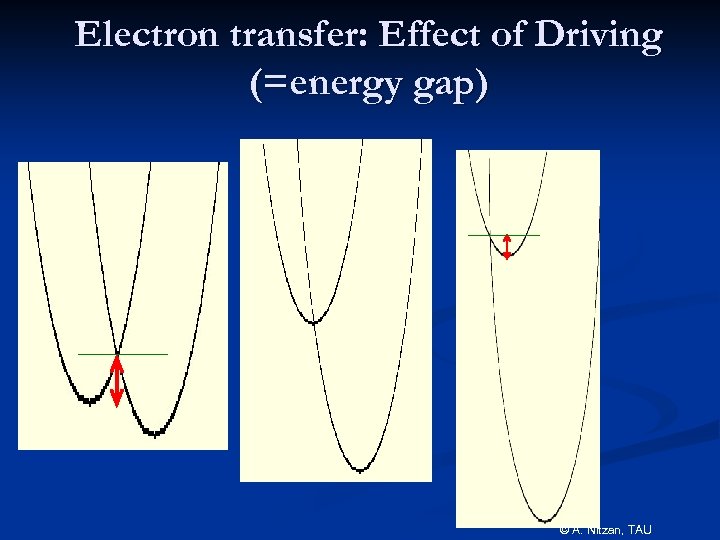 Electron transfer: Effect of Driving (=energy gap) © A. Nitzan, TAU
Electron transfer: Effect of Driving (=energy gap) © A. Nitzan, TAU
 Experimental confirmation of the inverted regime Miller et al, JACS(1984) Marcus Nobel Prize: 1992 © A. Nitzan, TAU
Experimental confirmation of the inverted regime Miller et al, JACS(1984) Marcus Nobel Prize: 1992 © A. Nitzan, TAU
 Electron transfer – the coupling • From Quantum Chemical Calculations • The Mulliken-Hush formula • Bridge mediated electron transfer © A. Nitzan, TAU
Electron transfer – the coupling • From Quantum Chemical Calculations • The Mulliken-Hush formula • Bridge mediated electron transfer © A. Nitzan, TAU
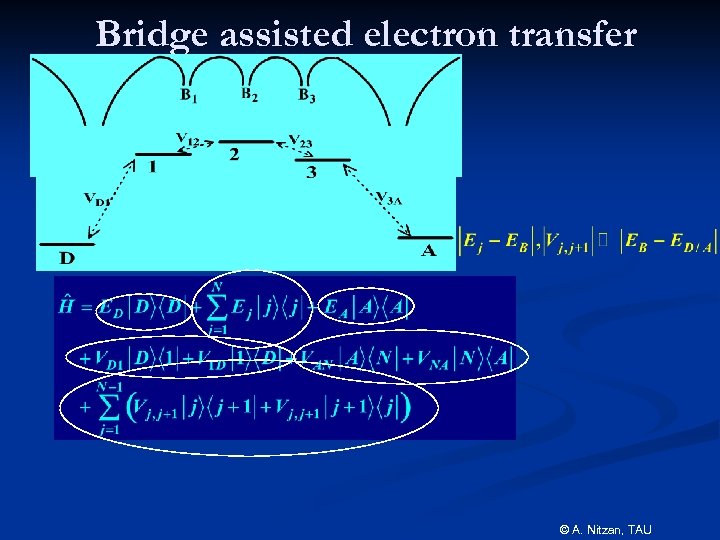 Bridge assisted electron transfer © A. Nitzan, TAU
Bridge assisted electron transfer © A. Nitzan, TAU
 BEWARE: equations are coming! © A. Nitzan, TAU
BEWARE: equations are coming! © A. Nitzan, TAU
 Effective donor-acceptor coupling © A. Nitzan, TAU
Effective donor-acceptor coupling © A. Nitzan, TAU
 Marcus expresions for non-adiabatic ET rates Donor-to-Bridge/ Acceptor-to-bridge Bridge Green’s Function Franck-Condonweighted DOS Reorganization energy © A. Nitzan, TAU
Marcus expresions for non-adiabatic ET rates Donor-to-Bridge/ Acceptor-to-bridge Bridge Green’s Function Franck-Condonweighted DOS Reorganization energy © A. Nitzan, TAU
 Bridge mediated ET rate b’ (Å-1)= 0. 2 -0. 6 for highly conjugated chains 0. 9 -1. 2 for saturated hydrocarbons ~2 for vacuum © A. Nitzan, TAU
Bridge mediated ET rate b’ (Å-1)= 0. 2 -0. 6 for highly conjugated chains 0. 9 -1. 2 for saturated hydrocarbons ~2 for vacuum © A. Nitzan, TAU
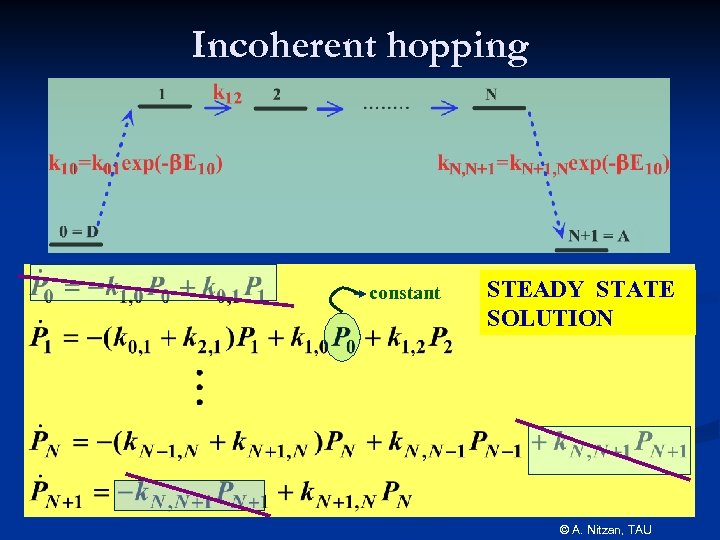 Incoherent hopping constant STEADY STATE SOLUTION © A. Nitzan, TAU
Incoherent hopping constant STEADY STATE SOLUTION © A. Nitzan, TAU
 ET rate from steady state hopping © A. Nitzan, TAU
ET rate from steady state hopping © A. Nitzan, TAU
 Dependence on temperature The integrated elastic (dotted line) and activated (dashed line) components of the transmission, and the total transmission probability (full line) displayed as function of inverse temperature. Parameters are as in Fig. 3. © A. Nitzan, TAU
Dependence on temperature The integrated elastic (dotted line) and activated (dashed line) components of the transmission, and the total transmission probability (full line) displayed as function of inverse temperature. Parameters are as in Fig. 3. © A. Nitzan, TAU
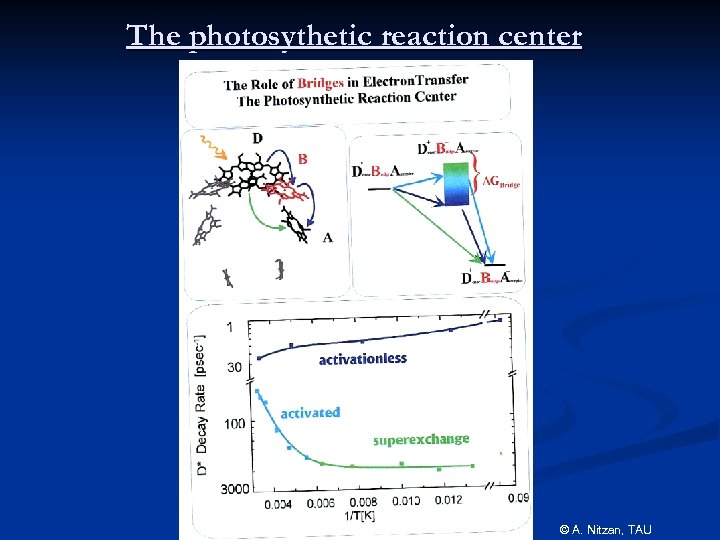 The photosythetic reaction center © A. Nitzan, TAU
The photosythetic reaction center © A. Nitzan, TAU
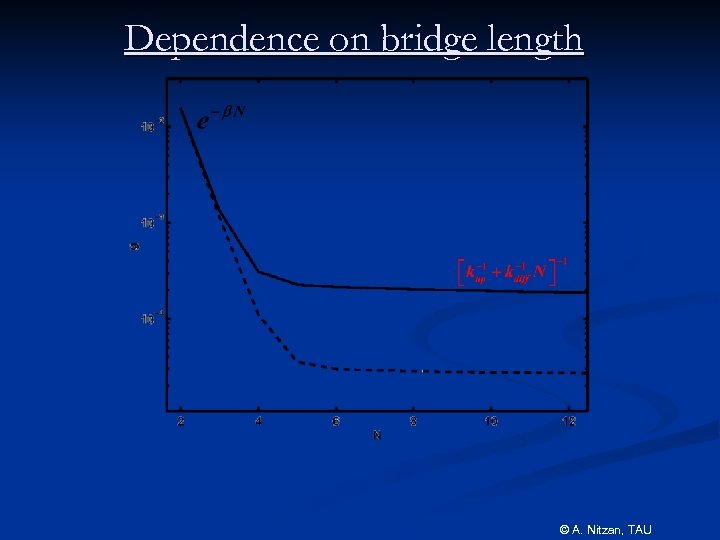 Dependence on bridge length © A. Nitzan, TAU
Dependence on bridge length © A. Nitzan, TAU
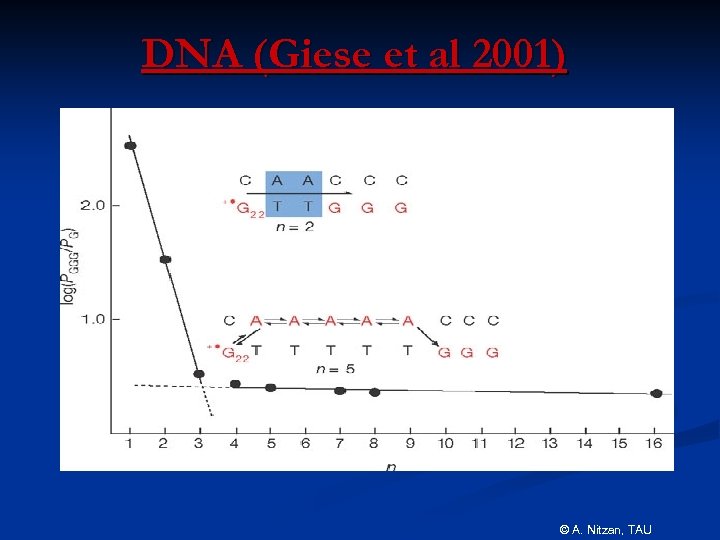 DNA (Giese et al 2001) © A. Nitzan, TAU
DNA (Giese et al 2001) © A. Nitzan, TAU
 Steady state evaluation of rates Rate of water flow depends linearly on water height in the cylinder h Two ways to get the rate of water flowing out: (1) Measure h(t) and get the rate coefficient from k=(1/h)dh/dt (2) Keep h constant and measure the steady state outwards water flux J. Get the rate from k=J/h -- Steady state rate © A. Nitzan, TAU
Steady state evaluation of rates Rate of water flow depends linearly on water height in the cylinder h Two ways to get the rate of water flowing out: (1) Measure h(t) and get the rate coefficient from k=(1/h)dh/dt (2) Keep h constant and measure the steady state outwards water flux J. Get the rate from k=J/h -- Steady state rate © A. Nitzan, TAU
 Steady state quantum mechanics Starting from state 0 at t=0: P 0 = exp(-G 0 t) V 0 l G = 2 |Vsl|2 L (Golden Rule) Steady state derivation: © A. Nitzan, TAU
Steady state quantum mechanics Starting from state 0 at t=0: P 0 = exp(-G 0 t) V 0 l G = 2 |Vsl|2 L (Golden Rule) Steady state derivation: © A. Nitzan, TAU
 pumping damping © A. Nitzan, TAU
pumping damping © A. Nitzan, TAU
 Resonance scattering V 1 l V 1 r © A. Nitzan, TAU
Resonance scattering V 1 l V 1 r © A. Nitzan, TAU
 Resonance scattering For each r and l j = 0, 1, {l}, {r} © A. Nitzan, TAU
Resonance scattering For each r and l j = 0, 1, {l}, {r} © A. Nitzan, TAU
 SELF ENERGY © A. Nitzan, TAU
SELF ENERGY © A. Nitzan, TAU
 © A. Nitzan, TAU
© A. Nitzan, TAU
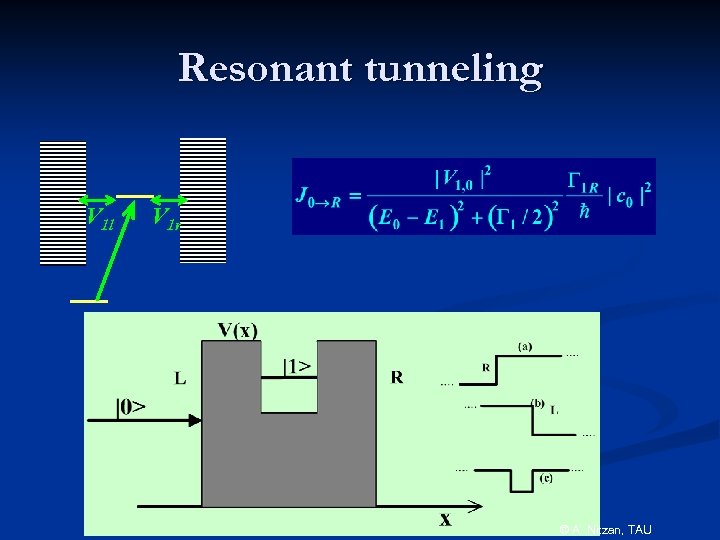 Resonant tunneling V 1 l V 1 r © A. Nitzan, TAU
Resonant tunneling V 1 l V 1 r © A. Nitzan, TAU
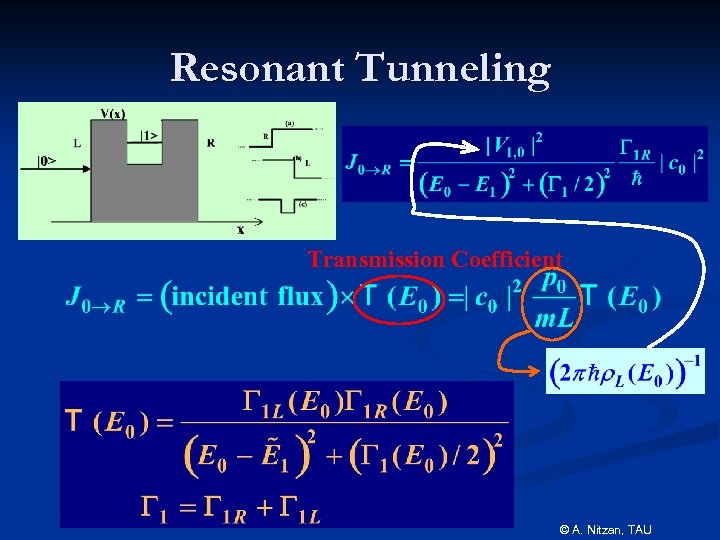 Resonant Tunneling Transmission Coefficient © A. Nitzan, TAU
Resonant Tunneling Transmission Coefficient © A. Nitzan, TAU
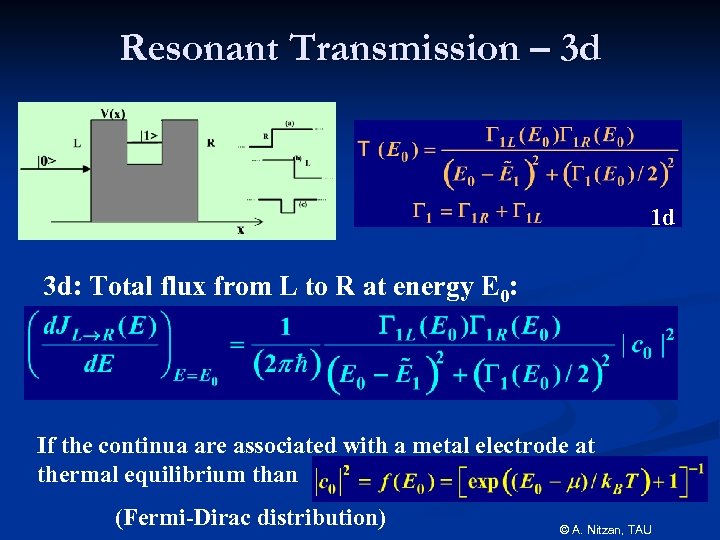 Resonant Transmission – 3 d 1 d 3 d: Total flux from L to R at energy E 0: If the continua are associated with a metal electrode at thermal equilibrium than (Fermi-Dirac distribution) © A. Nitzan, TAU
Resonant Transmission – 3 d 1 d 3 d: Total flux from L to R at energy E 0: If the continua are associated with a metal electrode at thermal equilibrium than (Fermi-Dirac distribution) © A. Nitzan, TAU
 CONDUCTION L R m – |e|f m f(E 0) (Fermi function) 2 spin states Zero bias conduction © A. Nitzan, TAU
CONDUCTION L R m – |e|f m f(E 0) (Fermi function) 2 spin states Zero bias conduction © A. Nitzan, TAU
 Landauer formula For a single “channel”: (maximum=1) Maximum conductance per channel © A. Nitzan, TAU
Landauer formula For a single “channel”: (maximum=1) Maximum conductance per channel © A. Nitzan, TAU


