4ede83aa6f8bdbcc6007522b35a2fdf6.ppt
- Количество слайдов: 56

Homework Problems Chapter 5 Homework Problems: 1, 12, 16, 18, 20, 28, 30, 36, 38, 40, 48, 50, 62, 66, 87, 96, 108, 122

CHAPTER 5 Thermochemistry
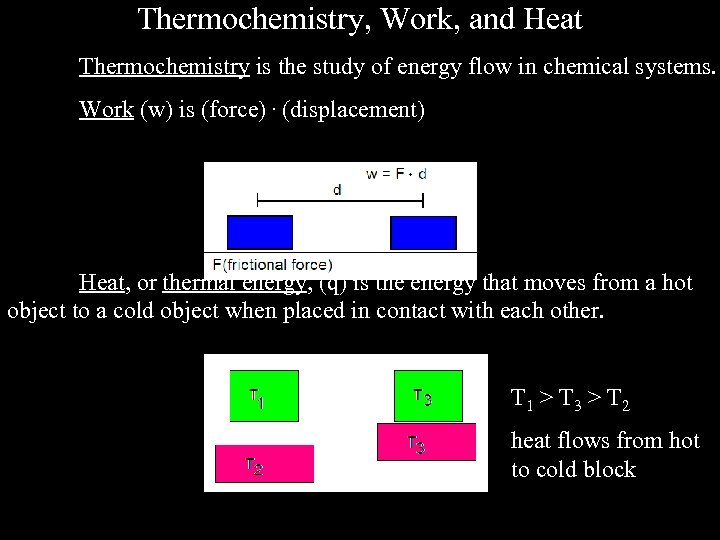
Thermochemistry, Work, and Heat Thermochemistry is the study of energy flow in chemical systems. Work (w) is (force). (displacement) Heat, or thermal energy, (q) is the energy that moves from a hot object to a cold object when placed in contact with each other. T 1 > T 3 > T 2 heat flows from hot to cold block

Energy

Units of Energy All forms of energy can be expressed in the same units. To find the MKS unit for energy, it is convenient to use the equation for kinetic energy. EK = 1/2 mv 2 So units are (kg) (m/s)2 = kg. m 2 = 1 Joule = 1 J s 2 Since 1 J is a small amount of energy, we often express energy in terms of k. J (kilojoule). 1 k. J = 1000. J Other common units for energy include: calorie (cal) Amount of heat needed to raise the temperature of 1 g of water by 1 C 1 cal = 4. 184 J (exact) 1 kcal = 1 food calorie = 1000 cal = 4184. J (exact)

Heat and Chemical Reactions Some chemical reactions release heat into their surroundings. Other reactions require that the surroundings provide heat so that the reaction can proceed. An exothermic reaction is a reaction that releases heat to the surroundings. Combustion reactions are one common type of exothermic reaction 2 H 2(g) + O 2(g) 2 H 2 O(l) releases 572. k. J of heat per mole of reaction An endothermic reaction takes up heat from the surroundings. 2 Hg. O(s) 2 Hg(l) + O 2(g) takes up 181. k. J of heat per mole of reaction By convention, q < 0 for an exothermic reaction, and q > 0 for an endothermic reaction.

System, Surroundings, and Universe e study. The surroundings are everything not included in the system. The universe is everything - system + surroundings. While in principle the surroundings are everything not included in the system, in practice we can usually focus on that part of the surroundings in the immediate vicinity of the system.

Open, Closed, and Isolated Systems can be divided into various categories based on how they interact with their surroundings. Open system - A system that can exchange both energy and mass with its surroundings. Closed system - A system that can exchange energy with its surroundings, but which cannot exchange mass with its surroundings. Isolated system - A system that cannot exchange either energy or mass with its surroundings.

State Function A state function is any function whose change in value depends only on the initial and final state of the system, but which is independent of the pathway used to go between them. The value for something that is not a state function depends not only on the initial and final state but also on the pathway used to travel between them. Altitude is a state function, distance traveled is not a state function. In thermodynamics, U is a state function, q and w are not state functions (in fact, they are not functions at all!)
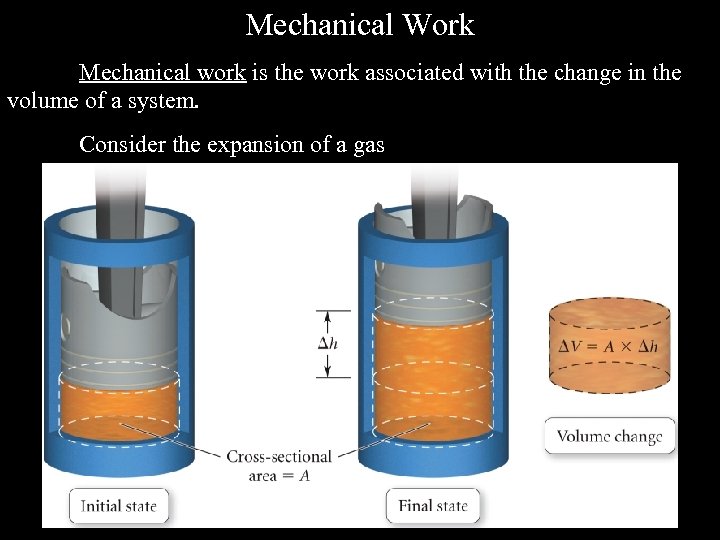
Mechanical Work Mechanical work is the work associated with the change in the volume of a system. Consider the expansion of a gas

Derivation of the Expression For Mechanical Work w = F. d (from the definition of work) But p = F/A, and so F = p. A So |w| = p. A. d However, from the diagram d = h So |w| = p. A. h But A. d = V where V is the change in volume. So |w| = p. V (absolute value) But notice that when a gas expands its volume change is in a direction opposite to that of the applied pressure. This introduces a negative sign into the expression for mechanical work. Therefore w = - p. V p d

First Law of Thermodynamics The first law of thermodynamics gives a relationship between internal energy, work, and heat. U = q + w U = Uf - Ui = change in internal energy q = heat w = work For now, we limit ourselves to mechanical work, where w = - p V. Note that the first law is based on experimental observation and is not derived from some other law or principle. The first law relates the change in a state function ( U) to the sum of two things that are not state functions (q and w).

Sign Convention for Heat and Work We use the following sign convention for heat and work. q > 0 heat flows from the surroundings into the system (endothermic) q < 0 heat flows from the system to the surroundings (exothermic) w > 0 work is done on the system (system is compressed) w < 0 work is done by the system (system expands) Note that qsur = - qsys, and wsur = - wsys.

Use of the First Law A gas is confined inside of a cylinder. The applied pressure is 1. 000 atm, and the initial volume occupied by the gas is 2. 000 L. 8000. J of heat is added to the gas under conditions of constant applied pressure. The final volume occupied by the gas is 6. 000 L. What are q, w, and U for the process?

A gas is confined inside of a cylinder. The applied pressure is 1. 000 atm, and the initial volume occupied by the gas is 2. 000 L. 8000. J of heat is added to the gas under conditions of constant applied pressure. The final volume occupied by the gas is 6. 000 L. What are q, w, and U for the process? From the first law, U = q + w. Heat is added to the system, so q = + 8000. J For constant pressure w = - p V = - (1. 00 atm) (6. 000 L – 2. 000 L) = - 4. 00 L. atm 101. 3 J = - 405. J * 1 L. atm Finally, U = q + w = 8000. J + (- 405. J) = 7595. J *Note: To find the conversion between L. atm and J we do the following # J = 1 L. atm 1 m 3 1. 013 x 105 N/m 2 = 101. 3 N. m = 101. 3 J 1000 L 1 atm

Constant Volume Processes Consider some general process taking place at constant volume. From the first law U = q + w But for mechanical work, w = - p V So at constant volume, V = 0, so w = 0 Therefore, for a process carried out at constant volume U = q. V (V = constant) What does this mean? For a process carried out at constant volume, q is a state function, and so no information is needed concerning path. This makes it far easier to calculate and keep track of heat flow for these kinds of processes.

Enthalpy Most processes in the laboratory are carried out at constant pressure instead of constant volume. It would be nice to have a state function whose change in value was equal to q for constant pressure processes. Enthalpy is such a function. We define enthalpy, H, as follows H = U + p. V Since U, p, and V are state functions, it follows that enthalpy is also a state function.

Constant Pressure Processes and Enthalpy Consider some general process taking place at constant pressure. From the definition of enthalpy H = U + p. V H = U + (p. V) = U + (pf. Vf - pi. Vi) Now, if pressure is held constant, then pf = pi = p, and so H = U + p(Vf - Vi) = U + p V Now, from the first law U = q + w If we only have mechanical work U = q - p V

If we now substitute into the expression for enthalpy, we get H = U + p V = (q - p V) + p V or (finally!) H = qp (p = constant) What does this mean? For a process carried out at constant pressure, q is a state function, and so no information is needed concerning path. This makes it far easier to calculate and keep track of heat flow for these kinds of processes. To summarize U = q. V (constant volume processes) H = qp (constant pressure processes) Since q is something that can be measured experimentally, we now have a way to relate this information to changes in state functions (internal energy or enthalpy).

Enthalpy of Reaction ( H rxn) Because of the importance of enthalpy, we define enthalpy changes for specific kinds of processes. H rxn (enthalpy of reaction) - The enthalpy change when one mole of a specific reaction is carried out at p = 1. 00 atm ( ); equals qp for the process. Example: Ca. CO 3(s) Ca. O(s) + CO 2(g) H rxn = + 178. 3 k. J/mol 2 Ca. CO 3(s) 2 Ca. O(s) + 2 CO 2(g) H rxn = + 356. 6 k. J/mol Ca. O(s) + CO 2(g) Ca. CO 3(s) H rxn = - 178. 3 k. J/mol Notice that multiplying a reaction by a constant multiplies the value for H rxn by the same constant. Changing the direction of a reaction changes the sign for H rxn.

We can see the last result as follows: Ca. CO 3(s) Ca. O(s) + CO 2(g) H rxn = + 178. 3 k. J/mol Ca. O(s) + CO 2(g) Ca. CO 3(s) H rxn = ? _____________________________ Ca. CO 3(s) H total = 0. 0 k. J/mol Carrying out the first process followed by the second process means that our final state is the same as our initial state. There is no change in the system, and so H total = 0. 0 k. J/mol. Therefore, the change in enthalpy for the second process must be the same as the change in enthalpy for the first process, except for the sign.

The Physical State of the Reactants and Products The value for the enthalpy change for a process depends not only on the identity and amounts of the reactants and products but also their state. Consider the following example: 2 H 2(g) + O 2(g) 2 H 2 O(l) H rxn = - 571. 6 k. J/mol 2 H 2(g) + O 2(g) 2 H 2 O(g) H rxn = - 483. 6 k. J/mol The difference in is due to the fact that heat has to be added to liquid water to convert it into a gas. In fact, at T = 25. 0 °C H 2 O(l) H 2 O(g) H rxn = + 44. 0 k. J/mol

We can check this as follows. If we add the first two reactions below we get the third reaction as our final result. 2 H 2(g) + O 2(g) 2 H 2 O(l) 2 H 2 O(g) H rxn = - 571. 6 k. J/mol H rxn = + 88. 0 k. J/mol _____________________________ 2 H 2(g) + O 2(g) 2 H 2 O(g) H rxn = - 483. 6 k. J/mol Since enthalpy is a state function (path independent) the change in enthalpy for the combination of the first two processes has to be the same as the change in enthalpy for the third process. This is a simple example of a general principle called Hess’ law.

Relationship Between Hrxn and Urxn By definition, H = U + p. V. For a process carried out at constant pressure H = U + (p. V) = U + p V If V > 0 then H > U V = 0 then H = U V < 0 then H < U For chemical reactions it is usually true that | U| >> |p V| and so Urxn Hrxn For precise work we can apply a correction to correctly convert between Urxn and Hrxn. (using H = U + p V).
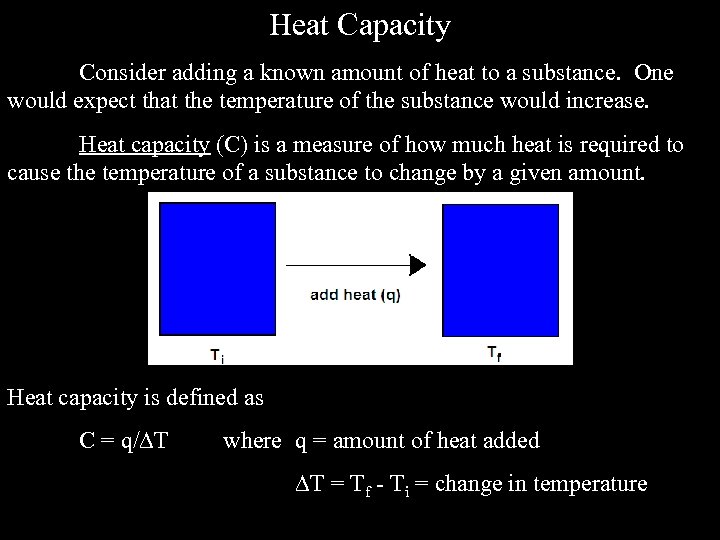
Heat Capacity Consider adding a known amount of heat to a substance. One would expect that the temperature of the substance would increase. Heat capacity (C) is a measure of how much heat is required to cause the temperature of a substance to change by a given amount. Heat capacity is defined as C = q/ T where q = amount of heat added T = Tf - Ti = change in temperature

Notes on Heat Capacity 1) Since C = q/ T, the units for C are (energy)/(temperature). The derived MKS units for C are J/K, though it is often given in J/ C. 2) Note that the numerical value for C when expressed in J/K or J/ C is identical. That is because we are using the change in temperature. Since the size of a degree Kelvin and a degree Celsius is the same, the numerical value for T is the same whether expressed in K or C. Example: Ti = 15. 0 C (288. 2 K) and Tf = 21. 5 C (294. 7 K) T = Tf – Ti = 21. 5 C – 15. 0 C = 6. 5 C = 294. 7 K - 288. 2 K = 6. 5 K 3) C is not in general a state function, since q is not a state function. However, if we restrict ourselves to processes occurring under conditions of constant pressure then C is a state function.

Specific Heat and Molar Heat Capacity There are two quantities that are closely related to heat capacity. Specific heat, (s) - The heat capacity per gram of substance. Molar heat capacity, (Cm) - The heat capacity per mole of substance. The relationships between C, s, and Cm (heat capacity, specific heat, and molar heat capacity) are as follows: s = C/m where m= mass of substance Cm = C/n where n = moles of substance So s has units of J/g C and Cm has units of J/mol C. Note that C is an extensive property, but s and Cm are intensive properties.

Heat Capacity Problem The initial temperature of a metal block of mass 38. 44 g is Ti = 18. 3 °C. After the addition of 132. J of heat the temperature of the metal increases to a final value Tf = 25. 7 °C. What are C and s for the metal block?

The initial temperature of a metal block of mass 38. 44 g is Ti = 18. 3 °C. After the addition of 132. J of heat the temperature of the metal increases to a final value Tf = 25. 7 °C. What are C and s for the metal block? From the definition of heat capacity C= heat absorbed = q = 132. J = 18. J/°C change in temperature T (25. 7 °C - 18. 3 °C) s= C= m 18. J/°C = 0. 46 J/g C 38. 44 g Note that C is an extensive property but s is an intensive property of the metal.

Specific Heat For Common Substances Substance s (J/g°C) Al(s) 0. 900 Au(s) 0. 129 C(graphite) 0. 720 C(diamond) 0. 502 Cu(s) 0. 385 Fe(s) 0. 444 Hg(l) 0. 139 H 2 O(l) 4. 184 Pb(s) 0. 128 Sn(s) 0. 227 Zn(s) 0. 389 The above table is at T = 25. C. Note that water has an unusually large value for heat capacity, which acts to moderate temperatures for cities surrounded by large bodies of water.

Calorimetry is the experimental method used to measure the heat produced or taken up in a chemical reaction or physical process. The device used in these measurements is called a calorimeter. If the heat capacity and temperature change for the calorimeter are known, we can find the value for q for the process If the process is carried out at constant pressure, then qsys = H If the process is carried out at constant volume, then qsys = U

Constant Pressure Calorimetry In a coffee cup calorimeter a chemical reaction or other process is carried out under conditions of constant pressure.

Example A metal block of mass 14. 486 g at an initial temperature of 74. 25 °C is placed inside a coffee cup calorimeter containing 100. 00 g of water at a temperature of 17. 42 °C. After equilibrium is reached the final temperature of the water is 20. 84 °C. What is s, the specific heat, of the metal? (Note: s = 4. 184 J/g°C for water. )

A metal block of mass 14. 486 g at an initial temperature of 74. 25 °C is placed inside a coffee cup calorimeter containing 100. 00 g of water at a temperature of 17. 42 °C. After equilibrium is reached the final temperature of the water is 20. 84 °C. What is s, the specific heat, of the metal? (Note: s = 4. 184 J/g°C for water. ) qwater = - qmetal swater mwater Twater = - smetal mmetal Tmetal smetal = - swater (mwater/mmetal)( Twater/ Tmetal ) So smetal = - (4. 184 J/g°C) 100. 00 g (20. 84 °C - 17. 42 °C) 14. 486 g (20. 84 °C - 74. 25 °C) = 1. 85 J/g°C Note we did not take into account the heat capacity of the calorimeter itself, but assumed it was small. For more precise work the heat capacity of the calorimeter would need to be included in the calculations.
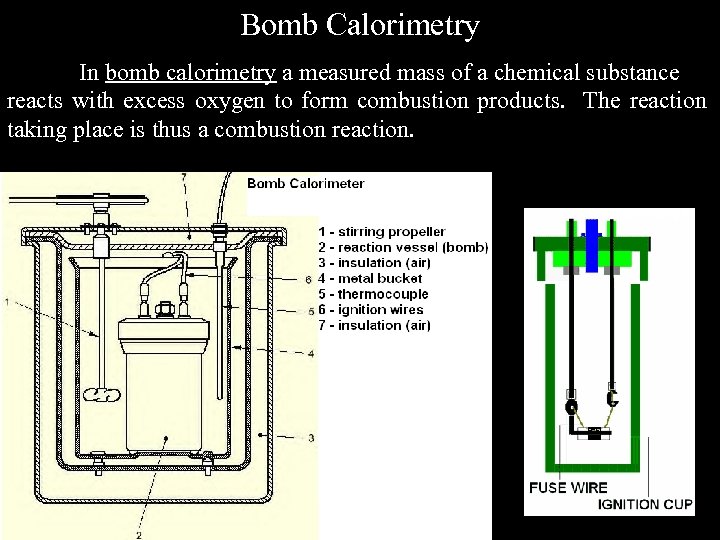
Bomb Calorimetry In bomb calorimetry a measured mass of a chemical substance reacts with excess oxygen to form combustion products. The reaction taking place is thus a combustion reaction.

Bomb Calorimetry Calculations If the heat capacity of the calorimeter apparatus is known (and this can be determined experimentally) then q = - C T C = heat capacity of calorimeter T = Tf - Ti = change in temperature The negative sign in the above equation occurs because we are measuring the value of q for the surroundings, and qsys = - qsur. If we know the energy of combustion for a compound, in units of k. J/g, then we can say q = m Ucom m = mass of compound burned Ucom = energy of combustion (in k. J/g) Note that by burning a known amount of a compound whose value for Ucom is known, and measuring T, we can find C, the heat capacity of the calorimeter.

Bomb Calorimetry Example: 1. 412 g of carbon (M = 12. 01 g/mol) are burned in a bomb calorimeter (C = 10325. J/ C). The temperature of the calorimeter increases by 4. 48 C. What are U (change in internal energy) and Um (change in internal energy per mole of carbon) for the process.

Example: 1. 412 g of carbon (M = 12. 01 g/mol) are burned in a bomb calorimeter (C = 10325. J/ C). The temperature of the calorimeter changes by 4. 48 C. What are U (change in internal energy) and Um (change in internal energy per mole of carbon) for the process. q = - C T = - (10325. J/ C) (4. 48 C) = - 46300. J For a process carried out at constant volume q = U, so U = - 46300. J Finally, the change in internal energy per mole of carbon is Um = U/n n = 1. 412 g 1 mol = 0. 1176 mol 12. 01 g Um = - 46300. J = - 393000 J/mol = - 393. k. J/mol 0. 1176 mol Note that Hm Um = - 393. k. J/mol, as previously noted.

Standard Conditions and Standard State It is convenient to report thermodynamic data for a particular set of conditions. These conditions are called thermodynamic standard conditions, and are usually (but not always) taken to be p = 1. 00 atm*, T = 25. 0 C = 298. 2 K. The standard state for an element is the most stable form of the element for standard conditions. carbon C(s) nitrogen N 2(g) bromine Br 2(l) oxygen O 2(g) iron Fe(s) argon Ar(g) mercury Hg (l) chlorine Cl 2(g) sulfur S(s) _____________________________ * Technically, standard pressure is now taken to be 1. 00 bar = 0. 987 atm. This makes only a minor difference in values for thermodynamic quantities.

Enthalpy of Formation ( H f) The formation reaction for a substance is defined as the reaction that produces one mole of a single product out of elements in their standard state. Because of the way we have defined the formation reaction, we may have to use fractional stoichiometric coefficients for some or all of the reactants. The enthalpy change for this reaction is defined as the enthalpy of formation for the substance. H 2(g) + 1/2 O 2(g) H 2 O(l) H f(H 2 O(l)) = - 285. 8 k. J/mol H 2(g) + 1/2 O 2(g) H 2 O(g) H f(H 2 O(g)) = - 241. 8 k. J/mol C(s) + O 2(g) CO 2(g) H f(CO 2(g)) = - 393. 5 k. J/mol Pb(s) + C(s) + 3/2 O 2(g) Pb. CO 3(s) H f(Pb. CO 3(s)) = - 699. 1 k. J/mol 3/ 2 O 2(g) O 3(g) H f(O 3(g)) = + 143. 0 k. J/mol Data formation enthalpies are given in Appendix 2 of Burdge (with separate tables for inorganic and organic substances).

Note that based on the above definition it follows that the enthalpy of formation of an element in its standard state is 0. 0 k. J/mol. We may see this as follows: The formation reaction for N 2(g), by definition (formation of one mole of a single product out of elements in their standard state), is N 2(g) But nothing happens in the above process, and so it follows that H rxn = H f(N 2(g) ) = 0. 0 k. J/mol This will be true for any element in its standard (thermodynamically most stable) state.

Example: Write the formation reaction for carbon tetrachloride (CCl 4(l)), acetone (CH 3 COCH 3(l)), and nitrous oxide (N 2 O(g)).

Example: Write the formation reaction for carbon tetrachloride (CCl 4(l)), acetone (CH 3 COCH 3(l)), and nitrous oxide (N 2 O(g)). C(s) + 2 Cl 2(g) CCl 4(l) 3 C(s) + 3 H 2(g) + ½ O 2(g) CH 3 COCH 3(l) N 2(g) + ½ O 2(g) N 2 O(g) Note that the enthalpy change when 1 mole of any of the above reactions is carried out corresponds to the enthalpy of formation for the substance.

Enthalpy of Combustion ( H com) The combustion reaction for a substance is defined as the reaction of one mole of a single substance with O 2(g) to form combustion products. Because of the way in which we have defined the combustion reaction we may have to use fractional coefficients for some of the reactants and products. The enthalpy change for this reaction is defined as the enthalpy of combustion for the substance. Combustion products for common elements are C CO 2(g) H H 2 O(l) N N 2(g) S SO 2(g) CH 4(g) + 2 O 2(g) CO 2(g) + 2 H 2 O(l) H com(CH 4(g)) = - 890. 3 k. J/mol C 6 H 6( ) + 15/2 O 2(g) 6 CO 2(g) + 3 H 2 O(l) H com(C 6 H 6( )) = - 3267. 4 k. J/mol

Writing Formation and Combustion Reactions We may use the definition of formation reaction and combustion reaction to write own the balanced chemical equations corresponding to these reactions. Example: Hexane (C 6 H 14(l)) is a hydrocarbon often used as a solvent in organic reactions. Write the formation reaction and the combustion reaction for hexane. CH 3 CH 2 CH 2 CH 3

Example: Hexane (C 6 H 14(l)) is a hydrocarbon often used as a solvent in organic reactions. Write the formation reaction and the combustion reaction for hexane. Formation - One mole of a single product out of elements in their standard state. ? C 6 H 14(l) 6 C(s) + 7 H 2(g) C 6 H 14(l) (balanced) Combustion - One mole of a single reactant, plus oxygen, to form combustion products. C 6 H 14(l) + ? O 2(g) ? C 6 H 14(l) + ? O 2(g) 6 CO 2(g) + 7 H 2 O(l) C 6 H 14(l) + 19/2 O 2(g) 6 CO 2(g) + 7 H 2 O(l) (balanced)

Enthalpy Change For Phase Transitions There are three phase transitions that can occur by adding heat to a substance. s l fusion (melting) H fus l g vaporization H vap s g sublimation H sub The enthalpy change when one mole of a substance undergoes the transition is defined as the enthalpy change for the phase transition. It represents the amount of heat required to convert one mole of the substance from the initial phase to the final phase. H 2 O(l) H 2 O(g) H vap(H 2 O) = 40. 7 k. J/mol at T = 100. 0 C Unlike other processes, the temperature for a phase transition is usually taken to be the temperature for which the two phases exist at equilibrium when p = 1. 0 atm, called the normal transition point.

Hess’ Law We previously noted that the change in the value for a state function depends only on initial and final state and is independent of the path used to travel between the two states. We may put this in a more formal manner in terms of Hess’ law – The change in value for any state function will be the same for any process or combination of processes that have the same initial and final state. We are particularly interested in applying Hess’ law to chemical reactions.

Hess’ Law For a Chemical Reaction Let us use Hess’ law to find the value for ( H rxn) for the following chemical reaction: Ca. CO 3(s) Ca. O(s) + CO 2(g) H rxn

Hess’ Law For a Chemical Reaction Let us use Hess’ law to find the value for ( H rxn) for the following chemical reaction: Ca. CO 3(s) Ca. O(s) + CO 2(g) H rxn We may obtain this same reaction as follows: Ca(s) + ½ O 2(g) Ca. O(s) H f(Ca. O(s)) C(s) + O 2(g) CO 2(g) H f(CO 2(g)) Ca. CO 3(s) Ca(s) + C(s) + 3/2 O 2(g) - H f(Ca. CO 3(s)) Ca. CO 3(s) Ca. O(s) + CO 2(g) H rxn So by Hess’ law, H rxn = [ H f(Ca. O(s)) + H f(CO 2(g)) ] - [ H f(Ca. CO 3(s)) ] We can get H rxn using only data on enthalpies of formation!

General Method For Finding H rxn Based on the same procedure used in the previous example the following general relationship can be derived H rxn = [ H f(products) ] - [ H f(reactants) ] Notice what this means. If we have a table formation enthalpies we can find the value for H rxn for any chemical reaction. In fact, the same general procedure can be used to find the values for the change in any state function. Also note that when we use the superscript this indicates not only standard conditions but also standard concentrations for reactants and products. gases p = 1. 0 atm solutes [M] = 1. 0 mol/L solids, liquids, solvents must be present in the system

Example: Find H rxn for the conversion of acetylene into dichloroethane C 2 H 2(g) + 2 HCl(g) CH 2 Cl(l)

Example: Find H rxn for the conversion of acetylene into dichloroethane C 2 H 2(g) + 2 HCl(g) CH 2 Cl(l) H rxn = [ H f(CH 2 Cl(l)) ] - [ H f(C 2 H 2(g)) + 2 H f(HCl(g))] = [ (- 165. 2 k. J/mol) ] - [ (226. 7 k. J/mol) + 2 ( - 92. 3 k. J/mol) ] = - 207. 3 k. J/mol Thermodynamic data are given in the Appendix 2 of Burdge, with separate tables for inorganic and organic substances.

Other Uses of Hess’ Law Hess’ law can be used to find H rxn for any process that can be written as a combination of other chemical reactions whose values for H rxn are known. Example: Consider the formation reaction 5 C(s) + 6 H 2(g) C 5 H 12(l) H rxn = ? Using the following information find H rxn for this reaction (1) C 5 H 12(l) + 8 O 2(g) 5 CO 2(g) + 6 H 2 O(g) H rxn = - 3505. 8 k. J/mol (2) C(s) + O 2(g) CO 2(g) H rxn = - 393. 5 k. J/mol (3) 2 H 2(g) + O 2(g) 2 H 2 O(g) H rxn = - 483. 5 k. J/mol Note all of the above are combustion reactions, which are particularly easy to carry out experimentally.

Example: Consider the formation reaction 5 C(s) + 6 H 2(g) C 5 H 12(l) H rxn = ? Using the following information find H rxn for this reaction (1) C 5 H 12(l) + 8 O 2(g) 5 CO 2(g) + 6 H 2 O(g) H rxn = - 3505. 8 k. J/mol (2) C(s) + O 2(g) CO 2(g) H rxn = - 393. 5 k. J/mol (3) 2 H 2(g) + O 2(g) 2 H 2 O(g) H rxn = - 483. 5 k. J/mol reverse 1 st reaction 5 CO 2(g) + 6 H 2 O(g) C 5 H 12(l) + 8 O 2(g) H rxn = + 3505. 8 k. J/mol 5 times the 2 nd reaction 5 C(s) + 5 O 2(g) 5 CO 2(g) H rxn = - 1967. 5 k. J/mol 3 times 3 rd reaction 6 H 2(g) + 3 O 2(g) 6 H 2 O(g) 5 C(s) + 6 H 2(g) C 5 H 12(l) H rxn = - 1450. 5 k. J/mol H rxn = + 87. 8 k. J/mol

End of Chapter 5 “In this house we obey the laws of thermodynamics!” - Homer Simpson “. . . the Dutch physicist Heike Kamerlingh Onnes gave H the name enthalpy, from the Greek (in) and (heat), or from the single Greek word (enthalpos), to warm within. ” K. J. Laidler, The World of Physical Chemistry “[Thermodynamics] is the only physical theory of universal content which, within the framework of the applicability of its basic concepts, I am convinced will never be overthrown. ” Albert Einstein
4ede83aa6f8bdbcc6007522b35a2fdf6.ppt