Скачать презентацию Homework 1 is due now Today T-test and Скачать презентацию Homework 1 is due now Today T-test and

aa6e86c51eeeeb8ab3a273e8451bff99.ppt

  • Количество слайдов: 32

Homework #1 is due now Today: T-test and Outliers xkcd. com Homework #1 is due now Today: T-test and Outliers xkcd. com

• Stats practice in next lab • Also need to start putting together • Stats practice in next lab • Also need to start putting together your group for inquiry 2. . . 3 -5 people/group • Inquiry 1 written and oral reports are due in lab Th 9/24 or M 9/28 • Homework #2 is posted. . . Stream Open House • Homework #3 will ask you to complete some online safety training • Online evaluation • More TA office hours

How significant of a difference is this? Set 1= 2, 2, 2, 3, 3, How significant of a difference is this? Set 1= 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 7 Mean = 3. 67 ± 1. 6 range = 2. 07 to 5. 27 And Set 2= 8, 6, 7, 8, 9, 5, 6, 7, 9, 8, 9, 5 Mean = 7. 25 ± 1. 48 range = 5. 77 to 8. 73 No overlap, might be different

The ‘Students’ T-test is a method to assign a numerical value of statistical difference. The ‘Students’ T-test is a method to assign a numerical value of statistical difference.

The ‘Students’ T-test is a method to assign a numerical value of statistical difference. The ‘Students’ T-test is a method to assign a numerical value of statistical difference.

The ‘Students’ T-test is a method to assign a numerical value of statistical difference. The ‘Students’ T-test is a method to assign a numerical value of statistical difference. (Difference between means) (variance) (sample size)

The ‘Students’ T-test is a method to assign a numerical value of statistical difference. The ‘Students’ T-test is a method to assign a numerical value of statistical difference. T is then used to look up the P-value from a table. Also need ‘degrees of freedom’ = (n 1+n 2)-1.

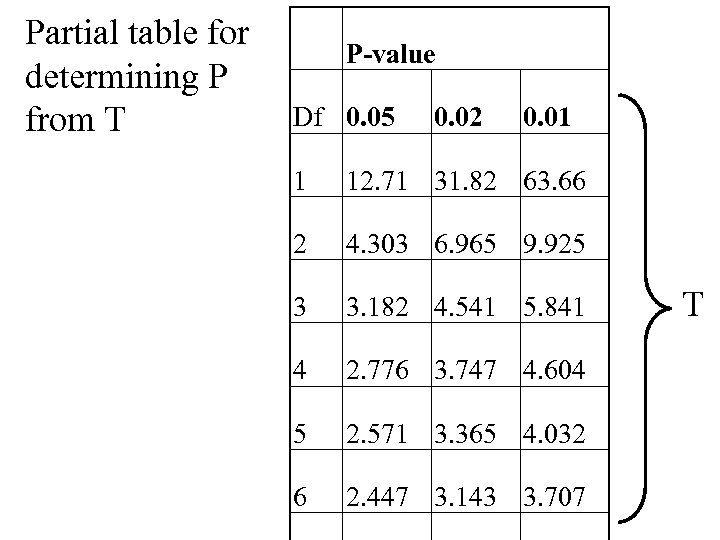Partial table for determining P from T P-value Df 0. 05 0. 02 0. Partial table for determining P from T P-value Df 0. 05 0. 02 0. 01 1 12. 71 31. 82 63. 66 2 4. 303 6. 965 9. 925 3 3. 182 4. 541 5. 841 4 2. 776 3. 747 4. 604 5 2. 571 3. 365 4. 032 6 2. 447 3. 143 3. 707 T

How significant of a difference is this? Using a speadsheet to get a P How significant of a difference is this? Using a speadsheet to get a P value = 3. 44 x 10 -6. Set 1= 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 7 Mean = 3. 67 ± 1. 6 And Set 2= 8, 6, 7, 8, 9, 5, 6, 7, 9, 8, 9, 5 Mean = 7. 25 ± 1. 48

How significant of a difference is this? P value = 3. 44 x 10 How significant of a difference is this? P value = 3. 44 x 10 -6. So the chance that these 2 sets of data are not significantly different is 3. 44 x 10 -6 Set 1= 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 7 Mean = 3. 67 ± 1. 6 And Set 2= 8, 6, 7, 8, 9, 5, 6, 7, 9, 8, 9, 5 Mean = 7. 25 ± 1. 48

How significant of a difference is this? P value = 3. 44 x 10 How significant of a difference is this? P value = 3. 44 x 10 -6. So the chance that these 2 sets of data are significantly different is 1 - 3. 44 x 10 -6 or 0. 999996559 We can be 99. 9996559% certain that the difference is statistically significant. Set 1= 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 7 Mean = 3. 67 ± 1. 6 Set 2= 8, 6, 7, 8, 9, 5, 6, 7, 9, 8, 9, 5 Mean = 7. 25 ± 1. 48

Overlap, different means, but might not be a statistically significant difference Set 1= 2, Overlap, different means, but might not be a statistically significant difference Set 1= 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 7 Mean = 3. 67 ± 1. 6 range = 2. 07 to 5. 27 Set 2= 8, 6, 7, 8, 9, 5, 6, 7, 9, 8, 4, 5 Mean = 6. 83 ± 1. 64 range = 5. 19 to 8. 47 P-value = 4. 41 x 10 -5

What is, or is not, a statistically significant difference? 20% random difference : 80% What is, or is not, a statistically significant difference? 20% random difference : 80% confidence 10% random difference : 90% confidence 5% random difference : 95% confidence 1% random difference : 99% confidence 0. 1% random difference : 99. 9% confidence

Generally a P-value of 0. 05 or less is considered a statistically significant difference. Generally a P-value of 0. 05 or less is considered a statistically significant difference. 20% random difference : 80% confidence 10% random difference : 90% confidence 5% random difference : 95% confidence 1% random difference : 99% confidence 0. 1% random difference : 99. 9% confidence

Standard deviation is NOT a valid method for determining statistical signifigance. T-test is one Standard deviation is NOT a valid method for determining statistical signifigance. T-test is one valid and accurate method for determining if 2 means have a statistically significant difference, or if the difference is merely by chance.

Outliers… 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 7, Outliers… 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 7, 121, 130 Median = 4 Mean = 18

Outliers: When is data invalid? Outliers: When is data invalid?

Outliers: When is data invalid? Not simply when you want it to be. Outliers: When is data invalid? Not simply when you want it to be.

Outliers: When is data invalid? Not simply when you want it to be. Dixon’s Outliers: When is data invalid? Not simply when you want it to be. Dixon’s Q test can determine if a value is statistically an outlier.

Dixon’s Q test can determine if a value is statistically an outlier. Dixon’s Q test can determine if a value is statistically an outlier.

Dixon’s Q test can determine if a value is statistically an outlier. Example: results Dixon’s Q test can determine if a value is statistically an outlier. Example: results from a blood test… 789, 700, 772, 766, 777

Dixon’s Q test can determine if a value is statistically an outlier. Example: results Dixon’s Q test can determine if a value is statistically an outlier. Example: results from a blood test… 789, 700, 772, 766, 777

Dixon’s Q test can determine if a value is statistically an outlier. Example: results Dixon’s Q test can determine if a value is statistically an outlier. Example: results from a blood test… 789, 700, 772, 766, 777 Q=|(700 – 766)| ÷ |(789 – 700)|

Dixon’s Q test can determine if a value is statistically an outlier. Example: results Dixon’s Q test can determine if a value is statistically an outlier. Example: results from a blood test… 789, 700, 772, 766, 777 Q =|(700 – 766)| ÷ |(789 – 700)| = 0. 742

Dixon’s Q test can determine if a value is statistically an outlier. Example: results Dixon’s Q test can determine if a value is statistically an outlier. Example: results from a blood test… 789, 700, 772, 766, 777 Q =|(700 – 766)| ÷ |(789 – 700)| = 0. 742 So?

You need the critical values for Q table: Sample # Q critical value 3 You need the critical values for Q table: Sample # Q critical value 3 0. 970 4 0. 831 5 0. 717 6 0. 621 7 0. 568 10 0. 466 12 0. 426 15 0. 384 20 0. 342 25 0. 317 If Q calc > Q crit rejected From: E. P. King, J. Am. Statist. Assoc. 48: 531 (1958)

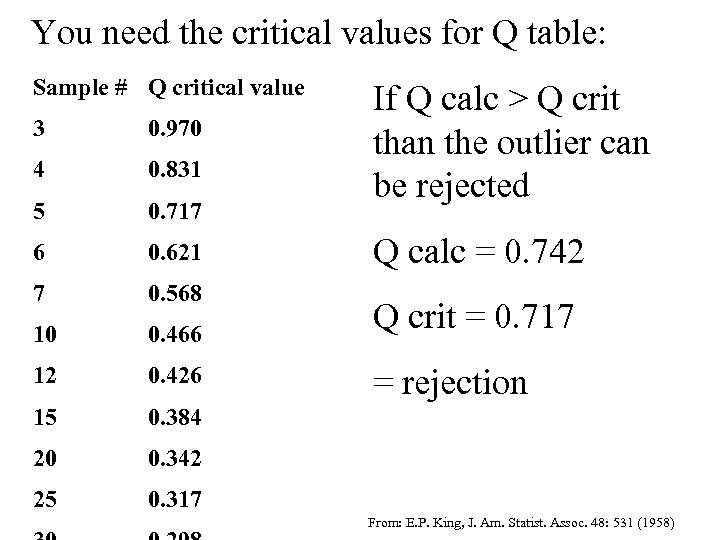You need the critical values for Q table: Sample # Q critical value 3 You need the critical values for Q table: Sample # Q critical value 3 0. 970 4 0. 831 5 0. 717 6 0. 621 7 0. 568 10 0. 466 12 0. 426 15 0. 384 20 0. 342 25 If Q calc > Q crit than the outlier can be rejected 0. 317 Q calc = 0. 742 Q crit = 0. 717 = rejection From: E. P. King, J. Am. Statist. Assoc. 48: 531 (1958)

What can outliers tell us? What can outliers tell us?

If you made a mistake, you should have already accounted for that. If you made a mistake, you should have already accounted for that.

Outliers can lead to important and fascinating discoveries. Transposons “jumping genes” were discovered because Outliers can lead to important and fascinating discoveries. Transposons “jumping genes” were discovered because they did not fit known modes of inheritance.

Homework #1 is due now and homework #2 is posted Next: R 2, Samples, Homework #1 is due now and homework #2 is posted Next: R 2, Samples, and Populations xkcd. com