36730cc888ab6819c705c07a825dcee5.ppt
- Количество слайдов: 34


Higher Tier - Number revision Contents : Calculator questions Long multiplication & division Best buy questions Estimation Units Speed, Distance and Time Density, Mass and Volume Percentages Products of primes HCF and LCM Indices Standard Form Ratio Fractions with the four rules Upper and lower bounds Percentage error Surds Rational and irrational numbers Recurring decimals as fractions Direct proportion Inverse proportion Graphical solutions to equations

Calculator questions Which buttons would you press to do these on a calculator ? 2. 5 + 4. 1 3. 5 1. 7 + 2. 8 2. 3 – 0. 2 1. 56 8. 5 x 103 3. 4 x 10 -1 4 1000 1. 72 + 5. 22 6. 31 9. 2 6. 1 – 7. 5 8 3 2. 5 1 1 – 3. 6 2. 3
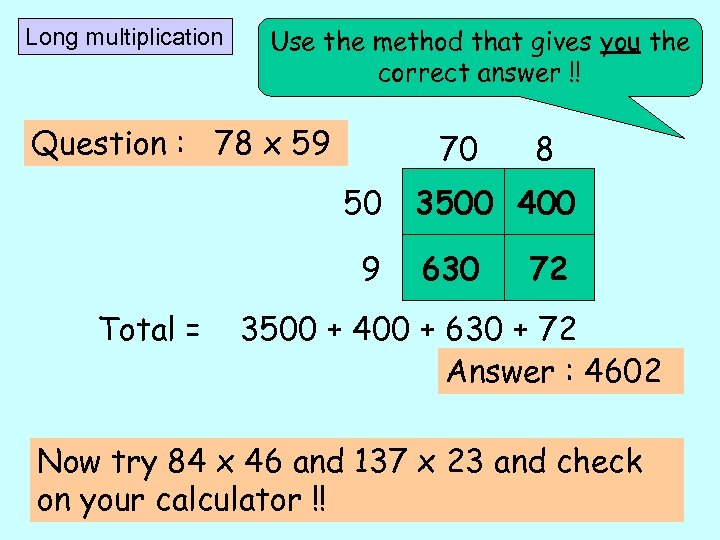
Long multiplication Use the method that gives you the correct answer !! Question : 78 x 59 70 50 9 Total = 8 3500 400 630 72 3500 + 400 + 630 + 72 Answer : 4602 Now try 84 x 46 and 137 x 23 and check on your calculator !!
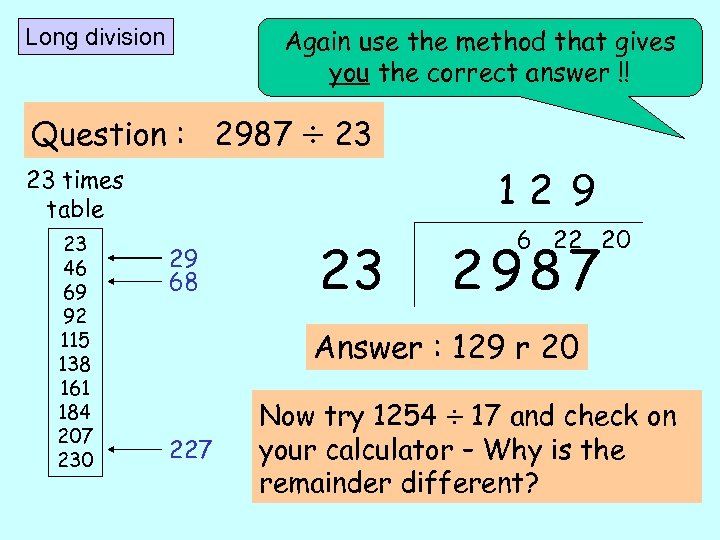
Again use the method that gives you the correct answer !! Long division Question : 2987 23 12 9 23 times table 23 46 69 92 115 138 161 184 207 230 29 68 23 6 22 20 2987 Answer : 129 r 20 227 Now try 1254 17 and check on your calculator – Why is the remainder different?

Best buy questions Always divide by the price to see how much 1 pence will buy you Beans Large 400 87 = 4. 598 g/p Small 150 34 = 4. 412 g/p Large is better value (more grams for every penny spent) 32 p 0. 95 L 78 p OR 2. 1 L 87 p 34 p OR Milk Large 2. 1 78 = 0. 0269 L/p Small 0. 95 32 = 0. 0297 L/p Small is better value OR (looking at it differently) {Large 78 2. 1 = 37. 14 p/L Small 32 0. 95 = 33. 68 p/L}
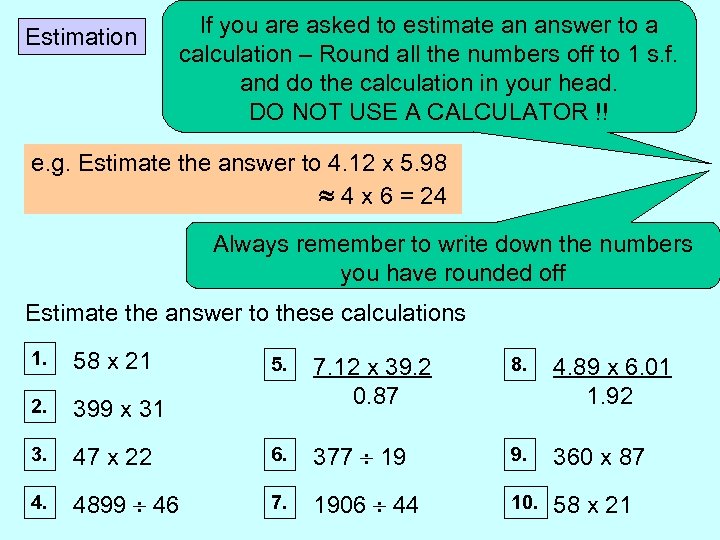
Estimation If you are asked to estimate an answer to a calculation – Round all the numbers off to 1 s. f. and do the calculation in your head. DO NOT USE A CALCULATOR !! e. g. Estimate the answer to 4. 12 x 5. 98 4 x 6 = 24 Always remember to write down the numbers you have rounded off Estimate the answer to these calculations 1. 58 x 21 2. 399 x 31 3. 4. 5. 7. 12 x 39. 2 0. 87 8. 4. 89 x 6. 01 1. 92 47 x 22 6. 377 19 9. 360 x 87 4899 46 7. 1906 44 10. 58 x 21
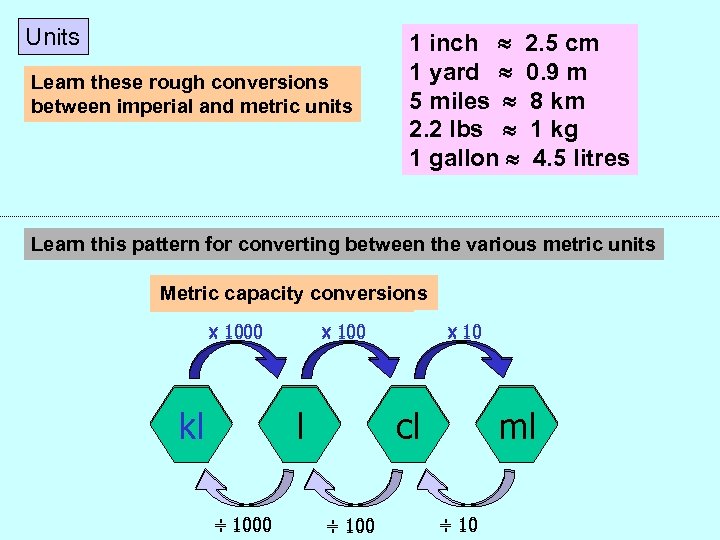
Units Learn these rough conversions between imperial and metric units 1 inch 2. 5 cm 1 yard 0. 9 m 5 miles 8 km 2. 2 lbs 1 kg 1 gallon 4. 5 litres Learn this pattern for converting between the various metric units Metriccapacityconversions weight conversions Metric length conversions x 1000 km kg kl ÷ 1000 x 100 m g l x 10 cm cg cl ÷ 100 mm mg ml ÷ 10

Speed, Distance, Time questions Speed, Distance and Time are linked by this formula S = To complete questions check that all units are compatible, substitute your values in and rearrange if necessary. 1. Speed = 45 m/s Time = 2 minutes Distance = ? 45 m/s and 120 secs S= D T 45 = D. 120 45 x 120 = D D = 5400 m 2. Distance = 17 miles Time = 25 minutes Speed = ? 17 miles and 0. 417 hours S= D T S= 17. 0. 417 S = 40. 8 mph 3. D T Speed = 65 km/h Distance = 600 km Time = ? S= D T 65 = 600. T T = 600. 65 T = 9. 23 hours

Density, Mass, Volume questions Density, Mass and Volume are linked by this formula M D = V To complete questions check that all units are compatible, substitute your values in and rearrange if necessary. 1. Density = 8 g/cm 3 Volume = 6 litres Mass = ? 8 g/cm 3 and 6000 cm 3 D= M V 8= M. 6000 8 x 6000 = M M = 48000 g ( or M = 48 kg) 2. Mass = 5 tonnes Volume = 800 m 3 Density = ? 800 m 3 and 5000 kg D= M V D = 5000. 800 D = 6. 25 kg/m 3 3. Density = 12 kg/m 3 Mass = 564 kg Volume = ? D= M V 12 = 564. V V = 564. 12 V = 47 m 3
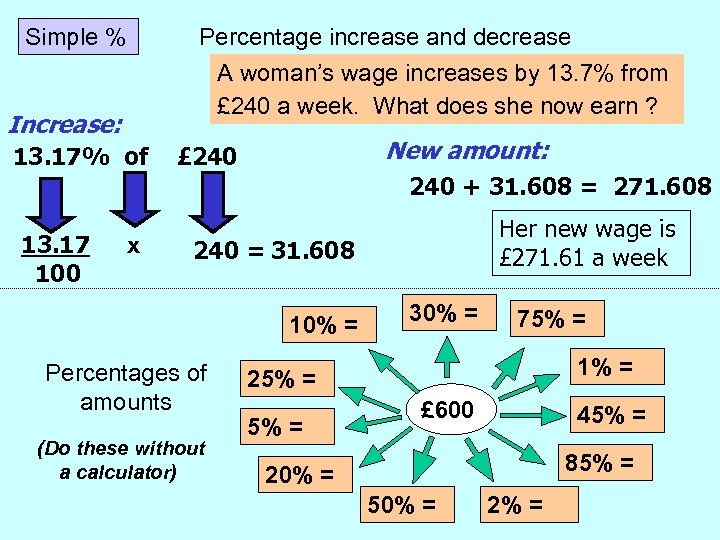
Simple % Percentage increase and decrease A woman’s wage increases by 13. 7% from £ 240 a week. What does she now earn ? Increase: 13. 17% of New amount: £ 240 + 31. 608 = 271. 608 13. 17 100 x Her new wage is £ 271. 61 a week 240 = 31. 608 10% = Percentages of amounts (Do these without a calculator) 30% = 75% = 1% = 25% = £ 600 45% = 85% = 20% = 50% = 2% =
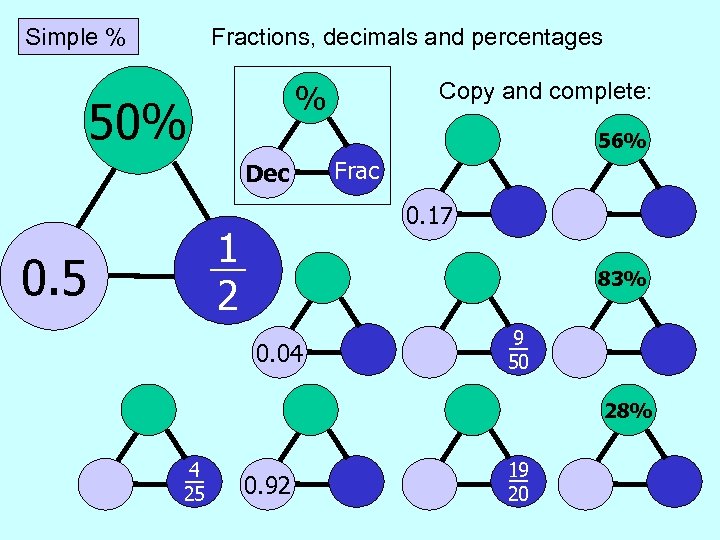
Simple % Fractions, decimals and percentages 50% 56% Dec Frac 0. 17 1 2 0. 5 Copy and complete: % 83% 0. 04 9 50 28% 4 25 0. 92 19 20
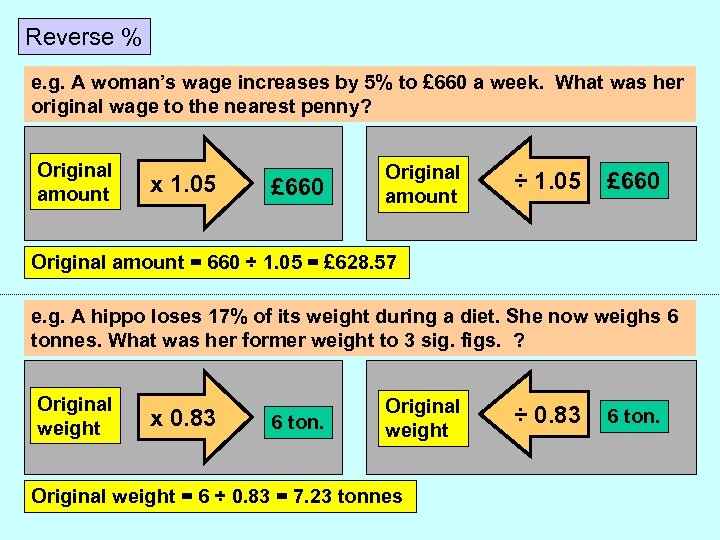
Reverse % e. g. A woman’s wage increases by 5% to £ 660 a week. What was her original wage to the nearest penny? Original amount x 1. 05 £ 660 Original amount ÷ 1. 05 £ 660 Original amount = 660 ÷ 1. 05 = £ 628. 57 e. g. A hippo loses 17% of its weight during a diet. She now weighs 6 tonnes. What was her former weight to 3 sig. figs. ? Original weight x 0. 83 6 ton. Original weight = 6 ÷ 0. 83 = 7. 23 tonnes ÷ 0. 83 6 ton.

Repeated % e. g. A building society gives 6. 5% interest p. a. on all money invested there. If John pays in £ 12000, how much will he have in his account This at the end of 5 years. is not the correct method: £ 12000 x 0. 065 = 780 x 1. 065 x 5 = 3900 x 1. 065 12000 + 3900 = £ 15900 x 1. 065 ? He will have = 12000 x (1. 065)5 = £ 16441. 04 e. g. A car loses value at a rate of approximately 23% each year. Estimate how much a $40000 car be worth in four years ? This is not the correct method: 40000 x 0. 23 = 9200 x 0. 77 £ 40000 x 0. 77 ? 9200 x 4 = 36800 40000 – 36800 = $3200 The car’s new value = 40000 x (0. 77)4 = $14061 (nearest $)
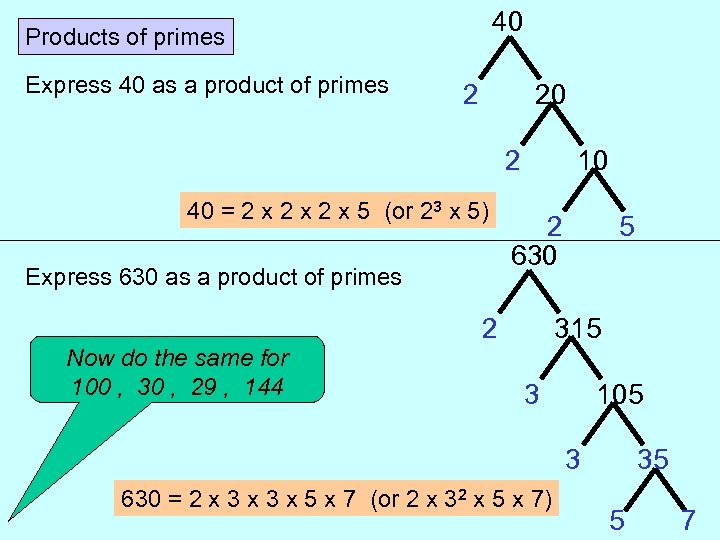
40 Products of primes Express 40 as a product of primes 2 20 2 40 = 2 x 2 x 5 (or 23 x 5) Express 630 as a product of primes 10 2 630 2 Now do the same for 100 , 30 , 29 , 144 5 315 3 105 3 630 = 2 x 3 x 5 x 7 (or 2 x 32 x 5 x 7) 35 5 7

HCF Expressing 2 numbers as a product of primes can help you calculate their Highest common factor HCF e. g. Find the highest common factor of 84 and 120. 30. Consider the numbers 20 and Their Pick out all the bits that factors are: 84 = 2 x 3 x 7 1, 2, 4, 5, 10, 20 and 1, 2, 3, 5, 6, 10, 15, 30 are common to both. 120 = 2 x 2 x 3 highest common factor is 10 Their x 5 Highest common factor = 2 x 3 = 12 LCM Expressing 2 numbers as a product of primes can also help you calculate their Lowest common multiple LCM e. g. Find the lowest common multiple of 300 and 504. Consider the numbers 16 and 20. Their multiplesout the highest Pick are: 300 = 22 x 3 x 52 valued 40, 60, each 16, 32, 48, 64, 80, 96 and 20, index for 80, 100 504 = 23 x 32 x 7 lowest common multiple is 80 prime factor. Their Lowest common multiple = 23 x 32 x 52 x 7 = 12600
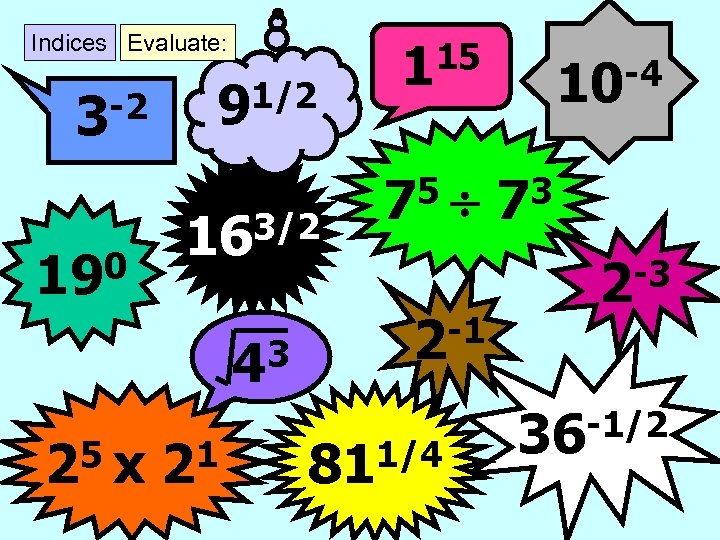
Indices Evaluate: -2 3 0 19 1/2 9 3/2 16 3 4 5 x 2 15 1 5 7 -1 2 1/4 81 -4 10 3 7 -3 2 -1/2 36

Standard form Write in Standard Form 9. 6 0. 0001 3 600 0. 041 56 x 103 0. 2 8 900 000 Write as an ordinary number 4. 7 x 109 1 x 102 8 x 10 -3 5. 1 x 104 7 x 10 -2 8. 6 x 10 -1 9. 2 x 103 3. 5 x 10 -3 Calculate 3 x 104 x 7 x 10 -1 without a calculator Calculate 4. 6 x 104 ÷ 2. 5 x 108 with a calculator Calculate 1. 5 x 106 ÷ 3 x 10 -2 without a calculator
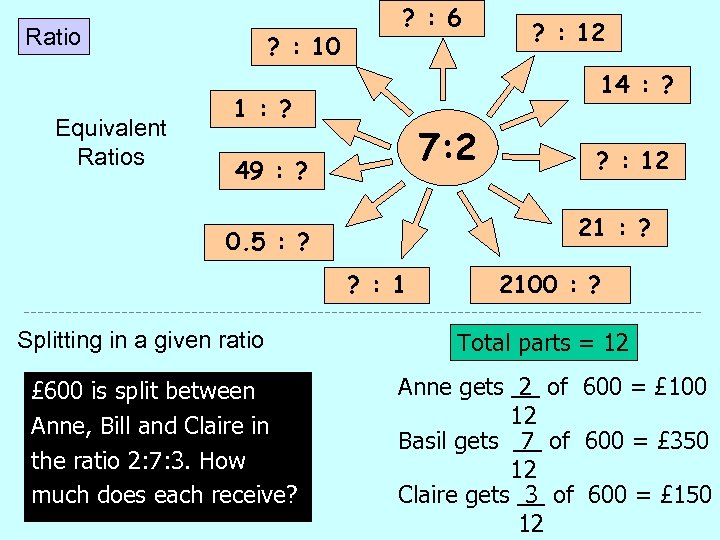
Ratio Equivalent Ratios ? : 10 ? : 6 14 : ? 1 : ? 7: 2 49 : ? ? : 1 £ 600 is split between Anne, Bill and Claire in the ratio 2: 7: 3. How much does each receive? ? : 12 21 : ? 0. 5 : ? Splitting in a given ratio ? : 12 2100 : ? Total parts = 12 Anne gets 2 of 600 = £ 100 12 Basil gets 7 of 600 = £ 350 12 Claire gets 3 of 600 = £ 150 12

Fractions with the four rules +–×÷ Learn these steps to complete all fractions questions: • Always convert mixed fractions into top heavy fractions before you start • When adding or subtracting the “bottoms” need to be made the same • When multiplying two fractions, multiply the “tops” together and the “bottoms” together to get your final fraction • When dividing one fraction by another, turn the second fraction on its head and then treat it as a multiplication

Fractions with the four rules 4⅔ 1½ 4⅔ + 1½ = = 14 3 28 6 37 6 6 + + 3 2 9 6 = = = 1 6 = 14 3 28 9 3 1 9 3 2 2 3

Upper and lower bounds A journey of 37 km measured to the nearest km could actually be as long as 37. 49999999…. km or as short as 36. 5 km. It could not be 37. 5 as this would round up to 38 but the lower and upper bounds for this measurement are 36. 5 and 37. 5 defined by: 36. 5 < Actual distance < 37. 5 e. g. Write down the Upper and lower bounds of each of these values given to the accuracy stated: 9 m (1 s. f. ) 85 g (2 s. f. ) 8. 5 to 9. 5 84. 5 to 85. 5 180 weeks (2 s. f. ) 175 to 185 2. 40 m (2 d. p. ) 2. 395 to 2. 405 4000 L (2 s. f. ) 3950 to 4050 60 g (nearest g) 59. 5 to 60. 5 e. g. A sector of a circle of radius 7 cm makes an angle of 32 0 at the centre. Find its minimum possible area if all measurements are given to the nearest unit. ( = 3. 14) 320 7 cm Area = ( /360) x x r Minimum area = (31. 5/360) x 3. 14 x 6. 5 Minimum area = 11. 61 cm 2
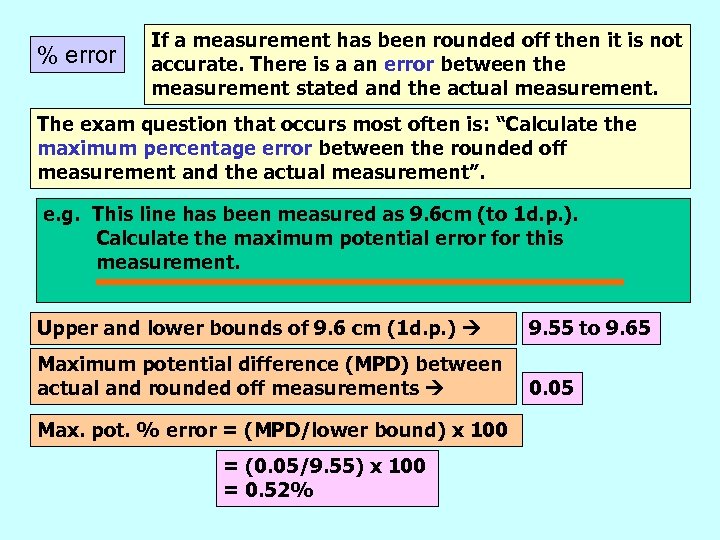
% error If a measurement has been rounded off then it is not accurate. There is a an error between the measurement stated and the actual measurement. The exam question that occurs most often is: “Calculate the maximum percentage error between the rounded off measurement and the actual measurement”. e. g. This line has been measured as 9. 6 cm (to 1 d. p. ). Calculate the maximum potential error for this measurement. Upper and lower bounds of 9. 6 cm (1 d. p. ) 9. 55 to 9. 65 Maximum potential difference (MPD) between actual and rounded off measurements 0. 05 Max. pot. % error = (MPD/lower bound) x 100 = (0. 05/9. 55) x 100 = 0. 52%
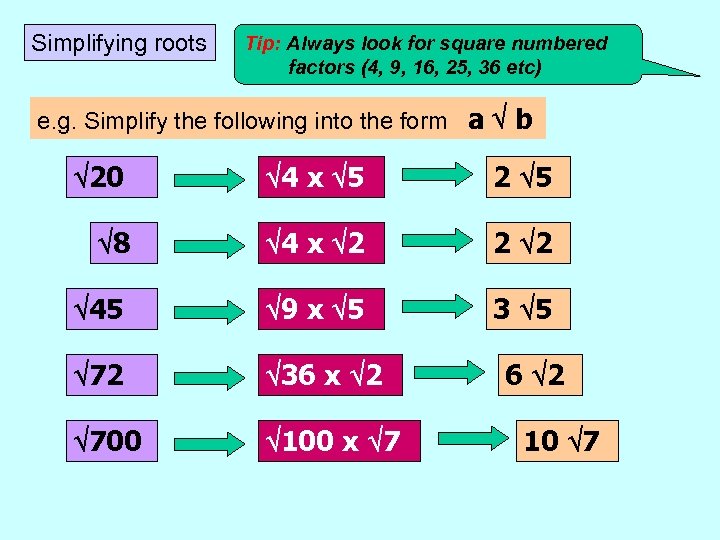
Simplifying roots Tip: Always look for square numbered factors (4, 9, 16, 25, 36 etc) e. g. Simplify the following into the form a b 20 4 x 5 2 5 8 4 x 2 2 2 45 9 x 5 3 5 72 36 x 2 700 100 x 7 6 2 10 7

Surds A surd is the name given to a number which has been left in the form of a root. So 5 has been left in surd form. SIMPLIFYING EXPRESSIONS WITH SURDS IN A surd or a combination of surds can be simplified using the rules: M x N = MN and visa versa M ÷ N = M/N and visa versa 12 4 x 3 135 ÷ 3 5( 5 + 20) ( 3 – 1)2 Tips: Deal with a surd as you would an algebraic term and always look for square numbers 2 3 45 9 x 5 5 + 100 ( 3 – 1) LEAVING ANSWERS IN SURD FORM Pythagoras ( 14)2 = ( 6)2 + x 2 14 = 6 + x 2 x = 8 Answer: x = 2 2 3 5 15 3 – 3 + 1 4 – 2 3 Calculate the length of side x in surd form (non-calculator paper): 14 x 6

Rational and irrational numbers Rational numbers can be expressed in the form a/b. Terminating decimals (3. 17 or 0. 022) and recurring decimals (0. 3333. . or 4. 7676. . ) are rational. Irrational numbers cannot be made into fractions. Non-terminating and non-recurring decimals (3. 4526473… or 2) are irrational. State whether the following are rational or irrational numbers: 16 52 3 1/5 20 2. 3/5. 7 What do you need to do to make the following irrational numbers into rational numbers: 3 53 3 6 20 2 2. 7

Recurring decimals as fractions Learn this technique which changes recurring decimals into fractions: Express 0. 7777…. . as a fraction. Let n = 0. 7777…. . so 10 n = 7. 7777…. . so 9 n = 7 so n = 7/9 Express 2. 3434…. . as a fraction. Let n= 2. 3434…. . so 100 n = 234. 3434…. . so 99 n = 232 so n = 232/99 Express 0. 413213213…. . as a fraction. Let n= 0. 4132132132…. . so 10000 n = 4132. 132132132…. . and 10 n = 4. 132132132…… so 9990 n = 4128 so n = 4128/9990 n = 688/1665
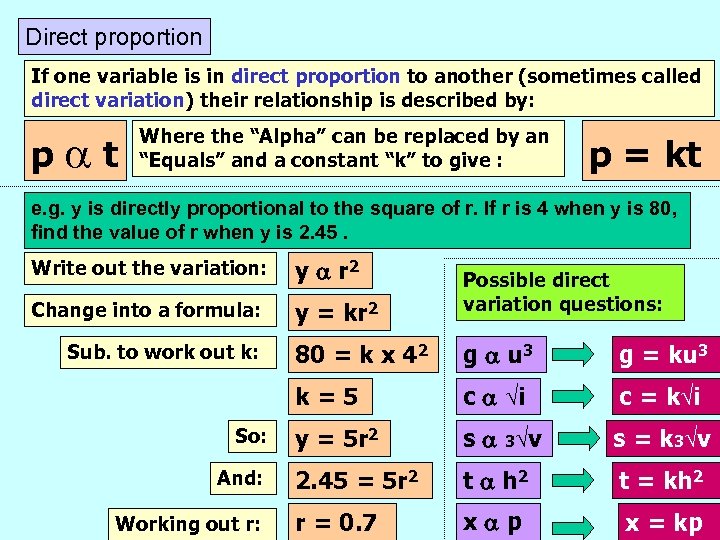
Direct proportion If one variable is in direct proportion to another (sometimes called direct variation) their relationship is described by: p t Where the “Alpha” can be replaced by an “Equals” and a constant “k” to give : p = kt e. g. y is directly proportional to the square of r. If r is 4 when y is 80, find the value of r when y is 2. 45. Write out the variation: y r 2 Change into a formula: y = kr 2 Possible direct variation questions: So: And: Working out r: 80 = k x 42 g u 3 g = ku 3 k=5 Sub. to work out k: c i c = k i y = 5 r 2 s 3 v s = k 3 v 2. 45 = 5 r 2 t h 2 t = kh 2 r = 0. 7 x p x = kp

Inverse proportion If one variable is inversely proportion to another (sometimes called inverse variation) their relationship is described by: p 1/t Again “Alpha” can be replaced by a constant “k” to give : p = k/t e. g. y is inversely proportional to the square root of r. If r is 9 when y is 10, find the value of r when y is 7. 5. Write out the variation: y 1/ r Change into a formula: y = k/ r Possible inverse variation questions: So: 10 = k/ 9 g 1/u 3 g = k/u 3 k = 30 Sub. to work out k: c 1/ i c = k/ i y = 30/ r s 1/3 v s = k/3 v And: 7. 5 = 30/ r t 1/h 2 t = k/h 2 Working out r: r = 16 (not 2) x 1/p x = k/p
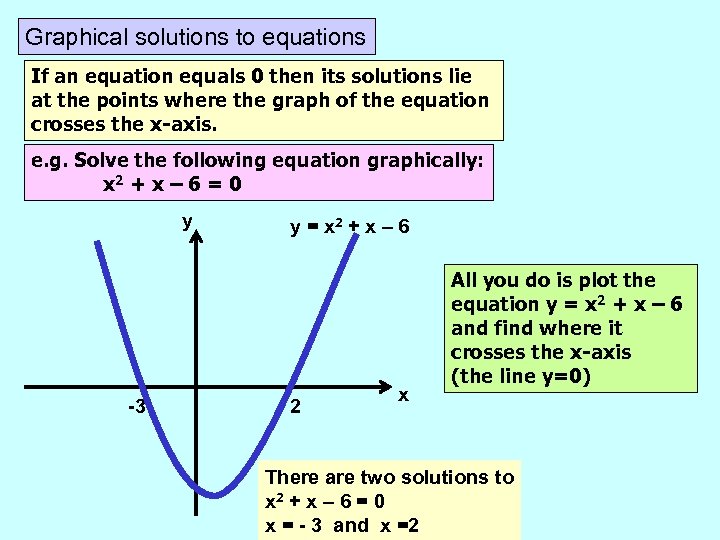
Graphical solutions to equations If an equation equals 0 then its solutions lie at the points where the graph of the equation crosses the x-axis. e. g. Solve the following equation graphically: x 2 + x – 6 = 0 y -3 y = x 2 + x – 6 2 x All you do is plot the equation y = x 2 + x – 6 and find where it crosses the x-axis (the line y=0) There are two solutions to x 2 + x – 6 = 0 x = - 3 and x =2
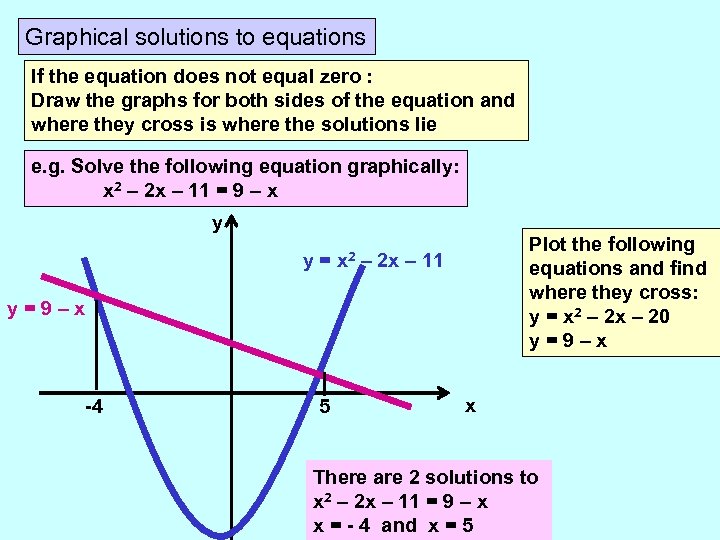
Graphical solutions to equations If the equation does not equal zero : Draw the graphs for both sides of the equation and where they cross is where the solutions lie e. g. Solve the following equation graphically: x 2 – 2 x – 11 = 9 – x y y= x 2 Plot the following equations and find where they cross: y = x 2 – 2 x – 20 y=9–x – 2 x – 11 y=9–x -4 5 x There are 2 solutions to x 2 – 2 x – 11 = 9 – x x = - 4 and x = 5
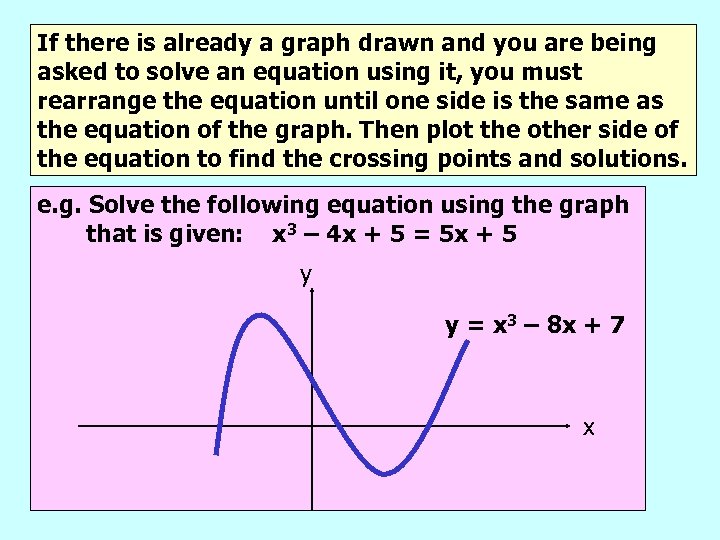
If there is already a graph drawn and you are being asked to solve an equation using it, you must rearrange the equation until one side is the same as the equation of the graph. Then plot the other side of the equation to find the crossing points and solutions. e. g. Solve the following equation using the graph that is given: x 3 – 4 x + 5 = 5 x + 5 y y = x 3 – 8 x + 7 x
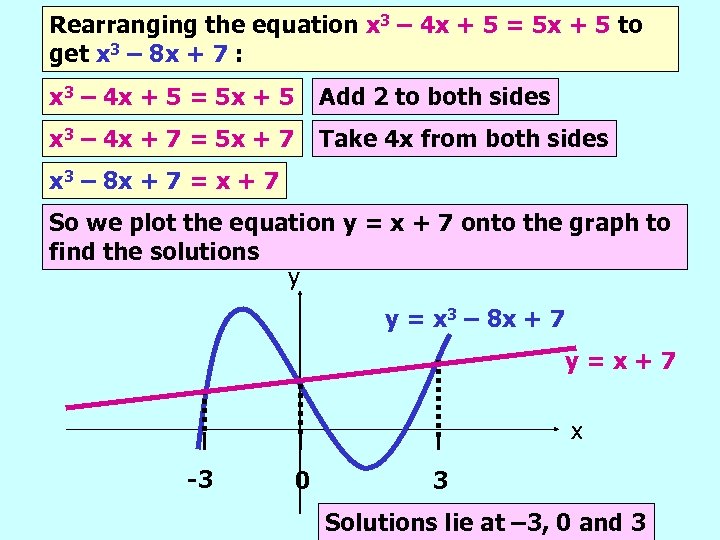
Rearranging the equation x 3 – 4 x + 5 = 5 x + 5 to get x 3 – 8 x + 7 : x 3 – 4 x + 5 = 5 x + 5 Add 2 to both sides x 3 – 4 x + 7 = 5 x + 7 Take 4 x from both sides x 3 – 8 x + 7 = x + 7 So we plot the equation y = x + 7 onto the graph to find the solutions y y = x 3 – 8 x + 7 y=x+7 x -3 0 3 Solutions lie at – 3, 0 and 3

State the graphs you need to plot to solve the following equations describing how you will find your solutions: 1. 2. 3. 4. 5. 6. 3 x 2 + 4 x – 2 = 0 7 x + 4 = x 2 – 4 x x 4 + 5 = 0 0 = 8 x 2 – 5 x 2 x = 9 6 x 3 = 2 x 2 + 5 1. 2. 3. 4. 4 x 2 + 4 x – 6 = 0 4 x 2 + x - 2 = 7 4 x 2 – 3 x = 2 x 3 x 2 = – 5 If you have got the graph of y= 4 x 2 + 5 x – 6 work out the other graph you need to draw to solve each of the following equations: Solve this equation graphically: x 3 + 8 x 2 + 3 x = 2 x 2 – 2 x
36730cc888ab6819c705c07a825dcee5.ppt