Higher Tier Handling Data revision Contents

Higher Tier – Handling Data revision Contents : Questionnaires Sampling Scatter diagrams Pie charts Frequency polygons Histograms Averages Moving averages Mean from frequency table Estimating the mean Cumulative frequency curves Box and whisker plots Theoretical probability Experimental probability Probability tree diagrams

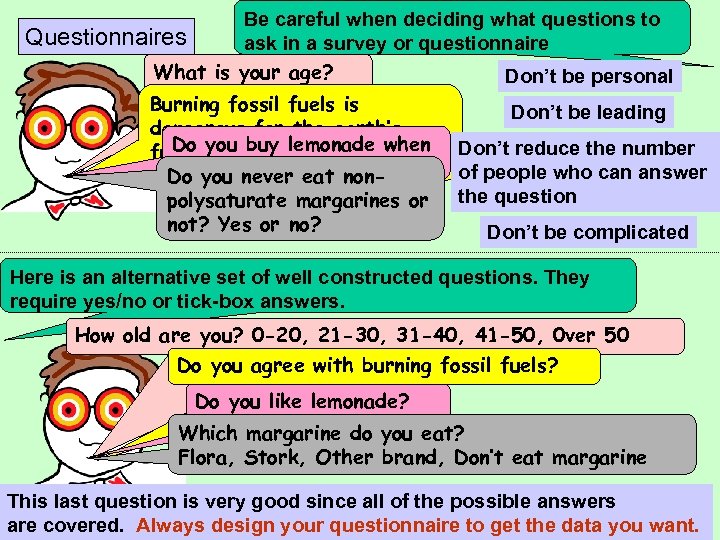Be careful when deciding what questions to Questionnaires ask in a survey or questionnaire What is your age? Don’t be personal Burning fossil fuels is dangerous for the earth’s Do you buy lemonade when future, don’t you agree? you are at Tescos? Do you never eat nonpolysaturate margarines or not? Yes or no? Don’t be leading Don’t reduce the number of people who can answer the question Don’t be complicated Here is an alternative set of well constructed questions. They require yes/no or tick-box answers. How old are you? 0 -20, 21 -30, 31 -40, 41 -50, 0 ver 50 Do you agree with burning fossil fuels? Do you like lemonade? Which margarine do you eat? Flora, Stork, Other brand, Don’t eat margarine This last question is very good since all of the possible answers are covered. Always design your questionnaire to get the data you want.

Sampling When it is impossible to ask a whole population to take part in a survey or a questionnaire, you have to sample a smaller part of the population. The larger Therefore the sample has to be representative of the sample the better population and not be biased. RANDOM SAMPLING Here every member of a population has an equal chance of being chosen: Names out of a bag, random numbers on a calculator, etc. STRATIFIED SAMPLING Here the population is firstly divided into categories and the number of people in each category is found out. The sample is then made up of these categories in the same proportions as they are in the population using % or a scaling down factor. The required numbers in each category are then selected randomly. Lets say the sample is 80 so we divide each The whole population = 215 amount by Age Male Female 215/80 0 -29 13 10 0 -29 34 26 =2. 6875 30 -59 17 20 30 -59 46 54 60 - 19 36 60 - 7 13

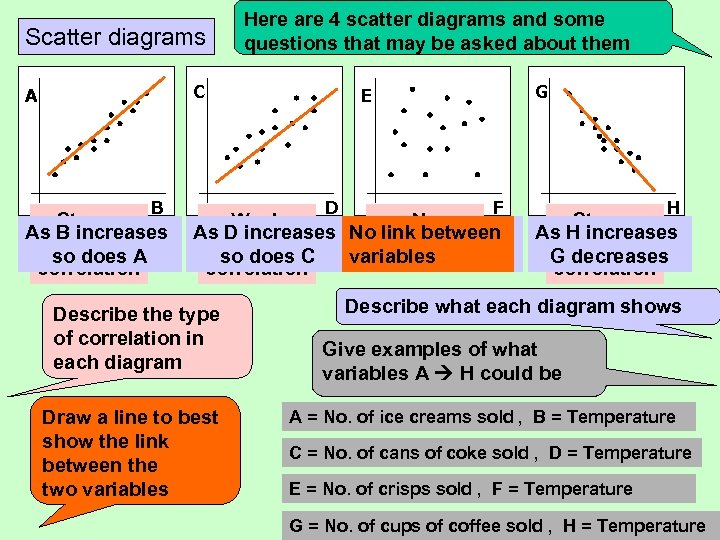Scatter diagrams Here are 4 scatter diagrams and some questions that may be asked about them C A B Strong As B increases positive so does A correlation G E D F Weak No As D increases No link between No relationship positive correlation so does C variables E and F between correlation Describe the type of correlation in each diagram Draw a line to best show the link between the two variables H Strong As H increases negative G decreases correlation Describe what each diagram shows Give examples of what variables A H could be A = No. of ice creams sold , B = Temperature C = No. of cans of coke sold , D = Temperature E = No. of crisps sold , F = Temperature G = No. of cups of coffee sold , H = Temperature

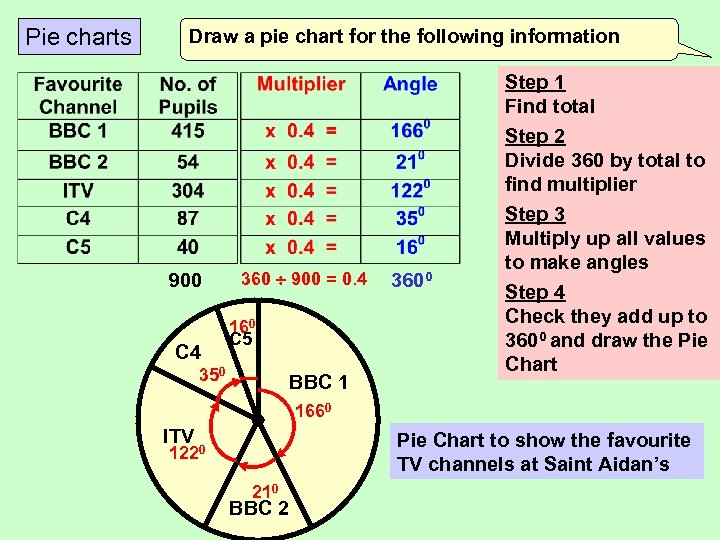Pie charts Draw a pie chart for the following information Step 1 Find total Step 2 Divide 360 by total to find multiplier 900 C 4 360 900 = 0. 4 160 C 5 350 BBC 1 3600 Step 3 Multiply up all values to make angles Step 4 Check they add up to 3600 and draw the Pie Chart 1660 ITV Pie Chart to show the favourite TV channels at Saint Aidan’s 1220 210 BBC 2

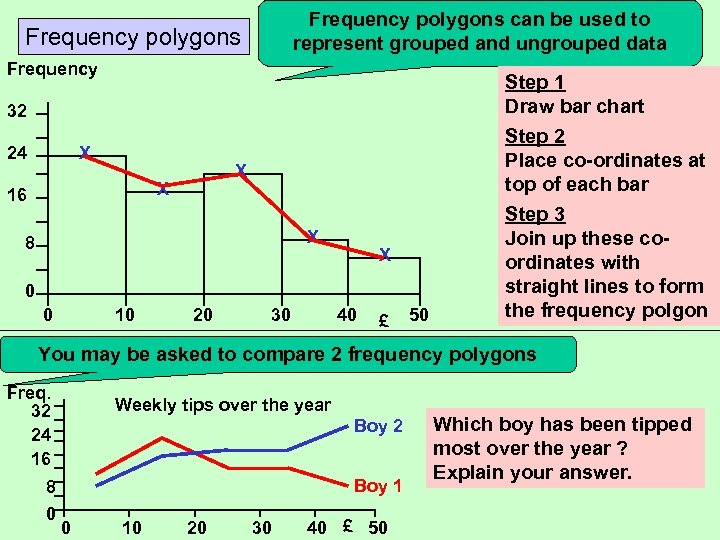Frequency polygons can be used to represent grouped and ungrouped data Frequency polygons Frequency Step 1 Draw bar chart Step 2 Place co-ordinates at top of each bar 32 24 X X X 16 X 8 X 0 0 10 20 30 40 £ 50 Step 3 Join up these coordinates with straight lines to form the frequency polgon You may be asked to compare 2 frequency polygons Freq. 32 24 16 Weekly tips over the year Boy 2 Boy 1 8 0 0 10 20 30 40 £ 50 Which boy has been tipped most over the year ? Explain your answer.

Histograms A histogram looks similar to a bar chart but there are 4 differences: • No gaps between the bars and bars can be different widths. • x-axis has continuous data (time, weight, length etc. ). • The area of each bar represents the frequency. • The y-axis is always labelled “Frequency density” where Frequency density = Frequency/width of class interval Example 1 : Draw a histogram for this data Length (cm) 0

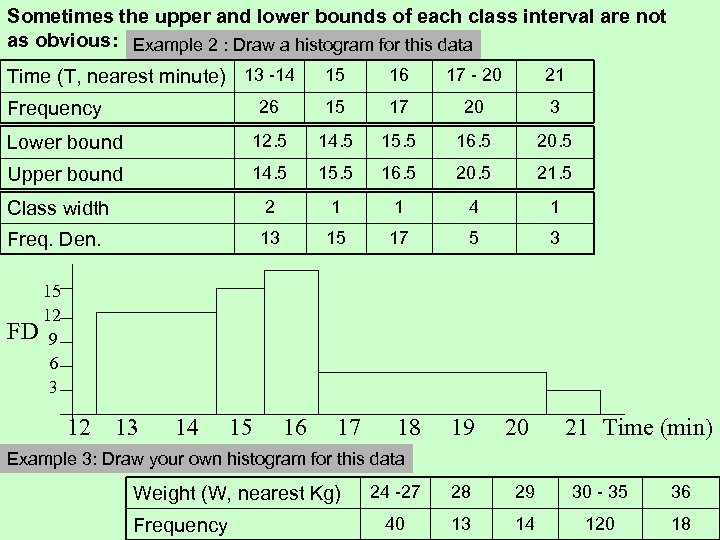Sometimes the upper and lower bounds of each class interval are not as obvious: Example 2 : Draw a histogram for this data Time (T, nearest minute) 13 -14 15 16 17 - 20 21 26 15 17 20 3 Lower bound 12. 5 14. 5 15. 5 16. 5 20. 5 Upper bound 14. 5 15. 5 16. 5 20. 5 21. 5 Class width 2 1 1 4 1 Freq. Den. 13 15 17 5 3 Frequency 15 12 FD 9 6 3 12 13 14 15 16 17 18 19 20 21 Time (min) Example 3: Draw your own histogram for this data Weight (W, nearest Kg) Frequency 24 -27 28 29 30 - 35 36 40 13 14 120 18

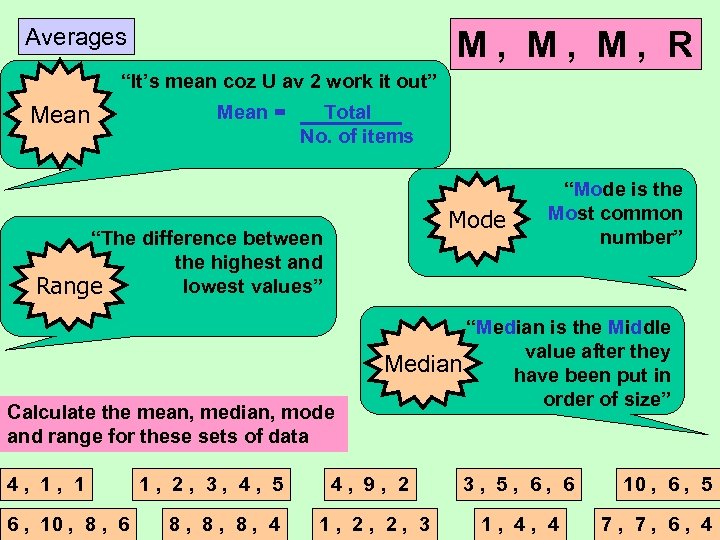Averages M, M, M, R “It’s mean coz U av 2 work it out” Mean = Total No. of items Mode “The difference between the highest and lowest values” Range Calculate the mean, median, mode and range for these sets of data 4, 1, 1 6 , 10 , 8 , 6 1, 2, 3, 4, 5 8, 8, 8, 4 “Mode is the Most common number” “Median is the Middle value after they Median have been put in order of size” 4, 9, 2 3, 5, 6, 6 1, 2, 2, 3 1, 4, 4 10 , 6 , 5 7, 7, 6, 4

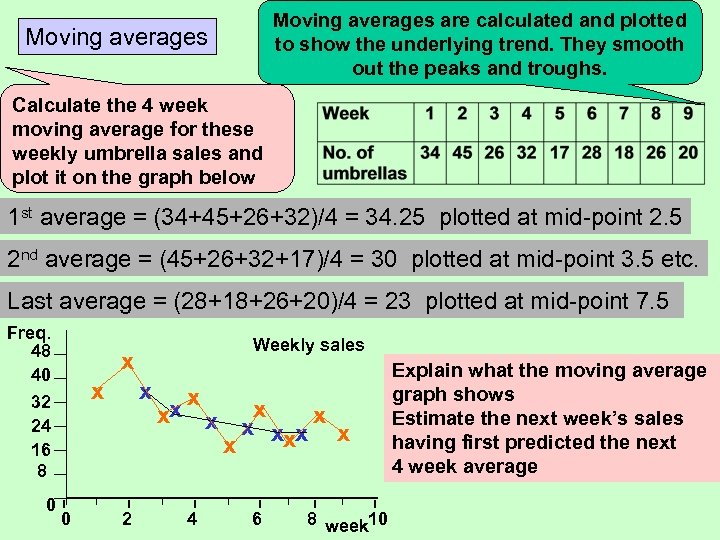Moving averages are calculated and plotted to show the underlying trend. They smooth out the peaks and troughs. Moving averages Calculate the 4 week moving average for these weekly umbrella sales and plot it on the graph below 1 st average = (34+45+26+32)/4 = 34. 25 plotted at mid-point 2. 5 2 nd average = (45+26+32+17)/4 = 30 plotted at mid-point 3. 5 etc. Last average = (28+18+26+20)/4 = 23 plotted at mid-point 7. 5 Freq. 48 40 32 24 16 8 0 Weekly sales x x 0 x 2 x x x xxx x 4 6 8 week 10 Explain what the moving average graph shows Estimate the next week’s sales having first predicted the next 4 week average

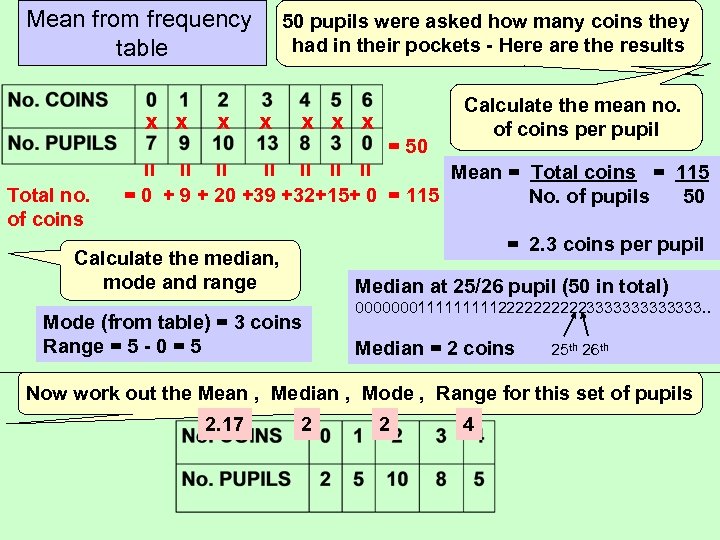Mean from frequency table x x x 50 pupils were asked how many coins they had in their pockets - Here are the results x x = 50 = = Mean = Total coins = 115 = 0 + 9 + 20 +39 +32+15+ 0 = 115 No. of pupils 50 = = = Total no. of coins Calculate the mean no. of coins per pupil = 2. 3 coins per pupil Calculate the median, mode and range Median at 25/26 pupil (50 in total) Mode (from table) = 3 coins Range = 5 - 0 = 5 000000011111222223333333. . Median = 2 coins 25 th 26 th Now work out the Mean , Median , Mode , Range for this set of pupils 2. 17 2 2 4

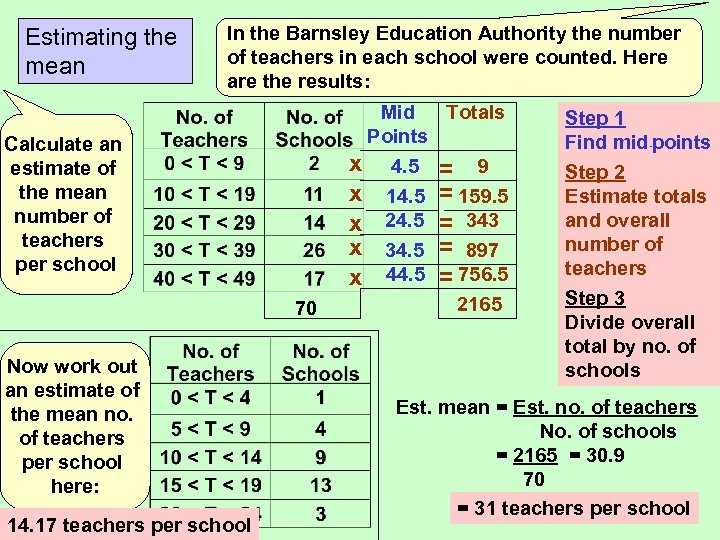Estimating the mean In the Barnsley Education Authority the number of teachers in each school were counted. Here are the results: Mid Totals Points Calculate an estimate of the mean number of teachers per school x x x 70 Now work out an estimate of the mean no. of teachers per school here: 14. 17 teachers per school 4. 5 14. 5 24. 5 34. 5 44. 5 = 9 = 159. 5 = 343 = 897 = 756. 5 2165 Step 1 Find mid-points Step 2 Estimate totals and overall number of teachers Step 3 Divide overall total by no. of schools Est. mean = Est. no. of teachers No. of schools = 2165 = 30. 9 70 = 31 teachers per school

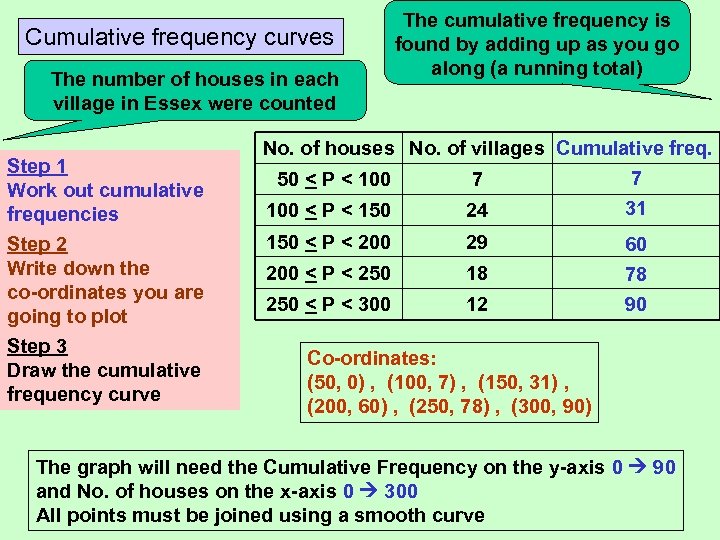Cumulative frequency curves The number of houses in each village in Essex were counted Step 1 Work out cumulative frequencies Step 2 Write down the co-ordinates you are going to plot Step 3 Draw the cumulative frequency curve The cumulative frequency is found by adding up as you go along (a running total) No. of houses No. of villages Cumulative freq. 7 50 < P < 100 7 31 100 < P < 150 24 150 < P < 200 29 200 < P < 250 18 250 < P < 300 12 60 78 90 Co-ordinates: (50, 0) , (100, 7) , (150, 31) , (200, 60) , (250, 78) , (300, 90) The graph will need the Cumulative Frequency on the y-axis 0 90 and No. of houses on the x-axis 0 300 All points must be joined using a smooth curve

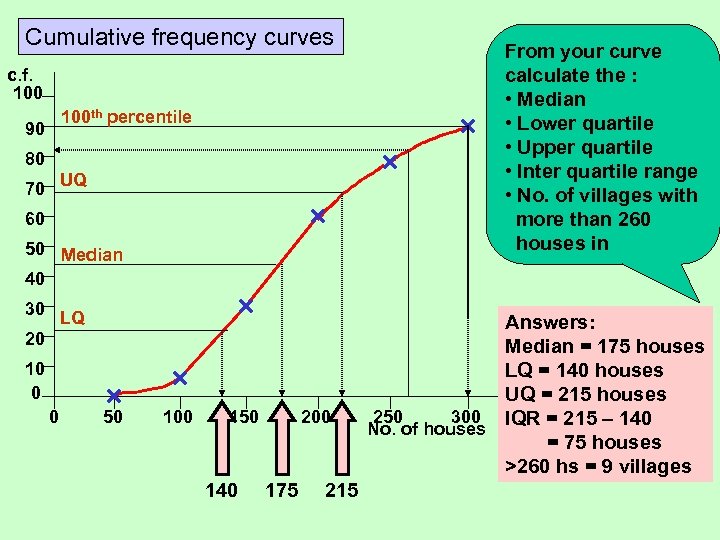Cumulative frequency curves c. f. 100 th percentile 90 80 UQ 70 60 50 Median 40 30 LQ 20 10 0 0 50 100 150 140 200 175 215 From your curve calculate the : • Median • Lower quartile • Upper quartile • Inter quartile range • No. of villages with more than 260 houses in Answers: Median = 175 houses LQ = 140 houses UQ = 215 houses 250 300 IQR = 215 – 140 No. of houses = 75 houses >260 hs = 9 villages

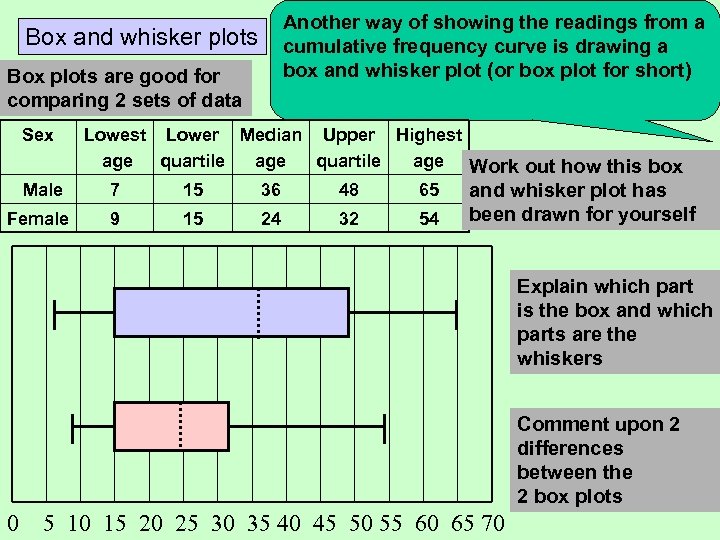Another way of showing the readings from a cumulative frequency curve is drawing a box and whisker plot (or box plot for short) Box and whisker plots Box plots are good for comparing 2 sets of data Sex Male Female Lowest Lower Median Upper Highest age quartile age Work out how this box 7 15 36 48 65 and whisker plot has 9 15 24 32 54 been drawn for yourself Explain which part is the box and which parts are the whiskers Comment upon 2 differences between the 2 box plots 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70

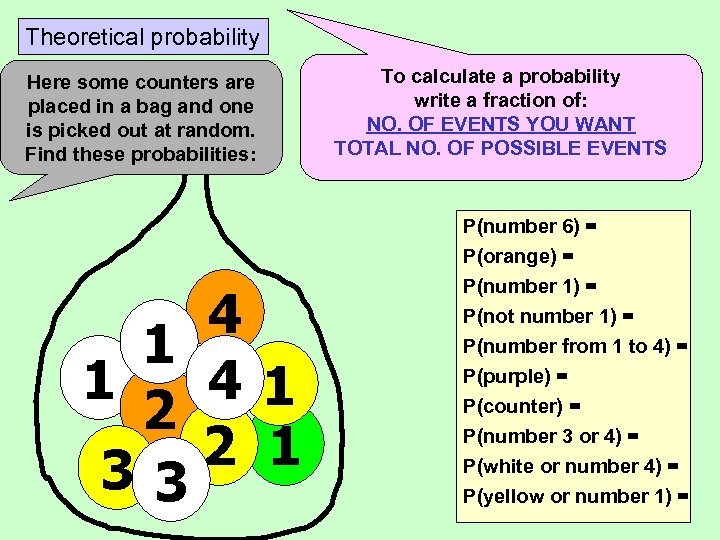Theoretical probability Here some counters are placed in a bag and one is picked out at random. Find these probabilities: 4 1 1 41 2 2 1 33 To calculate a probability write a fraction of: NO. OF EVENTS YOU WANT TOTAL NO. OF POSSIBLE EVENTS P(number 6) = P(orange) = P(number 1) = P(not number 1) = P(number from 1 to 4) = P(purple) = P(counter) = P(number 3 or 4) = P(white or number 4) = P(yellow or number 1) =

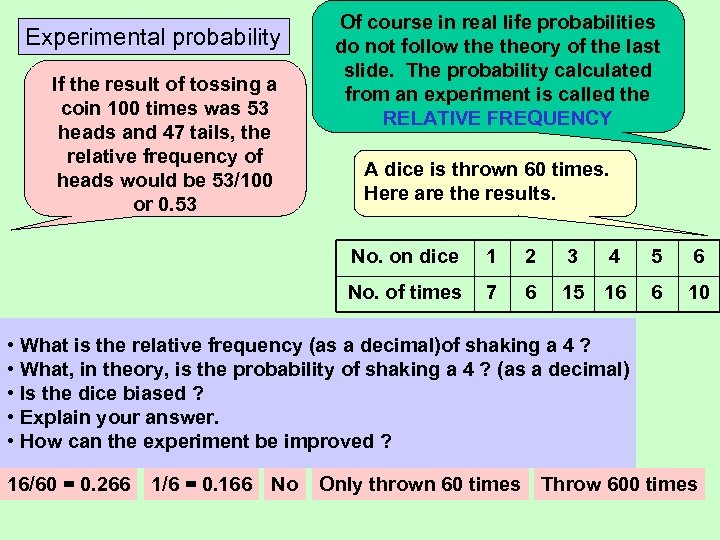Experimental probability If the result of tossing a coin 100 times was 53 heads and 47 tails, the relative frequency of heads would be 53/100 or 0. 53 Of course in real life probabilities do not follow theory of the last slide. The probability calculated from an experiment is called the RELATIVE FREQUENCY A dice is thrown 60 times. Here are the results. No. on dice 1 2 3 4 5 6 No. of times 7 6 15 16 6 10 • What is the relative frequency (as a decimal)of shaking a 4 ? • What, in theory, is the probability of shaking a 4 ? (as a decimal) • Is the dice biased ? • Explain your answer. • How can the experiment be improved ? 16/60 = 0. 266 1/6 = 0. 166 No Only thrown 60 times Throw 600 times

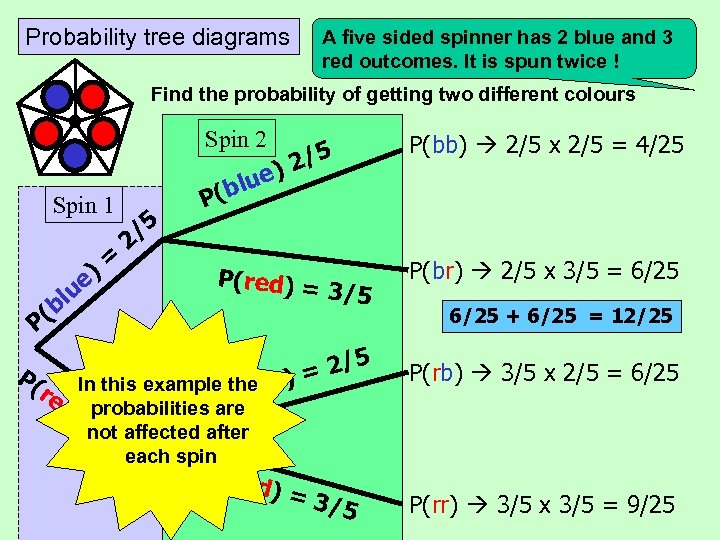Probability tree diagrams A five sided spinner has 2 blue and 3 red outcomes. It is spun twice ! Find the probability of getting two different colours Spin 2 Spin 1 )= e P( P( u bl /5 2 P lue (b 2/5 ) P(red) = the re In this example (blue) d) probabilities. P are = affected after not 3/ each spin 5 P(re 3/5 2/5 = d) = 3/5 P(bb) 2/5 x 2/5 = 4/25 P(br) 2/5 x 3/5 = 6/25 + 6/25 = 12/25 P(rb) 3/5 x 2/5 = 6/25 P(rr) 3/5 x 3/5 = 9/25

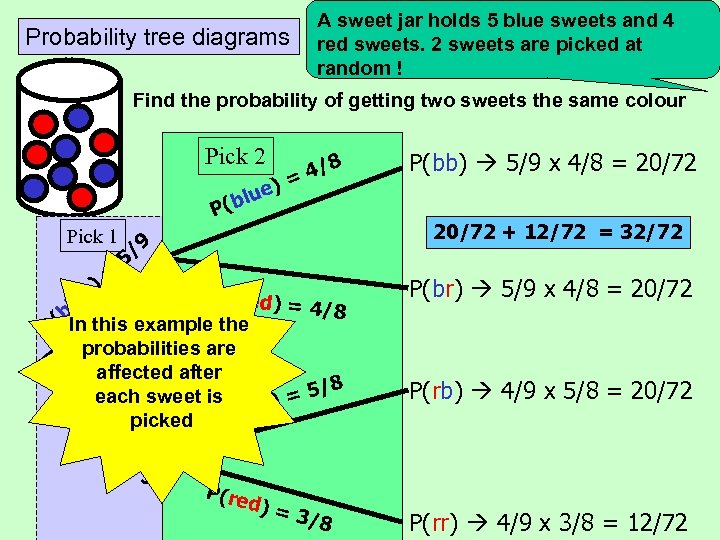Probability tree diagrams A sweet jar holds 5 blue sweets and 4 red sweets. 2 sweets are picked at random ! Find the probability of getting two sweets the same colour Pick 2 e blu ( ) 4/8 = P Pick 1 /9 P(bb) 5/9 x 4/8 = 20/72 + 12/72 = 32/72 5 )= e P(red) = lu 4/8 (b. In this example the P probabilities are affected after 5/8 each sweet is = P( lue) re picked P(b d) = 4/ 9 P(re d) = 3/8 P(br) 5/9 x 4/8 = 20/72 P(rb) 4/9 x 5/8 = 20/72 P(rr) 4/9 x 3/8 = 12/72