Higher Derivatives Concavity 2 nd Derivative Test Lesson

Higher Derivatives Concavity 2 nd Derivative Test Lesson 5. 3

Think About It Just because the price of a stock is increasing … does that make it a good buy? • When might it be a bad buy? What might that have to do with derivatives? 2

Think About It It is important to know the rate of increase! The faster the rate of increase, the better. Suppose a stock price is modeled by • What is the rate of increase for several months in the future? 3

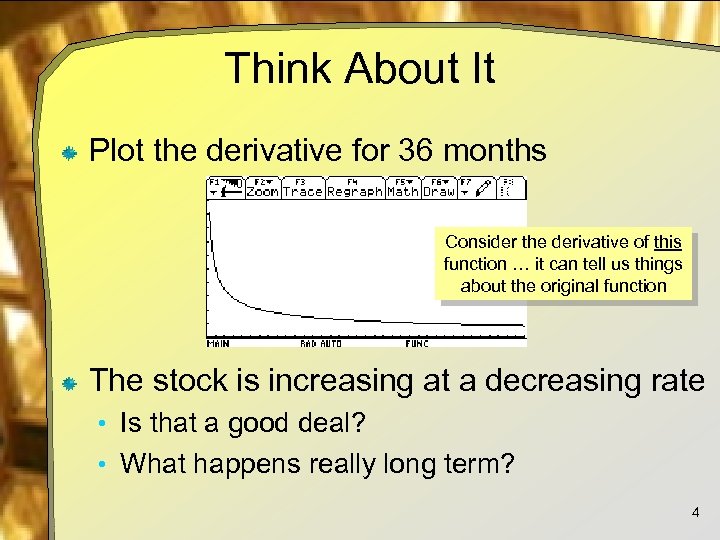Think About It Plot the derivative for 36 months Consider the derivative of this function … it can tell us things about the original function The stock is increasing at a decreasing rate • Is that a good deal? • What happens really long term? 4

Higher Derivatives The derivative of the first derivative is called the second derivative Other notations Third derivative f '''(x), etc. Fourth derivative f (4)(x), etc. 5

Find Some Derivatives Find the second and third derivatives of the following functions 6

Velocity and Acceleration Consider a function which gives a car's distance from a starting point as a function of time The first derivative is the velocity function • The rate of change of distance The second derivative is the acceleration • The rate of change of velocity 7

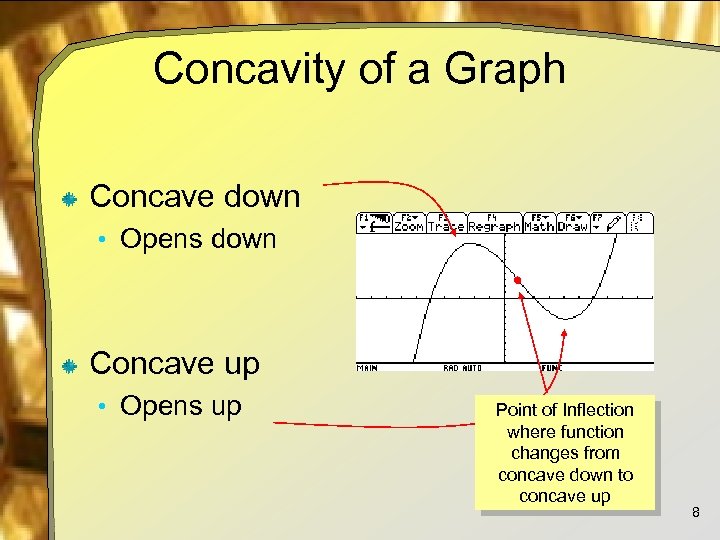Concavity of a Graph Concave down • Opens down Concave up • Opens up Point of Inflection where function changes from concave down to concave up 8

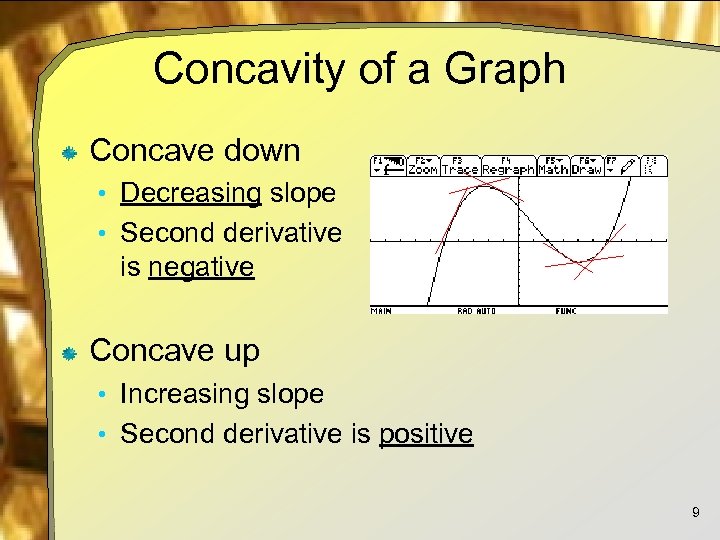Concavity of a Graph Concave down • Decreasing slope • Second derivative is negative Concave up • Increasing slope • Second derivative is positive 9

Test for Concavity Let f be function with derivatives f ' and f '' • Derivatives exist for all points in (a, b) If f ''(x) > 0 for all x in (a, b) • Then f(x) concave up If f ''(x) < 0 for all x in (a, b) • Then f(x) concave down 10

Test for Concavity Strategy Find c where f ''(c) = 0 • This is the test point Check left and right of test point, c • Where f ''(x) < 0, f(x) concave down • Where f ''(x) > 0, f(x) concave up Try it 11

Determining Max or Min Use second derivative test at critical points When f '(c) = 0 … If f ''(c) > 0 • This is a minimum If f ''(c) < 0 • This is a maximum If f ''(c) = 0 • You cannot tell one way or the other! 12

Assignment Lesson 5. 3 Page 345 Exercises 1 – 85 EOO 13