7311a62310042b5a747fd6cdad1561b5.ppt
- Количество слайдов: 43

High-precision atomic physics calculations using a computer algebra system and many-body perturbation theory n Warren F. Perger, Michigan Tech University

Outline n n n n n The many-body problem in physics (a cartoon) Quantum field theory (another cartoon, or two) Need for high-precision atomic theory Many-body perturbation theory (MBPT), atomic physics, and computer algebra systems Feynman diagrammatic reduction (symbolic) Angular algebraic reduction (symbolic) Numerical evaluation of Slater (Rk) integrals Results for a “simple” case Ideas for future development

The Many-body Problem. . . n n Given the initial conditions of n-bodies (objects) at a given time, find the positions, velocities, and other properties at some later time. An example: celestial objects interacting under the force of their mutual gravitational attraction:
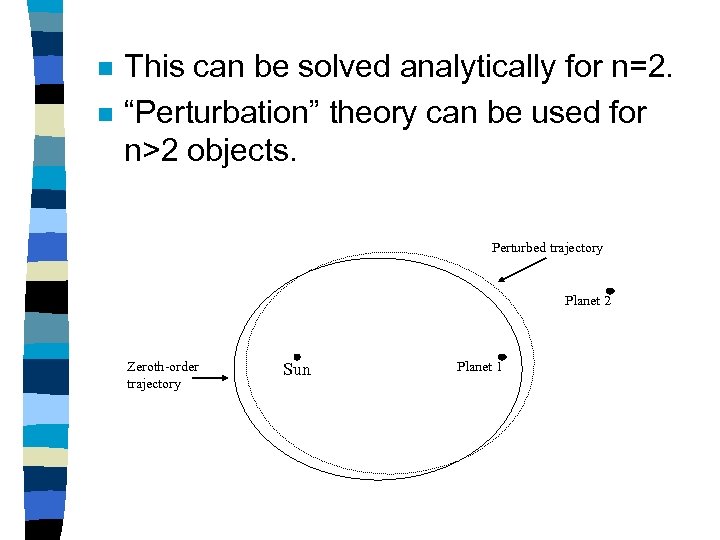
n n This can be solved analytically for n=2. “Perturbation” theory can be used for n>2 objects. Perturbed trajectory Planet 2 Zeroth-order trajectory Sun Planet 1

Why is “high-precision” important? n n Quantum Electrodynamic (QED) effects calculated for hydrogen; Lamb shift of 1057. 70 MHz; Nobel prize, 1965, Tomonaga, Schwinger, Feynman for “Development of QED” Parity nonconservation requires theory < 1% precision to impact development of unified field theories, e. g. SU 2 X U 1

The Atomic System n Requires quantum-mechanical description; solution of the Schroedinger (or Dirac) equation:

Quantum mechanics and perturbation theory n n n Formalism is systematic and well-known. Ability to carry out detailed calculations for an arbitrary system is impractical except for a few simple systems. The symbolic determination of relevant Feynman diagrams offers the possibility of an error-proof, robust, method by using Wick’s theorem [1, 2], which is an alternative to a diagrammatic reduction.

Let: where H 0 = unperturbed Hamiltonian with and

n The wavefunctions are given by: n and the energy expressions by:

n n Representation of the operators, that is the combination of a creation and an annihilation operator, is formally equivalent to the combination of two free lines in a corresponding Feynman (or Goldstone) graph. A few examples of symbolically reducing the terms using Reduce [3] and Mathematica [4, 5, 6]. However, this is but the first, relatively simple, step towards a numeric result which can be compared with experiment.
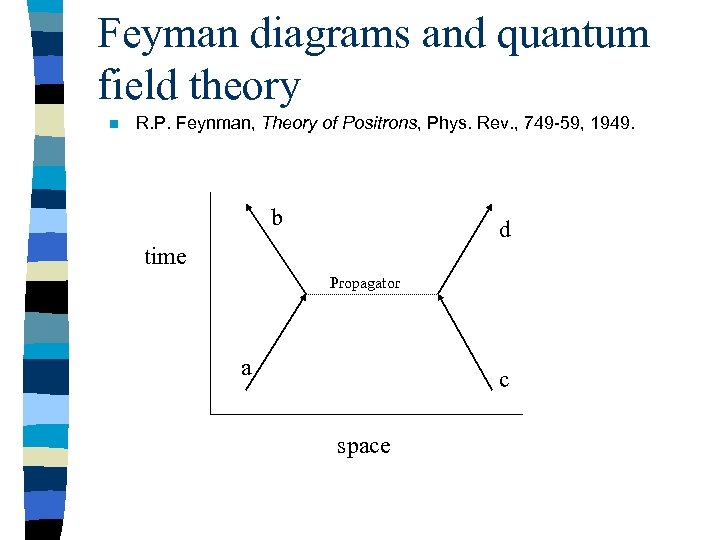
Feyman diagrams and quantum field theory n R. P. Feynman, Theory of Positrons, Phys. Rev. , 749 -59, 1949. b d time Propagator a c space
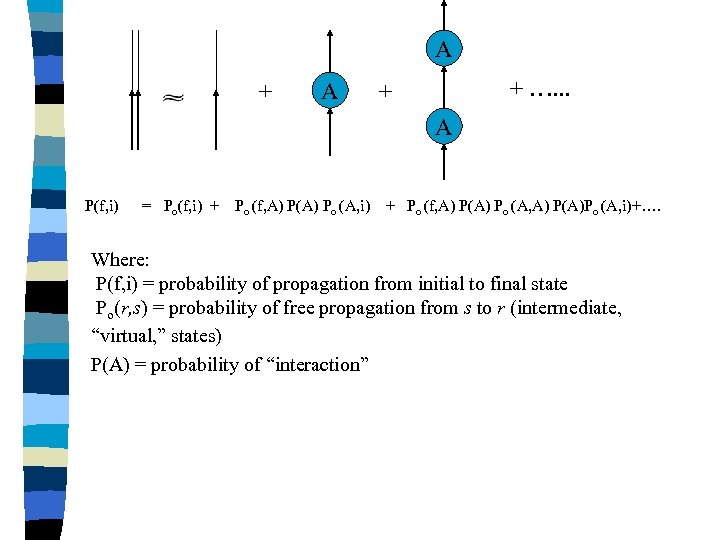
A + …. . . + A P(f, i) = Po(f, i) + Po (f, A) P(A) Po (A, A) P(A)Po (A, i)+…. Where: P(f, i) = probability of propagation from initial to final state Po(r, s) = probability of free propagation from s to r (intermediate, “virtual, ” states) P(A) = probability of “interaction”

Motivation for using Wick’s theorem: multiplication of operator strings (probabilities) |0> is a string of operators acting on the “vacuum”, e. g. , |0> = aa+ |0 c> for the one-particle, zero-hole, case and likewise V is a string of second-quantized operators:

Feynman diagrams and Wick’s theorem Example: Combine two diagrammatic fragments: A=aa+ aa and B= ab+ ab ac+ ad given Wick’s theorem. Then, AB={AB}+{AB} = {aa+ aa ab+ ab ac+ ad } + dac{aa+ ab ad } + dab ab+ ac+ aa ad - dab dac ab+ ad + dac{aa+ ab ac+ ad } + dab ac+ ad n

The role of the computer algebra system n n n Create a data structure capable of handling all attributes of a given list of second-quantized operators: particle or hole, creation or annihilation, core or valence Create routines capable of symbolically performing Wick’s theorem Create routines to reduce to numerically tractable form, typically “Brandow” form Produces results for both energies and transition matrix elements, for open-shell systems and multi-configuration atomic states, using a fully relativistic approach. Example of 1 particle, 0 hole (alkalai’s)

Angular reduction n These “g-functions, ” which carry the many-body effects, along with the bra and ket, must next undergo a reduction into radial and angular parts, typically (again) done with Feynman diagrams specialized for this purpose [7]. But the bra and ket can be each be represented with a Wigner 3 -J symbol, and each g-function with a pair of 3 -J symbols. The angular reduction is performed by using an existing package, Kentaro [8], and a Mathematica routine which finds the minimal angular reduction.

…. …. and…

Symbolic angular reduction n n Once in the form of the product of an arbitrary number of 3 -J (or Clebsch. Gordon) coefficients, Kentaro can be used. A Mathematica “smart wrapper” was developed, in order to assure the minimum angular reduction.
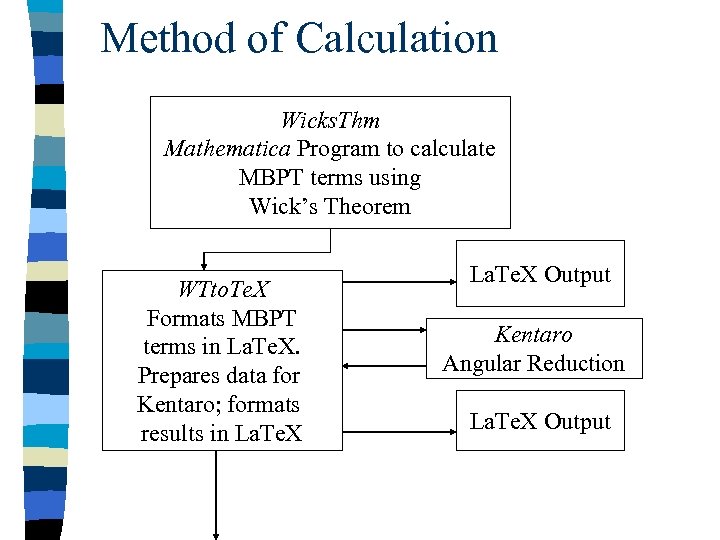
Method of Calculation Wicks. Thm Mathematica Program to calculate MBPT terms using Wick’s Theorem WTto. Te. X Formats MBPT terms in La. Te. X. Prepares data for Kentaro; formats results in La. Te. X Output Kentaro Angular Reduction La. Te. X Output
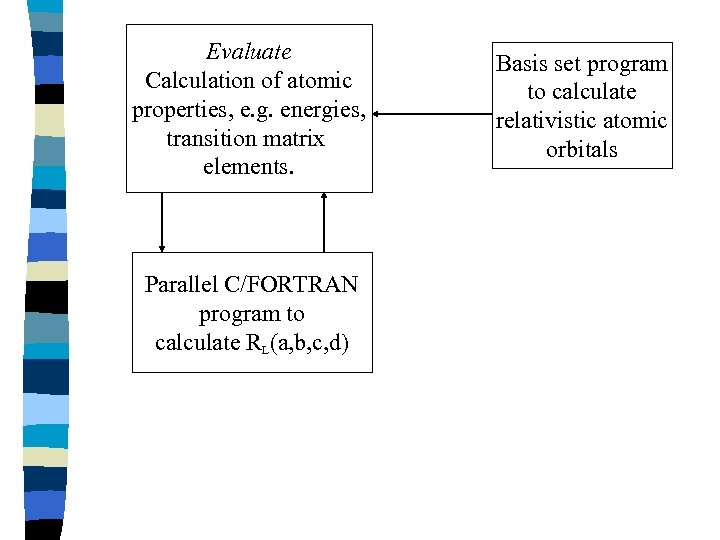
Evaluate Calculation of atomic properties, e. g. energies, transition matrix elements. Parallel C/FORTRAN program to calculate RL(a, b, c, d) Basis set program to calculate relativistic atomic orbitals









How do we know it’s correct? n n n Use software, where possible, to test itself, e. g. calculate E 3 in two ways. Prohibit use of Brandow simplification, then numerically re-calculate and compare. Compare with experiment (last resort).

Parallel processing and Many-body Perturbation Theory (MBPT) n n n MBPT terms can be summed in any order. Terms require a numerical basis set for evaluation. B-splines used to represent orbitals. CPU time on the order of minutes to hours per term. No terms can be left out.

Numerical evaluation n n n Evaluate written in C to exploit pointers ONE subroutine used for all terms (singles, doubles, etc. ) Organization of terms into singles, doubles, etc. facilitates course-grained parallel processing Example of 1 p 0 h illustrates need for parallel processing; quadruple-excitation term requires more time than all other terms combined Client-proxy scheme permits utilization of processors from wide range of locations Heterogeneous collection of computing resources used (SGI Origin 2000, Linux cluster, Sun Solaris)

Total execution time n The total execution time can be estimated as: Where t. RL is the time to evaluate a given Slater integral, N=number of B-splines (~40), n is the order of perturbation theory, and L is the maximum multipole moment (~10). For a 750 MHz Pentium III running Red. Hat Linux 7. 2, this is about 1 ms. Therefore, a second-order energy term takes roughly 402 x 9 x 10 -3 ~ 14 seconds. A quadruples term, however, takes roughly 194 days.

Solutions to the numerical problems 1) 2) Improve on speed of Rk integrals Employ parallel processing.

Improving speed of Rk integrals n B-spline representation is an efficient basis set (Bottcher & Strayer; Notre Dame group) 5 B-splines of 3 rd order (2 nd degree polynomial

n n n n Therefore, Yk(b, d) can be integrated analytically exactly with Mathematica then used to create very efficient Fortran (or C) code 600, 000 lines of Fortran created and compiled Pre-computed Yk(b, d) requires ~ 3 GBytes of memory Re-compiled Linux kernel Running on 64 -bit SGI Origin 2000 With Yk(b, d) pre-computed, results in ~ factor of 400 improvement in speed of Rk integral Must next demonstrate that this rate can be sustained
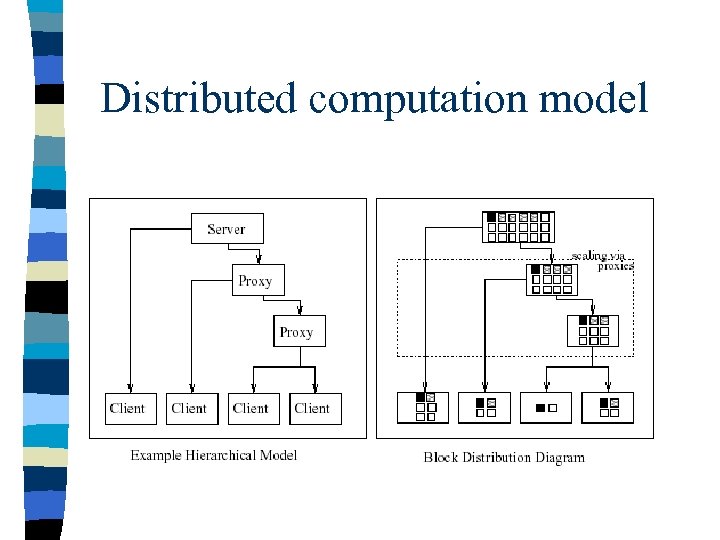
Distributed computation model

n n n Parallel strategy utilizes heterogenous group of machines, across the Internet (cf. Globus) Uses stunnel to prevent malicious intrusion Robust: tested by deliberately stopping either client or host, system recovers automatically, resuming where it left off

Discussion and Results n n n We have achieved a fully integrated approach for symbolically calculating the expressions in MBPT using Mathematica. We have incorporated an automated angular reduction package to further reduce the expressions to a form which can be numerically evaluated. We have written a general-purpose program for numerically evaluating the terms in MBPT for an arbitrary problem up to third-order. We have made numerous consistently checks, such as calculating E(3) two ways and deliberately not combining terms before angular reduction. Rk integral speed shows great improvement. Development of grid-based parallel machine now operational.

Sodium, E(2), S=Single, D=Double, etc. , 40 B-splines, Lmax=9 n E(2) =1. 3578 E-3 (S) -7. 2266 E-3 (D) = -5. 8689 E-3

Sodium, E(3), S=Single, D=Double, etc. , 40 B-splines, Lmax=9

Sodium, Etotal, S=Single, D=Double, etc. , 40 B-splines, Lmax=9 n Etotal = E(0) + E(1) + E(2) + E(3) = -0. 18203269+ 0 -5. 8689 E-3 - 4. 11 E-4 = -0. 18831 n n Eexpt = -0. 18886 (C. E. Moore, Atomic Energy Levels, NBS Circ. No. 35, 1971) Roughly 0. 3% disagreement n Breit/QED corrections not yet included

Future work n n n Refine parallelization strategy Extend to 4 th-order Apply to problems requiring high precision, e. g. Thallium parity violation Testing on many architectures: 32 bit, 64 bit, different compilers… testing and more testing Publish codes; currently “alpha” version
![References n n n n [1] W. F. Perger, et al, Computers in Science References n n n n [1] W. F. Perger, et al, Computers in Science](https://present5.com/presentation/7311a62310042b5a747fd6cdad1561b5/image-43.jpg)
References n n n n [1] W. F. Perger, et al, Computers in Science and Eng. , 3, No 1, 38, Jan/Feb (2001). [2] G. C. Wick, Phys. Rev. 80, 268 (1950). [3] S. A. Blundell, D. S. Guo, W. R. Johnson, and J. Sapirstein, At. Data Nucl. Tables 37, 103 (1987). [4] W. F. Perger, J. Dantuluru, M. Idrees, and K. Flurchick, Proceedings of the 6 th Joint EPS-APS International Conference on Physics Computing, edited by R. Grueber and M. Tomassini (European Physical Society, Geneva, Switzerland, Lugano, Switzerland, 1994), pp. 507 -510. [5] W. Perger, J. Dantuluru, Ken Flurchick, and M. I. Bhatti, in Bulletin of the American Physical Society, APS, Washington, DC, 1995, No. 2, p. 999. [6] W. F. Perger, J. Dantuluru, M. I. Bhatti, and K. Flurchick, in Bulletin of the American Physical Society, Toronto, Canada, 1995, No. 4, p. 1291. [7] I. Lindgren and J. Morrison, Atomic Many-body Theory, Springer-Verlag, 1986. [8] K. Takada, Comput. Phys. Commun. , 69, 142, 1992.
7311a62310042b5a747fd6cdad1561b5.ppt