Скачать презентацию High Performance Analog Integrated Circuit Design The Effect Скачать презентацию High Performance Analog Integrated Circuit Design The Effect

b07d99a84454e628f6f15dd3b5ef7539.ppt

  • Количество слайдов: 67

High Performance Analog Integrated Circuit Design: The Effect of Device Self. Heating on Design High Performance Analog Integrated Circuit Design: The Effect of Device Self. Heating on Design Optimization Ronald L. Carter, Professor Analog Integrated Circuit Design Lab Electrical Engineering Department RLCarter: Analog IC Design with Self Heating The University of Texas at Arlington

Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Models n Effect of Thermal Resistance on Device Biasing n Effect of Thermal Resistance on the Circuit Performance RLCarter: Analog IC n Conclusions/Future Work Design with Self n Heating 2

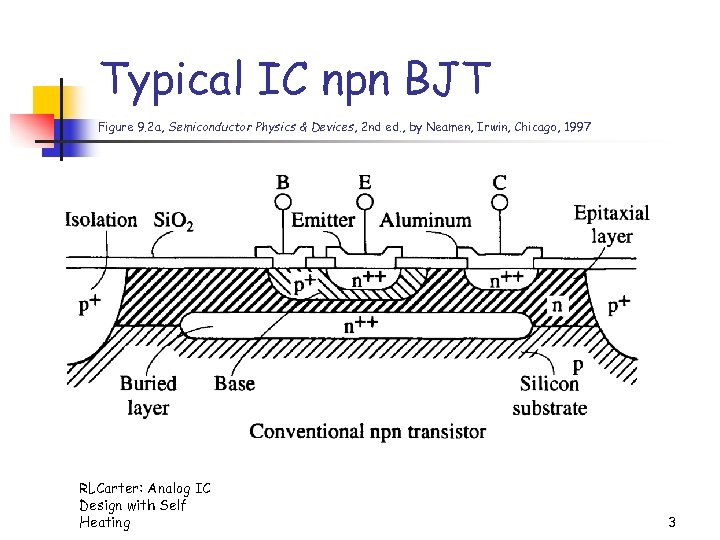Typical IC npn BJT Figure 9. 2 a, Semiconductor Physics & Devices, 2 nd Typical IC npn BJT Figure 9. 2 a, Semiconductor Physics & Devices, 2 nd ed. , by Neamen, Irwin, Chicago, 1997 RLCarter: Analog IC Design with Self Heating 3

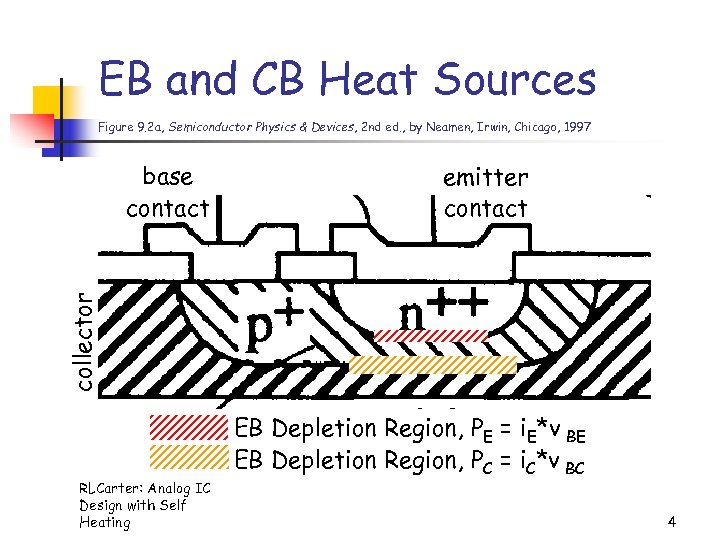EB and CB Heat Sources Figure 9. 2 a, Semiconductor Physics & Devices, 2 EB and CB Heat Sources Figure 9. 2 a, Semiconductor Physics & Devices, 2 nd ed. , by Neamen, Irwin, Chicago, 1997 emitter contact collector base contact RLCarter: Analog IC Design with Self Heating EB Depletion Region, PE = i. E*v BE EB Depletion Region, PC = i. C*v BC 4

Temperature Increase Td-Ta=Ta{[1 + (n+1)( e+ c)/Ta)]1/(n+1)1} e and c are pseudo-temperatures via the Temperature Increase Td-Ta=Ta{[1 + (n+1)( e+ c)/Ta)]1/(n+1)1} e and c are pseudo-temperatures via the Kirchoff transformation, assuming k(T) = k(300 K) [T/300]n n e = RTh, EB |ievbe| n c = RTh, CB |icvbc| n RTh, EB, RTh, CB are thermal res. at Ta. n Following S. H. Whemple, and H. Huang, "Thermal Design of Power Ga. As FETs", in Ga. As FET Principles and RLCarter: Analog ICV. Di. Lorenzo and D. D. Khandelwal, eds. , pp. 313 -347, Artech House, 1982. Technology, J. Design with Self Heating 5

Circuit Simulation of Temperature Effects n n n Typically TNOM (parameter spec. temperature) and Circuit Simulation of Temperature Effects n n n Typically TNOM (parameter spec. temperature) and TEMP (circuit operation temperature) only variables However, Td =Tdevice is a function of ie, vbe, ic and vbc. More flexibility with Vertical Bipolar Inter-Company model (VBIC) RLCarter: Analog IC Design with Self Heating 6

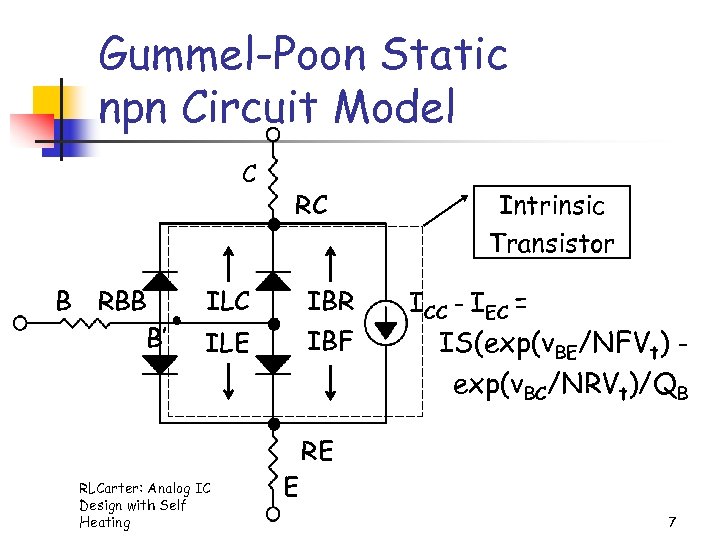Gummel-Poon Static npn Circuit Model C B RBB B’ RC ILC IBR ILE IBF Gummel-Poon Static npn Circuit Model C B RBB B’ RC ILC IBR ILE IBF RLCarter: Analog IC Design with Self Heating E Intrinsic Transistor ICC - IEC = IS(exp(v. BE/NFVt) exp(v. BC/NRVt)/QB RE 7

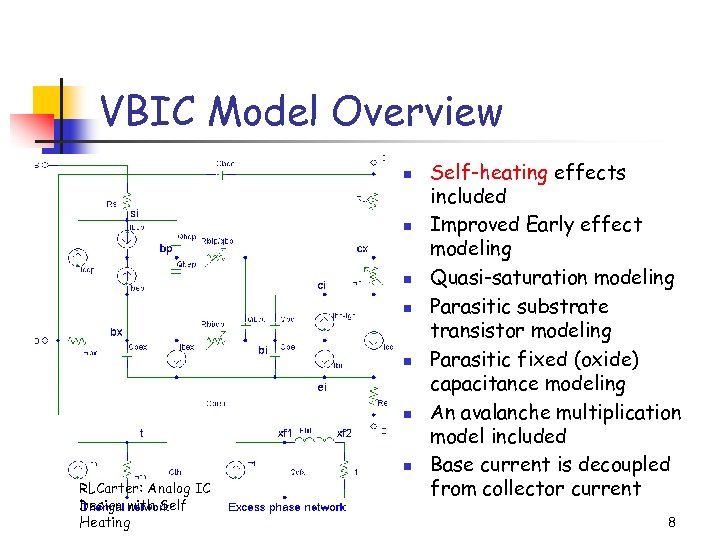VBIC Model Overview n n n n RLCarter: Analog IC Design with Self Heating VBIC Model Overview n n n n RLCarter: Analog IC Design with Self Heating Self-heating effects included Improved Early effect modeling Quasi-saturation modeling Parasitic substrate transistor modeling Parasitic fixed (oxide) capacitance modeling An avalanche multiplication model included Base current is decoupled from collector current 8

CAD Tools Support for VBIC n Hspice ü ü n Does not support PNP CAD Tools Support for VBIC n Hspice ü ü n Does not support PNP device Does not scale with “Area” and “M” terms Spectre ü ü n [4] [5] Support both NPN and PNP devices scale with “Area” and “M” term HPADS ü No temperature nodes (“dt” and “tl”), so unable to simulate thermal coupling effects RLCarter: Analog IC Design with Self Heating 9

Temperature Designations for VBIC Parameters Description Spectre [4] Hspice [5] Name Default Temperature rise Temperature Designations for VBIC Parameters Description Spectre [4] Hspice [5] Name Default Temperature rise of the device from ambient trise 0 dtemp 0 Ambient temperature temp 27 temp 25 Parameters measurement temperature tnom 27 tnom 25 tref 27 RLCarter: Analog IC Design with Self Heating 10

Using VBIC in Spectre [5] Name c b e [s] [dt] [tl] Model. Name Using VBIC in Spectre [5] Name c b e [s] [dt] [tl] Model. Name parameter=value. . . n Selft=1 and Rth>0 to enable Self-heating n 1 volt at the temperature nodes = 1 degree in temperature n “tl” node represents the initial local temperature of device which always corresponds to trise+temp n “dt” node represents the rise above trise+temp caused by thermal dissipation, whose value equals V(dt)-V(tl) n RLCarter: Analog IC Device temperature=V(dt)-V(tl)+trise+temp Design with Self Heating 11

Using VBIC in Cadence n Need explicit external temperature nodes in the symbol to Using VBIC in Cadence n Need explicit external temperature nodes in the symbol to model inter-device thermal coupling by ü ü n Connecting thermal network between “dt” nodes, or Adding VCVS between “tl” and “tlr” node Customized VBIC 6 -terminal (5 -pin) symbol RLCarter: Analog IC Design with Self Heating 12

Model Conversion n n Most BJTs are defined with SGP model A conversion from Model Conversion n n Most BJTs are defined with SGP model A conversion from SGP to VBIC is needed Only approximate conversion is possible Some parameters are unmapped such as Rth and Cth Two approaches are provided ü ü Manual conversion — done empirically and need Local Ratio Evaluation [2] Program conversion using program sgp_2_vbic [3] RLCarter: Analog IC Design with Self Heating 13

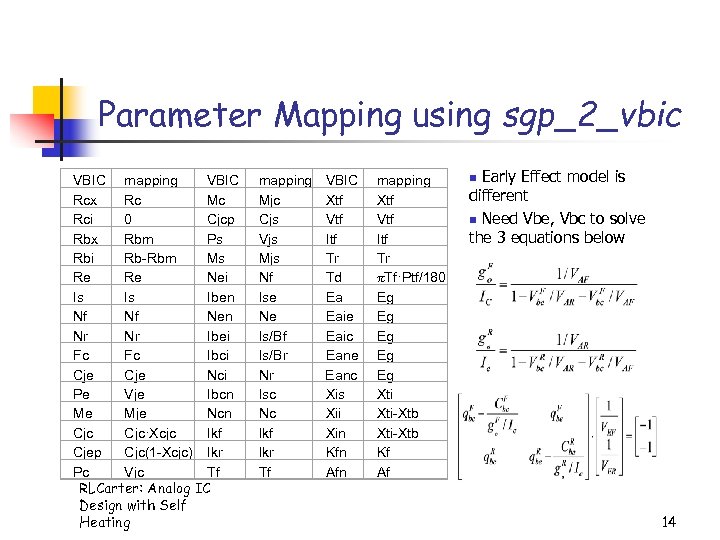Parameter Mapping using sgp_2_vbic VBIC mapping VBIC Rcx Rc Mc Rci 0 Cjcp Rbx Parameter Mapping using sgp_2_vbic VBIC mapping VBIC Rcx Rc Mc Rci 0 Cjcp Rbx Rbm Ps Rbi Rb-Rbm Ms Re Re Nei Is Is Iben Nf Nf Nen Nr Nr Ibei Fc Fc Ibci Cje Nci Pe Vje Ibcn Me Mje Ncn Cjc·Xcjc Ikf Cjep Cjc(1 -Xcjc) Ikr Pc Vjc Tf RLCarter: Analog IC Design with Self Heating mapping Mjc Cjs Vjs Mjs Nf Ise Ne Is/Bf Is/Br Nr Isc Nc Ikf Ikr Tf VBIC Xtf Vtf Itf Tr Td Ea Eaie Eaic Eane Eanc Xis Xii Xin Kfn Afn mapping Xtf Vtf Itf Tr Tf·Ptf/180 Eg Eg Eg Xti-Xtb Kf Af Early Effect model is different n Need Vbe, Vbc to solve the 3 equations below n 14

Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Models n Effect of Thermal Resistance on Device Biasing n Effect of Thermal Resistance on the Circuit Performance RLCarter: Analog IC n Conclusions/Future Work Design with Self n Heating 15

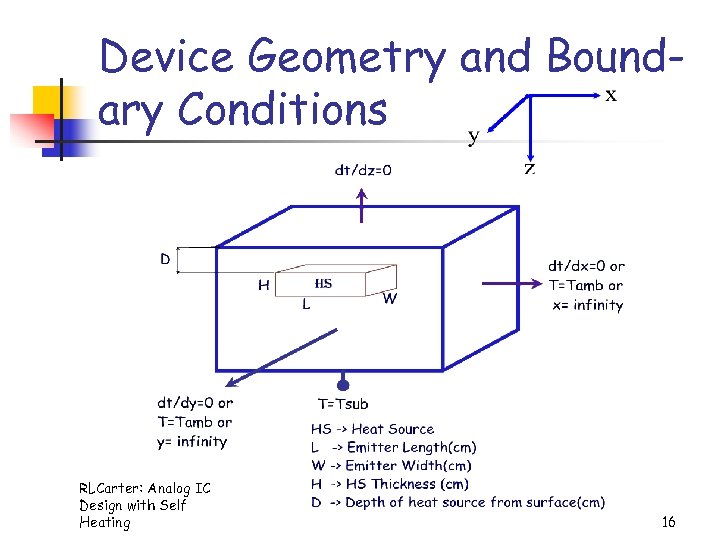Device Geometry and Boundary Conditions RLCarter: Analog IC Design with Self Heating 16 Device Geometry and Boundary Conditions RLCarter: Analog IC Design with Self Heating 16

Static Heat Flow Equation and Poisson’s Equation T = T-T 0 (K) is the Static Heat Flow Equation and Poisson’s Equation T = T-T 0 (K) is the temperature rise above local ambient = Thermal conductivity (Wcm-1 K-1) g= volumetric heat gen. rate (W cm-3) RLCarter: Analog IC dens. , and e = permittivity = charge Design with Self Heating 17

The Electrical Analogy n n n The Kirchoff transformation factors the (T) Both equations The Electrical Analogy n n n The Kirchoff transformation factors the (T) Both equations become the Laplacian V[Volt] is the analog of T[K] I[Ampere] is the analog of P [Watts] V = IR is the analog of T = P RTH RLCarter: Analog IC Design with Self Heating 18

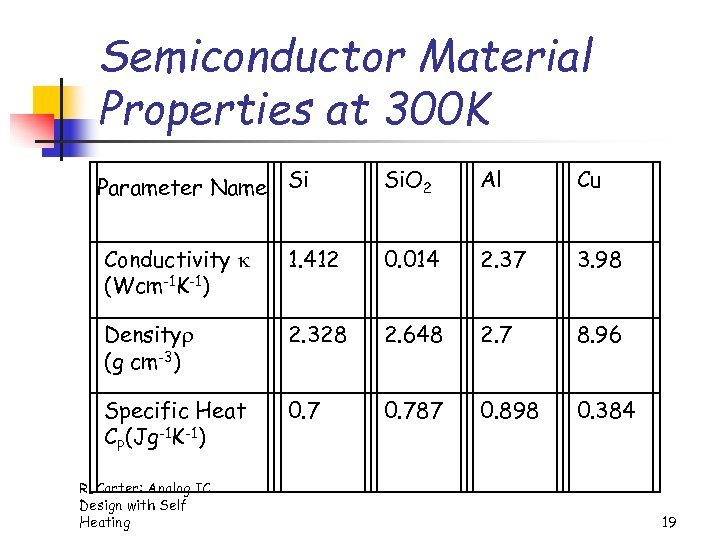Semiconductor Material Properties at 300 K Parameter Name Si Si. O 2 Al Cu Semiconductor Material Properties at 300 K Parameter Name Si Si. O 2 Al Cu Conductivity (Wcm-1 K-1) 1. 412 0. 014 2. 37 3. 98 Density (g cm-3) 2. 328 2. 648 2. 7 8. 96 Specific Heat CP(Jg-1 K-1) 0. 787 0. 898 0. 384 RLCarter: Analog IC Design with Self Heating 19

Applying the Analogy to Spreading Resistance The potential field due to a point current Applying the Analogy to Spreading Resistance The potential field due to a point current source on a wafer surface is V = I/(2 r) The thermal analogy is T = P/(2 r) For a cylindrical contact of radius r, the spreading resistance, Rsp = /4 r The thermal analogy is Rth = 1/4 r Dieter Analog IC RLCarter: K. Schroder, “Semiconductor material and device characterization, 2 nd Ed. , Wiley-Interscience in 1998, New York Pages 31 -33. Design with Self Heating 20

Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Models n Effect of Thermal Resistance on Device Biasing n Effect of Thermal Resistance on the Circuit Performance RLCarter: Analog IC n Conclusions/Future Work Design with Self n Heating 21

Thermal Resistance Model for square emitter n For a square emitter of side w Thermal Resistance Model for square emitter n For a square emitter of side w S. H. Whemple, IC RLCarter: Analogand H. Huang, op. cit. Design with Self Heating 22

Image effect of Heat Sources Below Surface emitter contact D collector base contact EB Image effect of Heat Sources Below Surface emitter contact D collector base contact EB Depletion Region, PE = i. E*v BE EB Depletion Region, PC = i. C*v BC RLCarter: Analog IC Design with Self Heating 23

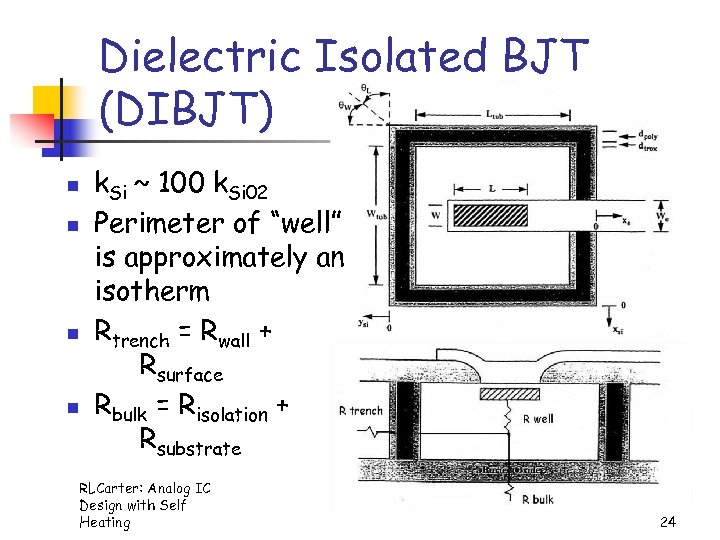Dielectric Isolated BJT (DIBJT) n n k. Si ~ 100 k. Si 02 Perimeter Dielectric Isolated BJT (DIBJT) n n k. Si ~ 100 k. Si 02 Perimeter of “well” is approximately an isotherm Rtrench = Rwall + Rsurface Rbulk = Risolation + Rsubstrate RLCarter: Analog IC Design with Self Heating 24

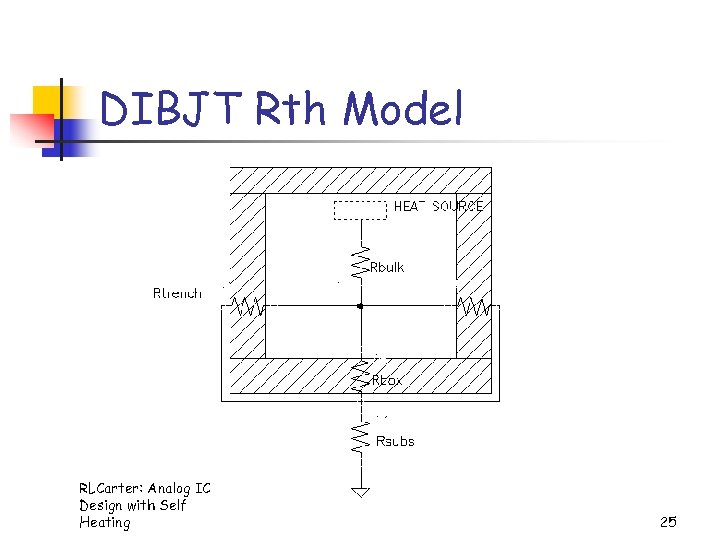DIBJT Rth Model RLCarter: Analog IC Design with Self Heating 25 DIBJT Rth Model RLCarter: Analog IC Design with Self Heating 25

Analogy Modeling of Device Thermal Resistance RLCarter: Analog IC Design with Self Heating 26 Analogy Modeling of Device Thermal Resistance RLCarter: Analog IC Design with Self Heating 26

Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Models n Effect of Thermal Resistance on Device Biasing n Effect of Thermal Resistance on the Circuit Performance RLCarter: Analog IC n Conclusions/Future Work Design with Self n Heating 27

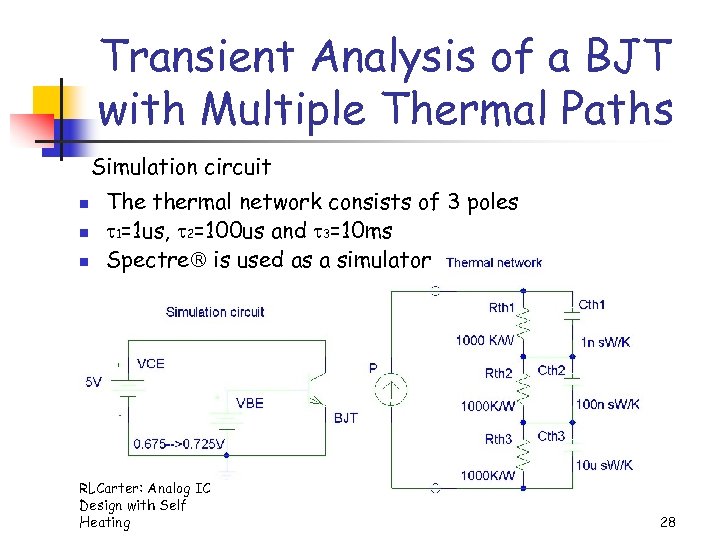Transient Analysis of a BJT with Multiple Thermal Paths Simulation circuit n n n Transient Analysis of a BJT with Multiple Thermal Paths Simulation circuit n n n The thermal network consists of 3 poles 1=1 us, 2=100 us and 3=10 ms Spectre is used as a simulator RLCarter: Analog IC Design with Self Heating 28

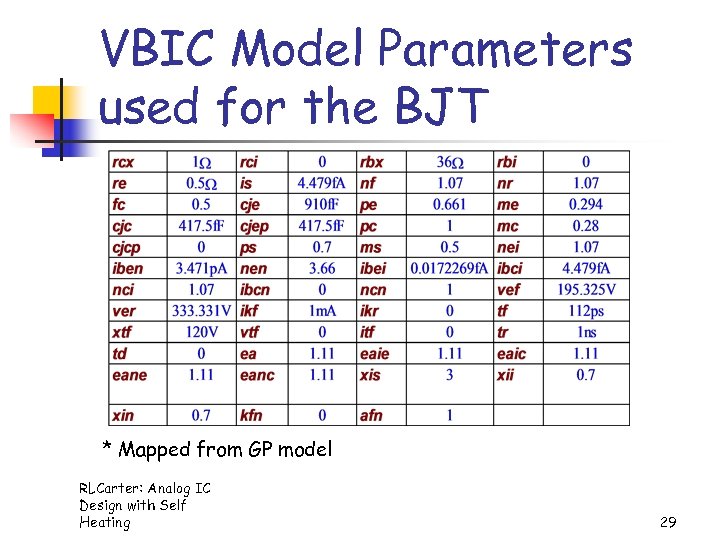VBIC Model Parameters used for the BJT * Mapped from GP model RLCarter: Analog VBIC Model Parameters used for the BJT * Mapped from GP model RLCarter: Analog IC Design with Self Heating 29

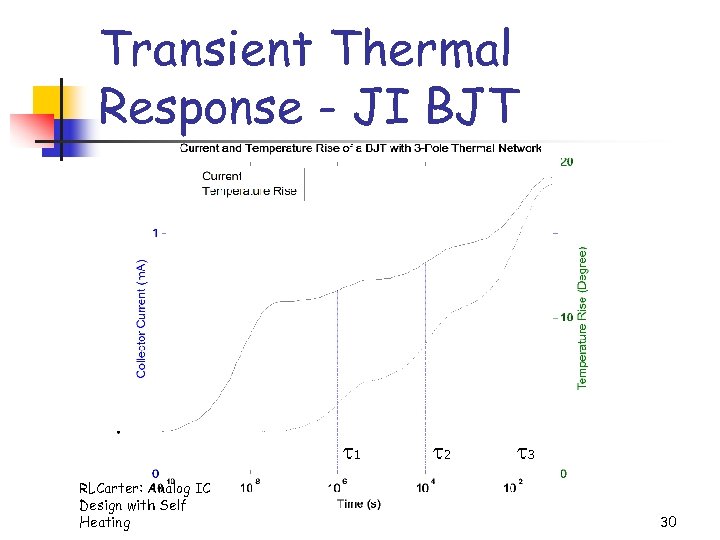Transient Thermal Response - JI BJT 1 RLCarter: Analog IC Design with Self Heating Transient Thermal Response - JI BJT 1 RLCarter: Analog IC Design with Self Heating 2 3 30

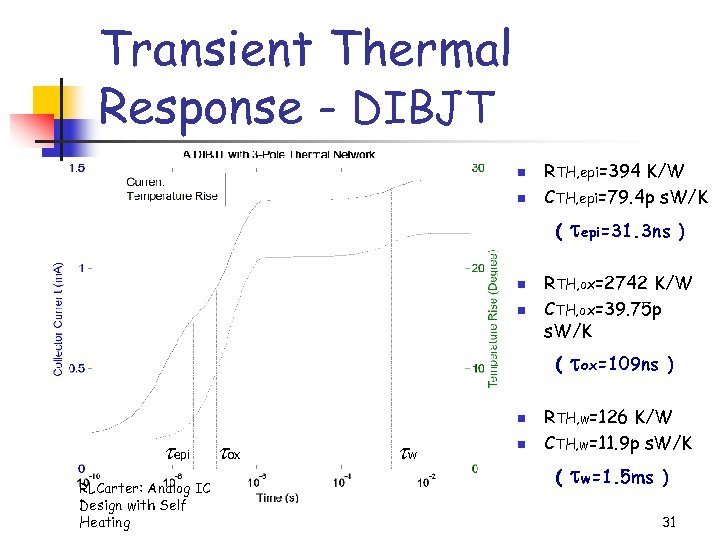Transient Thermal Response - DIBJT n n RTH, epi=394 K/W CTH, epi=79. 4 p Transient Thermal Response - DIBJT n n RTH, epi=394 K/W CTH, epi=79. 4 p s. W/K ( n n epi RLCarter: Analog IC Design with Self Heating ox w n ) RTH, ox=2742 K/W CTH, ox=39. 75 p s. W/K ( n epi=31. 3 ns ox=109 ns ) RTH, w=126 K/W CTH, w=11. 9 p s. W/K ( w=1. 5 ms ) 31

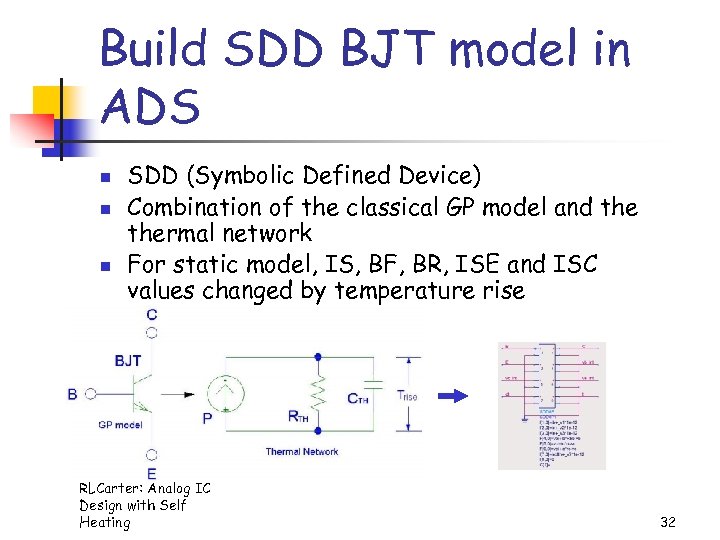Build SDD BJT model in ADS n n n SDD (Symbolic Defined Device) Combination Build SDD BJT model in ADS n n n SDD (Symbolic Defined Device) Combination of the classical GP model and thermal network For static model, IS, BF, BR, ISE and ISC values changed by temperature rise RLCarter: Analog IC Design with Self Heating 32

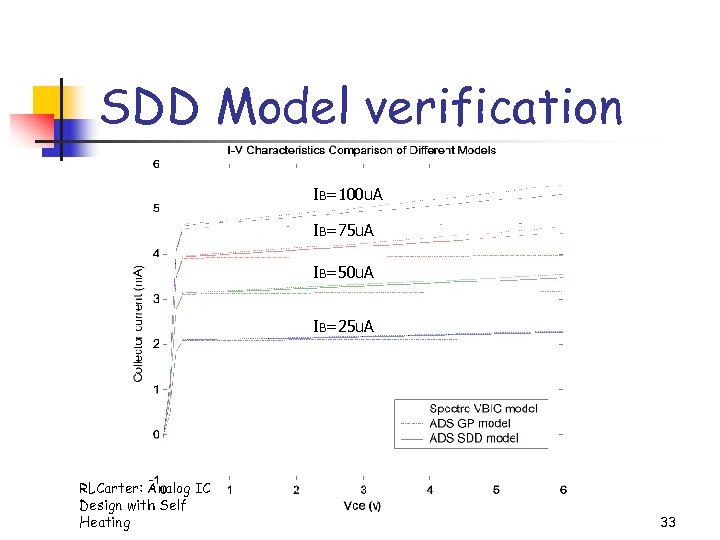SDD Model verification IB=100 u. A IB=75 u. A IB=50 u. A IB=25 u. SDD Model verification IB=100 u. A IB=75 u. A IB=50 u. A IB=25 u. A RLCarter: Analog IC Design with Self Heating 33

Current Mirror Driving BJT with 3 Emitter Fingers n n Simulation Circuit IC 1 Current Mirror Driving BJT with 3 Emitter Fingers n n Simulation Circuit IC 1 IC 2 IC 3 n n cme cee RLCarter: Analog IC Design with Self Heating n The multiple finger BJT consists of 3 fingers, Q 1, Q 2 and Q 3. They have the same geometrical size with Qref Q 2 is the inner finger Thermal coupling occurs between 3 fingers. The coupling factor is Cme and Cee No thermal coupling between the multiply finger BJT and Qref 34

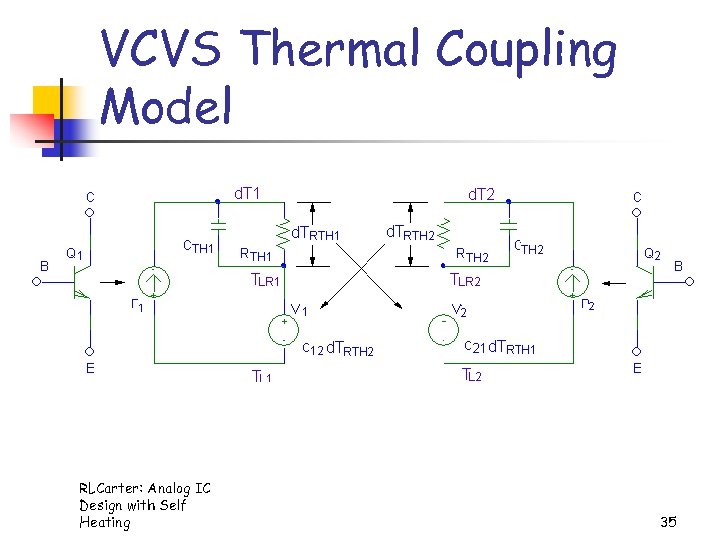VCVS Thermal Coupling Model RLCarter: Analog IC Design with Self Heating 35 VCVS Thermal Coupling Model RLCarter: Analog IC Design with Self Heating 35

Model Parameters * Typical values for 1 um 2 um device RLCarter: Analog IC Model Parameters * Typical values for 1 um 2 um device RLCarter: Analog IC Design with Self Heating 36

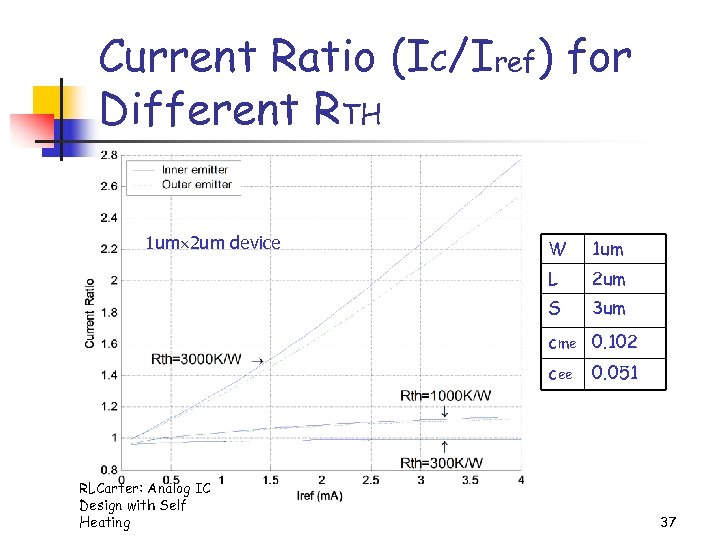Current Ratio (IC/Iref) for Different RTH 1 um 2 um device W 1 um Current Ratio (IC/Iref) for Different RTH 1 um 2 um device W 1 um L 2 um S 3 um cme 0. 102 cee RLCarter: Analog IC Design with Self Heating 0. 051 37

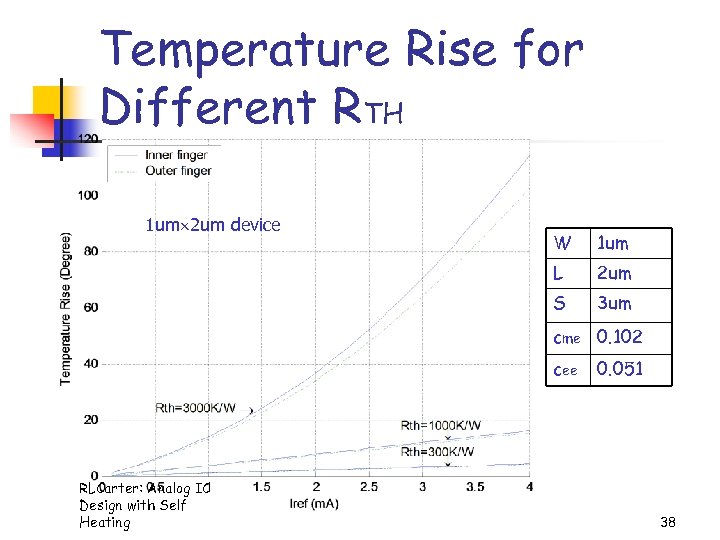Temperature Rise for Different RTH 1 um 2 um device W 1 um L Temperature Rise for Different RTH 1 um 2 um device W 1 um L 2 um S 3 um cme 0. 102 cee RLCarter: Analog IC Design with Self Heating 0. 051 38

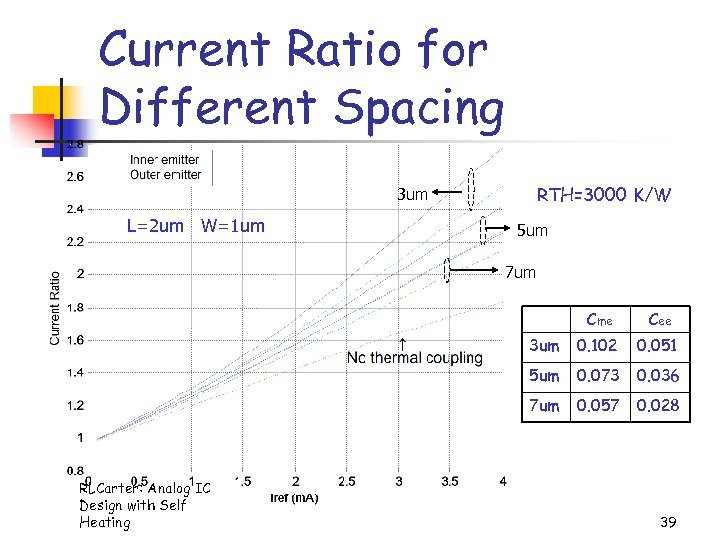Current Ratio for Different Spacing RTH=3000 K/W 3 um L=2 um W=1 um 5 Current Ratio for Different Spacing RTH=3000 K/W 3 um L=2 um W=1 um 5 um 7 um Cme 3 um 0. 102 0. 051 5 um 0. 073 0. 036 7 um RLCarter: Analog IC Design with Self Heating Cee 0. 057 0. 028 39

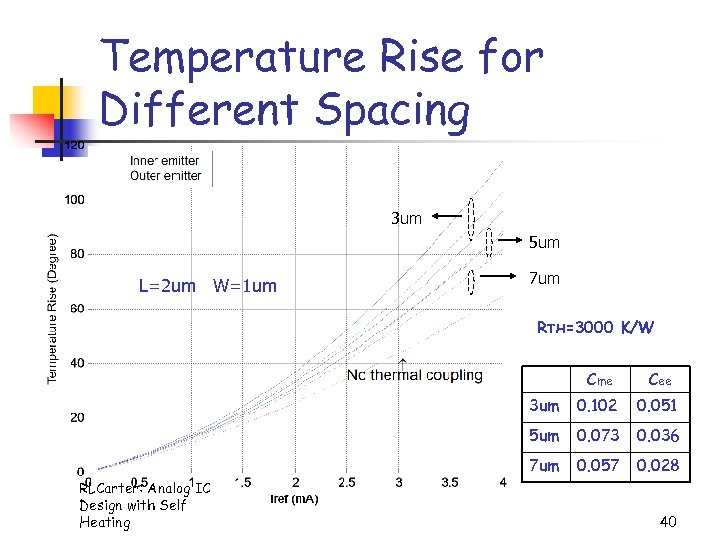Temperature Rise for Different Spacing 3 um 5 um L=2 um W=1 um 7 Temperature Rise for Different Spacing 3 um 5 um L=2 um W=1 um 7 um RTH=3000 K/W Cme 3 um 0. 102 0. 051 5 um 0. 073 0. 036 7 um RLCarter: Analog IC Design with Self Heating Cee 0. 057 0. 028 40

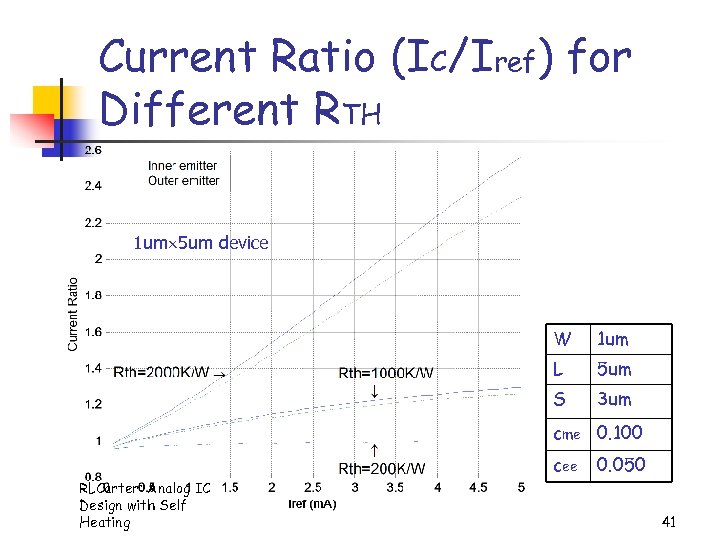Current Ratio (IC/Iref) for Different RTH 1 um 5 um device W 1 um Current Ratio (IC/Iref) for Different RTH 1 um 5 um device W 1 um L 5 um S 3 um cme 0. 100 cee RLCarter: Analog IC Design with Self Heating 0. 050 41

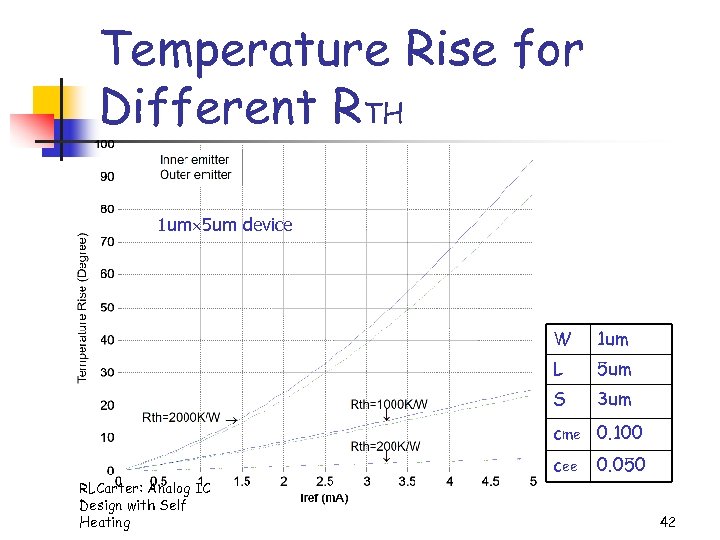Temperature Rise for Different RTH 1 um 5 um device W 1 um L Temperature Rise for Different RTH 1 um 5 um device W 1 um L 5 um S 3 um cme 0. 100 cee RLCarter: Analog IC Design with Self Heating 0. 050 42

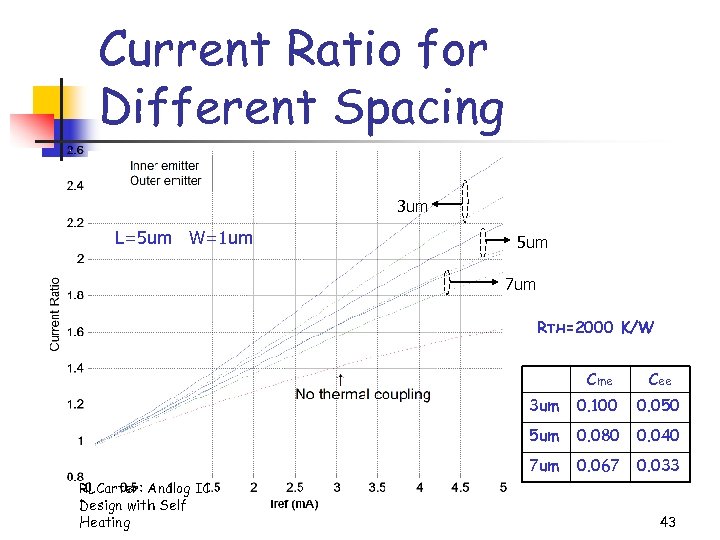Current Ratio for Different Spacing 3 um L=5 um W=1 um 5 um 7 Current Ratio for Different Spacing 3 um L=5 um W=1 um 5 um 7 um RTH=2000 K/W Cme 3 um 0. 100 0. 050 5 um 0. 080 0. 040 7 um RLCarter: Analog IC Design with Self Heating Cee 0. 067 0. 033 43

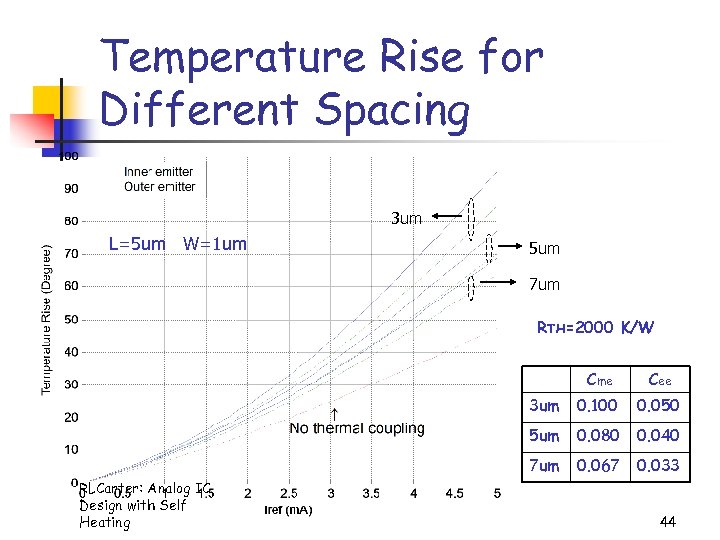Temperature Rise for Different Spacing 3 um L=5 um W=1 um 5 um 7 Temperature Rise for Different Spacing 3 um L=5 um W=1 um 5 um 7 um RTH=2000 K/W Cme 3 um 0. 100 0. 050 5 um 0. 080 0. 040 7 um RLCarter: Analog IC Design with Self Heating Cee 0. 067 0. 033 44

Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Models n Effect of Thermal Resistance on Device Biasing n Effect of Thermal Resistance on the Circuit Performance RLCarter: Analog IC n Conclusions/Future Work Design with Self n Heating 45

A 741 Simulation Simulated by Spectre (Ver. 4. 4. 6. 061301) n Analog A 741 Simulation Simulated by Spectre (Ver. 4. 4. 6. 061301) n Analog Waveform is used to obtain graphic output n Use the circuit posted on WEB (http: //wwwee. uta. edu/Online/adavis/analog/f_opamp. cir) n Transistor models are mapped to VBIC model using sgp_2_vbic (only one npn and pnp model used) n Area of Q 13 A is 0. 25; Area of Q 13 B is 0. 75 n Areas of Q 14 and Q 20 are 3 n Areas of other transistors are 1 n Connect A 741 with 15 V voltage supplies RLCarter: Analog IC n Design with Self Heating 46

μA 741 Op-Amp Schematic RLCarter: Analog IC Design with Self Heating [1] 47 μA 741 Op-Amp Schematic RLCarter: Analog IC Design with Self Heating [1] 47

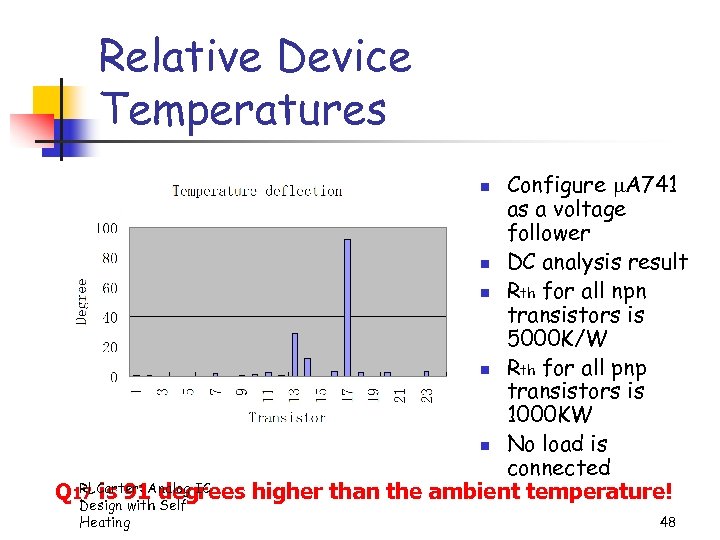Relative Device Temperatures Configure A 741 as a voltage follower n DC analysis result Relative Device Temperatures Configure A 741 as a voltage follower n DC analysis result n Rth for all npn transistors is 5000 K/W n Rth for all pnp transistors is 1000 KW n No load is connected RLCarter: degrees higher than the ambient temperature! Q 17 is 91 Analog IC Design with Self n Heating 48

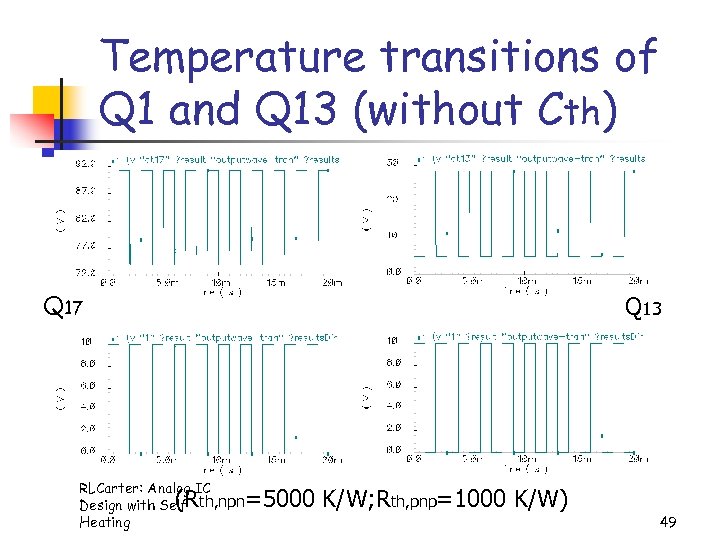Temperature transitions of Q 1 and Q 13 (without Cth) Q 17 Q 13 Temperature transitions of Q 1 and Q 13 (without Cth) Q 17 Q 13 RLCarter: Analog IC Design with Self th, npn Heating (R =5000 K/W; Rth, pnp=1000 K/W) 49

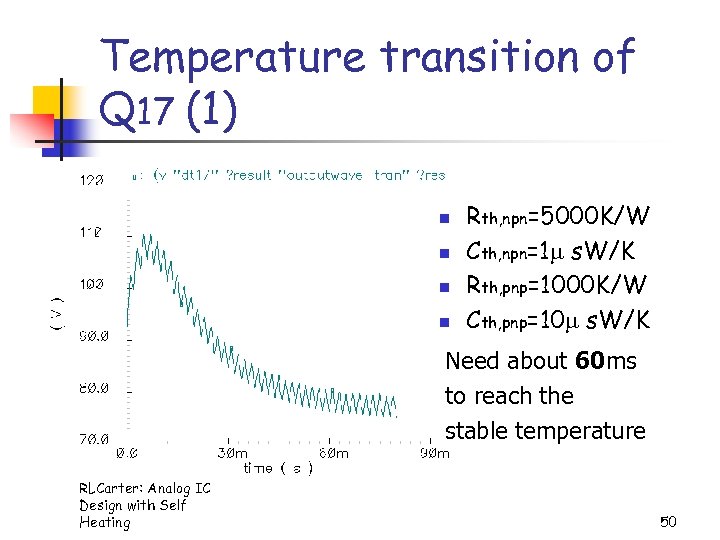Temperature transition of Q 17 (1) n n Rth, npn=5000 K/W Cth, npn=1 s. Temperature transition of Q 17 (1) n n Rth, npn=5000 K/W Cth, npn=1 s. W/K Rth, pnp=1000 K/W Cth, pnp=10 s. W/K Need about 60 ms to reach the stable temperature RLCarter: Analog IC Design with Self Heating 50

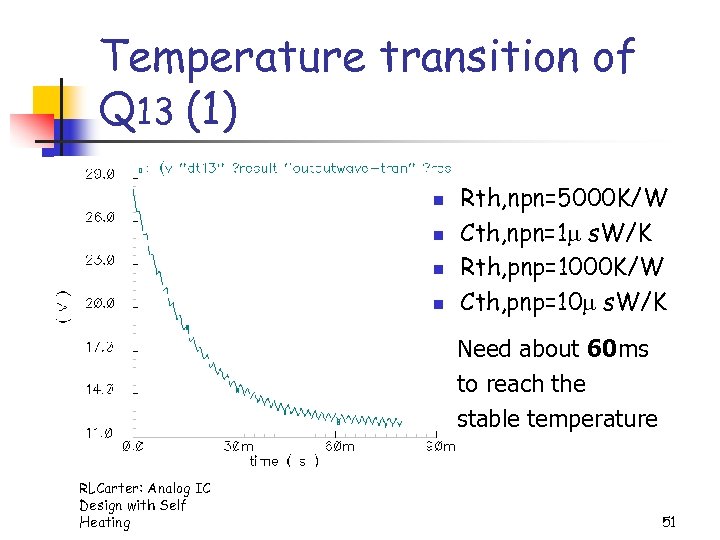Temperature transition of Q 13 (1) n n Rth, npn=5000 K/W Cth, npn=1 s. Temperature transition of Q 13 (1) n n Rth, npn=5000 K/W Cth, npn=1 s. W/K Rth, pnp=1000 K/W Cth, pnp=10 s. W/K Need about 60 ms to reach the stable temperature RLCarter: Analog IC Design with Self Heating 51

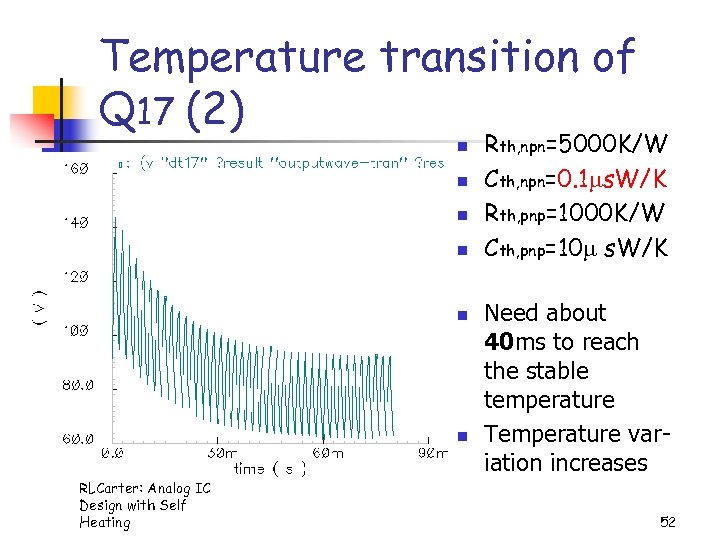Temperature transition of Q 17 (2) n n n RLCarter: Analog IC Design with Temperature transition of Q 17 (2) n n n RLCarter: Analog IC Design with Self Heating Rth, npn=5000 K/W Cth, npn=0. 1 s. W/K Rth, pnp=1000 K/W Cth, pnp=10 s. W/K Need about 40 ms to reach the stable temperature Temperature variation increases 52

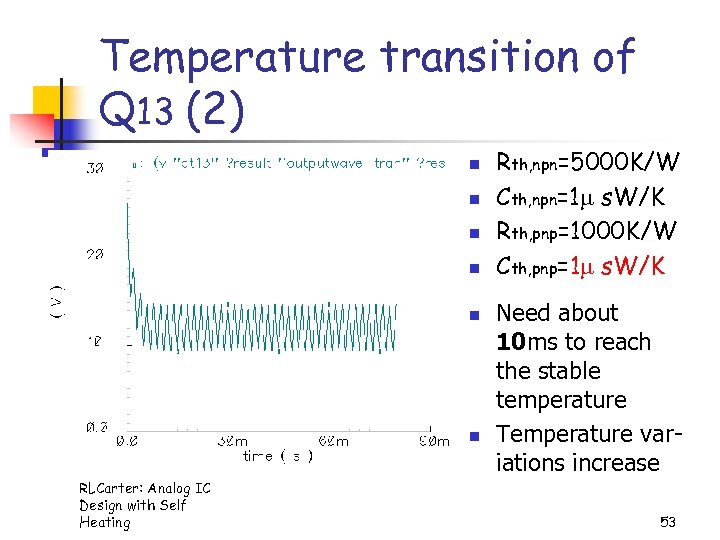Temperature transition of Q 13 (2) n n n RLCarter: Analog IC Design with Temperature transition of Q 13 (2) n n n RLCarter: Analog IC Design with Self Heating Rth, npn=5000 K/W Cth, npn=1 s. W/K Rth, pnp=1000 K/W Cth, pnp=1 s. W/K Need about 10 ms to reach the stable temperature Temperature variations increase 53

Circuit used to measure the open loop gain[2] Simulation parameters: n n n Use Circuit used to measure the open loop gain[2] Simulation parameters: n n n Use a feedback technique to determine the open loop gain DUT is the op amp to be tested Nulling op amp is connected in a feedback mode RLCarter: Analog IC Design with Self Heating n n n R 1=100 R 2=1 M R 3=1 K Vmid=0 VSRC 1 sweeps from 0 to 1 V 54

Typical simulation output RLCarter: Analog IC Design with Self Heating 55 Typical simulation output RLCarter: Analog IC Design with Self Heating 55

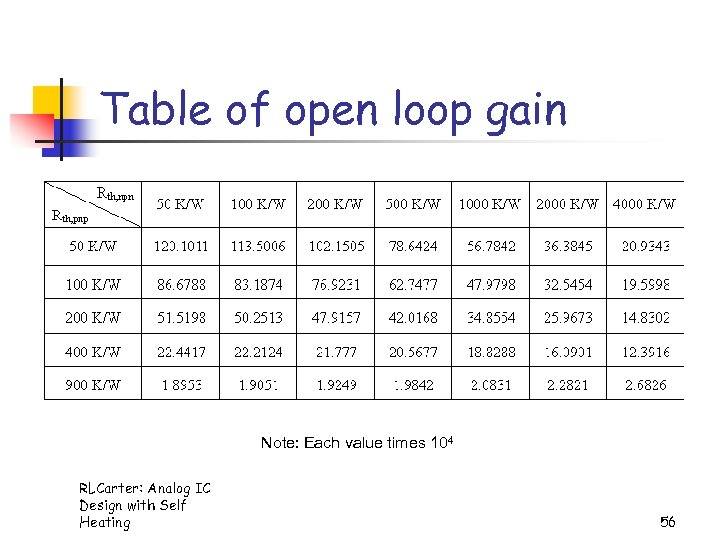Table of open loop gain Note: Each value times 104 RLCarter: Analog IC Design Table of open loop gain Note: Each value times 104 RLCarter: Analog IC Design with Self Heating 56

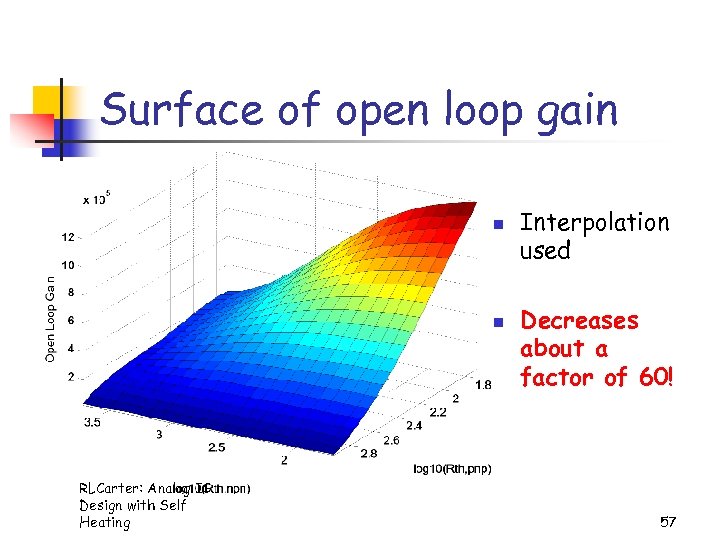Surface of open loop gain n n RLCarter: Analog IC Design with Self Heating Surface of open loop gain n n RLCarter: Analog IC Design with Self Heating Interpolation used Decreases about a factor of 60! 57

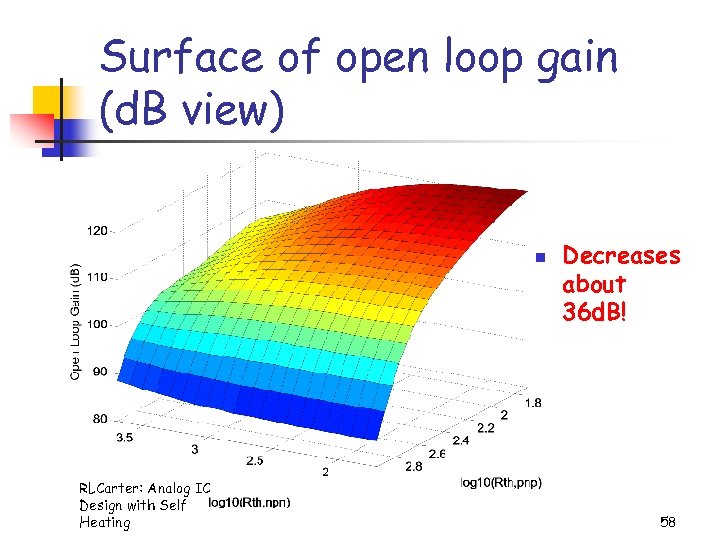Surface of open loop gain (d. B view) n RLCarter: Analog IC Design with Surface of open loop gain (d. B view) n RLCarter: Analog IC Design with Self Heating Decreases about 36 d. B! 58

Slew rate (without Cth ) n n Voltage follower is used Input signal n Slew rate (without Cth ) n n Voltage follower is used Input signal n n 5 K pulse input rise and fall time: 1 S RLCarter: Analog IC Design with Self Heating n n n Voltage level: 0 and 10 V Rising edge is measured Unit: V/ S Only 2% variation 59

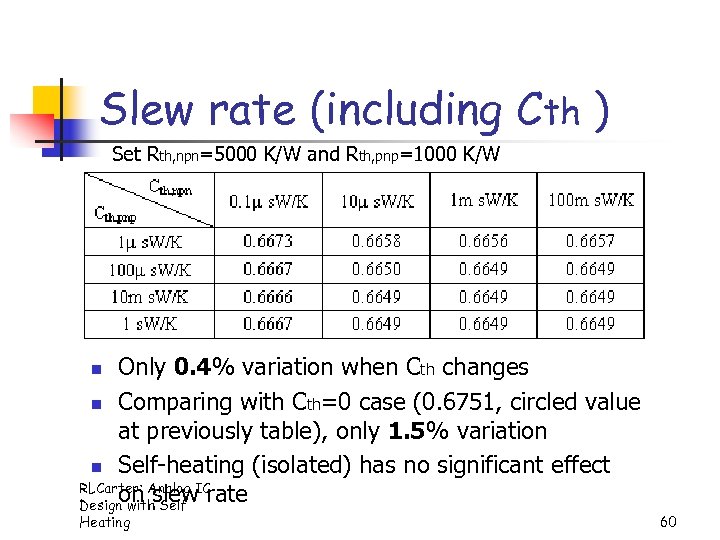Slew rate (including Cth ) Set Rth, npn=5000 K/W and Rth, pnp=1000 K/W Only Slew rate (including Cth ) Set Rth, npn=5000 K/W and Rth, pnp=1000 K/W Only 0. 4% variation when Cth changes n Comparing with Cth=0 case (0. 6751, circled value at previously table), only 1. 5% variation n Self-heating (isolated) has no significant effect RLCarter: Analog IC on slew rate Design with Self n Heating 60

Thermal coupling effect on open-loop gain n n Use the same circuit discussed previously Thermal coupling effect on open-loop gain n n Use the same circuit discussed previously Set Rth, npn=4000 K/W and Rth, pnp=900 K/W and Cth, npn=Cth, pnp=0 The hottest transistor is Q 17 The amplificatory transistors at 1 st stage are Q 3 and Q 4 Temperature node of Q 17 is connected with temperature node of Q 3 and Q 4 by two identical thermal resistors RC RLCarter: Analog IC Design with Self Heating 61

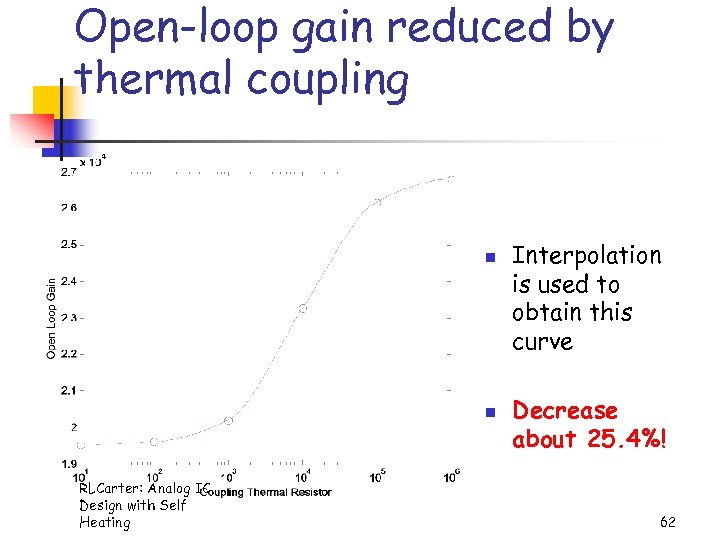Open-loop gain reduced by thermal coupling n n RLCarter: Analog IC Design with Self Open-loop gain reduced by thermal coupling n n RLCarter: Analog IC Design with Self Heating Interpolation is used to obtain this curve Decrease about 25. 4%! 62

Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Analog IC Design with Self-Heating Heat Source/Temperature Effects n Thermal Equations/Analogy n Thermal Resistance Models n Effect of Thermal Resistance on Device Biasing n Effect of Thermal Resistance on the Circuit Performance RLCarter: Analog IC n Conclusions/Future Work Design with Self n Heating 63

Summary n VBIC model used to analyze thermal effects n n n Isolated self-heating Summary n VBIC model used to analyze thermal effects n n n Isolated self-heating in A 741 n n n Effect of individual device temperatures in a A 741 Inter-device heating effects Isolated self-heating can reduce the open loop gain Not a significant change in slew rate Preliminary study on thermal coupling effect n n Open loop gain is reduced if significant thermal coupling exists between 1 st and 2 nd stage Current mirror temperature compensation schemes are more critical when coupling is not optimum. RLCarter: Analog IC Design with Self Heating 64

Acknowledgements: Support n n n The. Texas Higher Education Coordinating Board (THECB) National Semiconductor Acknowledgements: Support n n n The. Texas Higher Education Coordinating Board (THECB) National Semiconductor Corporation (NSC) The National Science Foundation Industry/University Center for Electronic Materials, Devices and Systems (NSF/CEMDAS) RLCarter: Analog IC Design with Self Heating 65

Acknowledgements: Analog IC Research Group n n n n Professor W. Alan Davis Zhipeng Acknowledgements: Analog IC Research Group n n n n Professor W. Alan Davis Zhipeng Zhu Zheng Li Siddharth Nashiney Naveen Kumar Reddy Siddareddygari Shankaranarayanan Rajaraman Piyush Thacker Anurag Lakhlani RLCarter: Analog IC Design with Self Heating 66

References Paul R. Gray, Robert G. Meyer, et al, Analysis and design of analog References Paul R. Gray, Robert G. Meyer, et al, Analysis and design of analog integrated circuits, New York: Wiley, c 2001 Fujiang Lin, et al, “Extraction Of VBIC Model for Si. Ge HBTs Made Easy by Going Through Gummel-Poon Model”, from http: //eesof. tm. agilent. com/pdf/VBIC_Model_Extraction. pdf http: //www. fht-esslingen. de/institute/iafgp/neu/VBIC/ Avanti Star-spice User Manual, 04, 2001. Affirma Spectre Circuit Simulator Device Model Equations Zweidinger, D. T. ; Fox, R. M. , et al, “Equivalent circuit modeling of static substrate thermal coupling using VCVS representation”, Solid-State Circuits, IEEE Journal of , Volume: 2 Issue: 9 , Sept. 2002, Page(s): 1198 -1206 Jonathan S. Brodsky, “Physics based impedance models for the simulation of self-heating in semiconductor devices and circuits”, Ph. D Dissertation, Dept of Electrical and Computer Engineering, University of Florida, Gainesville, Aug 1997. Mc. Andrew, C. , Seitchik, J. and etal, ” VBIC 95: An improved vertical, IC bipolar transistor model”, Bipolar/Bi. CMOS Circuits and Technology Meeting, 1995. , Proceedings of the 1995 Burns and Robert, An introduction to mixed-signal testing, Oxford University Press, 1999 Copyright Texas Instruments RLCarter: Analog IC Design with Self Heating 67