Hi PC 2002 12 19 2002 x S-systems

Hi. PC 2002 12 19 2002 x. S-systems: e. Xtended S-systems & Algebraic Differential Automata for Modeling Cellular Behavior ¦ Bud Mishra Professor (Cold Spring Harbor Laboratory) Professor of CS & Mathematics (Courant, NYU) With M. Antoniotti, A. Policriti and N. Ugel 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 1

Why Systems Biology? • It is not uncommon to assume certain biological problems to have achieved a cognitive finality without rigorous justification. • Rigorous mathematical models with automated tools for reasoning, simulation, and computation can be of enormous help to uncover – cognitive flaws, – qualitative simplification or – overly generalized assumptions. • Some ideal candidates for such study would include: – – prion hypothesis cell cycle machinery muscle contractility processes involved in cancer (cell cycle regulation, angiogenesis, DNA repair, apoptosis, cellular senescence, tissue space modeling enzymes, etc. ) – signal transduction pathways, and many others. 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 2

Systems Biology Combining the mathematical rigor of numerology with the predictive power of astrology. Cyberia Numerlogy SYSTEMS BIOLOGY The Astrology Numeristan HOTzone Astrostan Infostan Interpretive Biology Integrative Biology Computational Biology Bioinformatics 11/25/2002 ©Bud Mishra, 2002 Bio. Spice Cell Talk» 3

Computational/Systems Biology How much of reasoning about biology can be automated? 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 4

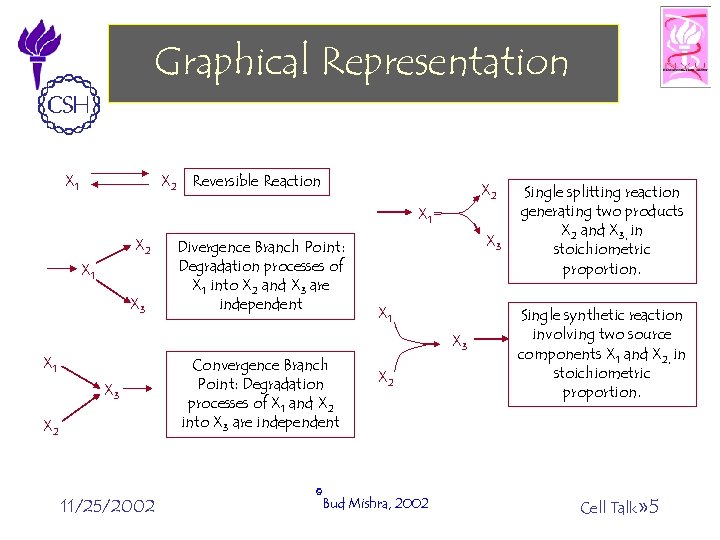Graphical Representation X 2 Reversible Reaction X 1 X 2 X 1 X 3 Divergence Branch Point: Degradation processes of X 1 into X 2 and X 3 are independent X 3 X 1 X 3 X 2 11/25/2002 Convergence Branch Point: Degradation processes of X 1 and X 2 into X 3 are independent X 2 ©Bud Mishra, 2002 Single splitting reaction generating two products X 2 and X 3, in stoichiometric proportion. Single synthetic reaction involving two source components X 1 and X 2, in stoichiometric proportion. Cell Talk» 5

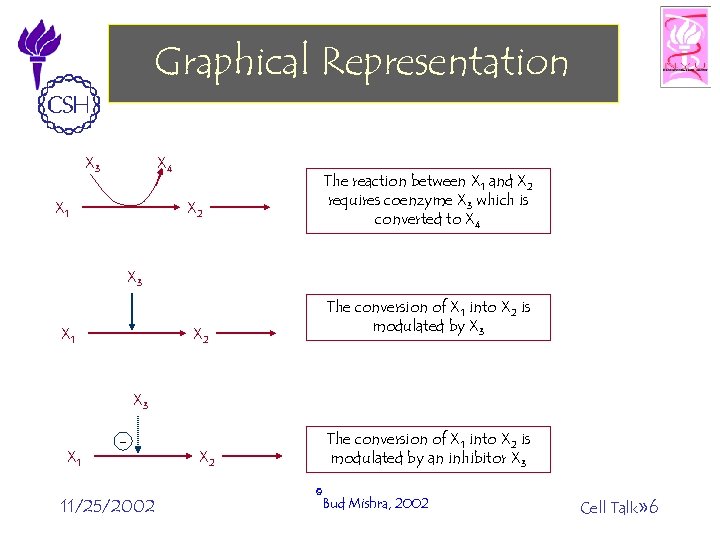Graphical Representation X 3 X 4 X 2 X 1 The reaction between X 1 and X 2 requires coenzyme X 3 which is converted to X 4 X 3 X 2 X 1 The conversion of X 1 into X 2 is modulated by X 3 X 1 - 11/25/2002 X 2 The conversion of X 1 into X 2 is modulated by an inhibitor X 3 ©Bud Mishra, 2002 Cell Talk» 6

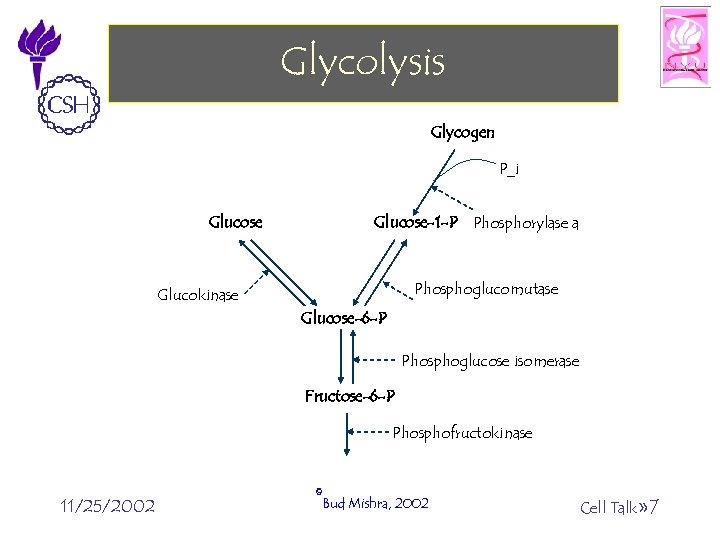Glycolysis Glycogen P_i Glucose-1 -P Phosphorylase a Phosphoglucomutase Glucokinase Glucose-6 -P Phosphoglucose isomerase Fructose-6 -P Phosphofructokinase 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 7

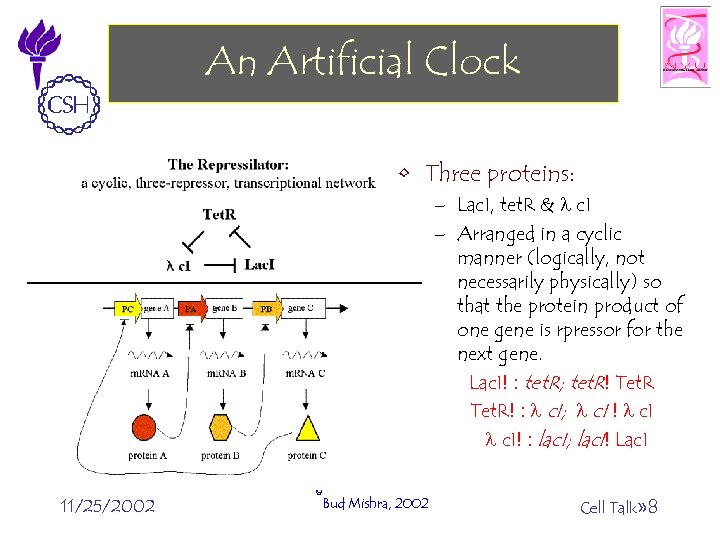An Artificial Clock • Three proteins: – Lac. I, tet. R & l c. I – Arranged in a cyclic manner (logically, not necessarily physically) so that the protein product of one gene is rpressor for the next gene. Lac. I! : tet. R; tet. R! Tet. R! : l c. I; l c. I ! l c. I! : lac. I; lac. I! Lac. I 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 8

Cycles of Repression • The first repressor protein, Lac. I from E. coli inhibits the transcription of the second repressor gene, tet. R from the tetracycline-resistance transposon Tn 10. • Protein product in turn Tet. R from tet. R inhibits the expression of a third gene, c. I from l phage. • Finally, CI inhibits lac. I expression, completing the cycle. 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 9

Biological Model • Standard molecular biology: Construct – A low-copy plasmid encoding the repressilator and – A compatible higher-copy reporter plasmid containing the tet-repressible promoter PLtet 01 fused to an intermediate stability variant of gfp. 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 10

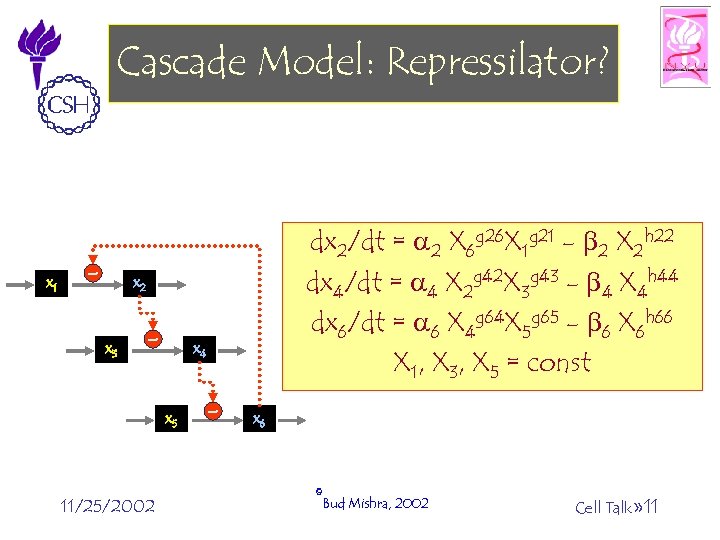Cascade Model: Repressilator? x 1 - dx 2/dt = a 2 X 6 g 26 X 1 g 21 - b 2 X 2 h 22 dx 4/dt = a 4 X 2 g 42 X 3 g 43 - b 4 X 4 h 44 dx 6/dt = a 6 X 4 g 64 X 5 g 65 - b 6 X 6 h 66 X 1, X 3, X 5 = const x 2 x 3 - x 4 x 5 11/25/2002 - x 6 ©Bud Mishra, 2002 Cell Talk» 11

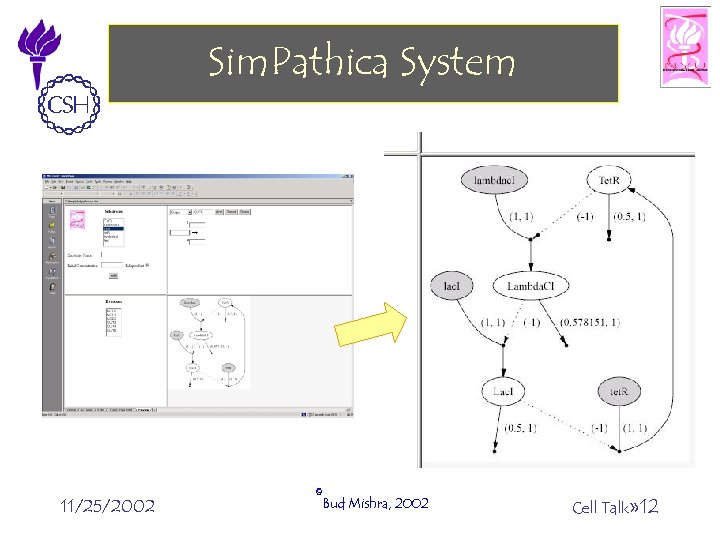Sim. Pathica System 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 12

Modal Logic Queries 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 13

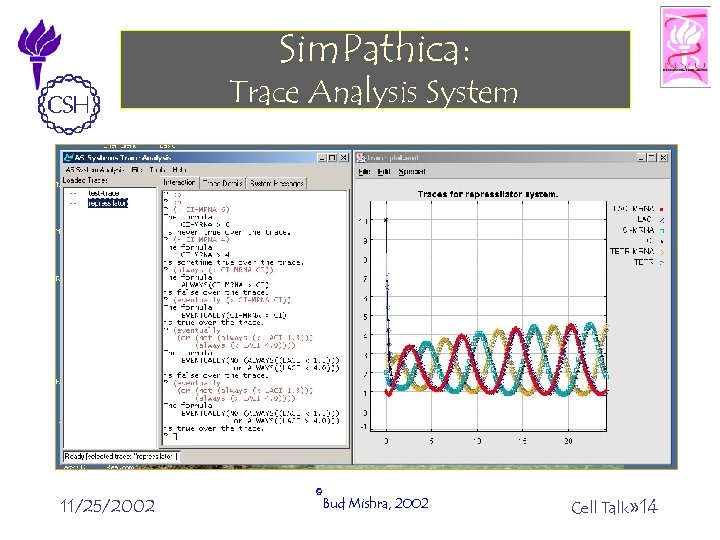Sim. Pathica: Trace Analysis System 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 14

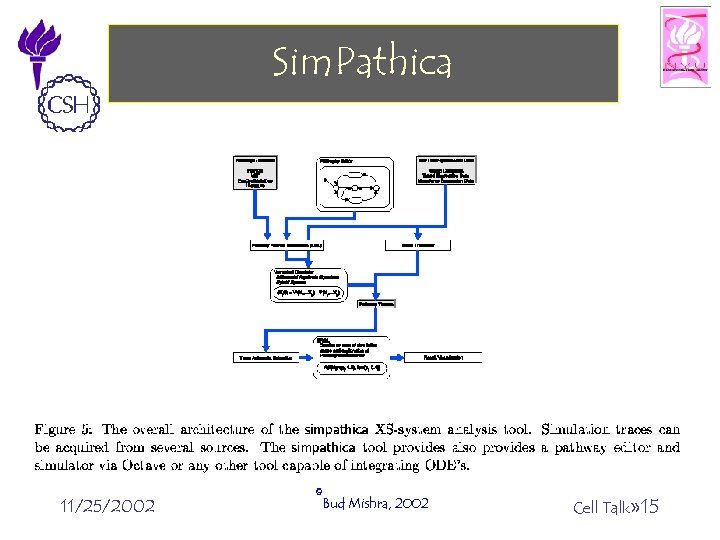Sim. Pathica 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 15

Canonical Forms 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 16

Systems of Differential Equations • d. Xi/dt = (instantaneous) rate of change in Xi at time t = Function of substrate concentrations, enzymes, factors and products: d. Xi/dt = f(S 1, S 2, …, E 1, E 2, …, F 1, F 2, …, P 1, P 2, …) • S-systems result in Non-linear Time-Invariant DAE System. 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 17

General Form • d. Xi/dt = Vi+(X 1, X 2, …, Xn) – Vi-(X 1, X 2, …, Xn): – Where Vi+(¢) term represents production (or accumulation) rate of a particular metabolite and Vi-(¢) represent s depletion rate of the same metabolite. • Generalizing to n dependent variables and m independent variables, we have: d. Xi/dt = Vi+(X 1, X 2, …, Xn, U 1, U 2, …, Um) – Vi-(X 1, X 2, …, Xn, U 1, U 2, …, Um): 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 18

Canonical Forms 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 19

S-System Automaton AS • S-System Automata Definition: – Combine snapshots of the IDs (“instantaneous descriptions”) of the system to create a possible world model – Transitions are inferred from “traces” of the system variables: • Definition: Given an S-systems S, the S-system automaton AS associated to S is 4 -tuple AS = (S, D, S 0, F), where S µ D 1 £ L £ DW is a set of states, D µ S £ S is the binary transition relation, and S 0, F ½ S are initial and final states respectively. • Definition: A trace of an S-system automaton AS is a sequence s 0, s 1, …, sn, …, such that s 0 2 S 0, D(si, si+1), 8 i = 0. 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 20

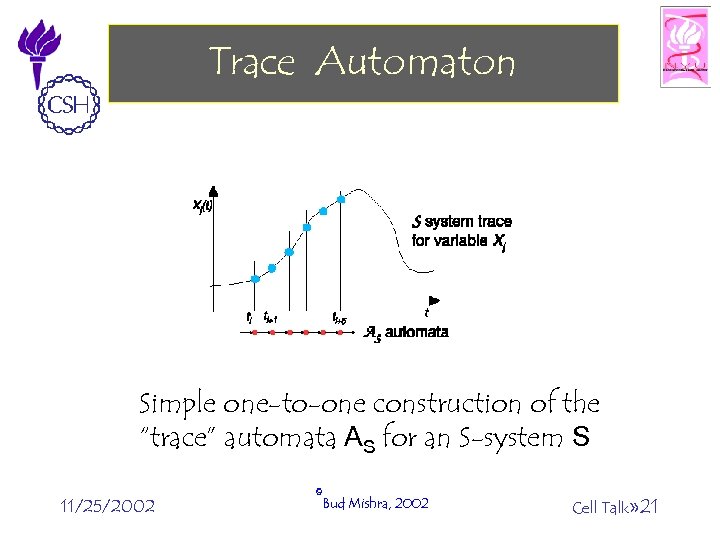Trace Automaton Simple one-to-one construction of the “trace” automata AS for an S-system S 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 21

Collapsing Algorithm 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 22

Collapsed Automata The effects of the collapsing construction of the “trace” automata AS for an S-system S 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 23

Purine Metabolism 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 24

Purine Metabolism • Purine Metabolism – Provides the organism with building blocks for the synthesis of DNA and RNA. – The consequences of a malfunctioning purine metabolism pathway are severe and can lead to death. • The entire pathway is almost closed but also quite complex. It contains – several feedback loops, – cross-activations and – reversible reactions • Thus is an ideal candidate for reasoning with computational tools. 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 25

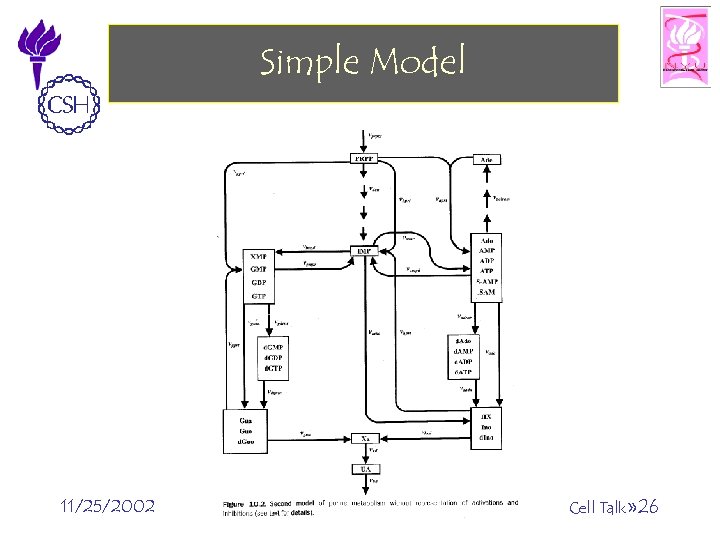Simple Model 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 26

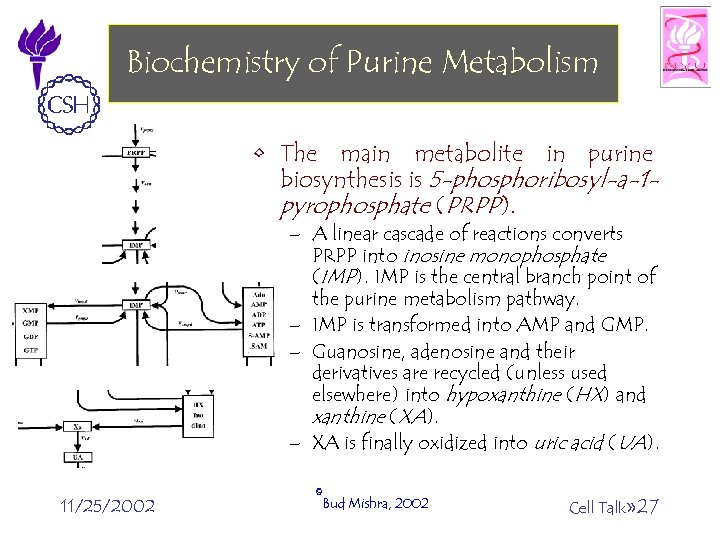Biochemistry of Purine Metabolism • The main metabolite in purine biosynthesis is 5 -phosphoribosyl-a-1 pyrophosphate (PRPP). – A linear cascade of reactions converts PRPP into inosine monophosphate (IMP). IMP is the central branch point of the purine metabolism pathway. – IMP is transformed into AMP and GMP. – Guanosine, adenosine and their derivatives are recycled (unless used elsewhere) into hypoxanthine (HX) and xanthine (XA). – XA is finally oxidized into uric acid (UA). 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 27

Biochemistry of Purine Metabolism • In addition to these processes, there appear to be two “salvage” pathways that serve to maintain IMP level and thus of adenosine and guanosine levels as well. • In these pathways, adenine phosphoribosyltransferase (APRT) and hypoxanthine-guanine phosphoribosyltransferase (HGPRT) combine with PRPP to form ribonucleotides. 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 28

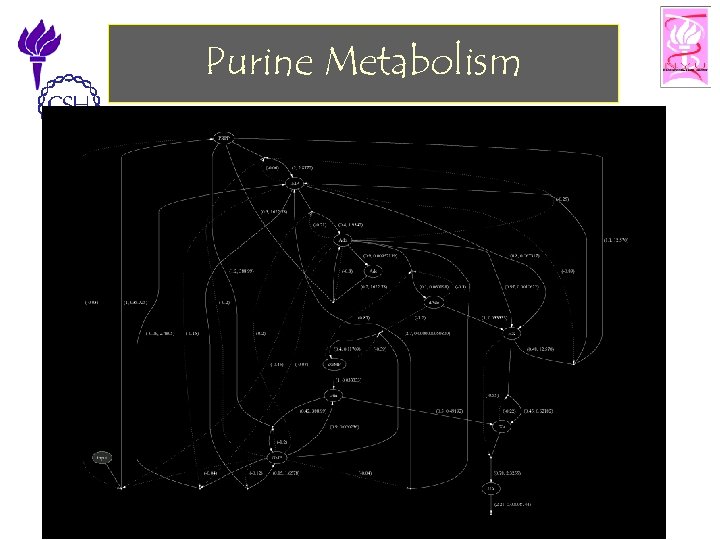Purine Metabolism 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 29

-

Queries • Variation of the initial concentration of PRPP does not change the steady state. (PRPP = 10 * PRPP 1) implies steady_state() This query will be true when evaluated against the modified simulation run (i. e. the one where the initial concentration of PRPP is 10 times the initial concentration in the first run – PRPP 1). • Persistent increase in the initial concentration of PRPP does cause unwanted changes in the steady state values of some metabolites. • If the increase in the level of PRPP is in the order of 70% then the system does reach a steady state, and we expect to see increases in the levels of IMP and of the hypoxanthine pool in a “comparable” order of magnitude. TRUE Always (PRPP = 1. 7*PRPP 1) implies steady_state() • 11/25/2002 ©Bud Mishra, 2002 TRUE Cell Talk» 31

Queries • Consider the following statement: Eventually (Always (PRPP = 1. 7 * PRPP 1) implies steady_state() and Eventually (Always(IMP < 2 * IMP 1)) and Eventually (Always (hx_pool < 10*hx_pool 1))) where IMP 1 and hx_pool 1 are the values observed in the unmodified trace. The above statement turns out to be false over the modified experiment trace. . False 11/25/2002 ©Bud Mishra, 2002 • In fact, the increase in IMP is about 6. 5 fold while the hypoxanthine pool increase is about 60 fold. • Since the above queries turn out to be false over the modified trace, we conclude that the model “over-predicts” the increases in some of its products and that it should therefore be amended Cell Talk» 32

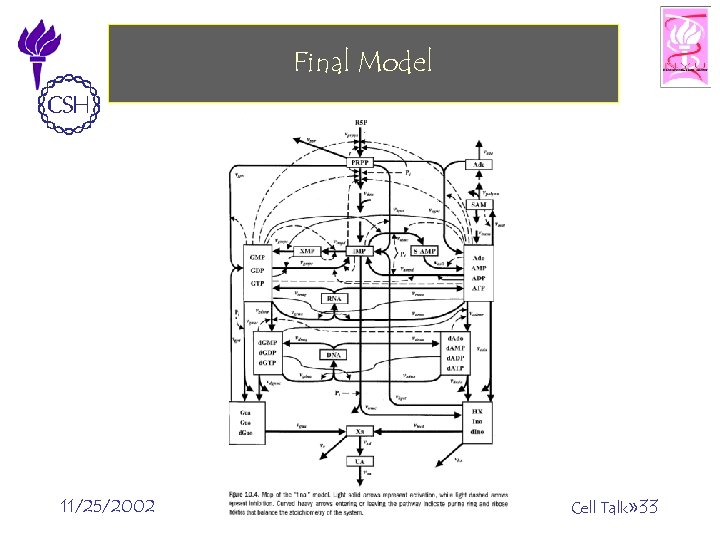Final Model 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 33

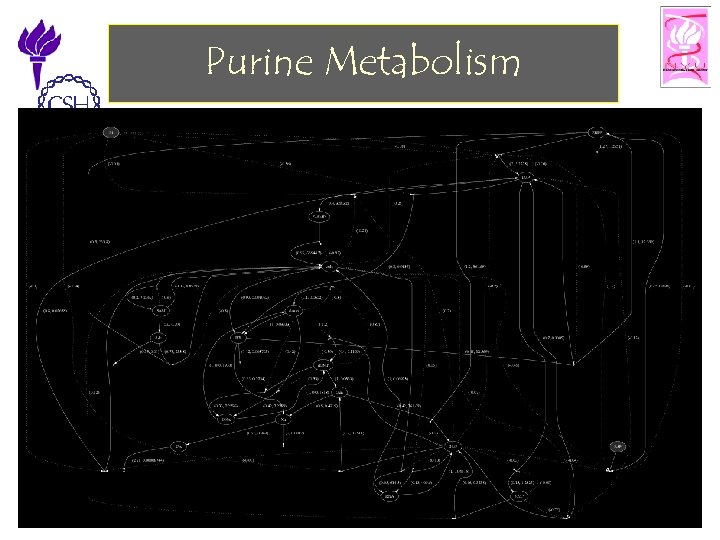Purine Metabolism 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 34

Query • This change to the model allows us to reformulate our query as shown below: Always(PRPP > 50 * PRPP 1 implies (steady_state() and Eventually(IMP > IMP 1) and Eventually(HX < HX 1) and Eventually(Always(IMP = IMP 1)) and Eventually(Always(HX = HX 1)) • An (instantaneous) increase in the level of PRPP will not make the system stray from the predicted steady state, even if temporary variations of IMP and HX are allowed. TRUE 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 36

Related Publications • “Simulating Large Biochemical and Biological Processes and Reasoning about their Behavior. " (with M. Antoniotti, F. Park, A. Policriti and N. Ugel), ICSB, Sweden, 2003. • "Foundations of a Query and Simulation System for the Modeling of Biochemical and Biological Processes. " (with M. Antoniotti, F. Park, A. Policriti and N. Ugel), The Pacific Symposium on Biocomputing (PSB 2003), Hawaii, January 3 -7, 2003. • "Model Building and Model Checking for Biochemical Processes , " (with M. Antoniotti, A. Policriti and N. Ugel), Cell Biochemistry and Biophysics (CBB), Humana Press, 2003, (In press) • "A Symbolic Approach to Modelling Cellular Behaviour, " International Conference On High Performance Computing, Hi. PC 2002, December 1821, Bangalore, India, 2002. (In Press) • "Wild by Nature, " (with M. Wigler), Science, 296: 1407 -1408, 24 May 2002. 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 48

The End Websites http: //cs. nyu. edu/faculty/mishra/ http: //bioinformatics. cat. nyu. edu/ 11/25/2002 ©Bud Mishra, 2002 Cell Talk» 49