Hedging and Value-at-Risk Va R Single asset Va

Hedging and Value-at-Risk (Va. R) Single asset Va. R Delta-Va. R for portfolios Delta-Gamma Va. R simulated Va. R Finance 70520, Spring 2002 Risk Management & Financial Engineering S. Mann The Neeley School

Value at Risk (Va. R) “Va. R measures the worst expected loss over a given time interval under normal market conditions at a given confidence level. ” - Jorion (1997) “Value at Risk is an estimate, with a given degree of confidence, of how much one can lose from one’s portfolio over a given time horizon. ” - Wilmott (1998) “Value-at-Risk or VAR is a dollar measure of the minimum loss that would be expected over a period of time with a given probability” - Chance(1998) 95% confidence level Va. R 5% probability minimum loss (over given horizon) max. loss with 95% confidence min. loss with 5% probability (for given time interval)

Asset price standard deviation Assume lognormal returns: Let d. S/S ~ lognormal(m, s) where s is annualized return volatility (standard deviation) The standard deviation of the asset price (S) over a period t is: S (s t. 5) = S ( s t ) For example, let S = $ 100. 00 s = 40% t = 1 week = 1/52 then the weekly standard deviation (s. d. ) of the price is weekly s. d. = 100 (0. 40) (. 192). 5 = 40(0. 139) = $ 5. 55 similarly, daily s. d. = 100(0. 40)(1/252). 5 = 40(0. 063) = $ 2. 52 monthly s. d. = 0. 40(0. 40)(1/12). 5 = 40(0. 289) = $ 11. 55

Confidence levels and the inverse distribution function Let Va. R = - S (s t) N`(1 - confidence level) (for long position in underlying asset) where N`(x%) = inverse cumulative distribution function for the standard normal N`(x%) = number of standard deviations from the mean such that the probability of obtaining a lower outcome is x% example: desired confidence level is 95%, then N`(1 -. 95) = N`(5%) = - 1. 65 In other words, N(-1. 65) = 0. 05 (5%) so N`(0. 05) = -1. 65 Standard normal distribution -1. 65 -1 0 1 1. 65 5% probability of return lower than 1. 65 standard deviations below the mean

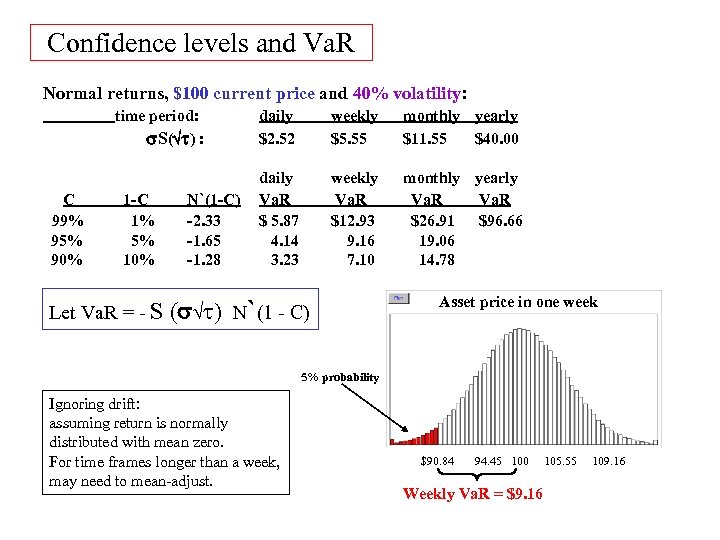Confidence levels and Va. R Normal returns, $100 current price and 40% volatility: time period: s. S( t) : C 99% 95% 90% 1 -C 1% 5% 10% Let Va. R = - S N`(1 -C) -2. 33 -1. 65 -1. 28 daily $2. 52 weekly $5. 55 monthly yearly $11. 55 $40. 00 daily Va. R $ 5. 87 4. 14 3. 23 weekly Va. R $12. 93 9. 16 7. 10 monthly yearly Va. R $26. 91 $96. 66 19. 06 14. 78 (s t) N`(1 - C) Asset price in one week 5% probability Ignoring drift: assuming return is normally distributed with mean zero. For time frames longer than a week, may need to mean-adjust. $90. 84 94. 45 100 Weekly Va. R = $9. 16 105. 55 109. 16

Call greeks delta (D) = C/ S = call sensitivity to asset value vba function: delta(S, K, T, r, s) gamma (G) = 2 C/ S 2 = delta sensitivity to asset value vba function: gamma(S, K, T, r, s) vega = C/ s = call sensitivity to volatility vba function: vega(S, K, T, r, s) theta = C/ T = call sensitivity to time vba function: calltheta(S, K, T, r, s) rho = C/ r = call sensitivity to riskless rate vba function: callrho(S, K, T, r, s)

Put Delta and Gamma Put-Call parity: S + P = C + KB(0, T) take derivative of equality with respect to asset price, S. S/ S + P/ S = C/ S + [KB(0, T)]/ S 1 + P/ S = C/ S + 0 P/ S = C/ S - 1 Put Delta: Dp = Dc - 1 (put delta = call delta - 1) Take second derivative with respect to asset price, S. [ P/ S]/ S = [ C/ S]/ S + (1)/ S 2 P/ S 2 Put Gamma: Gp = = 2 C/ S 2 + Gc (put gamma = call gamma) 0

Put vega and theta Put-Call parity: S + P = C + KB(0, T) take derivative of equality with respect to volatility, s. S/ s + P/ s = C/ s + [KB(0, T)]/ s 0 + P/ s = C/ s + 0 P/ s = C/ s Put Vega = Call Vega take derivative of equality with respect to time, T. S/ T + P/ T = C/ T + [KB(0, T)]/ T + P/ T = C/ T + K( B(0, T)/ T) P/ T 0 = C/ T + K (e Put theta = Call theta + r. K e -r. T Call theta is always negative; put theta is ambiguous -r. T )/ T

Put greeks delta (D) = P/ S = put sensitivity to asset value put delta = call delta -1 Dp = Dc - 1 ; function: delta(S, K, T, r, s) - 1 gamma (G) = 2 P/ S 2 = delta sensitivity to asset value put gamma = call gamma function: gamma(S, K, T, r, s) vega theta = P/ s = put sensitivity to volatility put vega = call vega function: vega(S, K, T, r, s) = P/ T = put sensitivity to time vba function: puttheta(S, K, T, r, s) rho = P/ r = put sensitivity to riskless rate vba function: putrho(S, K, T, r, s)

Call Va. R: Delta-Va. R for long position in underlying asset: VAR = -s. S( t ) N`(1 -C) Since D represents call exposure to underlying, (for small moves, if asset increases $1, call increases $D) define e. g. Delta-Va. R = -s. DS( t ) N`(1 -C), = DVa. R example: $100 stock, 40% volatility, 95% daily VAR = $4. 14 Examine 95% daily D-Va. R for the following 110 -day calls: Strike Value D 95% D-Va. R (D-Va. R)/Cost 95 100 105 110 11. 96 9. 36 7. 21 5. 47 0. 66 0. 57 0. 48 0. 40 2. 72 2. 35 1. 99 1. 64 22. 8% 25. 1% 27. 6% 30. 0%

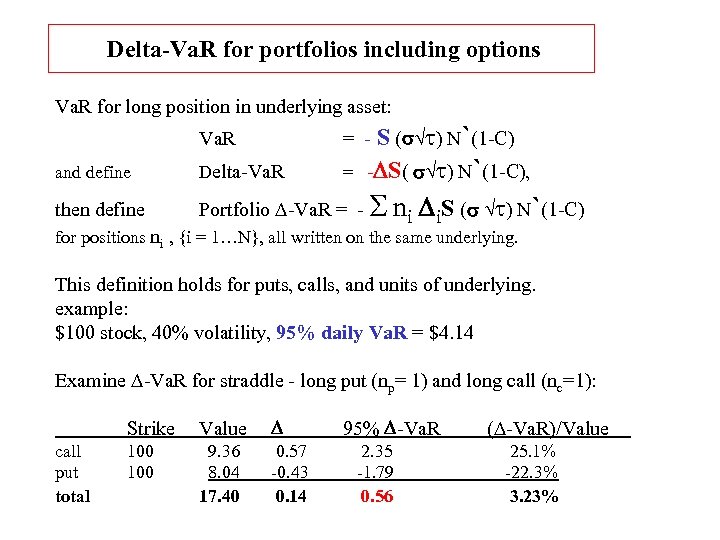Delta-Va. R for portfolios including options Va. R for long position in underlying asset: S (s t) N`(1 -C) -DS( s t) N`(1 -C), Va. R = - and define Delta-Va. R = then define Portfolio D-Va. R = - S ni Di. S (s t) N`(1 -C) for positions ni , {i = 1…N}, all written on the same underlying. This definition holds for puts, calls, and units of underlying. example: $100 stock, 40% volatility, 95% daily Va. R = $4. 14 Examine D-Va. R for straddle - long put (np= 1) and long call (nc=1): Strike call put total Value D 100 9. 36 8. 04 17. 40 0. 57 -0. 43 0. 14 95% D-Va. R 2. 35 -1. 79 0. 56 (D-Va. R)/Value 25. 1% -22. 3% 3. 23%

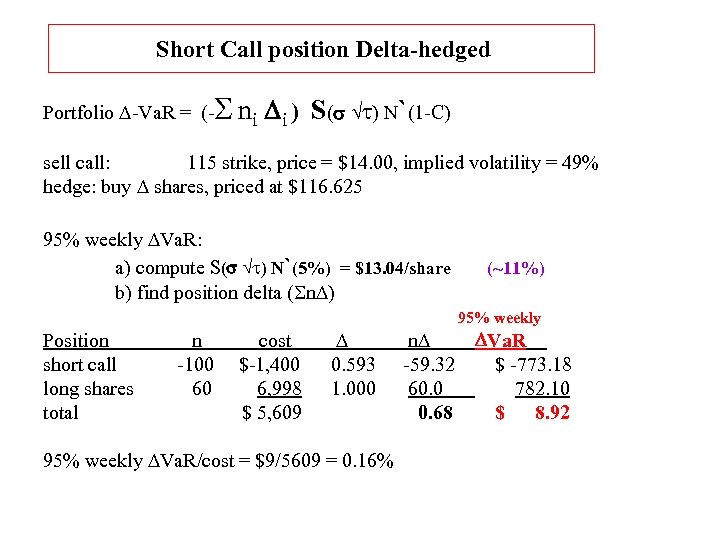Short Call position Delta-hedged Portfolio D-Va. R = (- S ni Di ) S(s t) N`(1 -C) sell call: 115 strike, price = $14. 00, implied volatility = 49% hedge: buy D shares, priced at $116. 625 95% weekly DVa. R: a) compute S(s t) N`(5%) = $13. 04/share b) find position delta (Sn. D) (~11%) 95% weekly Position short call long shares total n -100 60 cost $-1, 400 6, 998 $ 5, 609 D 0. 593 1. 000 95% weekly DVa. R/cost = $9/5609 = 0. 16% n. D -59. 32 60. 0 0. 68 DVa. R $ -773. 18 782. 10 $ 8. 92

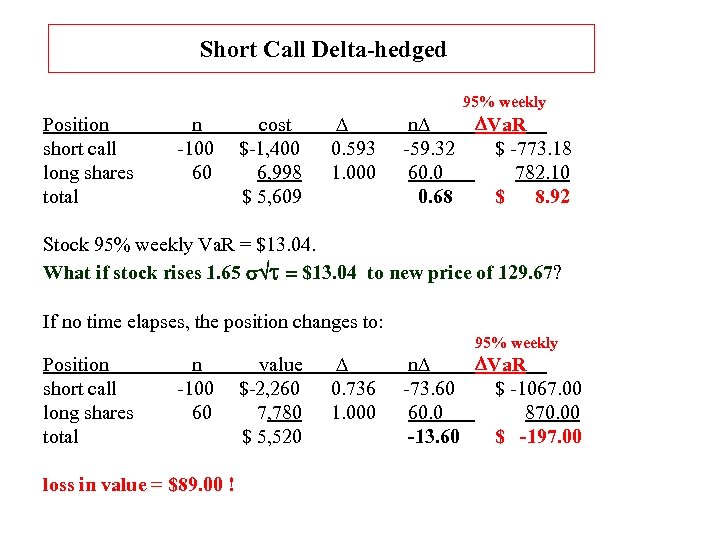Short Call Delta-hedged 95% weekly Position short call long shares total n -100 60 cost $-1, 400 6, 998 $ 5, 609 D 0. 593 1. 000 n. D -59. 32 60. 0 0. 68 DVa. R $ -773. 18 782. 10 $ 8. 92 Stock 95% weekly Va. R = $13. 04. What if stock rises 1. 65 s t = $13. 04 to new price of 129. 67? If no time elapses, the position changes to: Position short call long shares total n -100 60 loss in value = $89. 00 ! value $-2, 260 7, 780 $ 5, 520 D 0. 736 1. 000 95% weekly n. D DVa. R -73. 60 $ -1067. 00 60. 0 870. 00 -13. 60 $ -197. 00

Adjusting D-Va. R for nonlinearity Use Taylor-series expansion of function: given value at x 0, use derivatives of function to approximate value of function at x: f(x) = f(x 0) + f ' (x 0) (x-x 0) + (1/2) f '' (x 0)(x-x 0)2 +. . . Incorporate curvature via Second-order Taylor series expansion of option price around the stock price (quadratic approximation): C(S + d. S) = C(S) + ( C/ S) d. S + (0. 5) 2 C/ S 2 (d. S)2 = C(S) + D d. S + 0. 5 G (d. S)2 so that C(S + d. S) - C(S) = D d. S + 0. 5 G (d. S)2 + … or d. C = D d. S + 0. 5 G (d. S)2 + …

quadratic approximation of call price variance we want an expression for the standard deviation of an option’s price Quadratic approximation of change in call value for given change in stock value: d. C = D d. S + 0. 5 G (d. S)2 + … then the variance of the call’s price, V(d. C) for given time, t , is: V(d. C) = D 2 V(d. S) + 0. 5 [ G V(d. S) ]2 note that V(d. S) = S 2 s 2 t = variance of stock price over period t so that thus V(d. C) = D 2 S 2 s 2 t + 0. 5 [ G S 2 s 2 t ]2 the standard deviation of the option price is: s. d. (d. C) = (what if G = 0? ) { D S s t + 0. 5 [ G S s t ] }(1/2) 2 2 2 if G = 0 then s. d. (d. C) = DSs t 2 2 2

Delta-Gamma Va. R Taylor expansion leads to quadratic approximation for the standard deviation of the option price: s. d. (d. C) = { D 2 S 2 s 2 t + 0. 5 [ G S 2 s 2 t ]2 } (1/2) Note that if G = 0 then s. d. (d. C) = DSs t Examine Delta-Va. R: D-Va. R = D Ss t N (1 -C) delta-Va. R is a linear operator on underlying asset Va. R Delta-Gamma Va. R = option s. d. N (1 -C) (1/2) = [D 2 S 2 s 2 t + 0. 5 [ G S 2 s 2 t ]2] N (1 -C) delta-Gamma Va. R is nonlinear function of asset Va. R

Calculating portfolio Delta-Gamma Va. R = option s. d. N (1 -C) 2 S 2 s 2 t + 0. 5 [ G S 2 s 2 t ]2](1/2) N (1 -C) = [D Since Delta-Gamma Va. R is nonlinear function of Delta and Gamma, cannot simply add Va. R, as in Delta-Va. R. For portfolio of linear and/or nonlinear derivatives on a single underlying: Solution: 1) compute portfolio Delta Dp 2) compute portfolio Gamma Gp 3) compute the quadratic approximation to the portfolio standard deviation [Dp 2 S 2 s 2 t + 0. 5 (Gp S 2 s 2 t)2] (1/2) 4) multiply the portfolio standard deviation by N (1 -C) to get D-G Va. R

Delta-Gamma Va. R for delta-hedged short call Position short call long shares total n -100 60 cost $-1, 400 6, 998 $ 5, 609 D 0. 593 1. 0 n. D -59. 32 60. 0 0. 68 G 0. 012 0 n. G -1. 2 0 -1. 2 Find quadratic approximation to position standard deviation: (1/2) 2 S 2 s 2 t + 0. 5 (G S 2 s 2 t)2] [D p =[ (0. 68)2(62. 80) +. 5 (-1. 2 x 62. 80)2 ] (1/2) p =[ 0. 4679 (62. 80) +. 5 (-78. 03)2 ] (1/2) =[ 29. 3875 +. 5 ( 6088. 81) ] (1/2) =[ 29. 3875 + 3044. 40 ](1/2) =[ 3073. 79 ] (1/2) = 55. 44 (using S = 116. 625, s = 49%, t = 1 week, so that Ss t = $7. 92; S 2 s 2 t = $62. 80) Multiply the portfolio standard deviation by N (1 -C) = -1. 65 for C=95% Delta-Gamma Va. R = 55. 44 x (-1. 65) = -91. 19

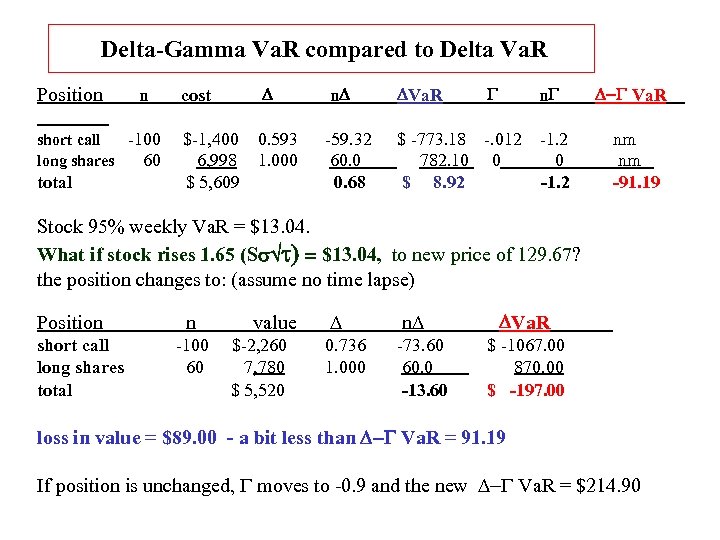Delta-Gamma Va. R compared to Delta Va. R Position n short call -100 long shares 60 total cost D n. D DVa. R G $-1, 400 6, 998 $ 5, 609 0. 593 1. 000 -59. 32 60. 0 0. 68 $ -773. 18 -. 012 782. 10 0 $ 8. 92 n. G -1. 2 0 -1. 2 D-G Va. R nm nm -91. 19 Stock 95% weekly Va. R = $13. 04. What if stock rises 1. 65 (Ss t) = $13. 04, to new price of 129. 67? the position changes to: (assume no time lapse) Position short call long shares total n -100 60 value $-2, 260 7, 780 $ 5, 520 D n. D 0. 736 1. 000 -73. 60 60. 0 -13. 60 DVa. R $ -1067. 00 870. 00 $ -197. 00 loss in value = $89. 00 - a bit less than D-G Va. R = 91. 19 If position is unchanged, G moves to -0. 9 and the new D-G Va. R = $214. 90

Alternative Va. R approaches - Monte Carlo simulate distributions of underlying assets; for each simulated outcome use pricing model to evaluate portfolio (underlying and options). Heavy computational requirements. Requires many inputs (e. g. variance, correlations) Assumes specific return-generating process (e. g. normal). Should use expected returns (not risk-neutral drift, as in monte carlo pricing).

Alternative Va. R approaches - Bootstrapping (historical) database of return vectors (e. g. , rt = r 1 t, r 2 t, …. r. Nt ) randomly sample from historical returns to generate return sequences - potential future scenarios based on historical data. All asset returns on given date are kept together - thus the bootstrap captures historical correlations between assets. Incorporates correlation, but not autocorrelation. Allows for non-normality. Data requirements are large.

references Chance, Don, 1998. An Introduction to Derivatives. The Dryden Press. Jorion, Phillipe, 1997. Value at Risk: The New Benchmark for controlling market risk. Irwin Professional Publishing. Stulz, Rene, 1999. Derivatives, Financial Engineering, and Risk Management. South-Western College Publishing (in press). Wilmott, Paul, 1998. Derivatives - Theory and Practice of Financial Engineering. John Wiley & Sons. (www. wilmott. com)