Heavy Atom Quantum Diffraction by Scattering from Surfaces Eli Pollak Chemical Physics Department Weizmann Institute of Science Coworkers: Dr. Jeremy M. Moix Grants: Israel Science Foundation Weizmann-UK Joint Research Program
http: //www. ams. org/featurecolumn/archive/rainbows. html Bill Casselman University of British Columbia, Vancouver, Canada cass at math. ubc. ca
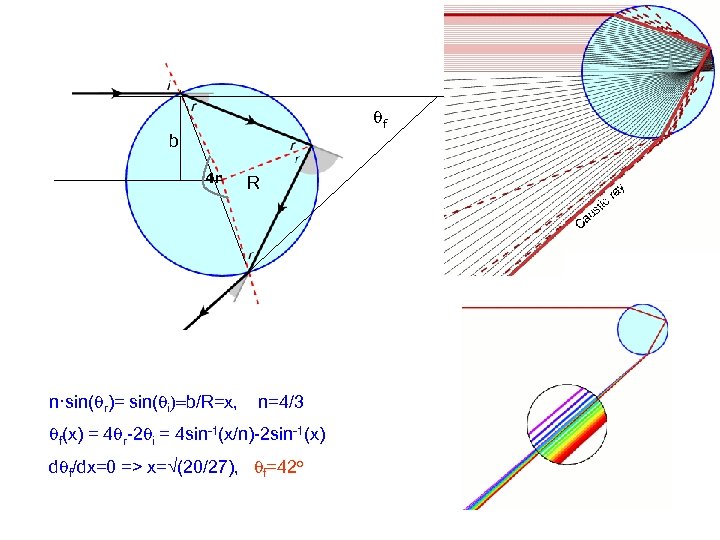
qf b 4 r R n·sin(qr)= sin(qi)=b/R=x, n=4/3 qf(x) = 4 qr-2 qi = 4 sin-1(x/n)-2 sin-1(x) dqf/dx=0 => x=√(20/27), qf=42 o
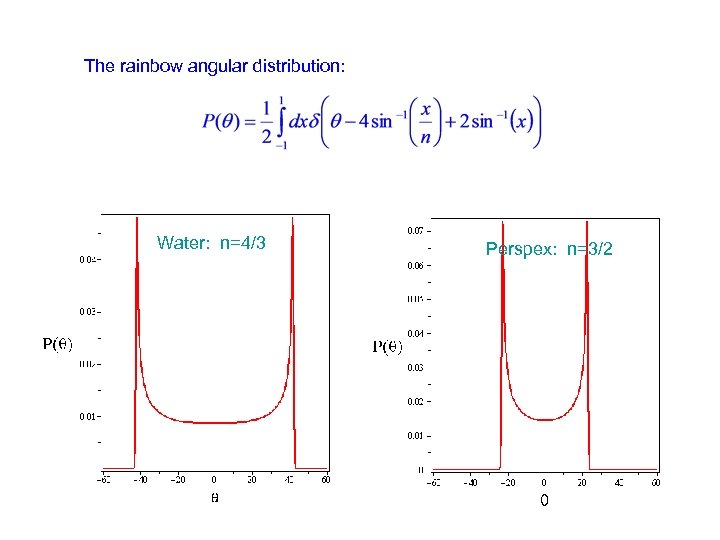
The rainbow angular distribution: Water: n=4/3 Perspex: n=3/2
![Rainbow scattering from a hard wall h(x) p/2 -f-qi f f=-tan-1[h’(x)]~-h’(x) qf (x)=qi+2 f~qi-2](https://present5.com/presentation/5a4b1362eeca010cdd8dbf9f9d9a588b/image-5.jpg "Rainbow scattering from a hard wall h(x) p/2 -f-qi f f=-tan-1[h’(x)]~-h’(x) qf (x)=qi+2 f~qi-2")
Rainbow scattering from a hard wall h(x) p/2 -f-qi f f=-tan-1[h’(x)]~-h’(x) qf (x)=qi+2 f~qi-2 h’(x) qi p/2 -f qf p/2 -f-qi x l The rainbow angles are found when they arise from the deflection points of the corrugation function.
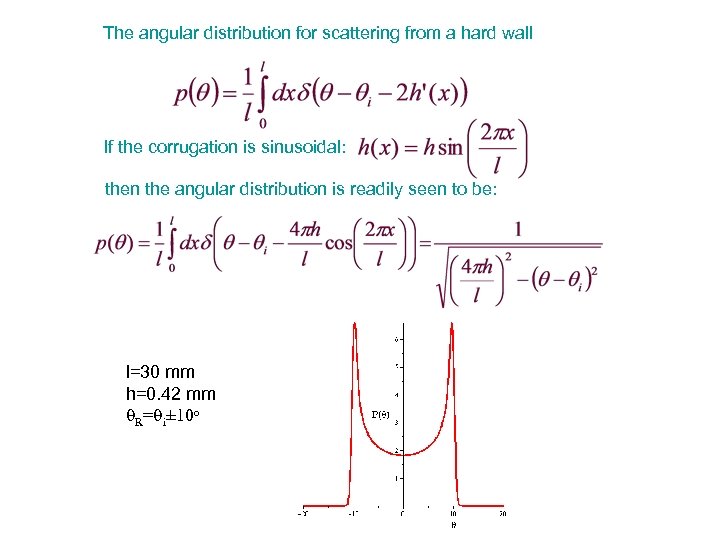
The angular distribution for scattering from a hard wall If the corrugation is sinusoidal: then the angular distribution is readily seen to be: l=30 mm h=0. 42 mm q. R=qi± 10 o
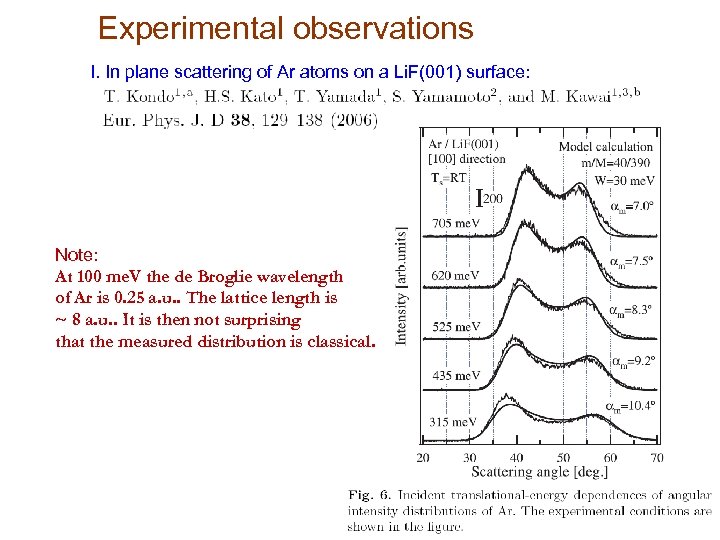
Experimental observations I. In plane scattering of Ar atoms on a Li. F(001) surface: Note: At 100 me. V the de Broglie wavelength of Ar is 0. 25 a. u. . The lattice length is ~ 8 a. u. . It is then not surprising that the measured distribution is classical.
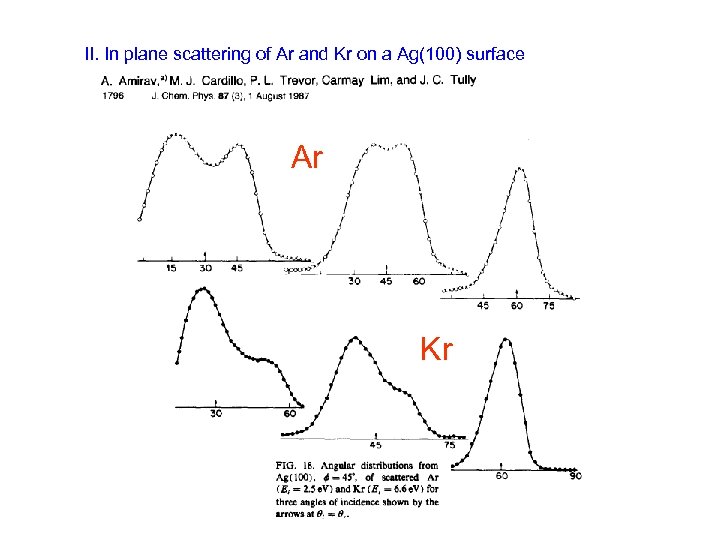
II. In plane scattering of Ar and Kr on a Ag(100) surface Ar Kr
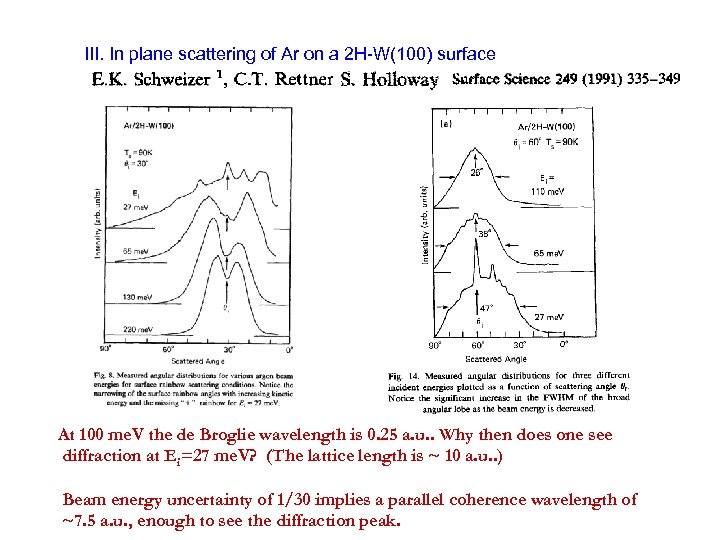
III. In plane scattering of Ar on a 2 H-W(100) surface At 100 me. V the de Broglie wavelength is 0. 25 a. u. . Why then does one see diffraction at Ei=27 me. V? (The lattice length is ~ 10 a. u. . ) Beam energy uncertainty of 1/30 implies a parallel coherence wavelength of ~7. 5 a. u. , enough to see the diffraction peak.
Krypton mass - ~84, at 35 me. V, d. Bwl~0. 3 a. u. . Beam energy uncertainty of 1/35 implies a parallel coherence wavelength of ~10 a. u. , enough to see the diffraction peak.
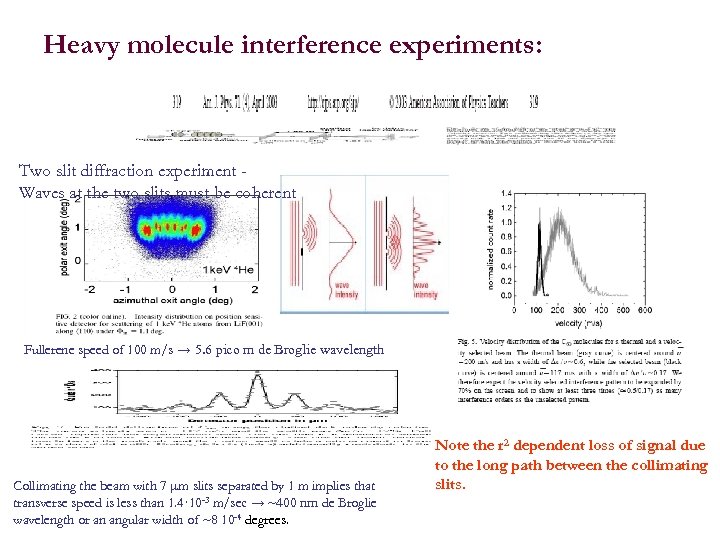
Heavy molecule interference experiments: Two slit diffraction experiment Waves at the two slits must be coherent Fullerene speed of 100 m/s → 5. 6 pico m de Broglie wavelength Collimating the beam with 7 mm slits separated by 1 m implies that transverse speed is less than 1. 4· 10 -3 m/sec → ~400 nm de Broglie wavelength or an angular width of ~8 10 -4 degrees. Note the r 2 dependent loss of signal due to the long path between the collimating slits.
High energy grazing collisions Diffraction of Fast Atomic Projectiles during Grazing Scattering from a Li. F(001) Surface PRL 98, 016103 (2007) A. Schueller, S. Wethekam, and H. Winter* Institut fuer Physik, Humboldt Universita¨t zu Berlin, Brook-Taylor-Strasse 6, D-12489 Berlin. Adlershof, Germany Light atoms and molecules with energies from 300 e. V to 25 ke. V are scattered under a grazing angle of incidence from a Li. F(001) surface…. Experimental results for scattering of H, D, 3 He, and 4 He atoms as well as H 2 and D 2 molecules can be unequivocally referred to atom diffraction with de Broglie wavelengths as low as about 0. 001 A° Analysis: At 10 ke. V the de Broglie wavelength of 4 He is 0. 0027 a. u. a 1 o grazing angle implies p┴~p║/60 so a perpendicular wavelength of 0. 16 a. u. . The angular resolution is ~0. 01 o so that the coherence wavelength is ~16 a. u. , enough to observe diffraction.
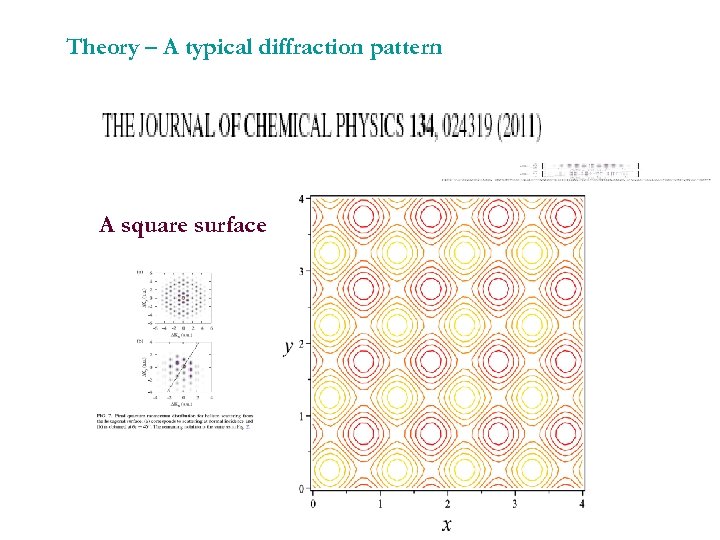
Theory – A typical diffraction pattern A square surface
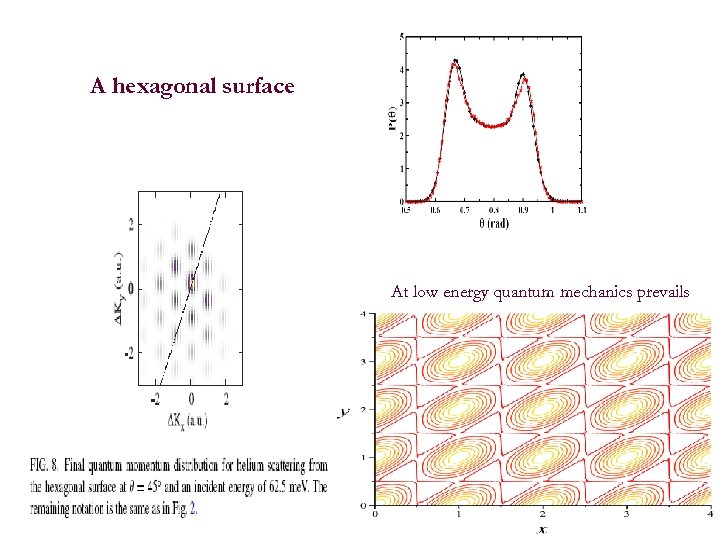
A hexagonal surface At low energy quantum mechanics prevails
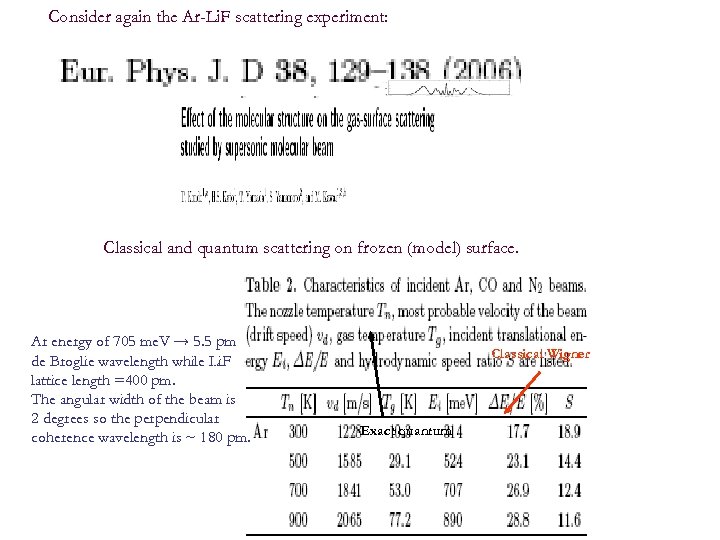
Consider again the Ar-Li. F scattering experiment: Classical and quantum scattering on frozen (model) surface. Ar energy of 705 me. V → 5. 5 pm de Broglie wavelength while Li. F lattice length =400 pm. The angular width of the beam is 2 degrees so the perpendicular coherence wavelength is ~ 180 pm. Classical Wigner Exact quantum
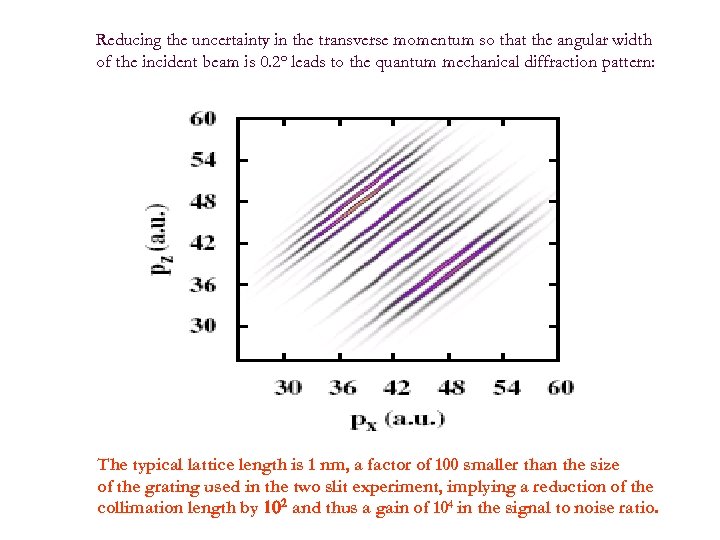
Reducing the uncertainty in the transverse momentum so that the angular width of the incident beam is 0. 2 o leads to the quantum mechanical diffraction pattern: The typical lattice length is 1 nm, a factor of 100 smaller than the size of the grating used in the two slit experiment, implying a reduction of the collimation length by 102 and thus a gain of 104 in the signal to noise ratio.
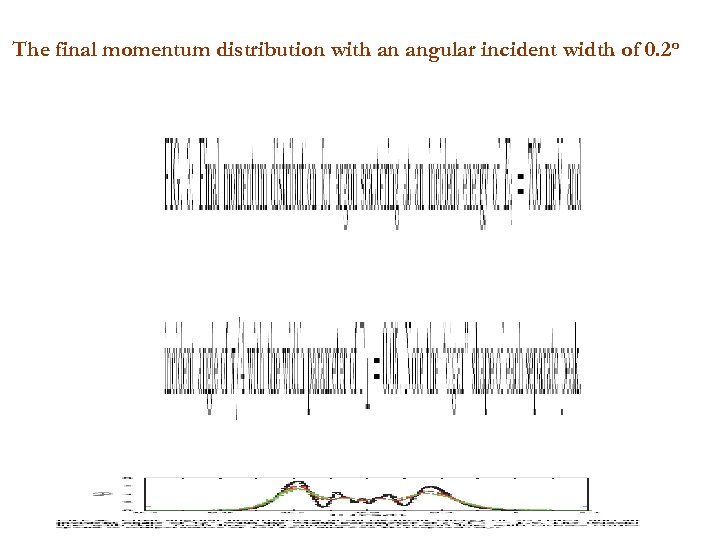
The final momentum distribution with an angular incident width of 0. 2 o
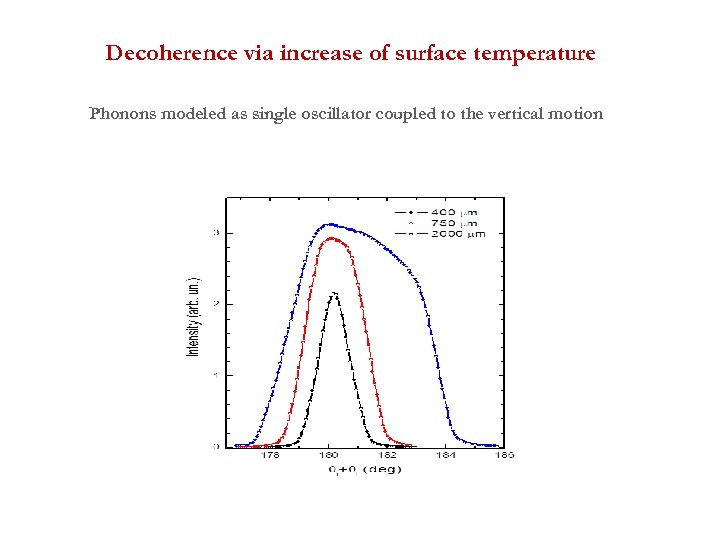
Decoherence via increase of surface temperature Phonons modeled as single oscillator coupled to the vertical motion
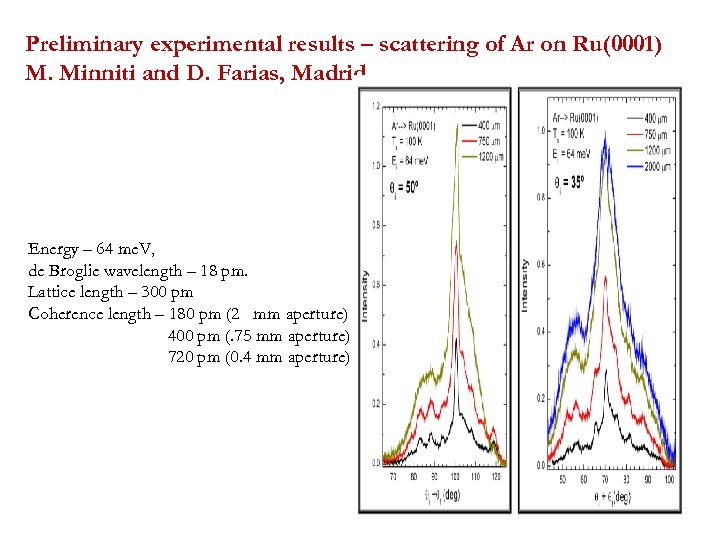
Preliminary experimental results – scattering of Ar on Ru(0001) M. Minniti and D. Farias, Madrid. Energy – 64 me. V, de Broglie wavelength – 18 pm. Lattice length – 300 pm Coherence length – 180 pm (2 mm aperture) 400 pm (. 75 mm aperture) 720 pm (0. 4 mm aperture)
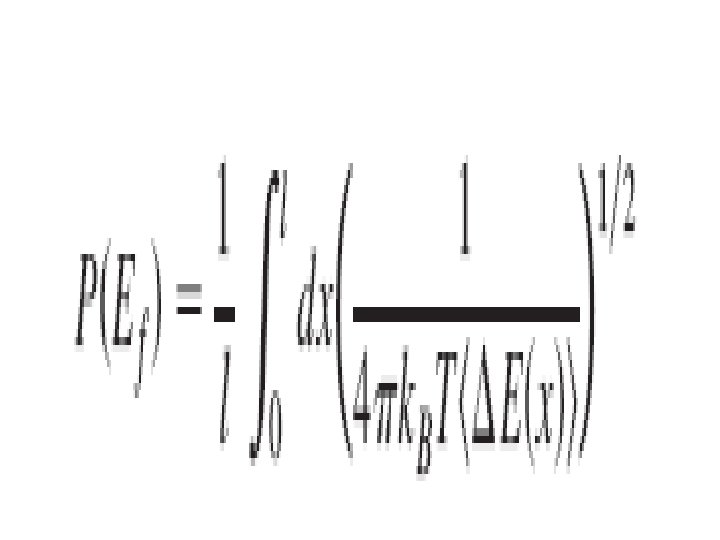
Summary: • Quantum diffraction of heavy atoms is observable in surface scattering at low temperatures. • Collimation of the incident beam leads to partial diffraction patterns. • At sufficiently low surface temperature, surface phonons do not wipe out the coherence • Decoherence may be studied quantitatively by varying the surface temperature
Future directions • Use better theory (MCTDH) to include a realistic representation for the continuum of phonon modes. • Study diffraction of molecular systems – do internal modes destroy the quantum diffraction through energy exchange? • Can heavy atom diffraction be used to study surface interactions – phonons or electronic? • Is it possible to use the quantum coherence to manipulate energy transfer with the surface? • Can one conehrently control reactive processes on the surface?
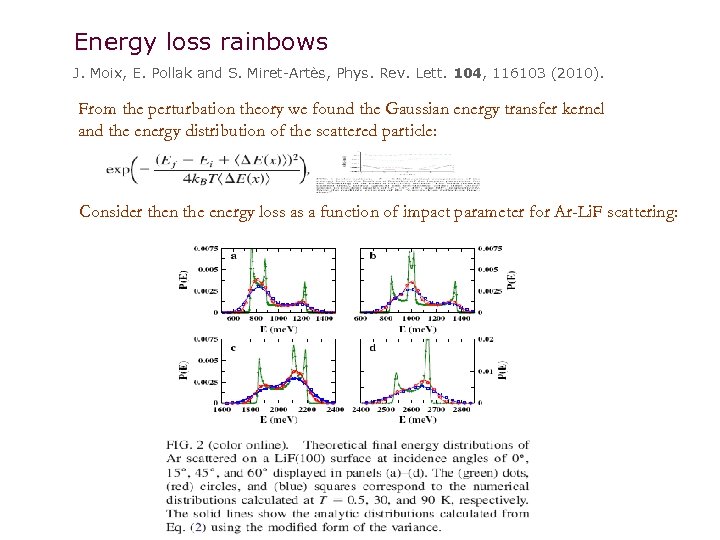
Energy loss rainbows J. Moix, E. Pollak and S. Miret-Artès, Phys. Rev. Lett. 104, 116103 (2010). From the perturbation theory we found the Gaussian energy transfer kernel and the energy distribution of the scattered particle: Consider then the energy loss as a function of impact parameter for Ar-Li. F scattering:
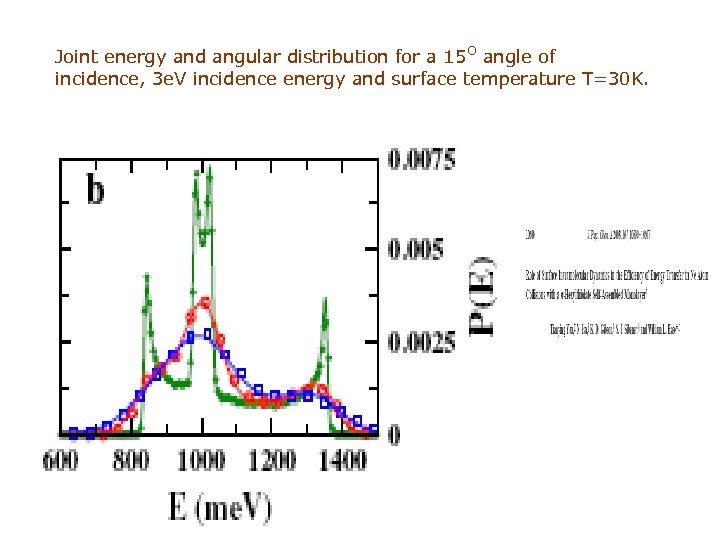
Joint energy and angular distribution for a 15 O angle of incidence, 3 e. V incidence energy and surface temperature T=30 K.
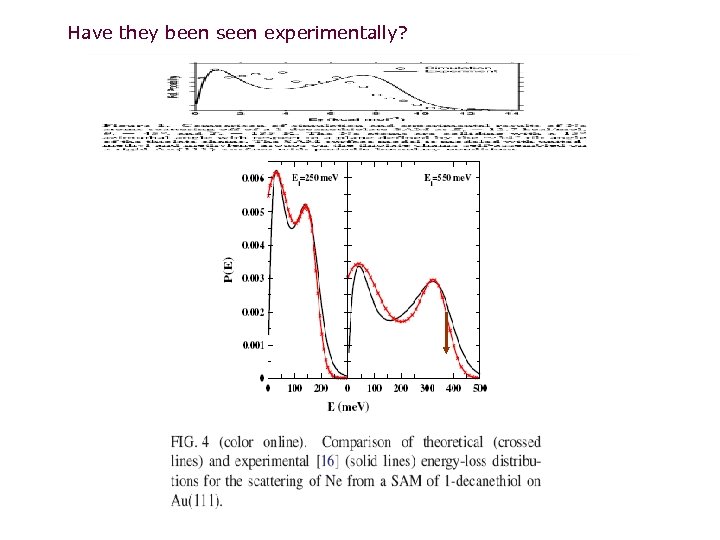
Have they been seen experimentally?
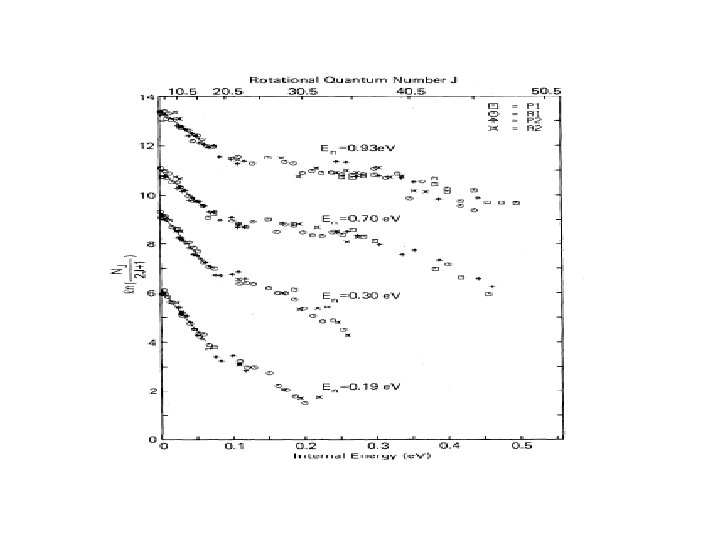
Rotational Rainbows
C 2=0. 01, C 1=0
For simplicity consider a diatomic molecule with angular momentum parallel to the surface. Let qi denote the initial angle of the diatomic axis relative to the vertical to the surface: q For a smooth surface, the interaction potential will be a function of the angle q. The final angular momentum will then depend on the initial rotational angle.
Perturbation theory The Hamiltonian: The unperturbed motion: 1 st order perturbation theory: Energy conservation:
The angular distribution: When the molecule is not too slowly rotating one readily finds: → The rotational rainbows cause maxima in the angular distribution! Examples: → Morse potential (C 1=0 for a homonuclear diatomic)
Скачать презентацию Heavy Atom Quantum Diffraction by Scattering from Surfaces
5a4b1362eeca010cdd8dbf9f9d9a588b.ppt