Heat Transfer in Microchannels 11 1 Introduction Applications

Heat Transfer in Microchannels 11. 1 Introduction: Applications Cooling of microelectronics Inkjet printer Medical research Micro-electro-mechanical systems (MEMS): Micro heat exchangers, mixers, pumps, turbines, sensors and actuators 1

11. 1. 1 Continuum and Thermodynamic Equilibrium Hypothesis Properties: (pressure, temperature, density, etc) are macroscopic manifestation of molecular activity Continuum: material having sufficiently large number of molecules in a given volume to give unique values for properties Validity of continuum assumption: the molecular-mean -free path, , is small relative to the characteristic dimension of the system Mean-free-path: average distance traveled by molecules before colliding 2

Knudson number Kn: (1. 2) = characteristic length Gases: the criterion for the validity of the continuum assumption is: (1. 3 a) Thermodynamic equilibrium: depends on collisions frequency of molecules. The condition for thermodynamic equilibrium is: (1. 3 b) 3

Microchannels: Channels where the continuum assumption and/or thermodynamic equilibrium break down 4

9. 1. 2. Surface Forces. Examine ratio of surface to volume for tube: (11. 1) For D = 1 m, A/V = 4 (1/m) For D = 1 μm, A/V = 4 x 10 6 (1/m) Consequence: (1) Surface forces may alter the nature of surface boundary conditions (2) For gas flow, increased pressure drop results in large density changes. Compressibility becomes important 5

9. 1. 3 Chapter Scope Classification Gases vs. liquids Surface boundary conditions Heat transfer in Couette flow Heat transfer in Poiseuille flow 9. 2 Basic Consideration 9. 2. 1 Mean Free Path. For gases: (11. 2) 6

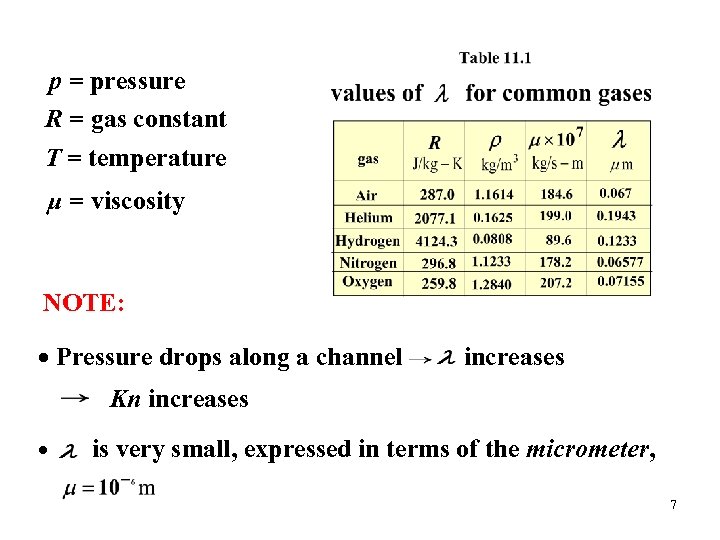p = pressure R = gas constant T = temperature μ = viscosity NOTE: Pressure drops along a channel increases Kn increases • is very small, expressed in terms of the micrometer, 7

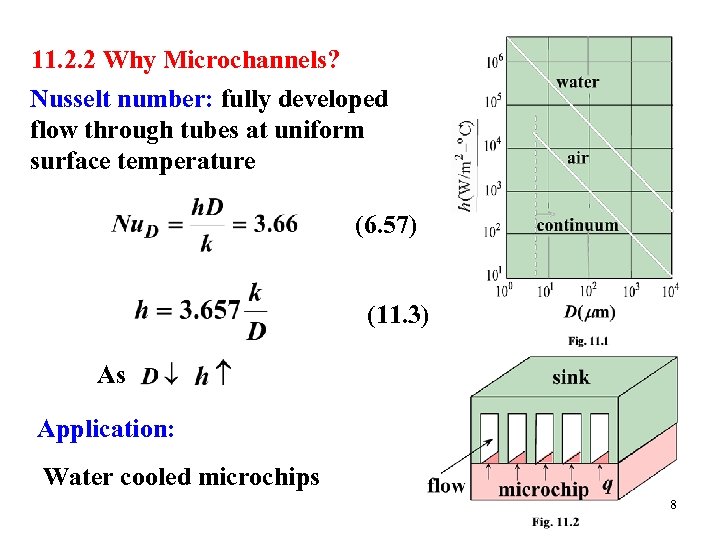11. 2. 2 Why Microchannels? Nusselt number: fully developed flow through tubes at uniform surface temperature (6. 57) (11. 3) As Application: Water cooled microchips 8

11. 2. 3 Classification Based on the Knudsen number: (11. 4) Four important factors: (1) Continuum (2) Thermodynamic equilibrium (3) Velocity slip (4) Temperature jump 9

(1) Kn < 0. 001: Macro-scale regime (previous chapters): Continuum: valid Thermodynamic equilibrium: valid No velocity slip No temperature jump (2) 0. 001 < Kn < 0. 1: Slip flow regime: Continuum: valid Thermodynamic equilibrium: fails • Velocity slip • Temperature jump Continuity, Navier-Stokes equations, and energy equations are valid No-velocity slip and No-temperature jump conditions, conditions fail Reformulate boundary conditions 10

(3) 0. 1< Kn<10: Transition flow: Continuity and thermodynamic equilibrium fail Reformulate governing equations and boundary conditions Analysis by statistical methods (4) Kn>10: Free molecular flow: analysis by kinetic theory of gases 11. 2. 4 Macro and Microchannels Macrochannels: Continuum domain, no velocity slip, no temperature jump Microchannels: Temperature jump and velocity slip, with or without failure of continuum assumption 11

Distinguishing factors: (1) Two and three dimensional effects (2) Axial conduction (3) Viscous dissipation (4) Compressibility (5) Temperature dependent properties (6) Slip velocity and temperature (7) Dominant role of surface forces 12

11. 2. 5 Gases vs. Liquids Macro convection: No distinction between gases and liquids Solutions for both are the same for the same geometry, governing parameters (Re, Pr, Gr, …) and boundary conditions Micro convection: Flow and heat transfer of gases differ from liquids Gas and liquid characteristics: (1) Mean free path: Continuum assumption may hold for liquids but fail for gases 13

Typical MEMS applications: continuum assumption is valid for liquids (2) Knudsen number: used as criterion for thermodynamic equilibrium and continuum for gases but not for liquids (3) Onset of failure of thermodynamic equilibrium and continuum: not well defined for liquids (4) Surface forces: liquid forces are different from gas forces (5) Boundary conditions: differ for liquids from gases (6) Compressibility: liquids are almost incompressible while gases are not (7) Flow physics: liquid flow is not well known. Gas flow is well known 14

(8) Analysis: more complex for liquids than gases 11. 3 General Features Flow and heat transfer phenomena change as channel size is reduced: Rarefaction: Knudsen number effect Compressibility: Effect of density change due to pressure drop along channel Viscous dissipation: Effect of large velocity gradient Examine: Effect of channel size on: Velocity profile Flow rate 15

Friction factor Transition Reynolds number Nusselt number Consider: Fully developed microchannel gas flow as the Knudsen number increases from the continuum through the slip flow domain 16

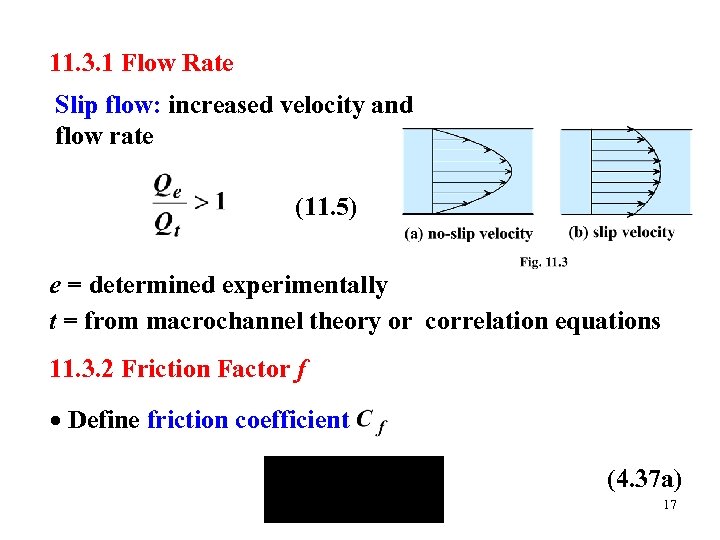11. 3. 1 Flow Rate Slip flow: increased velocity and flow rate (11. 5) e = determined experimentally t = from macrochannel theory or correlation equations 11. 3. 2 Friction Factor f Define friction coefficient (4. 37 a) 17

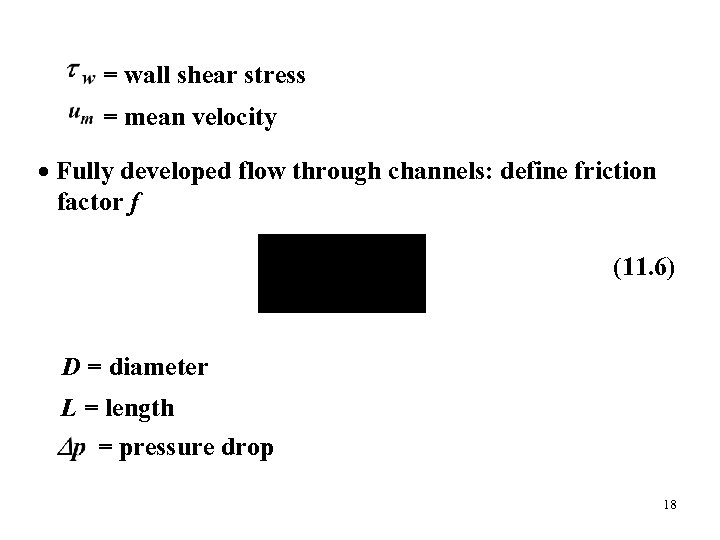= wall shear stress = mean velocity Fully developed flow through channels: define friction factor f (11. 6) D = diameter L = length = pressure drop 18

Macrochannels: fully developed laminar flow: (1) f is independent of surface roughness (2) Product of f and Reynolds number is constant for each channel geometry: (11. 7) Po = Poiseuille number (3) Po is independent of Reynolds number Microchannels: compare experimental data, theoretical value, , with , (macroscopic, continuum) 19

(11. 8) Conclusion: (1) departs from unity: (2) Unlike macrochannels, Po for fully developed flow depends on the Re (3) Conflicting findings due to: difficulties in measurements of channel size, surface roughness, pressure distribution, uncertainties in entrance effects, transition, and determination of properties 20

11. 3. 3 Transition to turbulent flow Macrochannels: smooth macrotubes (6. 1) Microchannels: reported transition Factors affecting the determination of Variation of fluid properties Measurements accuracy Surface roughness 21

11. 3. 4 Nusselt number. For fully developed conditions: Macrochannel: Nusselt number is constant Microchannels: In general, Nusselt number is not well established: Nu varies along microchannels Nu depends on: Surface roughness Reynolds number Nature of gas Widely different reported results: (11. 9) 22

where: = experimental = macrochannel theory Factors affecting the determination of Variation of fluid properties Measurements accuracy 23

11. 4 Governing Equations Slip flow regime: Factors to be considered: Compressibility Axial conduction Dissipation 11. 4. 1 Compressibility: Expressed in terms of Mach number M= 24

Macrochannels: Incompressible flow, M < 1 Linear pressure drop Microchannels: Compressible flow Non-linear pressure drop Decrease in Nusselt number 11. 4. 2 Axial Conduction Macrochannels: neglect axial conduction for (6. 30) 25

Pe = Peclet number Microchannels: low Peclet numbers, axial conduction may be important, it increases the Nusselt number 11. 4. 3 Dissipation Microchannels: large velocity gradient, dissipation may become important 11. 5 Slip Velocity and Temperature Jump Boundary Conditions Slip velocity for gases: (11. 10) 26

= fluid axial velocity at surface axial velocity x = axial coordinate n = normal coordinate measured from the surface = tangential momentum accommodating coefficient Temperature jump for gases (11. 11) T(x, 0) = fluid temperature at the boundary = surface temperature 27

, specific heat ratio = energy accommodating coefficient NOTE (1) Eq. (11. 10) and (11. 11) are valid for gases (2) Eq. (11. 10) and (11. 11) are valid for Kn < 0. 1 (3) σu and σT, are: • Empirical factors • They depend on the gas, geometry and surface • Values range from zero (perfectly smooth) to unity 28

• Difficult to determine experimentally • Values for various gases are approximately unity 29

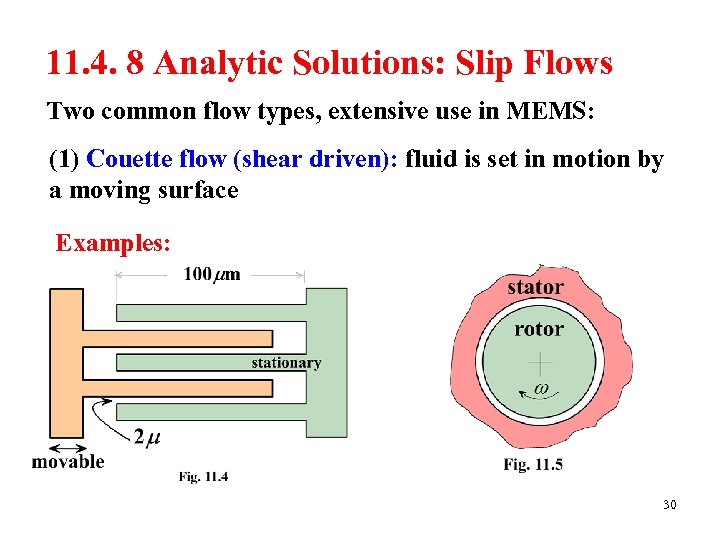11. 4. 8 Analytic Solutions: Slip Flows Two common flow types, extensive use in MEMS: (1) Couette flow (shear driven): fluid is set in motion by a moving surface Examples: 30

(2) Poiseuille flow (pressure driven): fluid is set in motion by an axial pressure gradient Examples: Micro heat exchangers, mixers, microelectronic heat sinks NOTE No pressure drop in Couette flow Signifiant pressure drop in Poiseuille flow Boundary conditions: two types: (1) Uniform surface temperature (2) Uniform surface heat flux 31

11. 6. 1 Assumptions (1) Steady state (2) Laminar Flow (3) Two-dimensional (4) Slip flow regime (0. 001 < Kn < 0. 1) (5) Ideal gas (6) Constant viscosity, conductivity and specific heats (7) Negligible lateral variation of density and pressure (8) Negligible dissipation (unless otherwise stated) (9) Negligible gravity 32

(10) The accommodation coefficients are equal to unity, 11. 6. 2 Couette Flow with Viscous Dissipation: Parallel Plates with Surface Convection Infinitely large parallel plates Gas fills gap between plates Upper plate: moves with velocity us Lower plate: stationary, insulated Convection at the upper plate Consider dissipation and slip conditions 33

Determine: (1) Velocity distribution (2) Mass flow rate (3) Nusselt number Find flow field and temperature distribution Flow Field Normal velocity and all axial derivatives vanish Axial component of the Navier-Stokes equations, (2. 9), simplifies to (11. 12) 34

Boundary conditions: use (11. 10), Set • Lower plate: n = y = 0 and (11. 10) gives (g) Upper plate: n = H – y, (9. 10) gives (h) Solution (11. 14) 35

Kn is the local Knudsen number (11. 13) NOTE (1) Fluid velocity at the moving plate: set y = H in (11. 14) Effect of slip: Decrease fluid velocity at the moving plate Increase fluid velocity at the stationary plate 36

(2) Velocity distribution is linear (3) Setting Kn = 0 in (11. 14) gives the no-slip solution (k) Mass Flow Rate m (11. 15) W = channel width Neglect variation of ρ along y, (11. 14) into (11. 15) 37

(11. 16) Flow rate is independent of the Knudsen number Compare with macrochannel flow rate mo (k) into (11. 15) (11. 17) This is identical to (11. 16), thus (11. 18) 38

Nusselt Number • Equivalent diameter for parallel plates, De = 2 H • Nusselt number (l) Heat transfer coefficient h: 39

(11. 19) k = conductivity of fluid T = fluid temperature Ts = plate temperature NOTE (1) Fluid temperature at the moving plate, T (x, H), is not equal to surface temperature (2) h is defined in terms of surface temperature Ts 40

(3) Use temperature jump, (11. 11), to determine Ts (4) For the upper plate, n =H – y, eq. (11. 11) gives (11. 20) • Mean temperature Tm: defined in Section 6. 6. 2 (11. 21) • Neglect variation of cp and ρ along y, use (11. 14). for u and (11. 15) for m 41

(11. 22) Determine temperature distribution: Use energy equation, (2. 15) Apply above assumptions, note that axial derivatives vanish, (2. 15) gives (11. 23) 42

(2. 17) gives the dissipation function which simplifies to (11. 24) (9. 24) into (9. 23) (11. 25) Boundary conditions Lower plate: (m) 43

Upper plate: Use (920) to eliminate Ts (n) Use velocity solution (9. 14), solve for T (11. 26) 44

where (p) Velocity solution (11. 14), temperature solution (11. 26) give. Ts , Tm and Nu (u) (w) 45

(11. 27) Note the following regarding the Nusselt number (1) It is independent of Biot number (2) It is independent of the Reynolds number (3) Unlike macrochannels, it depends on the fluid (4) First two terms in the denominator of (11. 27) represent rarefaction (Knudsen number). The second term represents effect of temperature jump 46

(5) Nusselt number for macrochannels, Nuo: set Kn = 0 in (11. 27): (11. 28) Ratio of (11. 27) and (11. 28) (11. 29) NOTE: Ratio is less than unity 47

11. 6. 3 Fully Developed Poiseuille Channel Flow: Uniform Surface Flux Pressure driven flow between parallel plates Fully developed velocity and temperature Inlet and outlet pressures are pi and po • Uniform surface flux, Determine: (1) Velocity distribution (2) Pressure distribution (3) Mass flow rate (4) Nusselt number 48

Note: Major difference between macro and micro fully developed slip flow: Macrochannels: incompressible flow (1) Parallel streamlines (2) Zero lateral velocity component (v = 0) (3) Invariant axial velocity (4) Linear axial pressure 49

Microchannels: compressibility and rarefaction change above flow pattern: (1) None of above conditions hold (2) Large axial pressure drop compressible flow density changes (3) Rarefaction: pressure decreases Kn increases with x increases (4) Axial velocity varies with axial distance (5) Lateral velocity v does not vanish (6) Streamlines are not parallel (7) Pressure gradient is not constant 50

Assumptions (1) Steady state (2) Laminar flow (3) (4) Two-dimensional (5) Slip flow regime (0. 001 < Kn < 0. 1) (6) Ideal gas (7) Constant viscosity, conductivity and specific heats (8) Negligible lateral variation of density and pressure (9) 51

(10) Negligible dissipation Flow Field Additional assumptions: (11) Isothermal flow (12) Negligible inertia forces: =0 (13) The dominant viscous force is Navier-Stokes equations (2. 9) simplify to: (c) 52

Boundary conditions: Symmetry at y = 0 (e) For the upper plate, n = H – y (f) Solution to u (11. 30) 53

For an ideal gas (11. 33) Pressure Distribution p: To determine p(x), must determine vertical component v: start with continuity (2. 2 a) Apply above assumptions 54

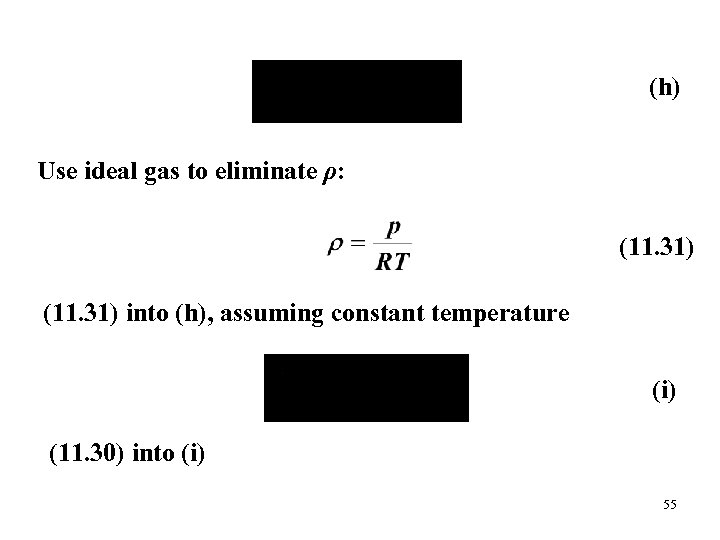(h) Use ideal gas to eliminate ρ: (11. 31) into (h), assuming constant temperature (i) (11. 30) into (i) 55

(j) Boundary conditions: (k) (l) Multiply (j) by dy, integrate and using (k) (m) 56

Evaluate the integrals (11. 32) Determination of p(x): Apply boundary condition (l) to (11. 32) (n) Express Kn in terms of pressure. Equations (11. 2) and (11. 13) give (11. 33) 57

Evaluate (n) at y = H/2, substitute (11. 33) into (n) and integrate Integrate again (T is assumed constant) (o) Solve for p (p) 58

Pressure boundary conditions , (q) Apply (q) to (p) Substitute into (p) and normalize by po 59

(r) Introduce outlet Knudsen number Kno using (11. 2) and (11. 13) (11. 34) Substitute (11. 34) into (r) (11. 35) 60

NOTE: (1) Unlike macrochannel Poiseuille flow, pressure variation along the channel is non-linear (2) Knudsen number terms represent rarefaction effect (3) The terms (pi/po)2 and [1 - (pi/po)2](x/L) represent the effect of compressibility (4) Application of (11. 35) to the limiting case of Kno =0 gives (11. 36) This result represents the effect of compressibility alone 61

Mass Flow Rate (s) W = channel width (11. 30) in (s) (t) Density ρ : (11. 37) 62

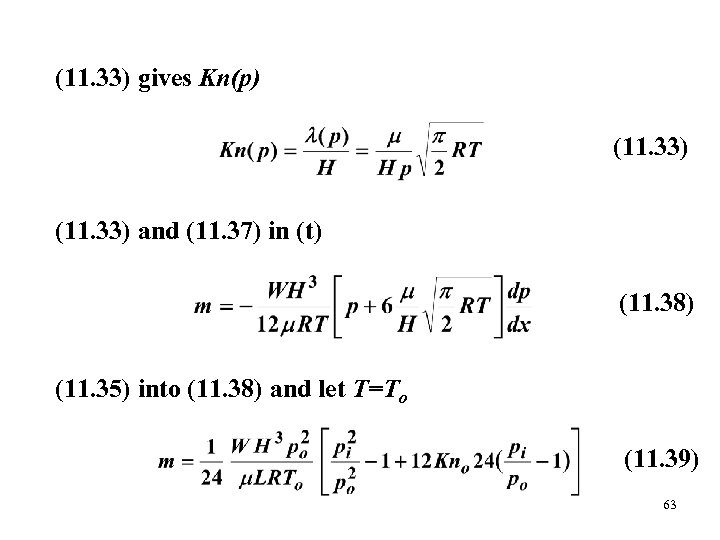(11. 33) gives Kn(p) (11. 33) and (11. 37) in (t) (11. 38) (11. 35) into (11. 38) and let T=To (11. 39) 63

Compare with no-slip, incompressible macrochannel case: (11. 40) Taking the ratio (11. 41) NOTE (1) Microchannels flow rate is very sensitive to H (2) (11. 39) shows effect of rarefaction (slip) and compressibility on m 64

(3) Since (11. 41) shows that neglecting compressibility and rarefaction underestimates m Nusselt Number (u) For uniform surface flux Substitute into (g) (v) 65

Plate temperature Ts: use (11. 11) (11. 42) Mean temperature Tm: (11. 43) Need u(x, y) and T(x, y) Velocity distribution: (11. 30) gives u(x, y) for isothermal 66 flow

Additional assumption: (14) Isothermal axial velocity solution is applicable (15) No dissipation, (16) No axial conduction, (17) Negligible effect of compressibility on the energy equation (18) Nearly parallel flow, Energy equation: equation (2. 15) simplifies to (11. 44) 67

Boundary conditions: (w) (x) To solve (11. 44), assume: (19) Fully developed temperature Solution: T(x, y) and Tm(x): Define (11. 45) 68

Fully developed temperature: is independent of x (11. 46) Thus (11. 47) (11. 45) and (11. 46) give 69

Expanding and use (11. 45) (11. 48) Determine: and Heat transfer coefficient h: (y) 70

(11. 42) gives Ts(x). (11. 45) gives temperature gradient in (y) Differentiate (z) into (y), use (11. 42) for Ts(x) (11. 49) 71

Newton’s law of cooling: Equate with (11. 49) (11. 50) Differentiate Combine this with (11. 48) 72

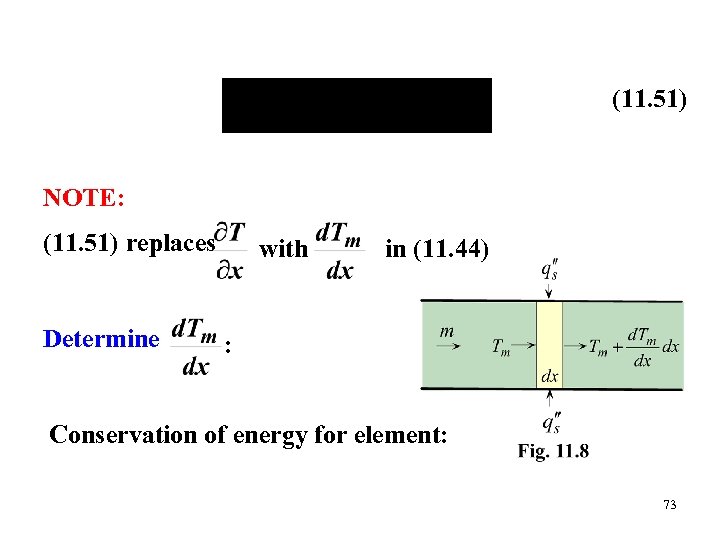(11. 51) NOTE: (11. 51) replaces Determine with in (11. 44) : Conservation of energy for element: 73

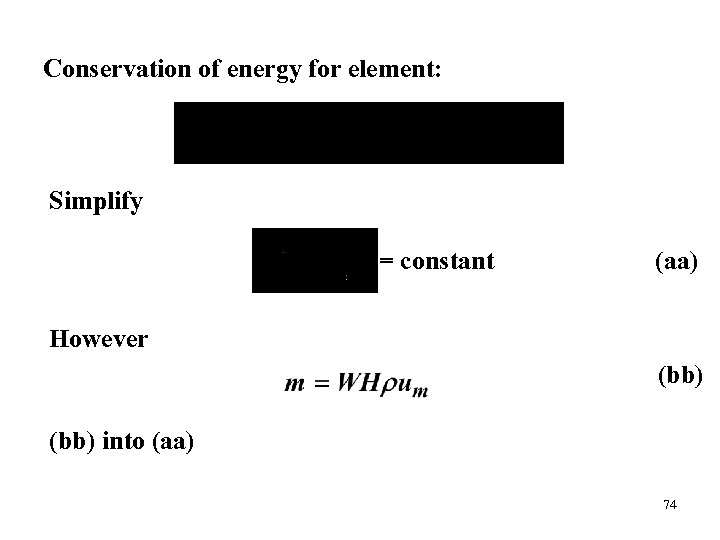Conservation of energy for element: Simplify = constant (aa) However (bb) into (aa) 74

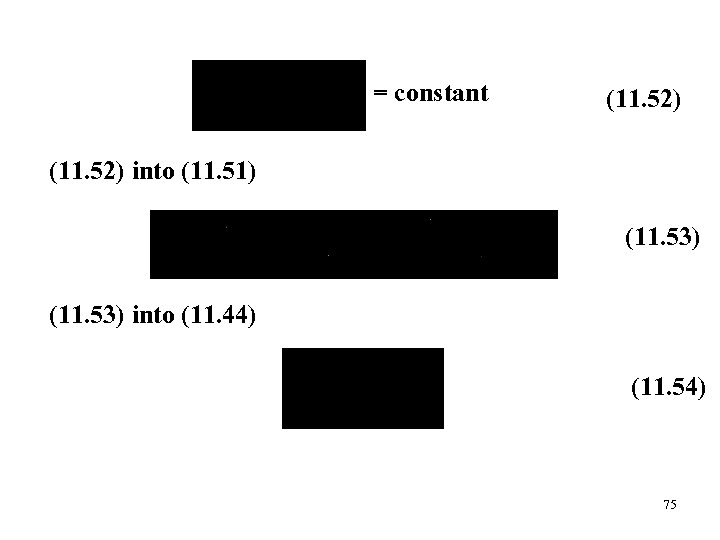= constant (11. 52) into (11. 51) (11. 53) into (11. 44) (11. 54) 75

Mean velocity: (cc) (11. 30) gives velocity u. (11. 30) into (cc) Integrate (11. 55) 76

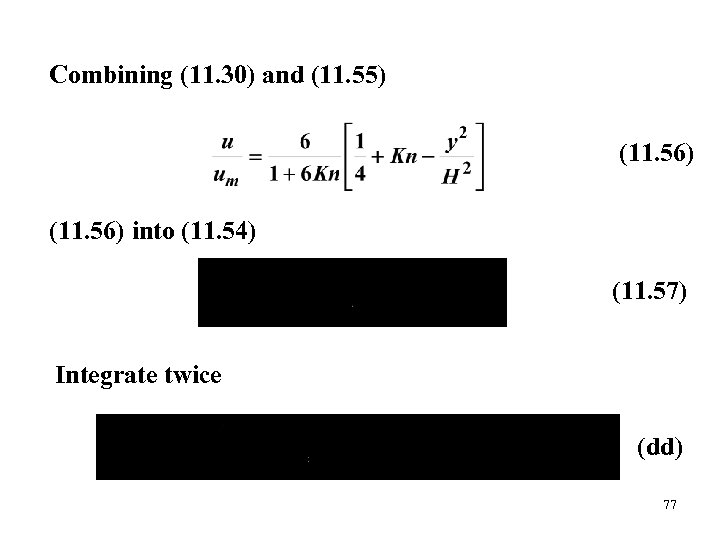Combining (11. 30) and (11. 55) (11. 56) into (11. 54) (11. 57) Integrate twice (dd) 77

f(x) and g(x) are “constants” of integration Boundary condition (w) gives Solution (dd) becomes (11. 58) NOTE: (1)Boundary condition (x) is automatically satisfied (2) g(x) is determine by formulating Tm using two methods 78

Method 1: Integrate (11. 52) where (11. 59) Evaluate the integrals (11. 60) 79

Method 2: Use definition of Tm. Substitute (11. 30) and (11. 58) into (11. 43) Evaluate the integrals (11. 61) Equating (11. 60) and (11. 61) gives g(x) (11. 62) 80

(11. 58) into (11. 42) gives Ts (11. 63) The Nusselt number is given in (v) (11. 61) and (11. 63) into (v) (11. 64) 81

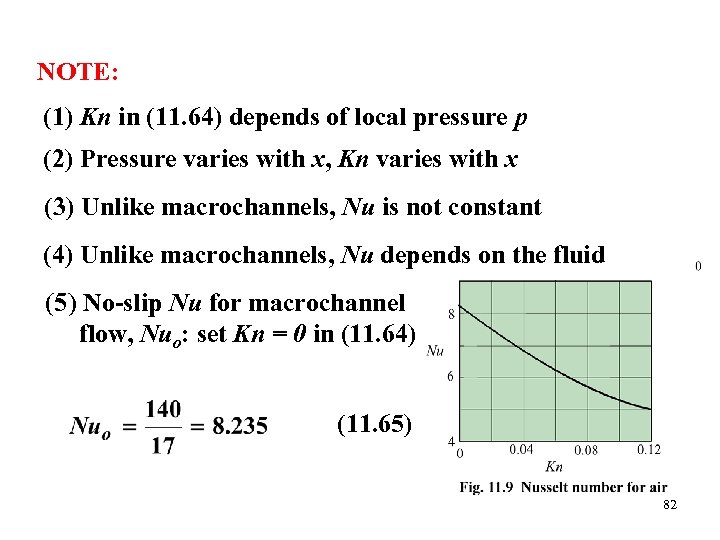NOTE: (1) Kn in (11. 64) depends of local pressure p (2) Pressure varies with x, Kn varies with x (3) Unlike macrochannels, Nu is not constant (4) Unlike macrochannels, Nu depends on the fluid (5) No-slip Nu for macrochannel flow, Nuo: set Kn = 0 in (11. 64) (11. 65) 82

This agrees with Table 6. 2 (6) Rarefaction and compressibility decrease the Nusselt number 83

11. 6. 4 Fully Developed Poiseuille Channel Flow: Uniform Surface Temperature Repeat Section 11. 6. 3 with plates at uniform surface temperature Ts Flow field: same for both cases: (11. 30) u(y) (11. 35) m Energy equation: (11. 44) is modified to include axial conduction 84

Boundary conditions: different for the two cases Nusselt number: (11. 66 a) Need T(x, y) and Tm(x) Solution approach: Solve the Graetz channel entrance problem and set to obtain the fully developed solution 85

Axial conduction: can be neglected for: (7. 50) Microchannels: Small Reynolds Small Peclet number Axial conduction is important Include axial conduction: modify energy equation (11. 44) (11. 67 a) 86

Boundary and inlet conditions: (11. 68 a) (11. 69 a) (11. 70 a) (11. 71 a) 87

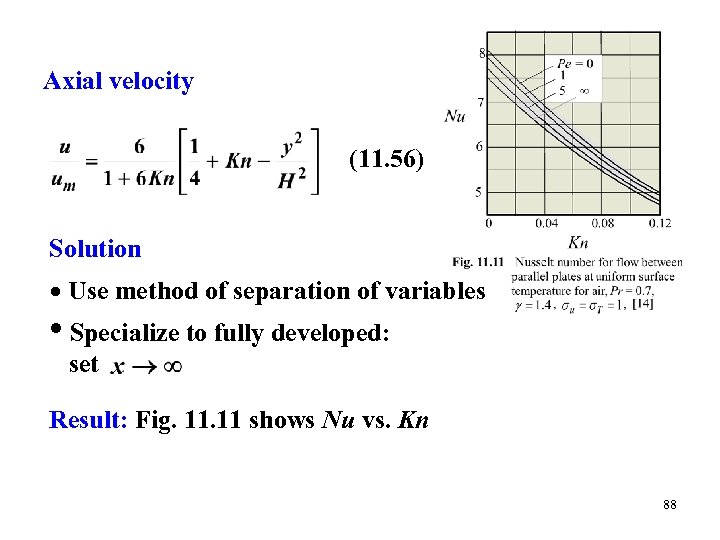Axial velocity (11. 56) Solution Use method of separation of variables • Specialize to fully developed: set Result: Fig. 11 shows Nu vs. Kn 88

NOTE (1) Nu decreases as the Kn is increased (2) No-slip solution overestimates microchannels Nu (3) Axial conduction increases Nu (4) Limiting case: no-slip (Kn = 0) and no axial conduction : (11. 73) This agrees with Table 6. 2 Heat Transfer Rate, : Following Section 6. 5 89

(6. 14) Tm (x) is given by (6. 13) is determine numerically using (6. 12) 90

11. 6. 5 Fully Developed Poiseuille Flow in Micro Tubes: Uniform Surface Flux Consider: Poiseuille flow in micro tube Uniform surface flux Fully developed velocity and temperature • Inlet and outlet pressures are pi and po 91

Determine (1) Velocity distribution (2) Nusselt number Rarefaction and compressibility affect flow and heat transfer Velocity slip and temperature jump Axial velocity variation Lateral velocity component Non-parallel stream lines Non-linear pressure 92

Assumptions Apply the 19 assumptions of Poiseuille flow between parallel plates (Sections 11. 6. 3) Flow Field Follow analysis of Section 11. 6. 3 Axial component of Navier-Stokes equations in cylindrical coordinates: (a) = axial velocity 93

Boundary conditions: Assume symmetry and set σu = 1 (b) (c) Solution (11. 74) 94

Knudsen number (11. 75) Mean velocity vzm Use (11. 74), integrate (11. 76) 95

(11. 74) and (11. 76) (11. 77) Solution to axial pressure (11. 78) (11. 76) and (11. 78) give m (11. 79 a) 96

For incompressible no-slip (macroscopic) (11. 79 b) Nusselt Number Follow Section 11. 6. 3 (d) Heat transfer coefficient h: 97

Substituting into (d) (e) Ts = tube surface temperature, obtained from temperature jump condition (11. 11) (f) Mean temperature: (11. 80) 98

Energy equation: (11. 81) Boundary conditions: (g) (h) Define 99

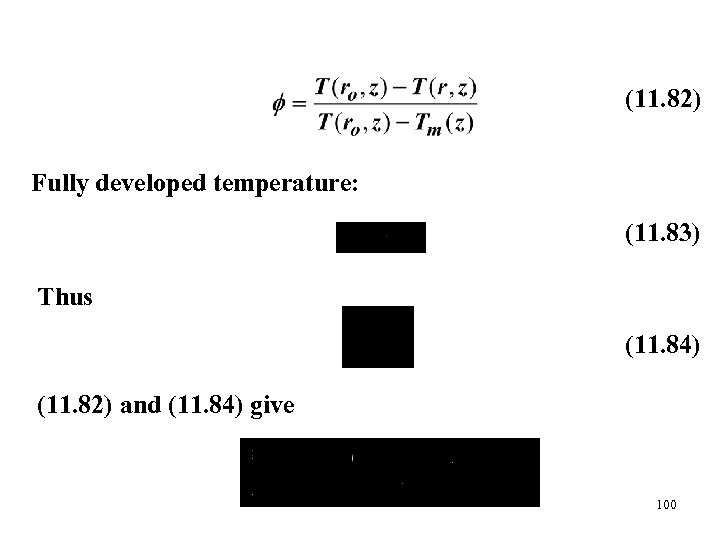(11. 82) Fully developed temperature: (11. 83) Thus (11. 84) (11. 82) and (11. 84) give 100

Expand (11. 82) (11. 85) Determine: and Heat transfer coefficient h, : (i) 101

Rewrite (11. 81) Differentiate and evaluating at (j) into (i) (k) 102

Newton’s law of cooling h Equate with (k) (11. 86) Differentiate 103

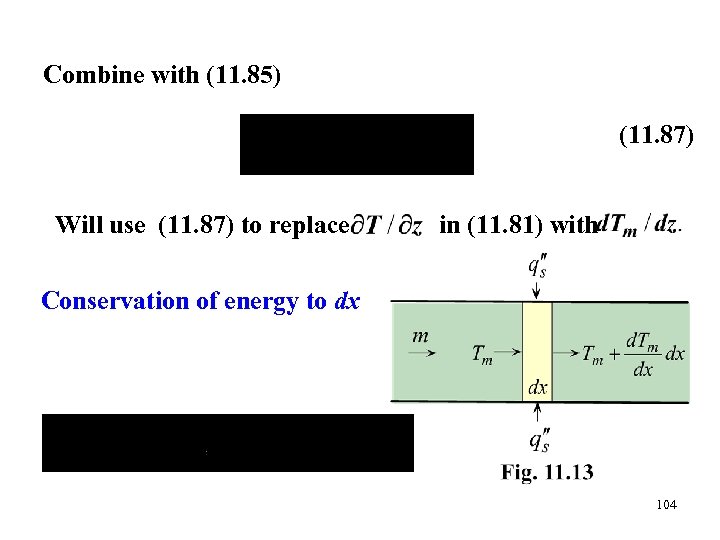Combine with (11. 85) (11. 87) Will use (11. 87) to replace in (11. 81) with Conservation of energy to dx 104

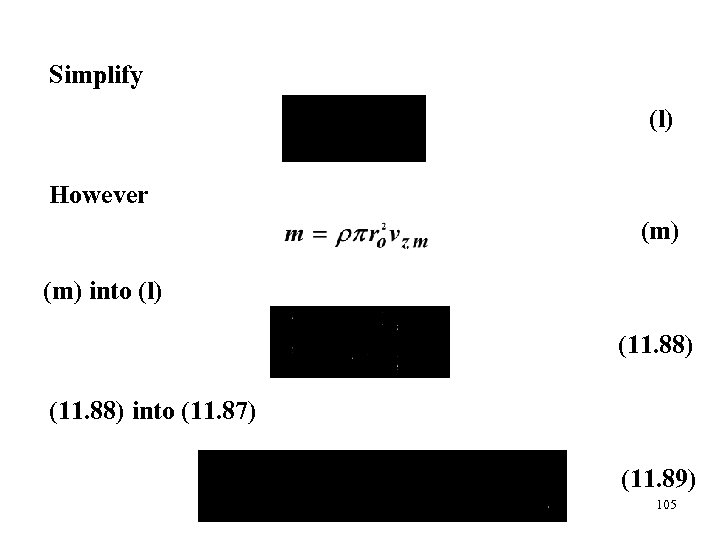Simplify (l) However (m) into (l) (11. 88) into (11. 87) (11. 89) 105

(11. 89) into (11. 81) (11. 90) (11. 77) is used to eliminate in the above (11. 91) Integrate (n) 106

Condition (g) gives Solution (n) becomes (11. 92) Condition (h) is automatically satisfied Determine g(z): Use two methods to determine Tm Method 1: Integrate (11. 88) 107

where (11. 93) Evaluate the integral (11. 94) Method 2: Use definition of Tm in (11. 80). Substitute (11. 74) and (11. 92) into (11. 80) 108

Integrate (11. 95) Equate (11. 94) and (11. 95), solve for g(z) (11. 96) 109

Use (f) and (11. 92) to determine (11. 97) Nusselt number: (11. 95) and (11. 97) into (e) (11. 98) 110

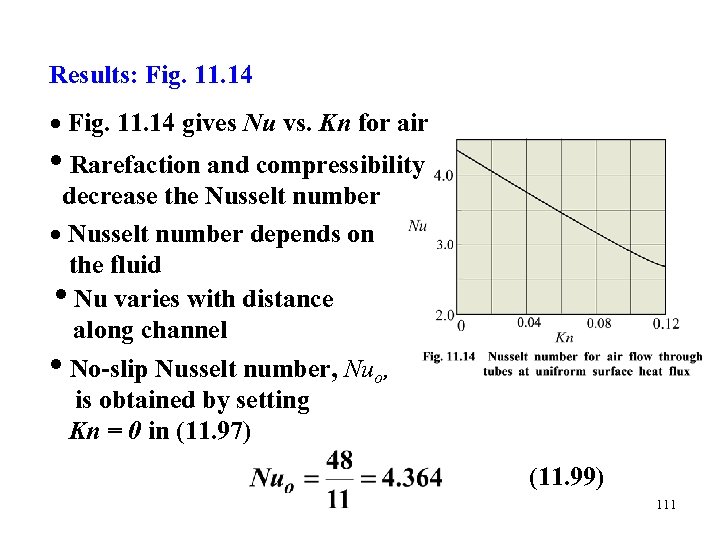Results: Fig. 11. 14 gives Nu vs. Kn for air • Rarefaction and compressibility decrease the Nusselt number depends on the fluid • Nu varies with distance along channel • No-slip Nusselt number, Nuo, is obtained by setting Kn = 0 in (11. 97) (11. 99) 111

This agrees with (6. 55) for macro tubes 11. 9. 6 Fully Developed Poiseuille Flow in Micro Tubes: Uniform Surface Temperature • Repeat Section 11. 6. 5 with the tube at surface temperature Ts Apply same assumptions Boundary conditions are different Flow field solution is identical for the two cases 112

Nusselt number: (11. 100 a) • Determine T(r, z) and Tm(z) Follow the analysis of Section 11. 6. 4 Solution is based on the limiting case of Graetz tube entrance problem Axial conduction is taken into consideration Energy equation (11. 81) is modified to include axial conduction: 113

(11. 101 a) Boundary and inlet conditions (11. 102 a) (11. 103 a) (11. 104 a) (11. 105 a) 114

(11. 76) gives axial velocity (11. 76) Solution by the method of separation of variables Solution is specialized for fully developed conditions at large z • Result for air shown in Fig. 11. 16 Neglecting axial conduction: set Axial conduction increases the Nu 115

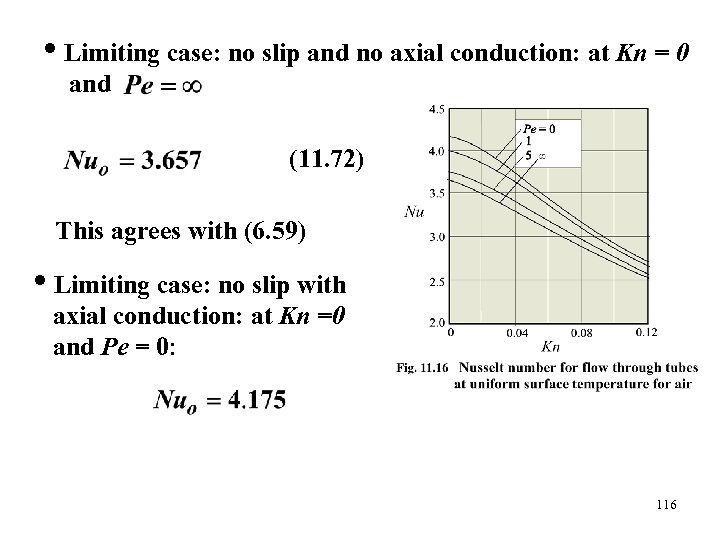• Limiting case: no slip and no axial conduction: at Kn = 0 and (11. 72) This agrees with (6. 59) • Limiting case: no slip with axial conduction: at Kn =0 and Pe = 0: 116