d8ec9a105f65d73cea7e10f4bf3b025c.ppt
- Количество слайдов: 78
![Hardware (Part A) v Reading Materials: o Chapter 4 of [SG]: The Building Blocks Hardware (Part A) v Reading Materials: o Chapter 4 of [SG]: The Building Blocks](https://present5.com/presentation/d8ec9a105f65d73cea7e10f4bf3b025c/image-1.jpg) Hardware (Part A) v Reading Materials: o Chapter 4 of [SG]: The Building Blocks of HW o Optional: Chapter 1 of [Brookshear] OUTLINE 1. The Binary Digital Computer 1. Organization of Digital Computers 2. Binary Numbers 3. Boolean Logic and Basic Gates 4. Basic Circuit Design (UIT 2201: Hardware(a)) Page 1 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Hardware (Part A) v Reading Materials: o Chapter 4 of [SG]: The Building Blocks of HW o Optional: Chapter 1 of [Brookshear] OUTLINE 1. The Binary Digital Computer 1. Organization of Digital Computers 2. Binary Numbers 3. Boolean Logic and Basic Gates 4. Basic Circuit Design (UIT 2201: Hardware(a)) Page 1 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Chapter Objectives v In this chapter, you will learn about o o v The Binary Numbering System Boolean Logic and Basic Gates Building Simple Computer Circuits Simple Control Circuits This chapter focus on logic design o How to represent and store information o Applying symbolic logic to design gates o Using gates to build circuits for addition, compare, simple control (UIT 2201: Hardware(a)) Page 2 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Chapter Objectives v In this chapter, you will learn about o o v The Binary Numbering System Boolean Logic and Basic Gates Building Simple Computer Circuits Simple Control Circuits This chapter focus on logic design o How to represent and store information o Applying symbolic logic to design gates o Using gates to build circuits for addition, compare, simple control (UIT 2201: Hardware(a)) Page 2 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
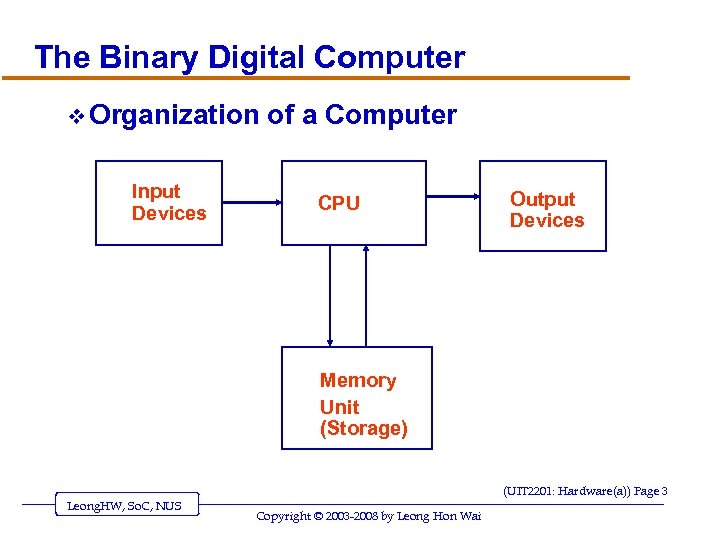 The Binary Digital Computer v Organization Input Devices of a Computer CPU Output Devices Memory Unit (Storage) (UIT 2201: Hardware(a)) Page 3 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
The Binary Digital Computer v Organization Input Devices of a Computer CPU Output Devices Memory Unit (Storage) (UIT 2201: Hardware(a)) Page 3 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Analog/Digital Computer …Up to now, whatever we have discussed could equally well be discussed in the context of either digital or analog computations… v We shall concentrate on digital computer o Specifically, binary computers o BINARY = two value (0 and 1) [ON/OFF] v Why binary computers? o Physical components – transistors, etc o Reliability of hardware components (UIT 2201: Hardware(a)) Page 4 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Analog/Digital Computer …Up to now, whatever we have discussed could equally well be discussed in the context of either digital or analog computations… v We shall concentrate on digital computer o Specifically, binary computers o BINARY = two value (0 and 1) [ON/OFF] v Why binary computers? o Physical components – transistors, etc o Reliability of hardware components (UIT 2201: Hardware(a)) Page 4 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Why use Binary Numbers? v Reliability o Represent only two values (0 and 1), ON/OFF o High margin of error v Nature of Hardware Devices o Many devices are “two-state” devices v Persistence of Digital Data o Can store and preserve digital data better (UIT 2201: Hardware(a)) Page 5 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Why use Binary Numbers? v Reliability o Represent only two values (0 and 1), ON/OFF o High margin of error v Nature of Hardware Devices o Many devices are “two-state” devices v Persistence of Digital Data o Can store and preserve digital data better (UIT 2201: Hardware(a)) Page 5 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Why Binary Computers: Reliability v Reliability: o computer store info using electronic devices o electronic quantities measured by: u voltage, current, charge, etc o These quantities are not always reliable! u esp. for old equipments u Also, the range of voltage changes with advances in hardware technology (UIT 2201: Hardware(a)) Page 6 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Why Binary Computers: Reliability v Reliability: o computer store info using electronic devices o electronic quantities measured by: u voltage, current, charge, etc o These quantities are not always reliable! u esp. for old equipments u Also, the range of voltage changes with advances in hardware technology (UIT 2201: Hardware(a)) Page 6 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Why Binary: Nature of Hardware Devices v Many hw devices are “two-state” devices o magnetized / demagnetized u diskettes (3. 5” floppy, Zip disks, …) o direction of magnetization (cw / ccw) u CORE memory (main memory) o charged / discharged capacitor (UIT 2201: Hardware(a)) Page 7 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Why Binary: Nature of Hardware Devices v Many hw devices are “two-state” devices o magnetized / demagnetized u diskettes (3. 5” floppy, Zip disks, …) o direction of magnetization (cw / ccw) u CORE memory (main memory) o charged / discharged capacitor (UIT 2201: Hardware(a)) Page 7 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Why Digital (not Analog): More Durable v Analog data poses difficulties o very hard to store real numbers accurately o or persistently (over time) o eg: old photographs, movie reels, books v Solution: Store them digitally o CD player uses approximation… u instead of the exact frequency/volume (audio) u But, the approximation is “good enough” u Our ears not sensitive enough to tell difference o Once we have digital data (reliability) u also, can use various algorithms (eg: compression) for easier processing of the data…. (UIT 2201: Hardware(a)) Page 8 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Why Digital (not Analog): More Durable v Analog data poses difficulties o very hard to store real numbers accurately o or persistently (over time) o eg: old photographs, movie reels, books v Solution: Store them digitally o CD player uses approximation… u instead of the exact frequency/volume (audio) u But, the approximation is “good enough” u Our ears not sensitive enough to tell difference o Once we have digital data (reliability) u also, can use various algorithms (eg: compression) for easier processing of the data…. (UIT 2201: Hardware(a)) Page 8 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Hardware: The Basic Building Blocks 1. The Digital Computer 2. Binary Numbers 1. 2. 3. Binary number System From Decimal to Binary Rep. of Numeric and Textual Information 4. Rep. of Sound, Image Information 5. Reliability of Binary Encoding READ: Sect. 4. 2 of [SG] or Sect 1. 4, 1. 5, 1. 7 of [A] 3. Boolean Logic and Basic Gates 4. Basic Circuit Design (UIT 2201: Hardware(a)) Page 9 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Hardware: The Basic Building Blocks 1. The Digital Computer 2. Binary Numbers 1. 2. 3. Binary number System From Decimal to Binary Rep. of Numeric and Textual Information 4. Rep. of Sound, Image Information 5. Reliability of Binary Encoding READ: Sect. 4. 2 of [SG] or Sect 1. 4, 1. 5, 1. 7 of [A] 3. Boolean Logic and Basic Gates 4. Basic Circuit Design (UIT 2201: Hardware(a)) Page 9 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 2. The Binary Numbering System v. A computer’s internal storage techniques are different from the way people represent information in daily lives v Information inside a digital computer is stored as a collection of binary data (UIT 2201: Hardware(a)) Page 10 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
2. The Binary Numbering System v. A computer’s internal storage techniques are different from the way people represent information in daily lives v Information inside a digital computer is stored as a collection of binary data (UIT 2201: Hardware(a)) Page 10 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Numbers (vs Decimal Numbers) v Humans use Decimal number system o 7809 = 7 103 + 8 102 + 0 101 + 9 100 o Each digit is from {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – Base 10 o (we happen to have 10 fingers. ) v Computers use Binary number system o (1101)2 = 1 23 + 1 22 + 0 21 + 1 20 = 13 o Each binary digit (bit) is {0, 1} – Base 2 o (IT people have 2 fingers (1 per hand)) v Readings: Section 4. 2 of [SG] (UIT 2201: Hardware(a)) Page 11 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Numbers (vs Decimal Numbers) v Humans use Decimal number system o 7809 = 7 103 + 8 102 + 0 101 + 9 100 o Each digit is from {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – Base 10 o (we happen to have 10 fingers. ) v Computers use Binary number system o (1101)2 = 1 23 + 1 22 + 0 21 + 1 20 = 13 o Each binary digit (bit) is {0, 1} – Base 2 o (IT people have 2 fingers (1 per hand)) v Readings: Section 4. 2 of [SG] (UIT 2201: Hardware(a)) Page 11 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
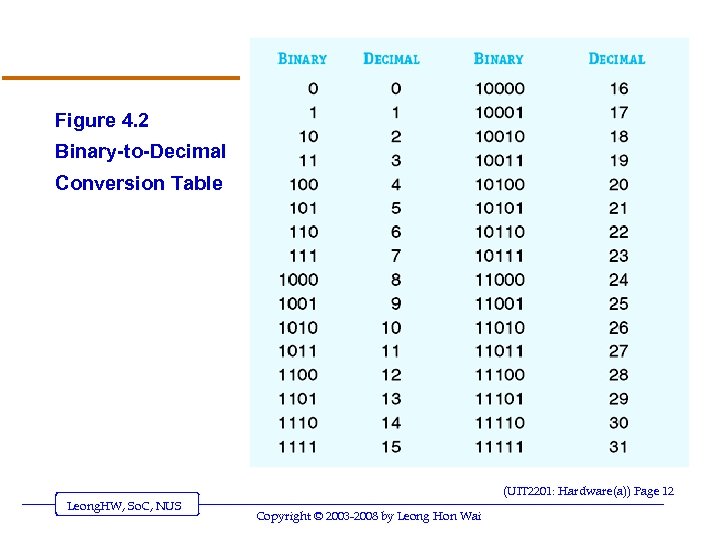 Figure 4. 2 Binary-to-Decimal Conversion Table (UIT 2201: Hardware(a)) Page 12 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 2 Binary-to-Decimal Conversion Table (UIT 2201: Hardware(a)) Page 12 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Converting from Decimal to Binary Example: 43 v Method: 43 / 2 21 / 2 10 / 2 5/2 2/2 1/2 v (43)10 (repeated divide by 2) ----> ----> Quotient: 21 Quotient: 10 Quotient: 5 Quotient: 2 Quotient: 1 Quotient: 0 Remainder: 1 Remainder: 0 Remainder: 1 = (101011)2 (UIT 2201: Hardware(a)) Page 13 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Converting from Decimal to Binary Example: 43 v Method: 43 / 2 21 / 2 10 / 2 5/2 2/2 1/2 v (43)10 (repeated divide by 2) ----> ----> Quotient: 21 Quotient: 10 Quotient: 5 Quotient: 2 Quotient: 1 Quotient: 0 Remainder: 1 Remainder: 0 Remainder: 1 = (101011)2 (UIT 2201: Hardware(a)) Page 13 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Number of Bits Needed v Have seen that (43)10 = (101011)2 v To represent decimal (43)10 in binary, we need 6 binary bits In general, to represent n (in decimal), we need k = lg n binary bits o Why? Use the above process as a guide -- we will repeatedly divide by 2 until we reach 0. (UIT 2201: Hardware(a)) Page 14 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Number of Bits Needed v Have seen that (43)10 = (101011)2 v To represent decimal (43)10 in binary, we need 6 binary bits In general, to represent n (in decimal), we need k = lg n binary bits o Why? Use the above process as a guide -- we will repeatedly divide by 2 until we reach 0. (UIT 2201: Hardware(a)) Page 14 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Exercise: 1. In the previous worked example on converting decimal numbers to binary, at the end of all the dividing-by-two, we collect the digits by going backwards! Why? Hint: Try working this out yourself. Try going forward instead. What is the binary number you get. Convert it back to decimal and see what you will get. Use 6 and 4 as examples. 2. Exercise Algorithm Decimal-to-Binary on the following inputs. For each input, what is the output binary number and the value of k? (a) 8 (b) 13 (UIT 2201: Hardware(a)) Page 15 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Exercise: 1. In the previous worked example on converting decimal numbers to binary, at the end of all the dividing-by-two, we collect the digits by going backwards! Why? Hint: Try working this out yourself. Try going forward instead. What is the binary number you get. Convert it back to decimal and see what you will get. Use 6 and 4 as examples. 2. Exercise Algorithm Decimal-to-Binary on the following inputs. For each input, what is the output binary number and the value of k? (a) 8 (b) 13 (UIT 2201: Hardware(a)) Page 15 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Decimal to Binary (2) -- Algorithm: Decimal-to-Binary(n) Input: Decimal number (n)10 Output: Binary representation (n)10 = (bk-1 … bj … b 0)2 begin let j 0; let num n; while (num > 0) do b[j] num mod 2; // remainder num div 2; // divide by 2 j j + 1; endwhile (j < k) do // pad preceding b[j] 0; // bits with 0’s j j + 1; endwhile Output B = (b[k-1] b[k-2] … b[1] b[0]) end. (UIT 2201: Hardware(a)) Page 16 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Decimal to Binary (2) -- Algorithm: Decimal-to-Binary(n) Input: Decimal number (n)10 Output: Binary representation (n)10 = (bk-1 … bj … b 0)2 begin let j 0; let num n; while (num > 0) do b[j] num mod 2; // remainder num div 2; // divide by 2 j j + 1; endwhile (j < k) do // pad preceding b[j] 0; // bits with 0’s j j + 1; endwhile Output B = (b[k-1] b[k-2] … b[1] b[0]) end. (UIT 2201: Hardware(a)) Page 16 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Representation of Numeric Data v Representing integers o Decimal integers are converted to binary integers o Given k bits, the largest unsigned integer is 2 k - 1 u Given 5 bits, the largest is 25 -1 = 31 o Signed integers must also include the sign-bit (to indicate positive or negative) (UIT 2201: Hardware(a)) Page 17 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Representation of Numeric Data v Representing integers o Decimal integers are converted to binary integers o Given k bits, the largest unsigned integer is 2 k - 1 u Given 5 bits, the largest is 25 -1 = 31 o Signed integers must also include the sign-bit (to indicate positive or negative) (UIT 2201: Hardware(a)) Page 17 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Representation of Numeric Data… v Binary number representation – number of bits o with 1 bit, can represent 2 numbers; [0, 1] o 2 bits 4 numbers, [0. . 3]; u 00, 01, 10, 11 o 3 bits 8 numbers, [0. . 7]; u 000, 001, 010, 011, …, 110, 111 o 4 bits 16 numbers, [0. . 15]; u 0000, 0001, 0010, …, 1110, 1111 o … v With k bits 2 k numbers, [0. . 2 k-1] v Typical computers today work with o 16 or 32 bit numbers! (UIT 2201: Hardware(a)) Page 18 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Representation of Numeric Data… v Binary number representation – number of bits o with 1 bit, can represent 2 numbers; [0, 1] o 2 bits 4 numbers, [0. . 3]; u 00, 01, 10, 11 o 3 bits 8 numbers, [0. . 7]; u 000, 001, 010, 011, …, 110, 111 o 4 bits 16 numbers, [0. . 15]; u 0000, 0001, 0010, …, 1110, 1111 o … v With k bits 2 k numbers, [0. . 2 k-1] v Typical computers today work with o 16 or 32 bit numbers! (UIT 2201: Hardware(a)) Page 18 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Representation of Numeric Data… v Representing real numbers o Real numbers may be put into binary scientific notation: a x 2 b u Example: 101. 11 x 20 o Number then normalized so that first significant digit is immediately to the right of the binary point u Example: . 10111 x 23 o Mantissa and exponent then stored u they both need a sign-bit (positive/negative) (UIT 2201: Hardware(a)) Page 19 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Representation of Numeric Data… v Representing real numbers o Real numbers may be put into binary scientific notation: a x 2 b u Example: 101. 11 x 20 o Number then normalized so that first significant digit is immediately to the right of the binary point u Example: . 10111 x 23 o Mantissa and exponent then stored u they both need a sign-bit (positive/negative) (UIT 2201: Hardware(a)) Page 19 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Number Representations v Read up on o Signed magnitude numbers o “floating point” representation of real numbers u Mantissa, exponent v Readings: Section 4. ? of [SG] (UIT 2201: Hardware(a)) Page 20 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Number Representations v Read up on o Signed magnitude numbers o “floating point” representation of real numbers u Mantissa, exponent v Readings: Section 4. ? of [SG] (UIT 2201: Hardware(a)) Page 20 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Representation of Textual Information v Computers process numbers, but also textual information o non numeric data and text o 0 1 … 9 a b …z. | + * ( & o special control characters eg: CR, tabs v ASCII (American Standard Code for Information Interchange) “as-kee” o uses 7 bit code for each character o Usually, a 0 is added in front u “A” is 01000001 u “a” is 01100001 (UIT 2201: Hardware(a)) Page 21 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Representation of Textual Information v Computers process numbers, but also textual information o non numeric data and text o 0 1 … 9 a b …z. | + * ( & o special control characters eg: CR, tabs v ASCII (American Standard Code for Information Interchange) “as-kee” o uses 7 bit code for each character o Usually, a 0 is added in front u “A” is 01000001 u “a” is 01100001 (UIT 2201: Hardware(a)) Page 21 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Representation of Textual Information… v Characters are mapped into binary codes o ASCII code set (8 bits per character; 256 character codes) o UNICODE code set (16 bits, 65, 536 character codes) v For example: using ASCII codes, we can represent o numbers, letters (as characters) o Names of people, sentences u as sequences of characters “Hello World!” u The above contains 12 characters (without the quotes “”) v Represent instructions (eg: ADD, SUB) o we first assign them codes ADD 00 SUB 01 … … o and then represent the codes. . (UIT 2201: Hardware(a)) Page 22 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Representation of Textual Information… v Characters are mapped into binary codes o ASCII code set (8 bits per character; 256 character codes) o UNICODE code set (16 bits, 65, 536 character codes) v For example: using ASCII codes, we can represent o numbers, letters (as characters) o Names of people, sentences u as sequences of characters “Hello World!” u The above contains 12 characters (without the quotes “”) v Represent instructions (eg: ADD, SUB) o we first assign them codes ADD 00 SUB 01 … … o and then represent the codes. . (UIT 2201: Hardware(a)) Page 22 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Representation of Sound and Images v Multimedia data is sampled to store a digital form, with or without detectable differences v Representing sound data o Sound data must be digitized for storage in a computer o Digitizing means periodic sampling of amplitude values (UIT 2201: Hardware(a)) Page 23 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Representation of Sound and Images v Multimedia data is sampled to store a digital form, with or without detectable differences v Representing sound data o Sound data must be digitized for storage in a computer o Digitizing means periodic sampling of amplitude values (UIT 2201: Hardware(a)) Page 23 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
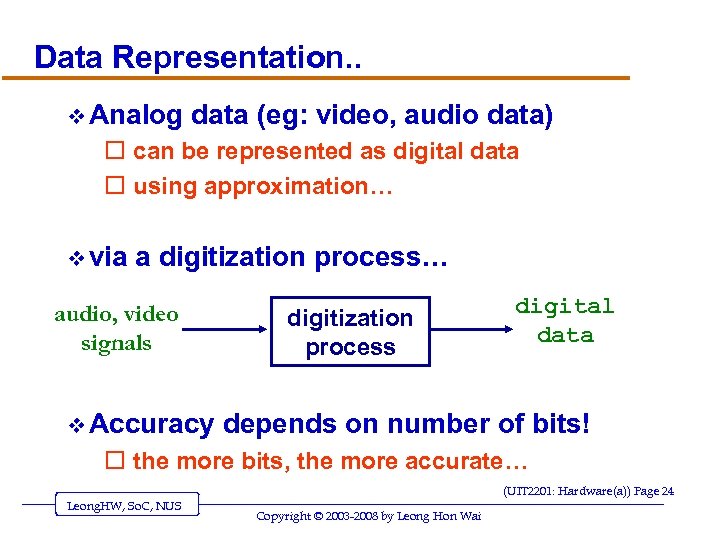 Data Representation. . v Analog data (eg: video, audio data) o can be represented as digital data o using approximation… v via a digitization process… audio, video signals v Accuracy digitization process digital data depends on number of bits! o the more bits, the more accurate… (UIT 2201: Hardware(a)) Page 24 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Data Representation. . v Analog data (eg: video, audio data) o can be represented as digital data o using approximation… v via a digitization process… audio, video signals v Accuracy digitization process digital data depends on number of bits! o the more bits, the more accurate… (UIT 2201: Hardware(a)) Page 24 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
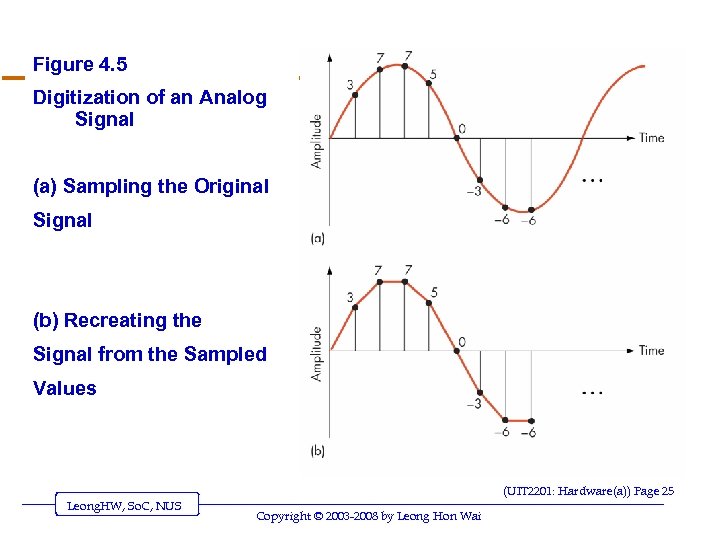 Figure 4. 5 Digitization of an Analog Signal (a) Sampling the Original Signal (b) Recreating the Signal from the Sampled Values (UIT 2201: Hardware(a)) Page 25 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 5 Digitization of an Analog Signal (a) Sampling the Original Signal (b) Recreating the Signal from the Sampled Values (UIT 2201: Hardware(a)) Page 25 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Data Representation – Analog Data? v What about analog data? o Why is analog data problematic? v How o o o o to represent (2. 1)10 in binary? (10. 1)2 = (2. 5)10 (10. 01)2 = (2. 25)10 (10. 001)2 = (2. 125)10 (10. 0001)2 = (2. 0625)10 (10. 00011)2 = (2. 09375)10 (10. 000111)2 = (2. 109375)10 …… v CANNOT represent (2. 1)10 exactly in binary!! o We can only give an approximation. o Accuracy depends on the number of bits (UIT 2201: Hardware(a)) Page 26 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Data Representation – Analog Data? v What about analog data? o Why is analog data problematic? v How o o o o to represent (2. 1)10 in binary? (10. 1)2 = (2. 5)10 (10. 01)2 = (2. 25)10 (10. 001)2 = (2. 125)10 (10. 0001)2 = (2. 0625)10 (10. 00011)2 = (2. 09375)10 (10. 000111)2 = (2. 109375)10 …… v CANNOT represent (2. 1)10 exactly in binary!! o We can only give an approximation. o Accuracy depends on the number of bits (UIT 2201: Hardware(a)) Page 26 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Representation of Sound (cont…) o From samples, original sound may be approximated o To improve the approximation: u Sample more frequently u Use more bits for each sample value (UIT 2201: Hardware(a)) Page 27 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Representation of Sound (cont…) o From samples, original sound may be approximated o To improve the approximation: u Sample more frequently u Use more bits for each sample value (UIT 2201: Hardware(a)) Page 27 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Representation of Images (cont. ) v Representing image data o Images are sampled by reading color and intensity values at even intervals across the image o Each sampled point is a pixel o Image quality depends on number of bits at each pixel (UIT 2201: Hardware(a)) Page 28 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Representation of Images (cont. ) v Representing image data o Images are sampled by reading color and intensity values at even intervals across the image o Each sampled point is a pixel o Image quality depends on number of bits at each pixel (UIT 2201: Hardware(a)) Page 28 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 The Reliability of Binary Representation v Electronic devices are most reliable in a bistable environment v Bistable environment o Distinguishing only two electronic states u Current flowing or not u Direction of flow v Computers are bistable: hence binary representations (UIT 2201: Hardware(a)) Page 29 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
The Reliability of Binary Representation v Electronic devices are most reliable in a bistable environment v Bistable environment o Distinguishing only two electronic states u Current flowing or not u Direction of flow v Computers are bistable: hence binary representations (UIT 2201: Hardware(a)) Page 29 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Storage Devices v Magnetic core o Historic device for computer memory o Tiny magnetized rings: flow of current sets the direction of magnetic field o Binary values 0 and 1 are represented using the direction of the magnetic field (UIT 2201: Hardware(a)) Page 30 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Storage Devices v Magnetic core o Historic device for computer memory o Tiny magnetized rings: flow of current sets the direction of magnetic field o Binary values 0 and 1 are represented using the direction of the magnetic field (UIT 2201: Hardware(a)) Page 30 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
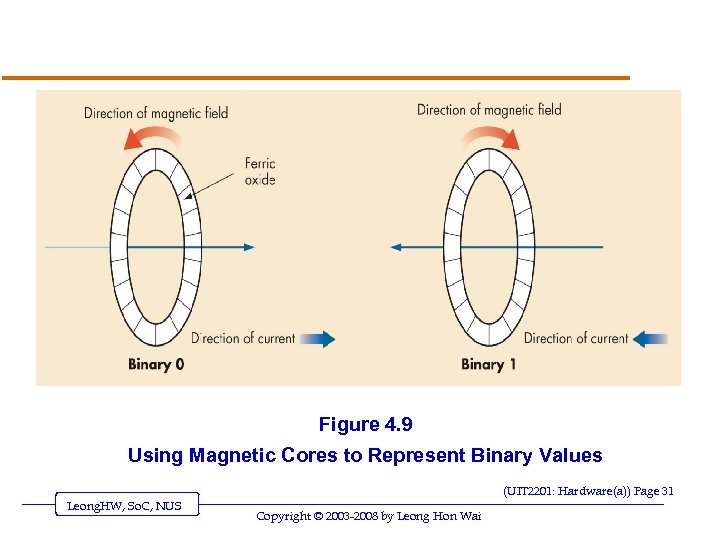 Figure 4. 9 Using Magnetic Cores to Represent Binary Values (UIT 2201: Hardware(a)) Page 31 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 9 Using Magnetic Cores to Represent Binary Values (UIT 2201: Hardware(a)) Page 31 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Binary Storage Devices (continued) v Transistors o Solid-state switches: either permits or blocks current flow o A control input causes state change o Constructed from semiconductors (UIT 2201: Hardware(a)) Page 32 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Binary Storage Devices (continued) v Transistors o Solid-state switches: either permits or blocks current flow o A control input causes state change o Constructed from semiconductors (UIT 2201: Hardware(a)) Page 32 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
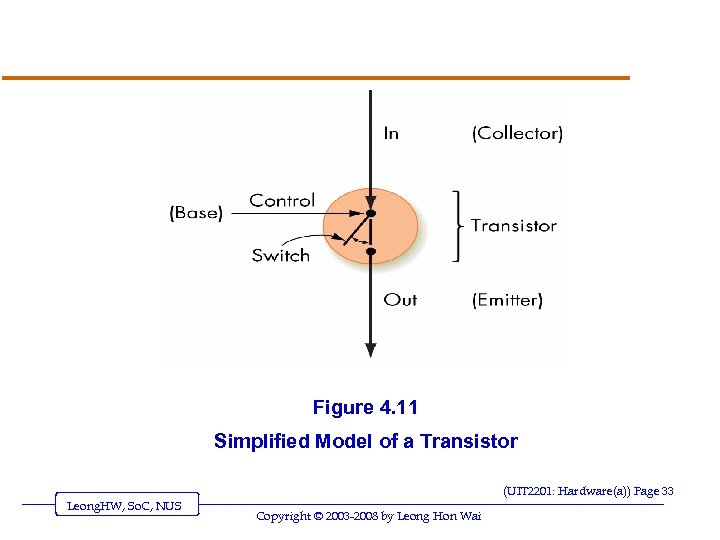 Figure 4. 11 Simplified Model of a Transistor (UIT 2201: Hardware(a)) Page 33 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 11 Simplified Model of a Transistor (UIT 2201: Hardware(a)) Page 33 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Hardware: The Basic Building Blocks 1. The Digital Computer 2. Binary Numbers 3. Boolean Logic and Basic Gates READING: Sect. 4. 3 to 4. 5 of [SG] & Notes 1. Boolean Logic 2. Basic Gates, Truth Tables 3. Simple Combinatorial Circuits 4. Simplification with Boolean Logic 4. Basic Circuit Design (UIT 2201: Hardware(a)) Page 34 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Hardware: The Basic Building Blocks 1. The Digital Computer 2. Binary Numbers 3. Boolean Logic and Basic Gates READING: Sect. 4. 3 to 4. 5 of [SG] & Notes 1. Boolean Logic 2. Basic Gates, Truth Tables 3. Simple Combinatorial Circuits 4. Simplification with Boolean Logic 4. Basic Circuit Design (UIT 2201: Hardware(a)) Page 34 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Boolean Logic and Gates: Boolean Logic v Boolean logic describes operations on true/false values v True/false maps easily onto bi-stable environment v Boolean logic operations on electronic signals may be built out of transistors and other electronic devices (UIT 2201: Hardware(a)) Page 35 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Boolean Logic and Gates: Boolean Logic v Boolean logic describes operations on true/false values v True/false maps easily onto bi-stable environment v Boolean logic operations on electronic signals may be built out of transistors and other electronic devices (UIT 2201: Hardware(a)) Page 35 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Boolean Circuits v Computer operations based on logic circuits o Logic based on Boolean Algebra v Logic circuits have o inputs (each with value 0 or 1) T/F o outputs o state v Type of Logic Circuits: o Combinational circuits: output depends only on input o Sequential circuits: output depends also on past history (get sequence of output…) v GATES: Basic Building Blocks for Circuits (UIT 2201: Hardware(a)) Page 36 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Boolean Circuits v Computer operations based on logic circuits o Logic based on Boolean Algebra v Logic circuits have o inputs (each with value 0 or 1) T/F o outputs o state v Type of Logic Circuits: o Combinational circuits: output depends only on input o Sequential circuits: output depends also on past history (get sequence of output…) v GATES: Basic Building Blocks for Circuits (UIT 2201: Hardware(a)) Page 36 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
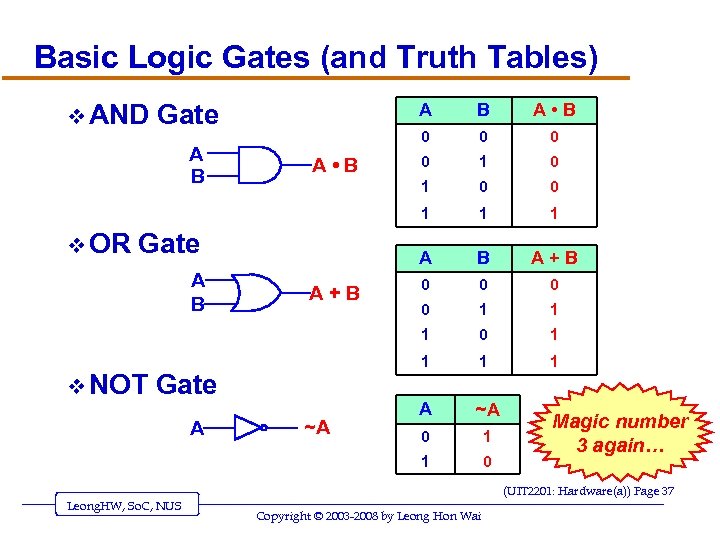 Basic Logic Gates (and Truth Tables) v AND Gate v NOT A ~A 0 0 0 1 1 B A+B 0 0 1 1 Gate 1 A A+B 0 1 1 A ~A 0 1 1 A B 0 1 Gate 0 1 v OR A • B 0 A • B B 1 A B A 0 Magic number 3 again… (UIT 2201: Hardware(a)) Page 37 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Basic Logic Gates (and Truth Tables) v AND Gate v NOT A ~A 0 0 0 1 1 B A+B 0 0 1 1 Gate 1 A A+B 0 1 1 A ~A 0 1 1 A B 0 1 Gate 0 1 v OR A • B 0 A • B B 1 A B A 0 Magic number 3 again… (UIT 2201: Hardware(a)) Page 37 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Gates v Gates are hardware devices built from transistors to “implement” Boolean logic v AND gate o Two input lines, one output line o Outputs a 1 when both inputs are 1 v OR gate o Two input lines, one output line o Outputs a 1 when either input is 1 v NOT gate o One input lines, one output line o Outputs a 1 when input is 0, and vice versa (UIT 2201: Hardware(a)) Page 38 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Gates v Gates are hardware devices built from transistors to “implement” Boolean logic v AND gate o Two input lines, one output line o Outputs a 1 when both inputs are 1 v OR gate o Two input lines, one output line o Outputs a 1 when either input is 1 v NOT gate o One input lines, one output line o Outputs a 1 when input is 0, and vice versa (UIT 2201: Hardware(a)) Page 38 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
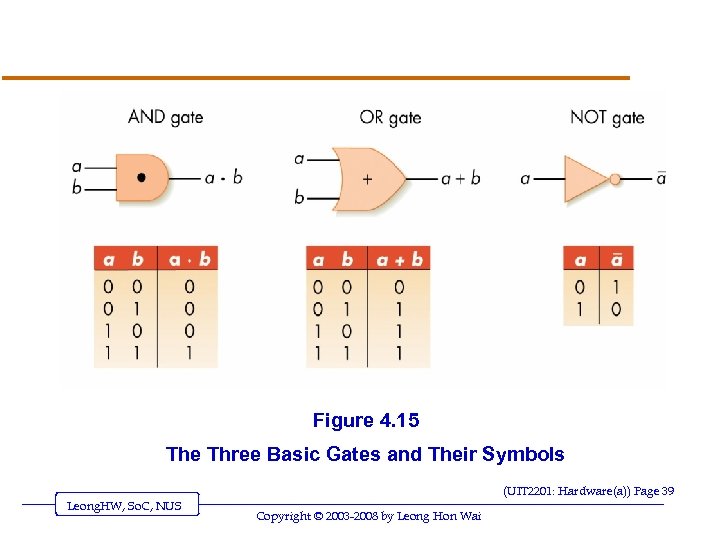 Figure 4. 15 The Three Basic Gates and Their Symbols (UIT 2201: Hardware(a)) Page 39 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 15 The Three Basic Gates and Their Symbols (UIT 2201: Hardware(a)) Page 39 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 What’s inside a Gate? v Gate made of physical components o called transistors o A transistor is formed by sandwiching a p-type silicon between two n-type silicon or vice versa. v In this course, we do not need to deal with the details of what’s inside a Gate. (UIT 2201: Hardware(a)) Page 40 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
What’s inside a Gate? v Gate made of physical components o called transistors o A transistor is formed by sandwiching a p-type silicon between two n-type silicon or vice versa. v In this course, we do not need to deal with the details of what’s inside a Gate. (UIT 2201: Hardware(a)) Page 40 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Gates (continued) v Abstraction in hardware design o Map hardware devices to Boolean logic o Design more complex devices in terms of logic, not electronics o Conversion from logic to hardware design may be automated (UIT 2201: Hardware(a)) Page 41 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Gates (continued) v Abstraction in hardware design o Map hardware devices to Boolean logic o Design more complex devices in terms of logic, not electronics o Conversion from logic to hardware design may be automated (UIT 2201: Hardware(a)) Page 41 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
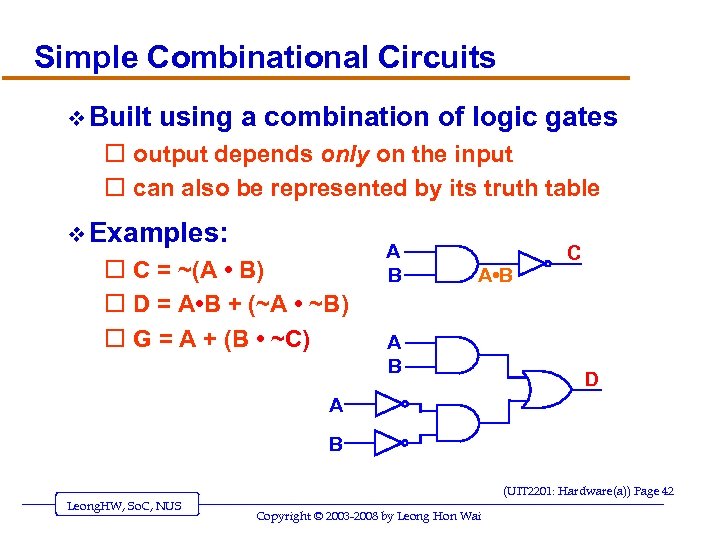 Simple Combinational Circuits v Built using a combination of logic gates o output depends only on the input o can also be represented by its truth table v Examples: o C = ~(A • B) o D = A • B + (~A • ~B) o G = A + (B • ~C) A B A • B A B C D A B (UIT 2201: Hardware(a)) Page 42 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Simple Combinational Circuits v Built using a combination of logic gates o output depends only on the input o can also be represented by its truth table v Examples: o C = ~(A • B) o D = A • B + (~A • ~B) o G = A + (B • ~C) A B A • B A B C D A B (UIT 2201: Hardware(a)) Page 42 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
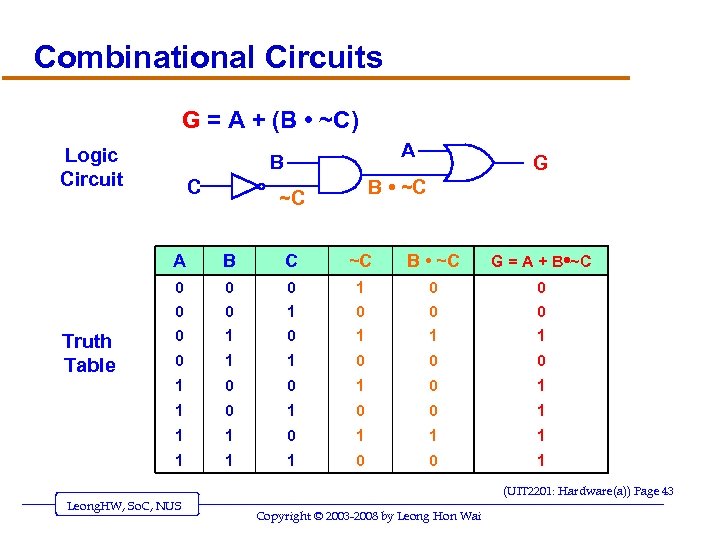 Combinational Circuits G = A + (B • ~C) Logic Circuit A B C G B • ~C ~C A C ~C B • ~C G = A + B • ~C 0 0 0 1 0 0 0 0 1 1 1 0 0 0 1 0 1 1 0 0 1 1 1 1 Truth Table B 1 1 0 0 1 (UIT 2201: Hardware(a)) Page 43 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Combinational Circuits G = A + (B • ~C) Logic Circuit A B C G B • ~C ~C A C ~C B • ~C G = A + B • ~C 0 0 0 1 0 0 0 0 1 1 1 0 0 0 1 0 1 1 0 0 1 1 1 1 Truth Table B 1 1 0 0 1 (UIT 2201: Hardware(a)) Page 43 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Logic Circuits: An aside… v Possible Interpretation of G “Sound the buzzer if 1. temperature of engine exceeds 200°F, or 2. car is in gear and driver’s seat-belt is not buckled” o We define… u G: “Sound buzzer” u A: “Temperature of engine exceeds 200°F” u B: “Car is in gear” u C: “driver’s seat-belt is buckled” o G = A + (B • ~C) v HW: Give other interpretations… (UIT 2201: Hardware(a)) Page 44 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Logic Circuits: An aside… v Possible Interpretation of G “Sound the buzzer if 1. temperature of engine exceeds 200°F, or 2. car is in gear and driver’s seat-belt is not buckled” o We define… u G: “Sound buzzer” u A: “Temperature of engine exceeds 200°F” u B: “Car is in gear” u C: “driver’s seat-belt is buckled” o G = A + (B • ~C) v HW: Give other interpretations… (UIT 2201: Hardware(a)) Page 44 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Manipulation with Logical Expressions v Can manipulate / simplify logical expression o subject to Algebraic Laws (Boolean algebra) v Examples: o Commutative Laws u (A + B) = (B + A) u. A • B = B • A (Note: shorthand A • B as AB) o Associative Laws u A + (B + C) = (A + B) + C u A • (B • C) = (A • B) • C o Distributive Laws u A • (B + C) = (A • B) + (A • C) u A + (B • C) = (A+B) • (A+C) Complementary Law: Given any boolean law, change all “+” to “ • ”, and change all “ • ” to “+”, and change all “ 1” to “ 0” and change all “ 0” to “ 1” to get the complementary law. (UIT 2201: Hardware(a)) Page 45 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Manipulation with Logical Expressions v Can manipulate / simplify logical expression o subject to Algebraic Laws (Boolean algebra) v Examples: o Commutative Laws u (A + B) = (B + A) u. A • B = B • A (Note: shorthand A • B as AB) o Associative Laws u A + (B + C) = (A + B) + C u A • (B • C) = (A • B) • C o Distributive Laws u A • (B + C) = (A • B) + (A • C) u A + (B • C) = (A+B) • (A+C) Complementary Law: Given any boolean law, change all “+” to “ • ”, and change all “ • ” to “+”, and change all “ 1” to “ 0” and change all “ 0” to “ 1” to get the complementary law. (UIT 2201: Hardware(a)) Page 45 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
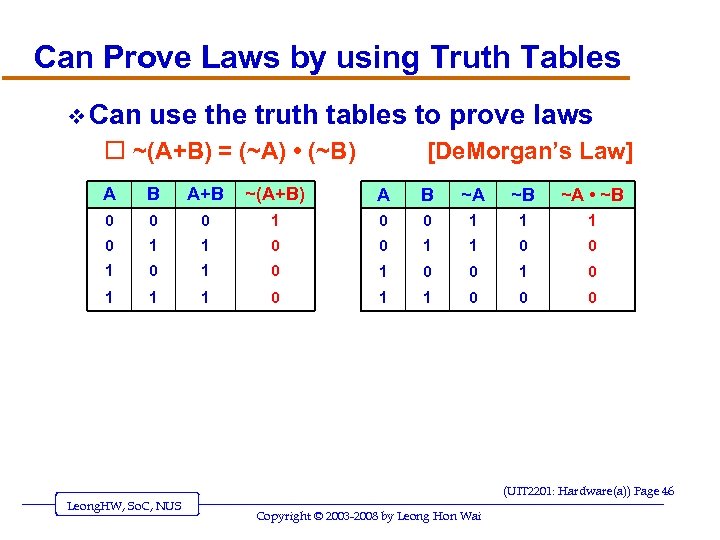 Can Prove Laws by using Truth Tables v Can use the truth tables to prove laws o ~(A+B) = (~A) • (~B) [De. Morgan’s Law] A B A+B ~(A+B) A B ~A ~B ~A • ~B 0 0 0 1 1 1 0 0 1 0 1 0 1 1 1 0 0 0 (UIT 2201: Hardware(a)) Page 46 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Can Prove Laws by using Truth Tables v Can use the truth tables to prove laws o ~(A+B) = (~A) • (~B) [De. Morgan’s Law] A B A+B ~(A+B) A B ~A ~B ~A • ~B 0 0 0 1 1 1 0 0 1 0 1 0 1 1 1 0 0 0 (UIT 2201: Hardware(a)) Page 46 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 HW: Prove the following laws… v Using o o o o o Truth tables or otherwise, prove ~(A • B) = ~A + ~B [De. Morgan’s Law] ~(A + B) = ~A • ~B [De. Morgan’s Law] A • (B + C) = (A • B) + (A • C) [Distributive Law] A + (B • C) = (A+B) • (A+C) [Distributive Law] A+A • B=A [Absorption Law] A • (A + B) = A [Absorption Law] A + ~A = 1; A • ~A = 0; A • 1 = A; A + 0 = A; Use these laws to A • 0 = 0; A + 1 = 1; simplify your circuits. (UIT 2201: Hardware(a)) Page 47 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
HW: Prove the following laws… v Using o o o o o Truth tables or otherwise, prove ~(A • B) = ~A + ~B [De. Morgan’s Law] ~(A + B) = ~A • ~B [De. Morgan’s Law] A • (B + C) = (A • B) + (A • C) [Distributive Law] A + (B • C) = (A+B) • (A+C) [Distributive Law] A+A • B=A [Absorption Law] A • (A + B) = A [Absorption Law] A + ~A = 1; A • ~A = 0; A • 1 = A; A + 0 = A; Use these laws to A • 0 = 0; A + 1 = 1; simplify your circuits. (UIT 2201: Hardware(a)) Page 47 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 More Basic Logic Gates v XOR Gate A NAND B 0 1 1 1 0 B NAND 0 0 1 1 B A 0 A Gate 0 1 v NAND XOR 0 A B B 1 A B A 1 0 Question: How many types of basic logic gates do we really need? (UIT 2201: Hardware(a)) Page 48 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
More Basic Logic Gates v XOR Gate A NAND B 0 1 1 1 0 B NAND 0 0 1 1 B A 0 A Gate 0 1 v NAND XOR 0 A B B 1 A B A 1 0 Question: How many types of basic logic gates do we really need? (UIT 2201: Hardware(a)) Page 48 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Logical Completeness v{ +, • , ~ } is logically complete v{ • , ~ } is logically complete (p + q) = ~( (~p) • (~q) ) v{ +, ~ } is logically complete v{ +, • } is NOT logically complete v{ NAND } is logically complete (p NAND p) = (~p) (~p NAND ~q) = (p + q) (UIT 2201: Hardware(a)) Page 49 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Logical Completeness v{ +, • , ~ } is logically complete v{ • , ~ } is logically complete (p + q) = ~( (~p) • (~q) ) v{ +, ~ } is logically complete v{ +, • } is NOT logically complete v{ NAND } is logically complete (p NAND p) = (~p) (~p NAND ~q) = (p + q) (UIT 2201: Hardware(a)) Page 49 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
![Building Computer Circuits: Introduction v Read v. A [SG 3]-Ch. 4. 4. 2 CAREFULLY. Building Computer Circuits: Introduction v Read v. A [SG 3]-Ch. 4. 4. 2 CAREFULLY.](https://present5.com/presentation/d8ec9a105f65d73cea7e10f4bf3b025c/image-50.jpg) Building Computer Circuits: Introduction v Read v. A [SG 3]-Ch. 4. 4. 2 CAREFULLY. circuit is a collection of logic gates: o Transforms a set of binary inputs into a set of binary outputs o Values of the outputs depend only on the current values of the inputs v Combinational circuits have no cycles in them (no outputs feed back into their own inputs) (UIT 2201: Hardware(a)) Page 50 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Building Computer Circuits: Introduction v Read v. A [SG 3]-Ch. 4. 4. 2 CAREFULLY. circuit is a collection of logic gates: o Transforms a set of binary inputs into a set of binary outputs o Values of the outputs depend only on the current values of the inputs v Combinational circuits have no cycles in them (no outputs feed back into their own inputs) (UIT 2201: Hardware(a)) Page 50 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
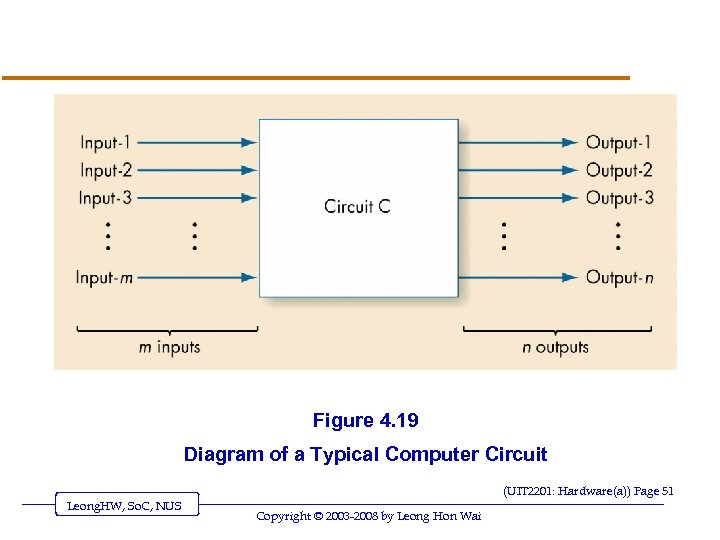 Figure 4. 19 Diagram of a Typical Computer Circuit (UIT 2201: Hardware(a)) Page 51 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 19 Diagram of a Typical Computer Circuit (UIT 2201: Hardware(a)) Page 51 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 A Circuit Construction Algorithm v Truth Table Boolean Expression Logic Circuits Fig. 4. 21: The Sum-of-Products Circuit Construction Algorithm (UIT 2201: Hardware(a)) Page 52 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
A Circuit Construction Algorithm v Truth Table Boolean Expression Logic Circuits Fig. 4. 21: The Sum-of-Products Circuit Construction Algorithm (UIT 2201: Hardware(a)) Page 52 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 A Circuit Construction Algorithm (cont…) v Sum-of-products algorithm o Truth table captures every input/output possible for circuit o Repeat process for each output line u Build a Boolean expression using AND and NOT for each 1 of the output line u Combine together all the expressions with ORs u Build circuit from whole Boolean expression (UIT 2201: Hardware(a)) Page 53 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
A Circuit Construction Algorithm (cont…) v Sum-of-products algorithm o Truth table captures every input/output possible for circuit o Repeat process for each output line u Build a Boolean expression using AND and NOT for each 1 of the output line u Combine together all the expressions with ORs u Build circuit from whole Boolean expression (UIT 2201: Hardware(a)) Page 53 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
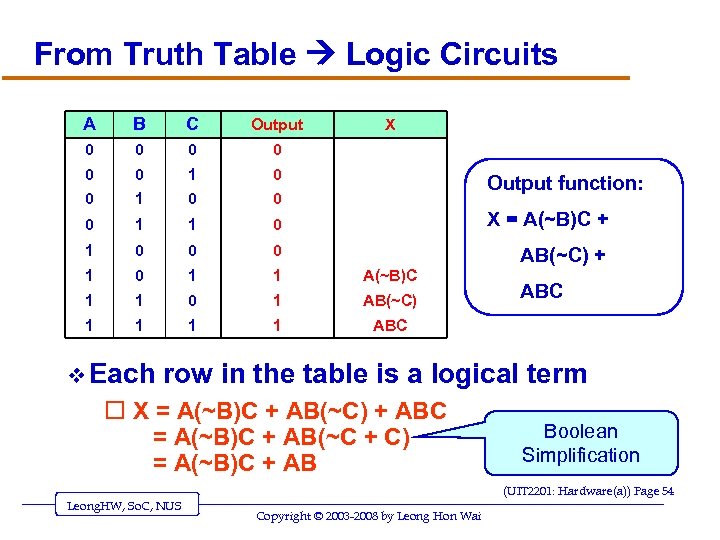 From Truth Table Logic Circuits A B C Output 0 0 0 1 1 0 X = A(~B)C + 1 0 0 0 AB(~C) + 1 0 1 1 A(~B)C 1 1 0 1 AB(~C) 1 1 ABC v Each X Output function: ABC row in the table is a logical term o X = A(~B)C + AB(~C) + ABC = A(~B)C + AB(~C + C) = A(~B)C + AB Boolean Simplification (UIT 2201: Hardware(a)) Page 54 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
From Truth Table Logic Circuits A B C Output 0 0 0 1 1 0 X = A(~B)C + 1 0 0 0 AB(~C) + 1 0 1 1 A(~B)C 1 1 0 1 AB(~C) 1 1 ABC v Each X Output function: ABC row in the table is a logical term o X = A(~B)C + AB(~C) + ABC = A(~B)C + AB(~C + C) = A(~B)C + AB Boolean Simplification (UIT 2201: Hardware(a)) Page 54 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
![Examples of Circuit Design And Construction v Read v Two [SG 3]-Ch. 4. 4. Examples of Circuit Design And Construction v Read v Two [SG 3]-Ch. 4. 4.](https://present5.com/presentation/d8ec9a105f65d73cea7e10f4bf3b025c/image-55.jpg) Examples of Circuit Design And Construction v Read v Two [SG 3]-Ch. 4. 4. 3 examples: o Compare-for-equality circuit (comparator) o Addition circuit (adder) v REMARKS: Both circuits can be built using the sum-of-products algorithm (UIT 2201: Hardware(a)) Page 55 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Examples of Circuit Design And Construction v Read v Two [SG 3]-Ch. 4. 4. 3 examples: o Compare-for-equality circuit (comparator) o Addition circuit (adder) v REMARKS: Both circuits can be built using the sum-of-products algorithm (UIT 2201: Hardware(a)) Page 55 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
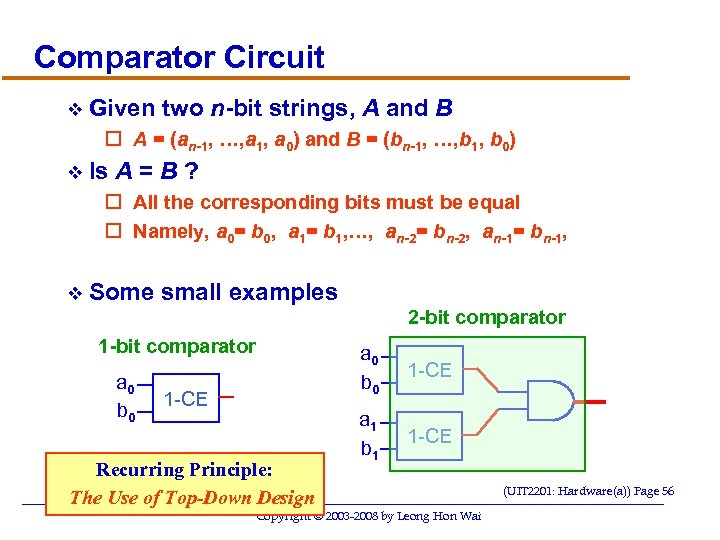 Comparator Circuit v Given two n-bit strings, A and B o A = (an-1, …, a 1, a 0) and B = (bn-1, …, b 1, b 0) v Is A=B? o All the corresponding bits must be equal o Namely, a 0= b 0, a 1= b 1, …, an-2= bn-2, an-1= bn-1, v Some small examples 2 -bit comparator 1 -bit comparator a 0 b 0 1 -CE Recurring Principle: The Use of Top-Down Design Leong. HW, So. C, NUS a 0 b 0 1 -CE a 1 b 1 1 -CE Copyright © 2003 -2008 by Leong Hon Wai (UIT 2201: Hardware(a)) Page 56
Comparator Circuit v Given two n-bit strings, A and B o A = (an-1, …, a 1, a 0) and B = (bn-1, …, b 1, b 0) v Is A=B? o All the corresponding bits must be equal o Namely, a 0= b 0, a 1= b 1, …, an-2= bn-2, an-1= bn-1, v Some small examples 2 -bit comparator 1 -bit comparator a 0 b 0 1 -CE Recurring Principle: The Use of Top-Down Design Leong. HW, So. C, NUS a 0 b 0 1 -CE a 1 b 1 1 -CE Copyright © 2003 -2008 by Leong Hon Wai (UIT 2201: Hardware(a)) Page 56
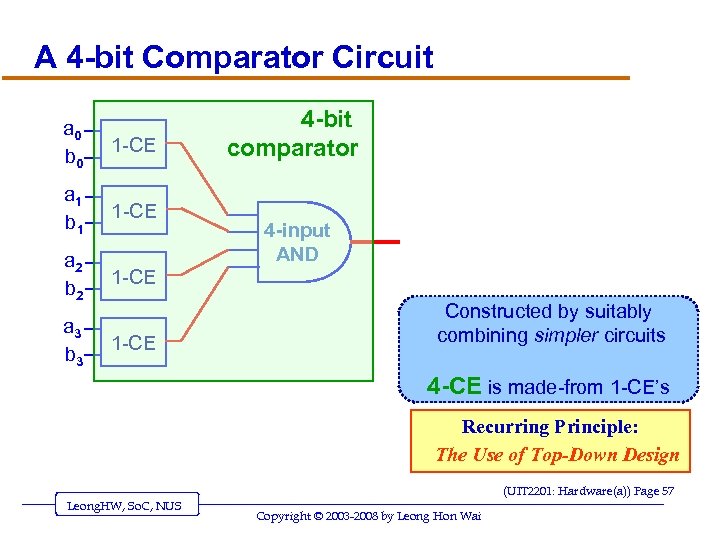 A 4 -bit Comparator Circuit a 0 b 0 1 -CE a 1 b 1 1 -CE a 2 b 2 1 -CE a 3 b 3 1 -CE 4 -bit comparator 4 -input AND Constructed by suitably combining simpler circuits 4 -CE is made-from 1 -CE’s Recurring Principle: The Use of Top-Down Design (UIT 2201: Hardware(a)) Page 57 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
A 4 -bit Comparator Circuit a 0 b 0 1 -CE a 1 b 1 1 -CE a 2 b 2 1 -CE a 3 b 3 1 -CE 4 -bit comparator 4 -input AND Constructed by suitably combining simpler circuits 4 -CE is made-from 1 -CE’s Recurring Principle: The Use of Top-Down Design (UIT 2201: Hardware(a)) Page 57 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
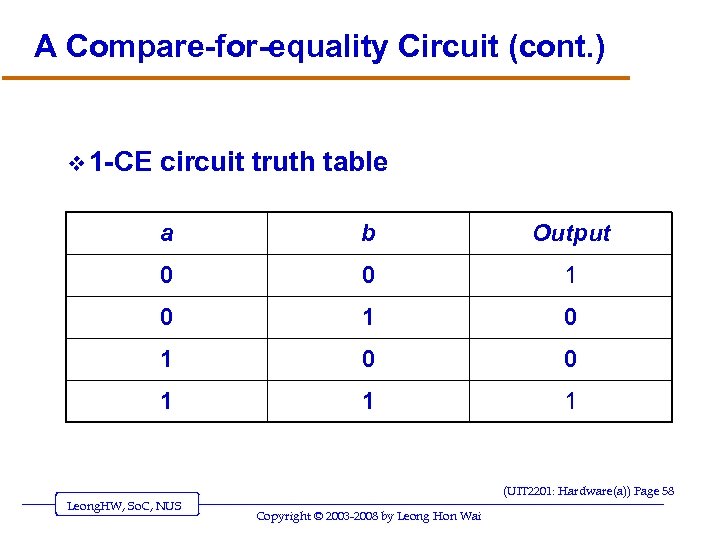 A Compare-for-equality Circuit (cont. ) v 1 -CE circuit truth table a b Output 0 0 1 0 1 0 0 1 1 1 (UIT 2201: Hardware(a)) Page 58 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
A Compare-for-equality Circuit (cont. ) v 1 -CE circuit truth table a b Output 0 0 1 0 1 0 0 1 1 1 (UIT 2201: Hardware(a)) Page 58 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 A Compare-for-equality Circuit (cont…) v 1 -CE Boolean expression o First case: (~a) * (~b) o Second case: a * b o Combined: (a*b) + (~a * ~b) (UIT 2201: Hardware(a)) Page 59 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
A Compare-for-equality Circuit (cont…) v 1 -CE Boolean expression o First case: (~a) * (~b) o Second case: a * b o Combined: (a*b) + (~a * ~b) (UIT 2201: Hardware(a)) Page 59 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
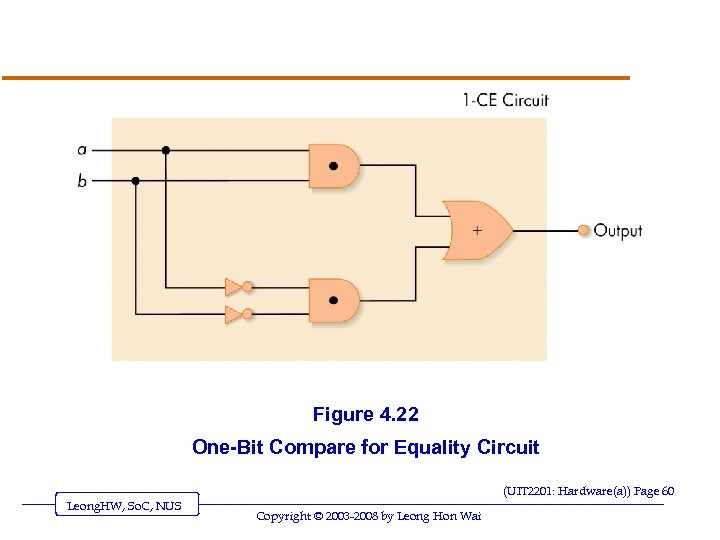 Figure 4. 22 One-Bit Compare for Equality Circuit (UIT 2201: Hardware(a)) Page 60 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 22 One-Bit Compare for Equality Circuit (UIT 2201: Hardware(a)) Page 60 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Adding two Binary Numbers… v Similar to those for decimal # (simpler) o Actually, use the same algorithm! v To o o add two bits, we have 0+0=0 0+1=1 1+0=1 1 + 1 = 0 (with carry 1) v What about adding three bits? v Adding two binary numbers: (do it yourself) 101101100 11010 (UIT 2201: Hardware(a)) Page 61 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Adding two Binary Numbers… v Similar to those for decimal # (simpler) o Actually, use the same algorithm! v To o o add two bits, we have 0+0=0 0+1=1 1+0=1 1 + 1 = 0 (with carry 1) v What about adding three bits? v Adding two binary numbers: (do it yourself) 101101100 11010 (UIT 2201: Hardware(a)) Page 61 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 An Addition Circuit v Addition circuit o Adds two unsigned binary integers, setting output bits and an overflow o Built from 1 -bit adders (1 -ADD) o Starting with rightmost bits, each pair produces u A value for the output sum-bit u A carry bit for next place to the left (UIT 2201: Hardware(a)) Page 62 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
An Addition Circuit v Addition circuit o Adds two unsigned binary integers, setting output bits and an overflow o Built from 1 -bit adders (1 -ADD) o Starting with rightmost bits, each pair produces u A value for the output sum-bit u A carry bit for next place to the left (UIT 2201: Hardware(a)) Page 62 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 An Addition Circuit (continued) v 1 -ADD truth table o Input u One bit from each input integer u One carry bit (always zero for rightmost bit) o Output u One bit for output place value u One “carry” bit (UIT 2201: Hardware(a)) Page 63 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
An Addition Circuit (continued) v 1 -ADD truth table o Input u One bit from each input integer u One carry bit (always zero for rightmost bit) o Output u One bit for output place value u One “carry” bit (UIT 2201: Hardware(a)) Page 63 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
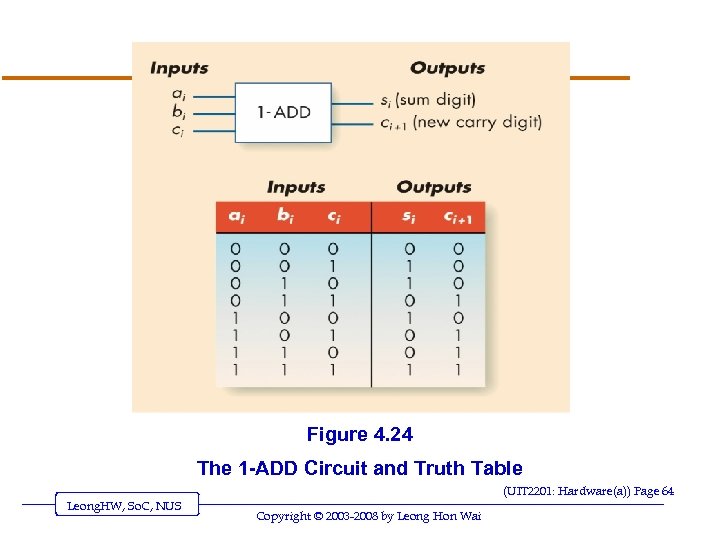 Figure 4. 24 The 1 -ADD Circuit and Truth Table (UIT 2201: Hardware(a)) Page 64 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 24 The 1 -ADD Circuit and Truth Table (UIT 2201: Hardware(a)) Page 64 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
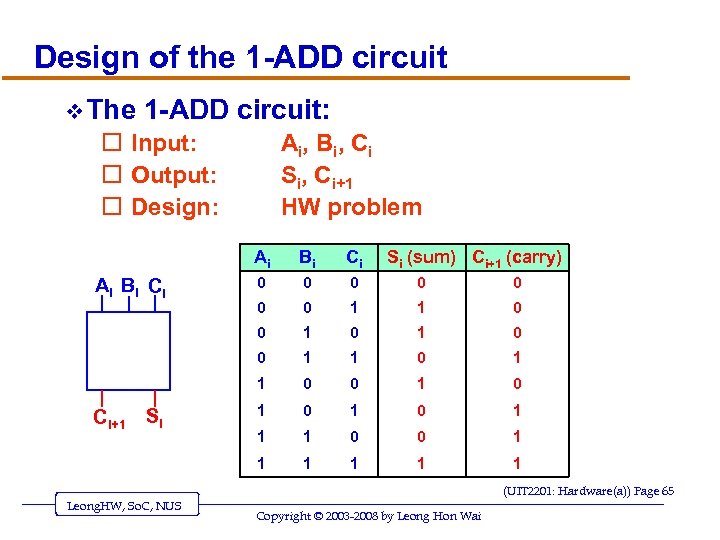 Design of the 1 -ADD circuit v The 1 -ADD circuit: o Input: o Output: o Design: Ai , B i , Ci Si, Ci+1 HW problem Ai 0 0 0 0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 1 Ci+1 Si Ci 0 Ai Bi Ci Bi Si (sum) Ci+1 (carry) 1 1 (UIT 2201: Hardware(a)) Page 65 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Design of the 1 -ADD circuit v The 1 -ADD circuit: o Input: o Output: o Design: Ai , B i , Ci Si, Ci+1 HW problem Ai 0 0 0 0 1 1 0 1 0 0 1 0 1 1 1 0 0 1 1 Ci+1 Si Ci 0 Ai Bi Ci Bi Si (sum) Ci+1 (carry) 1 1 (UIT 2201: Hardware(a)) Page 65 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 An Addition Circuit (continued) v Building the full adder o Put rightmost bits into 1 -ADD, with zero for the input carry o Send 1 -ADD’s output value to output, and put its carry value as input to 1 -ADD for next bits to left o Repeat process for all bits (UIT 2201: Hardware(a)) Page 66 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
An Addition Circuit (continued) v Building the full adder o Put rightmost bits into 1 -ADD, with zero for the input carry o Send 1 -ADD’s output value to output, and put its carry value as input to 1 -ADD for next bits to left o Repeat process for all bits (UIT 2201: Hardware(a)) Page 66 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
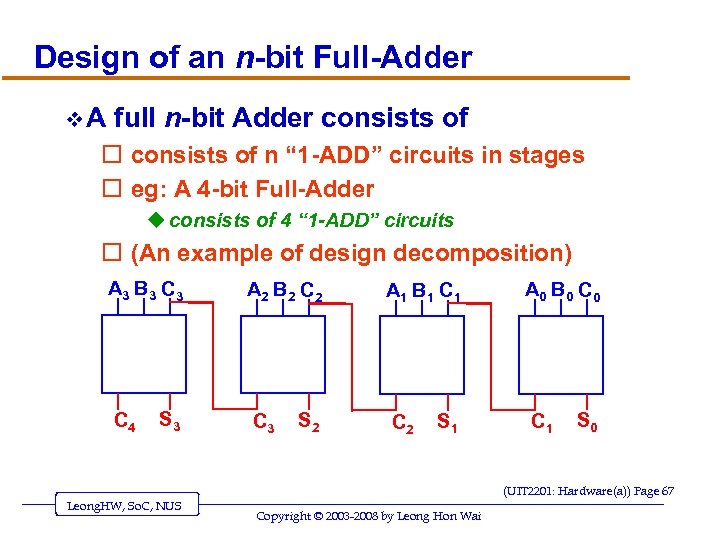 Design of an n-bit Full-Adder v. A full n-bit Adder consists of o consists of n “ 1 -ADD” circuits in stages o eg: A 4 -bit Full-Adder u consists of 4 “ 1 -ADD” circuits o (An example of design decomposition) A 3 B 3 C 4 S 3 A 2 B 2 C 3 S 2 A 1 B 1 C 2 S 1 A 0 B 0 C 1 S 0 (UIT 2201: Hardware(a)) Page 67 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Design of an n-bit Full-Adder v. A full n-bit Adder consists of o consists of n “ 1 -ADD” circuits in stages o eg: A 4 -bit Full-Adder u consists of 4 “ 1 -ADD” circuits o (An example of design decomposition) A 3 B 3 C 4 S 3 A 2 B 2 C 3 S 2 A 1 B 1 C 2 S 1 A 0 B 0 C 1 S 0 (UIT 2201: Hardware(a)) Page 67 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Control Circuits v Do not perform computations v Choose order of operations or select among data values v Major types of controls circuits o Multiplexors u Select one of inputs to send to output o Decoders u Sends a 1 on one output line, based on what input line indicates (UIT 2201: Hardware(a)) Page 68 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Control Circuits v Do not perform computations v Choose order of operations or select among data values v Major types of controls circuits o Multiplexors u Select one of inputs to send to output o Decoders u Sends a 1 on one output line, based on what input line indicates (UIT 2201: Hardware(a)) Page 68 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Control Circuits (continued) v Multiplexor form o 2 N regular input lines o N selector input lines o 1 output line v Multiplexor purpose o Given a code number for some input, selects that input to pass along to its output o Used to choose the right input value to send to a computational circuit (UIT 2201: Hardware(a)) Page 69 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Control Circuits (continued) v Multiplexor form o 2 N regular input lines o N selector input lines o 1 output line v Multiplexor purpose o Given a code number for some input, selects that input to pass along to its output o Used to choose the right input value to send to a computational circuit (UIT 2201: Hardware(a)) Page 69 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
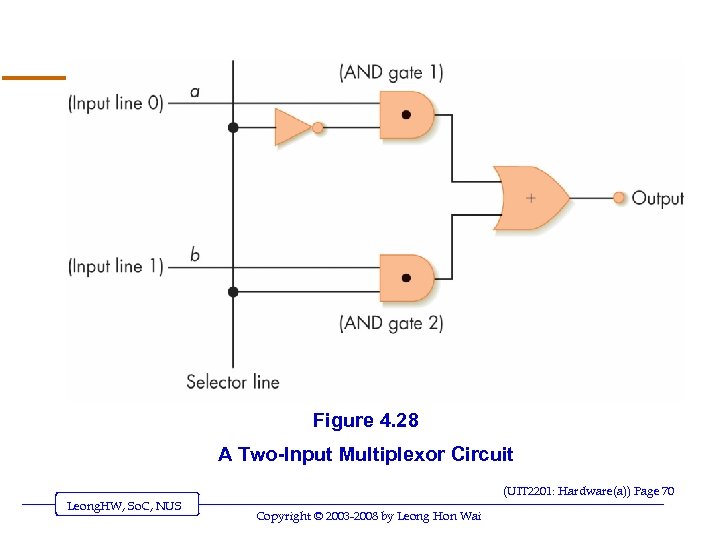 Figure 4. 28 A Two-Input Multiplexor Circuit (UIT 2201: Hardware(a)) Page 70 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 28 A Two-Input Multiplexor Circuit (UIT 2201: Hardware(a)) Page 70 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Control Circuits (continued) v Decoder o Form u N input lines u 2 N output lines o N input lines indicate a binary number, which is used to select one of the output lines o Selected output sends a 1, all others send 0 (UIT 2201: Hardware(a)) Page 71 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Control Circuits (continued) v Decoder o Form u N input lines u 2 N output lines o N input lines indicate a binary number, which is used to select one of the output lines o Selected output sends a 1, all others send 0 (UIT 2201: Hardware(a)) Page 71 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Control Circuits (continued) v Decoder purpose o Given a number code for some operation, trigger just that operation to take place o Numbers might be codes for arithmetic: add, subtract, etc. o Decoder signals which operation takes place next (UIT 2201: Hardware(a)) Page 72 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Control Circuits (continued) v Decoder purpose o Given a number code for some operation, trigger just that operation to take place o Numbers might be codes for arithmetic: add, subtract, etc. o Decoder signals which operation takes place next (UIT 2201: Hardware(a)) Page 72 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
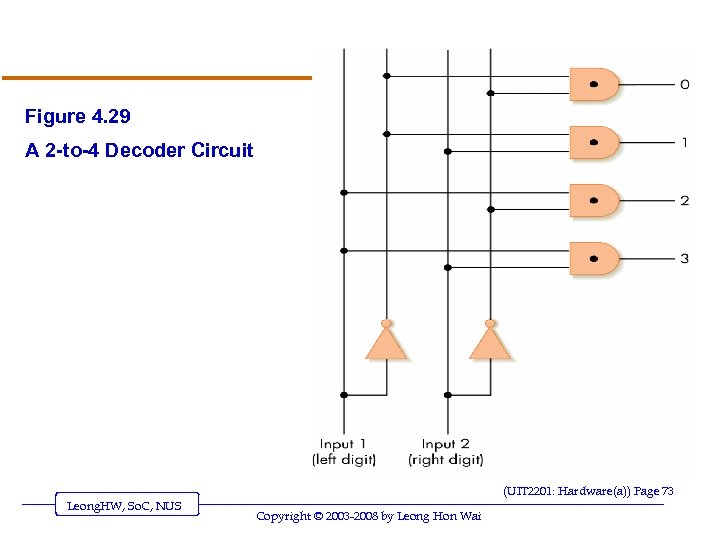 Figure 4. 29 A 2 -to-4 Decoder Circuit (UIT 2201: Hardware(a)) Page 73 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Figure 4. 29 A 2 -to-4 Decoder Circuit (UIT 2201: Hardware(a)) Page 73 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
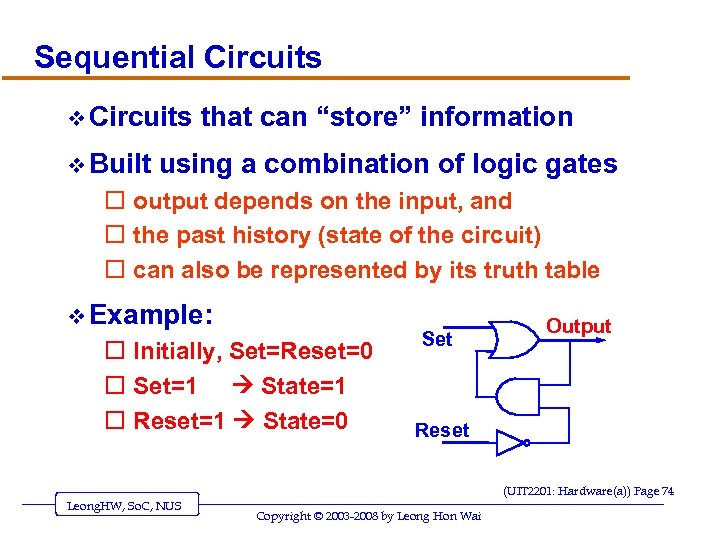 Sequential Circuits v Built that can “store” information using a combination of logic gates o output depends on the input, and o the past history (state of the circuit) o can also be represented by its truth table v Example: o Initially, Set=Reset=0 o Set=1 State=1 o Reset=1 State=0 Set Output Reset (UIT 2201: Hardware(a)) Page 74 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Sequential Circuits v Built that can “store” information using a combination of logic gates o output depends on the input, and o the past history (state of the circuit) o can also be represented by its truth table v Example: o Initially, Set=Reset=0 o Set=1 State=1 o Reset=1 State=0 Set Output Reset (UIT 2201: Hardware(a)) Page 74 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
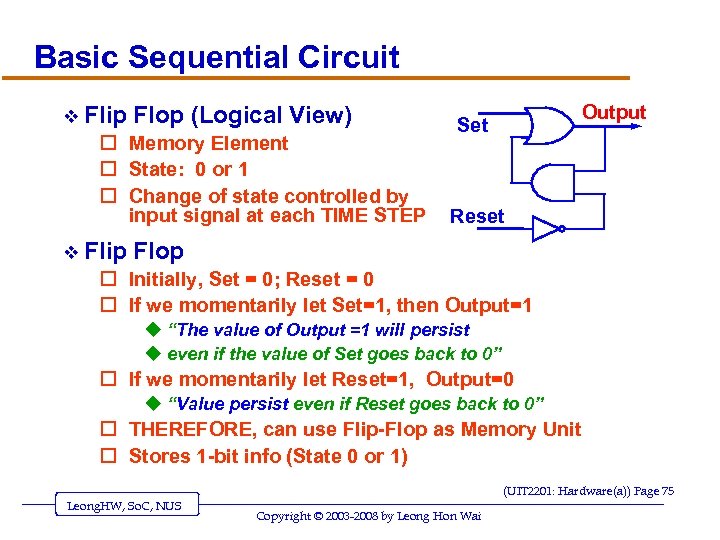 Basic Sequential Circuit v Flip Flop (Logical View) o Memory Element o State: 0 or 1 o Change of state controlled by input signal at each TIME STEP v Flip Output Set Reset Flop o Initially, Set = 0; Reset = 0 o If we momentarily let Set=1, then Output=1 u “The value of Output =1 will persist u even if the value of Set goes back to 0” o If we momentarily let Reset=1, Output=0 u “Value persist even if Reset goes back to 0” o THEREFORE, can use Flip-Flop as Memory Unit o Stores 1 -bit info (State 0 or 1) (UIT 2201: Hardware(a)) Page 75 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Basic Sequential Circuit v Flip Flop (Logical View) o Memory Element o State: 0 or 1 o Change of state controlled by input signal at each TIME STEP v Flip Output Set Reset Flop o Initially, Set = 0; Reset = 0 o If we momentarily let Set=1, then Output=1 u “The value of Output =1 will persist u even if the value of Set goes back to 0” o If we momentarily let Reset=1, Output=0 u “Value persist even if Reset goes back to 0” o THEREFORE, can use Flip-Flop as Memory Unit o Stores 1 -bit info (State 0 or 1) (UIT 2201: Hardware(a)) Page 75 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Summary v Digital computers use binary representations of data: numbers, text, multimedia v Binary values create a bistable environment, making computers reliable v Boolean logic maps easily onto electronic hardware v Circuits are constructed using Boolean expressions as an abstraction v Computational and control circuits may be built from Boolean gates (UIT 2201: Hardware(a)) Page 76 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
Summary v Digital computers use binary representations of data: numbers, text, multimedia v Binary values create a bistable environment, making computers reliable v Boolean logic maps easily onto electronic hardware v Circuits are constructed using Boolean expressions as an abstraction v Computational and control circuits may be built from Boolean gates (UIT 2201: Hardware(a)) Page 76 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
![v If you are new to all these o read the textbook [SG]-Chapter 4 v If you are new to all these o read the textbook [SG]-Chapter 4](https://present5.com/presentation/d8ec9a105f65d73cea7e10f4bf3b025c/image-77.jpg) v If you are new to all these o read the textbook [SG]-Chapter 4 o do the exercises in the book … The End … (UIT 2201: Hardware(a)) Page 77 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
v If you are new to all these o read the textbook [SG]-Chapter 4 o do the exercises in the book … The End … (UIT 2201: Hardware(a)) Page 77 Leong. HW, So. C, NUS Copyright © 2003 -2008 by Leong Hon Wai
 Thank you! (UIT 2201: 4 Hardware(a)) Page 78 Leong. HW, SOC, NUS Copyright © 2007 -2008 by Leong Hon Wai
Thank you! (UIT 2201: 4 Hardware(a)) Page 78 Leong. HW, SOC, NUS Copyright © 2007 -2008 by Leong Hon Wai


