Скачать презентацию Handout 1 SI 760 EECS 597 Скачать презентацию Handout 1 SI 760 EECS 597

56997cc9966277bad8970b010bb5329b.ppt

  • Количество слайдов: 57

Handout #1 SI 760 / EECS 597 / Ling 702 Language and Information Winter Handout #1 SI 760 / EECS 597 / Ling 702 Language and Information Winter 2004

Course Information • Instructor: Dragomir R. Radev (radev@umich. edu) • Office: 3080, West Hall Course Information • Instructor: Dragomir R. Radev (radev@umich. edu) • Office: 3080, West Hall Connector • Phone: (734) 615 -5225 • Office hours: TBA • Course page: http: //www. si. umich. edu/~radev/LNI-winter 2004/ • Class meets on Mondays, 1 -4 PM in 412 WH

Readings • Two introductions to statistical NLP • Collocations paper • Joshua Goodman’s language Readings • Two introductions to statistical NLP • Collocations paper • Joshua Goodman’s language modeling tutorial • Documentation for the CMU LM toolkit

N-gram Models N-gram Models

Word Prediction • • • Example: “I’d like to make a collect …” “I Word Prediction • • • Example: “I’d like to make a collect …” “I have a gub” “He is trying to fine out” “Hopefully, all with continue smoothly in my absence” “They are leaving in about fifteen minuets to go to her house” • “I need to notified the bank of [this problem] • Language model: a statistical model of word sequences

Counting Words • Brown corpus (1 million words from 500 texts) • Example: “He Counting Words • Brown corpus (1 million words from 500 texts) • Example: “He stepped out into the hall, was delighted to encounter a water brother” - how many words? • Word forms and lemmas. “cat” and “cats” share the same lemma (also tokens and types) • Shakespeare’s complete works: 884, 647 word tokens and 29, 066 word types • Brown corpus: 61, 805 types and 37, 851 lemmas • American Heritage 3 rd edition has 200, 000 “boldface forms” (including some multiword phrases)

Unsmoothed N-grams • First approximation: each word has an equal probability to follow any Unsmoothed N-grams • First approximation: each word has an equal probability to follow any other. E. g. , with 100, 000 words, the probability of each of them at any given point is. 00001 • “the” - 69, 971 times in BC, while “rabbit” appears 11 times • “Just then, the white …” P(w 1, w 2, …, wn) = P(w 1) P(w 2 |w 1) P(w 3|w 1 w 2) … P(wn |w 1 w 2…wn-1)

A language model • The sum of probabilities of all strings has to be A language model • The sum of probabilities of all strings has to be 1. • Bigram and trigram models Bigram model: Replace P(wn |w 1 w 2…wn-1) with P(wn|wn-1) • How do you estimate the probabilities?

Perplexity of a language model • What is the perplexity of guessing a digit Perplexity of a language model • What is the perplexity of guessing a digit if all digits are equally likely? • How about a letter? • How about guessing A with a probability of 1/4, B with a probability of 1/2 and 10, 000 other cases with a probability of 1/2 total (example modified from Joshua Goodman).

Perplexity across distributions • What if the actual distribution is very different from the Perplexity across distributions • What if the actual distribution is very different from the expected one? • Example: all of the 10, 000 other cases are equally likely but P(A) = P(B) = 0. • Cross-entropy = log (perplexity), measured in bits

Smoothing techniques • Imagine the following situation: you are looking at Web pages and Smoothing techniques • Imagine the following situation: you are looking at Web pages and you have to guess how many different languages they are written in. • First one is in English, then French, then again English, then Korean, then Chinese, etc. Total: 5 F, 3 E, 1 K, 1 C • Can you predict what the next language will be? • What is a problem with the simplest approach to this problem?

Smoothing • Why smoothing? • How many parameters are there in the model (given Smoothing • Why smoothing? • How many parameters are there in the model (given 100, 000 possible words) • What are the unsmoothed (ML) estimates for unigrams, bigrams, trigrams? • Linear interpolation (mixture with λi). • How to estimate λi?

Example • Consider the problem of estimating bigram probabilities from a training corpus. • Example • Consider the problem of estimating bigram probabilities from a training corpus. • Probability mass must be 1. • How to account for unseen events?

Common methods • Add-1 smoothing (add one to numerator, add N to denominator) • Common methods • Add-1 smoothing (add one to numerator, add N to denominator) • Good-Turing smoothing • Best: Kneser-Ney

Markov Models • Assumption: we can predict the probability of some future item on Markov Models • Assumption: we can predict the probability of some future item on the basis of a short history • Bigrams: first-level Markov models • Bigrammars: as an N-by-N matrix of probabilities, where N is the size of the vocabulary that we are modeling.

Relative Frequencies Relative Frequencies

Language Modeling and Statistical Machine Translation Language Modeling and Statistical Machine Translation

The Noisy Channel Model • Source-channel model of communication • Parametric probabilistic models of The Noisy Channel Model • Source-channel model of communication • Parametric probabilistic models of language and translation • Training such models

Statistics • Given f, guess e e E F f e’ F E encoder Statistics • Given f, guess e e E F f e’ F E encoder decoder e’ = argmax P(e|f) = argmax P(f|e) P(e) e e translation model language model

Parametric probabilistic models • Language model (LM) P(e) = P(e 1, e 2, …, Parametric probabilistic models • Language model (LM) P(e) = P(e 1, e 2, …, e. L) = P(e 1) P(e 2|e 1) … P(e. L|e 1 … e. L-1) • Deleted interpolation P(e. L|e 1 … e. K-1) P(e. L|e. L-2, e. L-1) • Translation model (TM) Alignment: P(f, a|e)

IBM’s EM trained models 1. 2. 3. 4. 5. Word translation Local alignment Fertilities IBM’s EM trained models 1. 2. 3. 4. 5. Word translation Local alignment Fertilities Class-based alignment Non-deficient algorithm (avoid overlaps, overflow)

Bayesian formulas • argmaxe P(e | f) = ? • P(e|f) = P(e) * Bayesian formulas • argmaxe P(e | f) = ? • P(e|f) = P(e) * P(f | e) / P(f) • argmaxe P(e | f) = argmaxe P(e) * P(f | e) The rest of the slides in this section are based on “A Statistical MT Tutorial Workbook” by Kevin Knight

N-gram model • P(e) = ? • P(how's it going? ) = 76, 413/1, N-gram model • P(e) = ? • P(how's it going? ) = 76, 413/1, 000, 000 = 0. 000076413 • Bigrams: b(y|x) = count (xy)/count (x) • P(“I like snakes that are not poisonous”) = P(“I”|start) * P(“like”|”I”) * … • Trigrams: b(z|xy) = ? ?

Smoothing • b(z | x y) = 0. 95 * count (“xyz”) / count Smoothing • b(z | x y) = 0. 95 * count (“xyz”) / count (“xy”) + 0. 04 * count (“yz”) / count (“z”) + 0. 008 * count (“z”) / totalwordsseen + 0. 002

Ordering words (1) a a centre earthquake evacuation forced has historic Italian of of Ordering words (1) a a centre earthquake evacuation forced has historic Italian of of second southern strong the village (2) met Paul Wendy

Translation models • • Mary did not slap the green witch. Mary not slap Translation models • • Mary did not slap the green witch. Mary not slap the green witch Mary no daba una botefada a la verde bruja Mary no daba una botefada a la bruja verde

Translation models • Fertility • Permutation Translation models • Fertility • Permutation

IBM model 3 • • Fertility Spurious words (e 0) Pick words Pick positions IBM model 3 • • Fertility Spurious words (e 0) Pick words Pick positions

Translation models • • • Mary did not slap the green witch. Mary not Translation models • • • Mary did not slap the green witch. Mary not slap the green witch Mary not slap NULL the green witch Mary no daba una botefada a la verde bruja Mary no daba una botefada a la bruja verde

Parameters • • N - fertility (x*x) T - translation (x) D - position Parameters • • N - fertility (x*x) T - translation (x) D - position (x) P

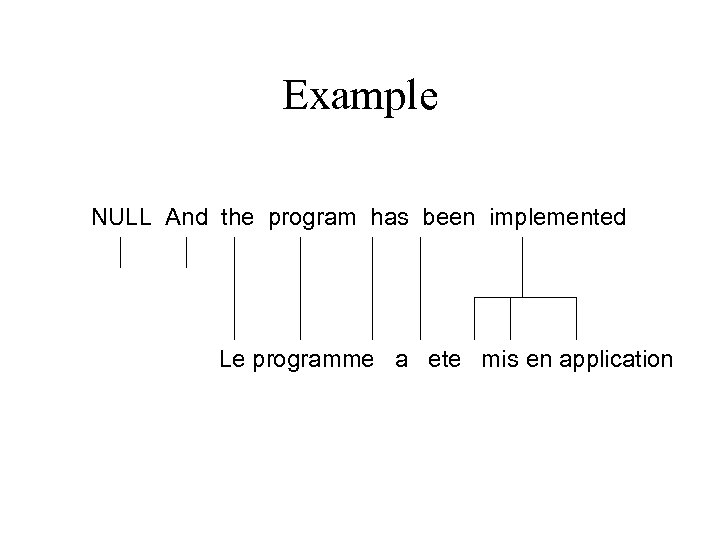Example NULL And the program has been implemented Le programme a ete mis en Example NULL And the program has been implemented Le programme a ete mis en application

Alignments The blue house La maison bleue • Needed: P(a|f, e) Alignments The blue house La maison bleue • Needed: P(a|f, e)

Markov models Markov models

Motivation • Sequence of random variables that aren’t independent • Example: weather reports Motivation • Sequence of random variables that aren’t independent • Example: weather reports

Properties • Limited horizon: P(Xt+1 = sk|X 1, …, Xt) = P(Xt+1 = sk|Xt) Properties • Limited horizon: P(Xt+1 = sk|X 1, …, Xt) = P(Xt+1 = sk|Xt) • Time invariant (stationary): = P(X 2=sk|X 1) • Definition: in terms of a transition matrix A and initial state probabilities .

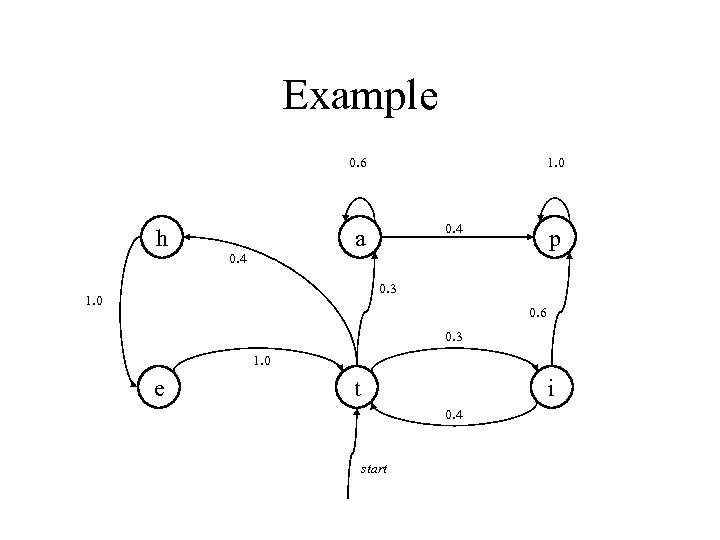Example 0. 6 h 1. 0 0. 4 a 0. 4 p 0. 3 Example 0. 6 h 1. 0 0. 4 a 0. 4 p 0. 3 1. 0 0. 6 0. 3 1. 0 e t i 0. 4 start

Visible MM P(X 1, …XT) = P(X 1) P(X 2|X 1) P(X 3|X 1, Visible MM P(X 1, …XT) = P(X 1) P(X 2|X 1) P(X 3|X 1, X 2) … P(XT|X 1, …, XT-1) = P(X 1) P(X 2|X 1) P(X 3|X 2) … P(XT|XT-1) P(t, i, p) = P(X 1=t) P(X 2=i|X 1=t) P(X 3=p|X 2=i) = 1. 0 x 0. 3 x 0. 6 = 0. 18

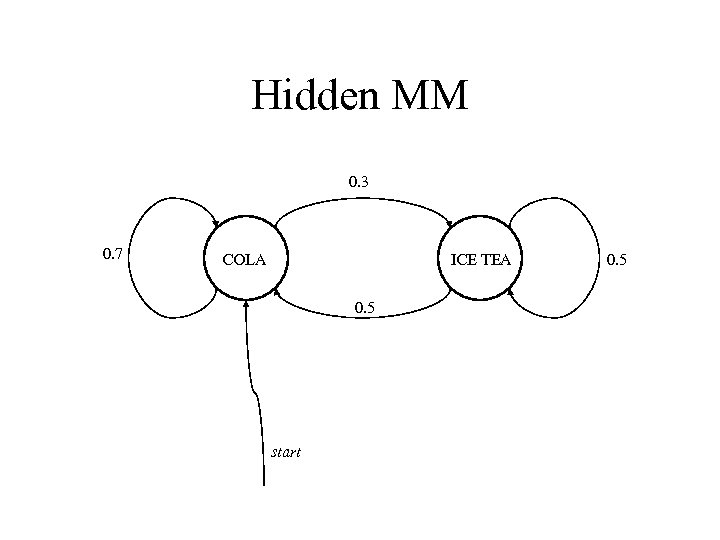Hidden MM 0. 3 0. 7 COLA ICE TEA 0. 5 start 0. 5 Hidden MM 0. 3 0. 7 COLA ICE TEA 0. 5 start 0. 5

Hidden MM • P(Ot=k|Xt=si, Xt+1=sj) = bijk cola icetea lemonade COLA 0. 6 0. Hidden MM • P(Ot=k|Xt=si, Xt+1=sj) = bijk cola icetea lemonade COLA 0. 6 0. 1 0. 3 ICETEA 0. 1 0. 7 0. 2

Example • P(lemonade, icetea|COLA) = ? • P = 0. 7 x 0. 3 Example • P(lemonade, icetea|COLA) = ? • P = 0. 7 x 0. 3 x 0. 7 x 0. 1 + 0. 7 x 0. 3 x 0. 1 + 0. 3 x 0. 5 x 0. 7 = 0. 084

Hidden MM • Part of speech tagging, speech recognition, gene sequencing • Three tasks: Hidden MM • Part of speech tagging, speech recognition, gene sequencing • Three tasks: – A=state transition probabilities, B=symbol emission probabilities, = initial state prob. – Given = (A, B, ), find P(O| ) – Given O, , what is (X 1, …XT+1) – Given O and a space of all possible , find model that best describes the observations

Collocations Collocations

Collocations • Idioms • Free word combinations • Know a word by the company Collocations • Idioms • Free word combinations • Know a word by the company that it keeps (Firth) • Common use • No general syntactic or semantic rules • Important for non-native speakers

Examples Idioms Collocations Free-word combinations To kick the bucket Dead end To catch up Examples Idioms Collocations Free-word combinations To kick the bucket Dead end To catch up To trade actively Table of contents Orthogonal projection To take the bus The end of the road To buy a house

Uses • Disambiguation (e. g, “bank”/”loan”, ”river”) • Translation • Generation Uses • Disambiguation (e. g, “bank”/”loan”, ”river”) • Translation • Generation

Properties • • • Arbitrariness Language- and dialect-specific Common in technical language Recurrent in Properties • • • Arbitrariness Language- and dialect-specific Common in technical language Recurrent in context (see Smadja 83)

Arbitrariness • Make an effort vs. *make an exertion • Running commentary vs. *running Arbitrariness • Make an effort vs. *make an exertion • Running commentary vs. *running discussion • Commit treason vs. *commit treachery

Cross-lingual properties • Régler la circulation = direct traffic • Russian, German, Serbo-Croatian: direct Cross-lingual properties • Régler la circulation = direct traffic • Russian, German, Serbo-Croatian: direct translation is used • AE: set the table, make a decision • BE: lay the table, take a decision • “semer le désarroi” - “to sow disarray” - “to wreak havoc”

Types of collocations • Grammatical: come to, put on; afraid that, fond of, by Types of collocations • Grammatical: come to, put on; afraid that, fond of, by accident, witness to • Semantic (only certain synonyms) • Flexible: find/discover/notice by chance

Base/collocator pairs Base Collocator Example Noun Verb Adjective Verb verb adjective adverb preposition Set Base/collocator pairs Base Collocator Example Noun Verb Adjective Verb verb adjective adverb preposition Set the table Warm greetings Struggle desperately Sound asleep Put on

Extracting collocations • Mutual information I (x; y) = log 2 • What if Extracting collocations • Mutual information I (x; y) = log 2 • What if I(x; y) = 0? • What if I(x; y) < 0? P(x, y) P(x)P(y)

Yule’s coefficient A - frequency of lemma pairs involving both Li and Lj B Yule’s coefficient A - frequency of lemma pairs involving both Li and Lj B - frequency of pairs involving Li only C - frequency of pairs involving Lk only D - frequency of pairs involving neither YUL = AD - BC AD + BC -1 YUL 1

Specific mutual information • Used in extracting bilingual collocations I (e, f) = p Specific mutual information • Used in extracting bilingual collocations I (e, f) = p (e, f) p(e) p(f) • p(e, f) - probability of finding both e and f in aligned sentences • p(e), p(f) - probabilities of finding the word in one of the languages

Example from the Hansard corpus (Brown, Lai, and Mercer) Example from the Hansard corpus (Brown, Lai, and Mercer)

Flexible and rigid collocations • Example (from Smadja): “free” and “trade” Flexible and rigid collocations • Example (from Smadja): “free” and “trade”

Xtract (Smadja) • The Dow Jones Industrial Average • The NYSE’s composite index of Xtract (Smadja) • The Dow Jones Industrial Average • The NYSE’s composite index of all its listed common stocks fell *NUMBER* to *NUMBER*

Translating Collocations • Brush up a lesson, repasser une leçon • Bring about/осуществлять • Translating Collocations • Brush up a lesson, repasser une leçon • Bring about/осуществлять • Hansards: late spring: fin du printemps, Atlantic Canada Opportunities Agency, Agence de promotion économique du Canada atlantique