Гусакова В. И. , Кривошлыков В. Н. , Шепелова Н. С. Математика. Задачи линейного программирования. Методические рекомендации для самостоятельной работы студентов. Учебно-метод. пособие. - Ростов н/Д: Изд-во СКАГС, 2011. В. И. Гусакова МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ Учебно-методический комплекс по направлению «Экономика» (бакалавр) Ростов-на-Дону 2012 1
Общая задача линейного программирования имеет вид: Линейная функция f называется целевой функцией задачи. Все остальное, за исключением условий неотрицательности переменных xj, - ограничения. 2
Геометрический метод решения задач ЛП Применение метода к задачам с двумя переменными. Пусть дана задача ЛП в виде: Каждое ограничение геометрически определяет полуплоскость, следовательно, множество допустимых решений Х представляет собой пересечение конечного числа полуплоскостей, т. е. если Х (не пустое множество), то Х есть либо многоугольник либо многоугольное множество. 3
Целевая функция Рассмотрим целевую функцию f(x)=c 1 x 1+c 2 x 2 Линии уровня c 1 x 1+c 2 x 2=a образуют прямых. семейство параллельных Вектор n=(c 1, c 2) является вектором нормали к этим прямым и показывает направление возрастания целевой функции. Вектор –с будет показывать направление убывания целевой функции. 4
Теорема Целевая функция задачи ЛП достигает своего экстремального значения в угловой точке многогранника решений. 5
Алгоритм графического метода 1. Построить область допустимых решений (ДР). 2. Если область ДР – пустое множество, то задача не имеет решения ввиду несовместности системы ограничений. 3. Если область ДР является непустым множеством, строим нормаль линий уровня и одну из линий. 4. Перемещаем линию уровня до опорной прямой в задаче на максимум в направлении нормали, а в задаче на минимум- в противоположном направлении. 5. Если при перемещении линии уровня по области ДР в направлении, соответствующем приближению к экстремуму, линии уровня уходят в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции. 6. Если задача ЛП имеет оптимальное решение, то для его нахождения необходимо решить совместно уравнения прямых, ограничивающих область ДР и имеющих общие точки с соответствующей опорной прямой. 7. Если целевая функция достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. 6
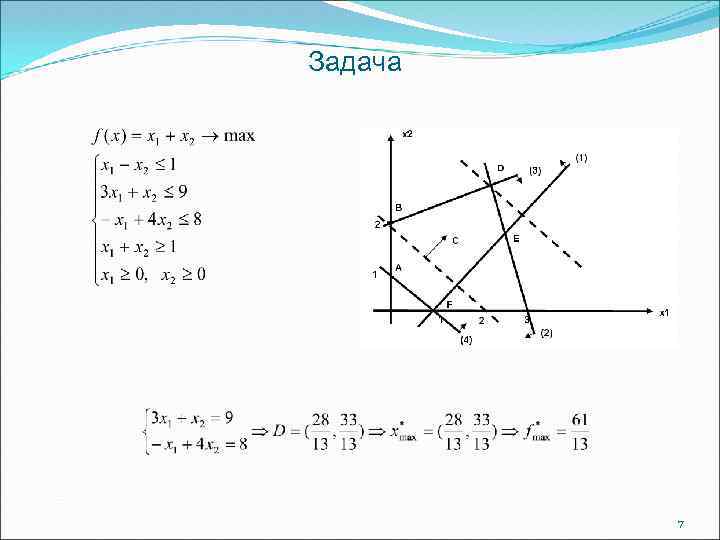Задача 7
Каноническая форма задач ЛП Будем считать, что задача линейного программирования записана в канонической форме, если: 1. её целевая функция максимизируется; 2. ограничения имеют вид равенств с неотрицательной правой частью; 3. и все переменные неотрицательны. 8
Привести к каноническому виду → ↓ 9
Двойственность в линейном программировании Двойственная задача- это вспомогательная задача ЛП, получаемая с помощью определенных правил непосредственно из условий исходной задачи. 1. Если целевая функция f исходной задачи максимизируется, то целевая функция z двойственной задачи – минимизируется и наоборот. 2. Количество ограничений (m) исходной задачи равно количеству переменных двойственной задачи, а количество переменных (n) исходной задачи равно количеству ограничений двойственной. Переменные двойственной задачи обозначим yi (i=1, 2, m). 3. Поскольку переменные исходной задачи связаны с ограничениями двойственной, то каждой переменной xj 0 соответствует в двойственной задаче ограничения вида « » (f→max) или « » (f→min) и наоборот. 10
4. Каждой переменной xj неограниченной по знаку, соответствует ограничение вида «=» двойственной задачи, и наоборот. 5. Свободные члены ограничений исходной задачи bi (i=1, 2. . m) в двойственной задаче являются коэффициентами при переменных yi (i=1, 2, m) в целевой функции z. Коэффициенты cj (j=1, 2 n) при переменных xj (j=1, 2 n) в целевой функции исходной задачи являются свободными членами ограничений двойственной. 6. Матрица А коэффициентов при неизвестных в ограничениях исходной задачи в двойственной задаче транспонируется АТ. 11
Задача А Переменные, соответствующие ограничениям задачи А. Переменные, Задача В соответст(двойственная вующие к задаче А) ограничениям задачи В. y 1 y 2 y 3 x 1 x 2 12
Транспортная задача Пусть имеется m поставщиков А 1, А 2, …Аm однородного груза в количества а 1, а 2, аm единиц и n потребителей В 1, В 2, …Вn этого груза, потребность которых составляет соответственно в 1, в 2, вn единиц. Известны стоимости перевозок единицы груза от i-го поставщика к j-му потребителю сij (i=1, 2, …m, j=1, 2, …n). Требуется составить такой план перевозок, который обеспечит минимальные транспортные расходы. Исходные данные транспортной задачи записываются в виде таблицы 13
Переменные хij (i=1, 2, …m, j=1, 2, …n) – объемы перевозок от каждого от i-го поставщика к j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок. 14
Математическая модель транспортной задачи в общем случае имеет вид: 15
Целевая функция задачи (А) выражает требование обеспечить минимум суммарных затрат на перевозку всех грузов. Группа из m уравнений (В) описывает тот факт, что запасы всех m поставщиков вывозятся полностью. Группа из n уравнений (С) выражает требование полностью удовлетворить запросы всех n потребителей. Неравенство (D) является условиями неотрицательности всех переменных задачи. Таким образом математическая формулировка транспортной задачи состоит в следующем: Найти матрицу Х =( хij ) i=1, 2, …m, j=1, 2, …n, элементы которой удовлетворяют системе ограничений (В) и (С), условиям неотрицательности (D) и обеспечивают минимум целевой функции (А). 16
В рассматриваемой модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей т. е Такая задача называется задачей с правильным балансом, а её модель закрытой. Если это равенство не выполняется, то модель называется задачей с неправильным балансом, а её модель – открытой. 17
Метод северо-западного угла Согласно этому методу запасы очередного Поставщика используются для обеспечения запросов очередных Потребителей до тех пор, пока не будут исчерпаны полностью. После чего используются запасы следующего по номеру Поставщика. Заполнение таблицы транспортной задачи начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного Поставщика и запросов очередного Потребителя заполняется только одна клетка и соответственно исключается из рассмотрения один Поставщик или Потребитель. Во избежании ошибок после построения начального базисного (опорного) решения необходимо проверить , что число занятых клеток равно m+n-1. Пример. 18
Метод потенциалов Если допустимое решение Х =( хij ) i=1, 2, …m, j=1, 2, …n транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков ui (i=1, 2, …m) и потребителей vj (j=1, 2, …n), удовлетворяющие следующим условиям Группа равенств (1) используется как система уравнений для нахождения потенциалов. Так как число неизвестных системы на единицу больше числа уравнений, то одной из них можно задать значение произвольно, а остальные найти из системы. 19
Группа неравенств (2) используется для проверки оптимальности опорного решения. Эти неравенства удобнее представить в следующем виде. Числа называются оценками для свободных клеток таблицы (векторов условий) транспортной задачи. 20
Опорное решение является оптимальным, если для всех векторов условий (клеток таблицы) оценки неположительные. Оценки для свободных клеток транспортной таблицы используются для улучшения опорного решения. Для этого находят клетку (l, k) таблицы, соответствующую. Если , то решение оптимальное. Если , то для соответствующей клетки (l, k) строят цикл и улучшают решение, перераспределяя груз по этому циклу. При этом целевая функция уменьшается на величину . Особенности решения транспортных задач с неправильным балансом. 21