GRL Dynamic Pile testing with the Pile Driving

GRL Dynamic Pile testing with the Pile Driving Analyzer® © 1998 Goble Rausche Likins and Associates and Dr. Julian Seidel

GRL • • Summary History of Dynamic Pile Testing Measuring stress waves Fundamentals of Wave Mechanics The Case Method (Pile Driving Analyzer) – Capacity – Stresses – Integrity – Hammer performance

GRL History of Dynamic Pile Testing/Analysis 18 th Century: Closed Form Solutions Late 19 th Century: Engineering News Formula 1920’s: First Strain Measurements 1950: Smith’s Wave Equation Program 1964: Case Project began under Dr. G. G. Goble 1968: Pile Driving Analyzer ® (PDA) 1970: CAPWAP ® 1972: Pile Dynamics, Inc. founded 1976: WEAP program 1977: Saximeter 1982: Hammer Performance Analyzer 1986: Hammer Performance Study 1989: Pile Integrity Testing (PIT) 1996: FHWA Manual 1998: Pile Installation Recorders (PIR) 1999: Remote PDA

GRL 1 -D Wave Theory • Hammer causes a downward travelling stress-wave to enter the pile • Soil resistance causes stress-wave reflections • Stress in pile can be represented by 1 -dimensional Wave Theory • These stress-waves can be measured and identified with measurement of force and velocity near the pile top

GRL Newtonian Collision Analogy v 1 m 2 v 1 W 2 Pile is a longitudinally-distributed mass Hammer is a concentrated mass “Rigid body” motion assumption is not reasonable “Rigid body” motion assumption is reasonable Motion is dominated by stress-wave effects

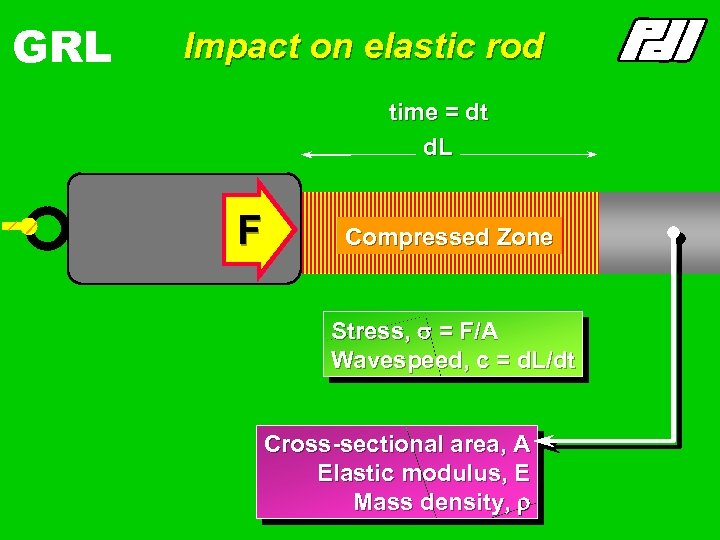GRL Impact on elastic rod time = dt d. L F Compressed Zone Stress, s = F/A Wavespeed, c = d. L/dt Cross-sectional area, A Elastic modulus, E Mass density, r

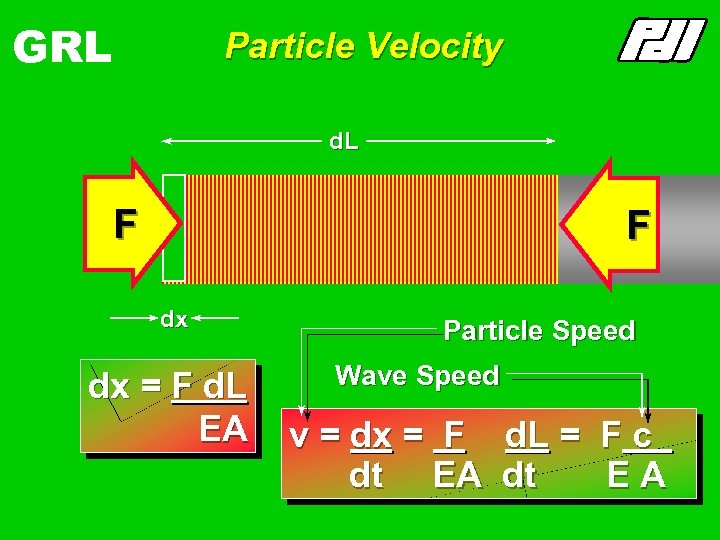GRL Particle Velocity d. L FF F dx dx = F d. L EA Particle Speed Wave Speed v = dx = F dt EA d. L = dt Fc EA

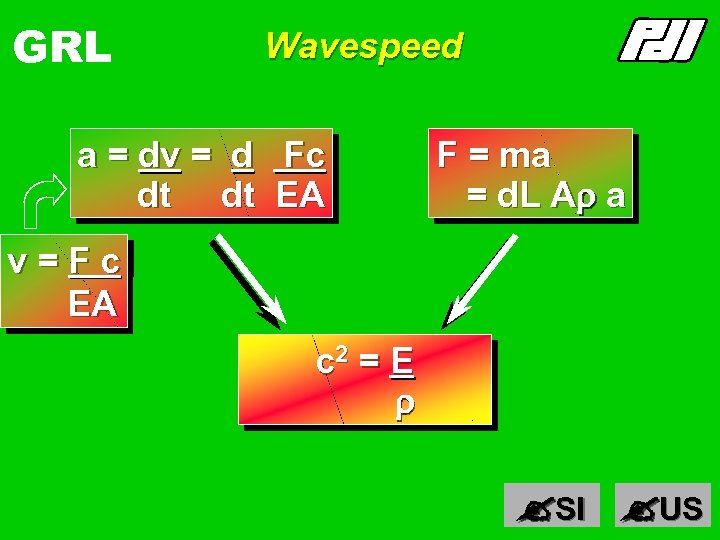GRL Wavespeed a = dv = d dt dt v=Fc EA F = ma = d. L Ar a d. L F = d. L = E F c 1 c 2 A r 1 c dt r. E A Cross-sectional area, A Mass density, r SI US

GRL Force, velocity, stress and strain Particle Speed Wave Speed Pile Impedance v = d x = F d. L = Fc dt EA F=s=v. E A c F = EAv c = Zv s=e=v E c SI US

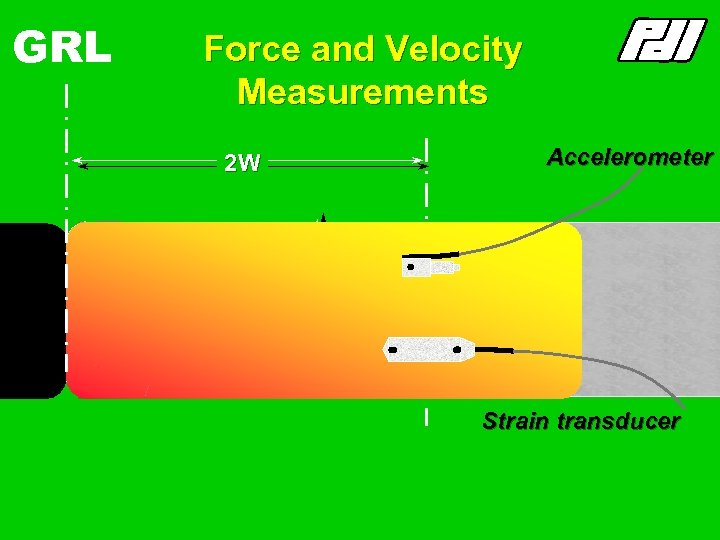GRL Force and Velocity Measurements Accelerometer 2 W W Strain transducer

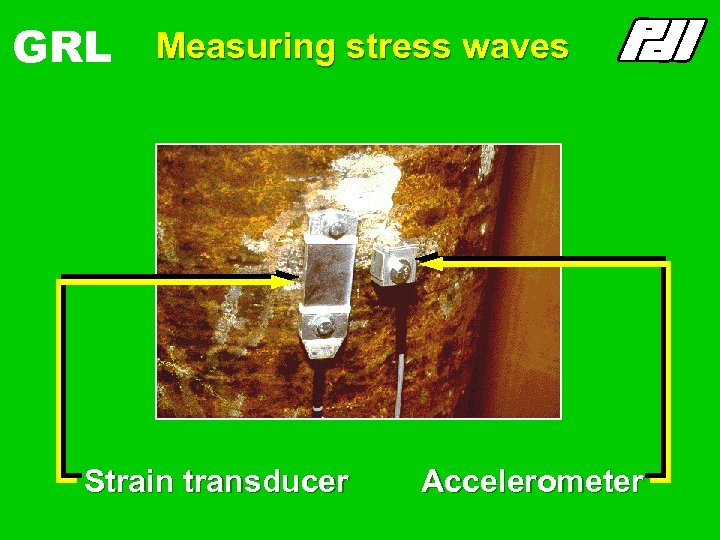GRL Measuring stress waves Strain transducer Accelerometer

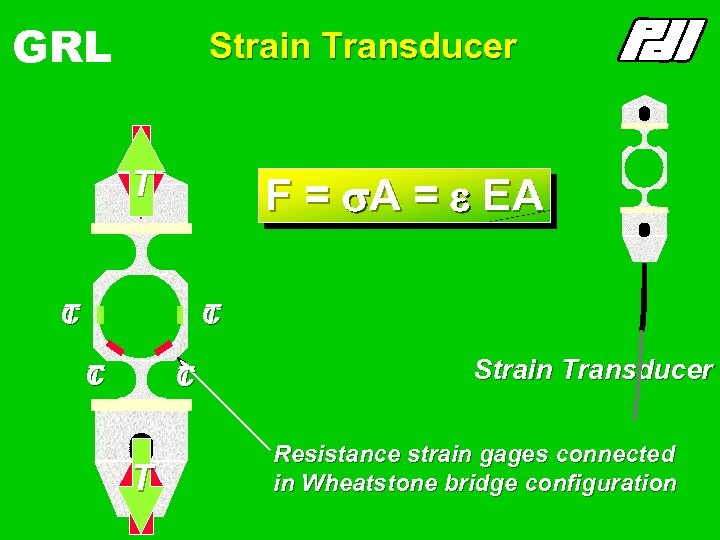GRL Strain Transducer C T F = s. A = e EA C T C T T C Strain Transducer Resistance strain gages connected in Wheatstone bridge configuration

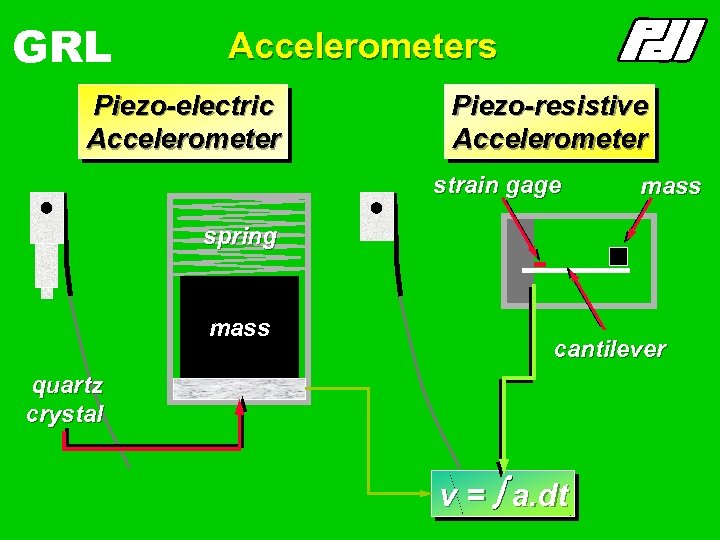GRL Accelerometers Piezo-electric Accelerometer Piezo-resistive Accelerometer strain gage mass spring mass cantilever quartz crystal v = a. dt

GRL Sign Conventions Force: • Compression - positive (+) • Tension - negative (-) Velocity: • Downward - positive (+) • Upward- negative (-)

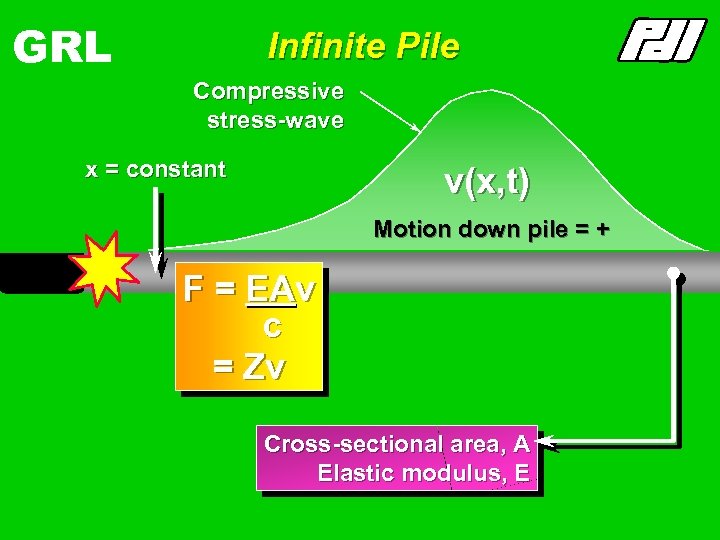GRL Infinite Pile Compressive stress-wave x = constant v(x, t) F(x, t) Motion down = +ve + Compression pile =c Wavespeed, F = EAv c = Zv Cross-sectional area, A Elastic modulus, E

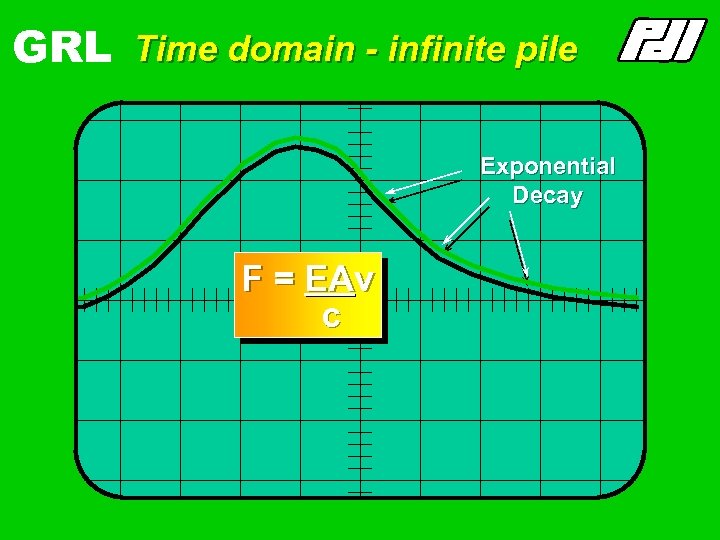GRL Time domain - infinite pile Exponential Decay F = EAv c

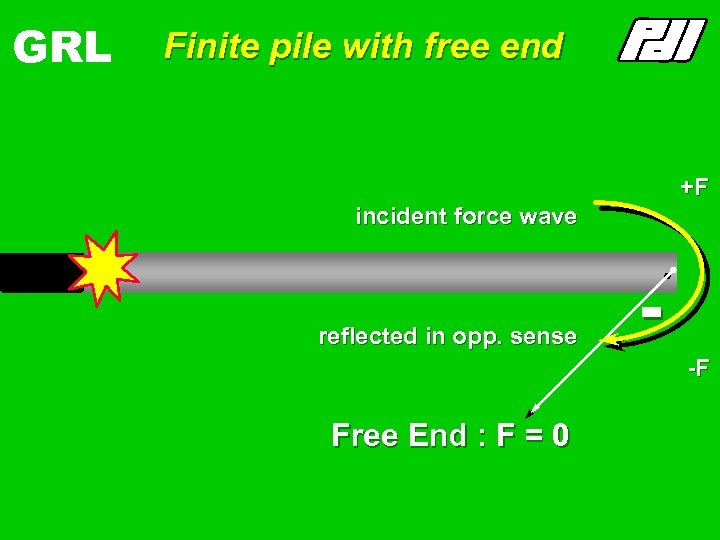GRL Finite pile with free end + +F incident force wave reflected in opp. sense -F Free End : F = 0

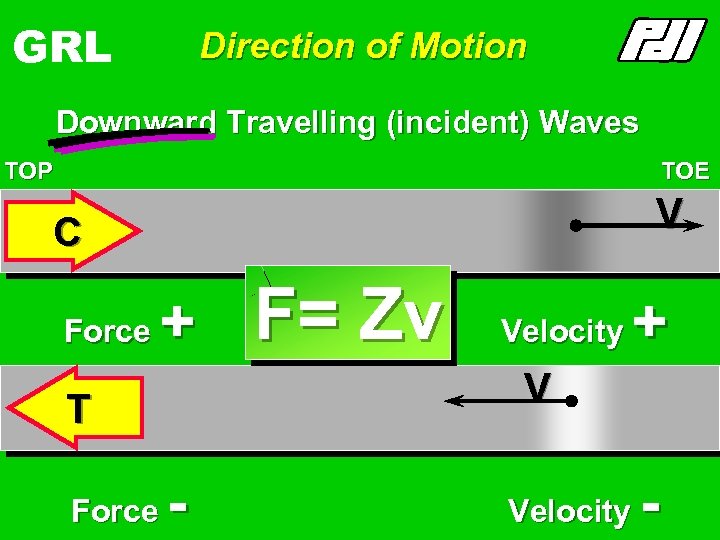GRL Direction of Motion Downward Travelling (incident) Waves TOP TOE V C Force + Velocity + V T Force F= Zv - Velocity -

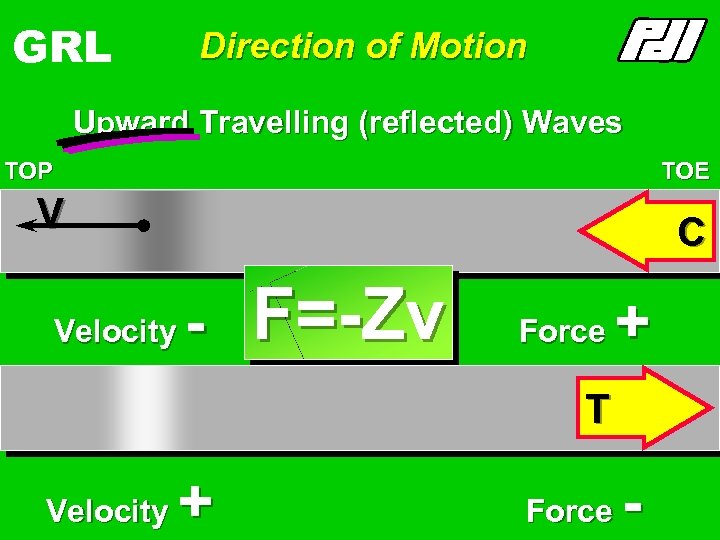GRL Direction of Motion Upward Travelling (reflected) Waves TOP TOE V C Velocity - V Velocity + F=-Zv Force + T Force -

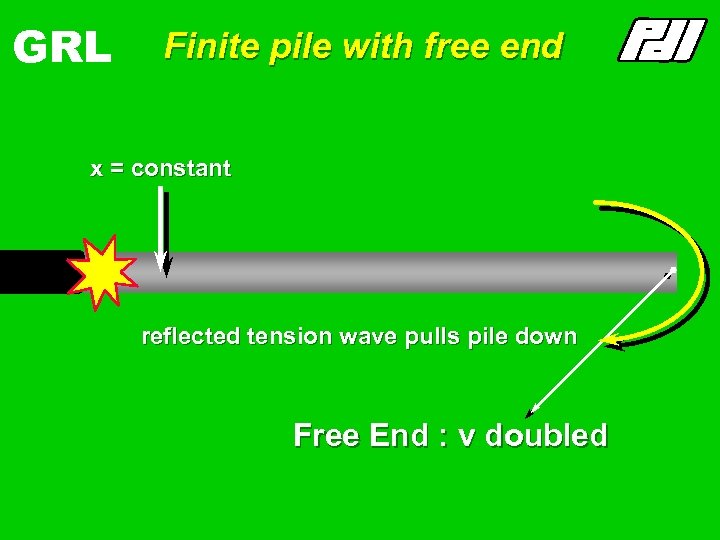GRL Finite pile with free end F- , v+ F+, x = constant + incident wave pushes pile down +v +v + reflected tension wave pulls pile down Free End : v doubled

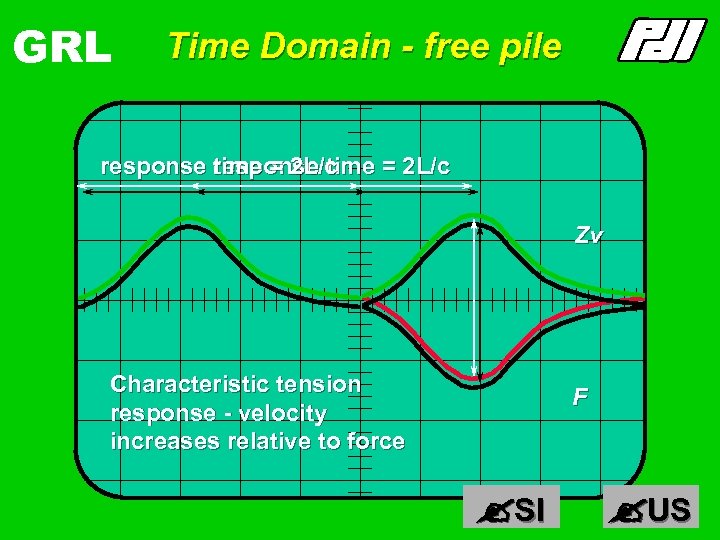GRL Time Domain - free pile response time = 2 L/c Zv Characteristic tension response - velocity increases relative to force F SI US

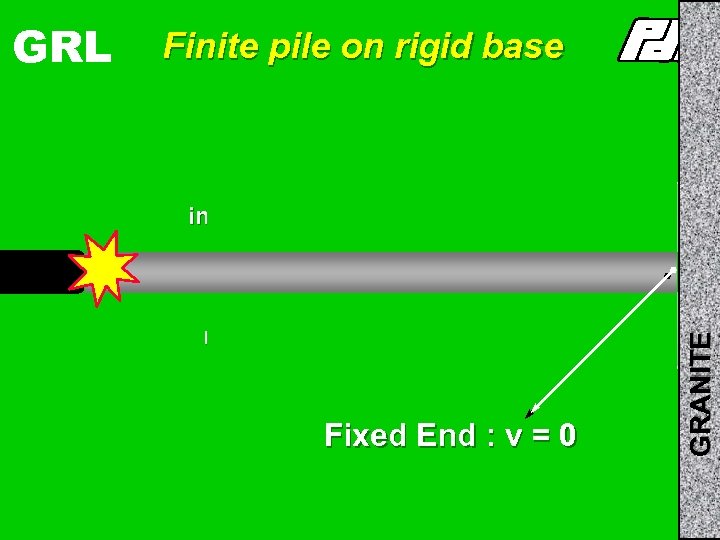Finite pile on rigid base + +v incident wave pushes pile down reflected wave pushes pile up -v Fixed End : v = 0 GRANITE GRL

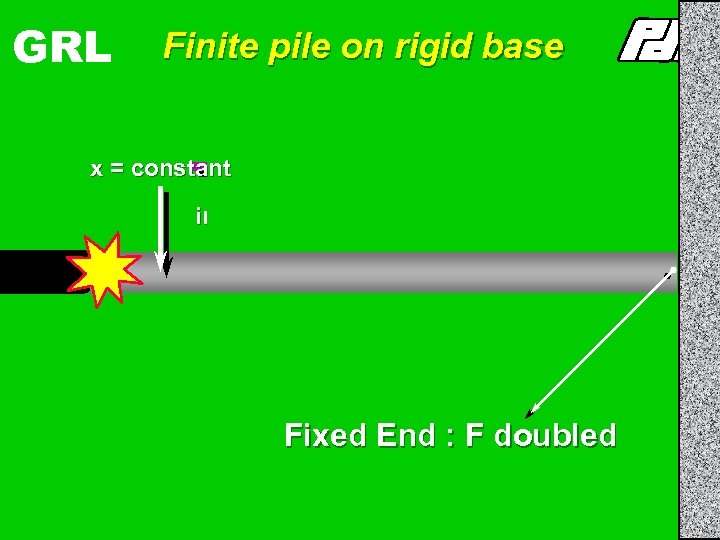Finite pile on rigid base v- , F+ v+, x = constant +C incident wave pushes pile down +F +F +C reflected wave pushes pile up Fixed End : F doubled GRANITE GRL

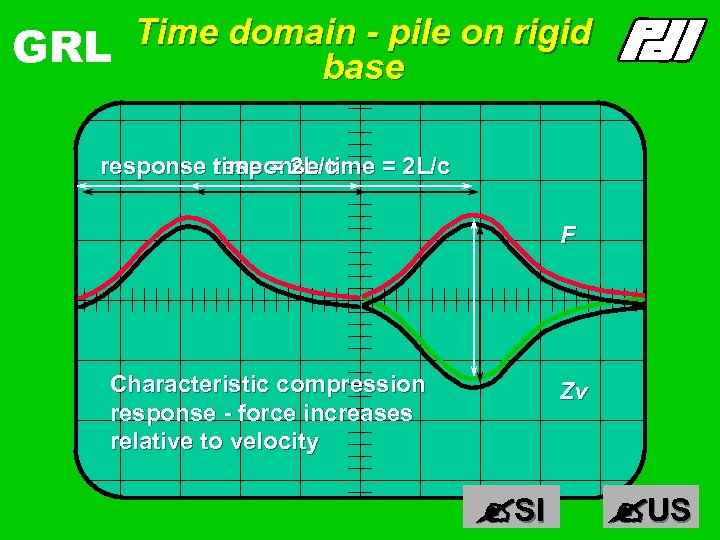GRL Time domain - pile on rigid base response time = 2 L/c F Characteristic compression response - force increases relative to velocity Zv SI US

GRL Separation of Waves Downward Waves Upward Waves Fê=½(F+Zv) FFé½(F-Zv) Fê=Zvê é= =-Zvé F = Fê+ Fé E=mc 2 SI US v = vê+ vé

GRL Waves example (SI) • At impact a 300 mmx 6 mm wall Grade 250 steel pipe pile achieves a peak velocity of 5. 34 m/s, 10 m above ground level. At time 2 L/c later, the force and velocity are measured at 1620 k. N and -2. 67 m/s. What are the upward and downward waves at impact and 2 L/c later? Answer • EA/c = 210, 000 x 5542 x 10 -3/5120= 227 k. Ns/m • At impact Fd = 227 x 5. 34 = 1214 k. N; Fu = 0 k. N • At 2 L/c Fd = ½(1620+227 x-2. 67) = 507 k. N • At 2 L/c Fu = ½(1620 -227 x-2. 67) = 1113 k. N

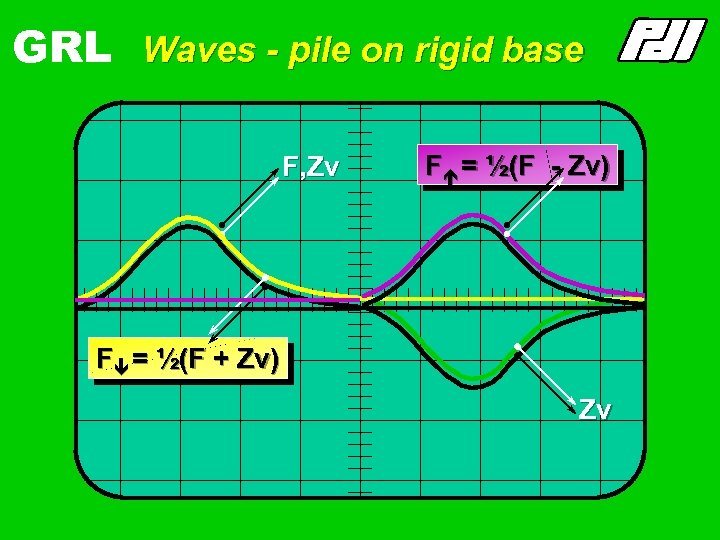GRL Waves - pile on rigid base F, Zv Fé = ½(F - F Zv) Fê = ½(F + Zv) Zv

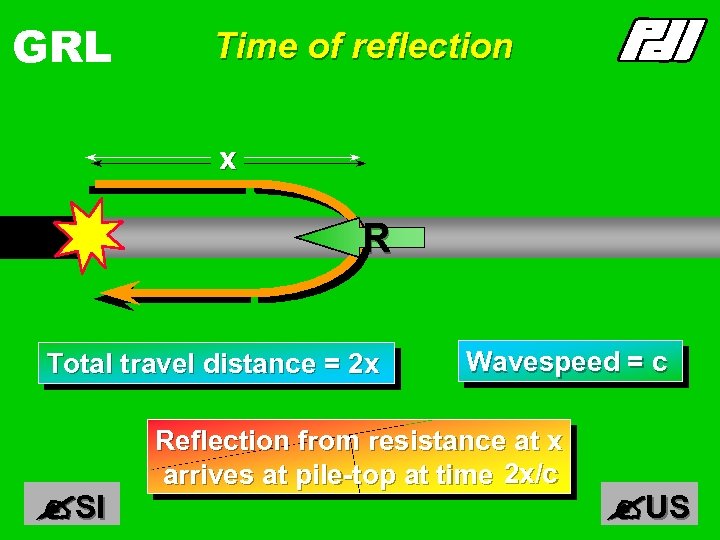GRL Time of reflection x R Total travel distance = 2 x SI Wavespeed = c Reflection from resistance at x arrives at pile-top at time 2 x/c US

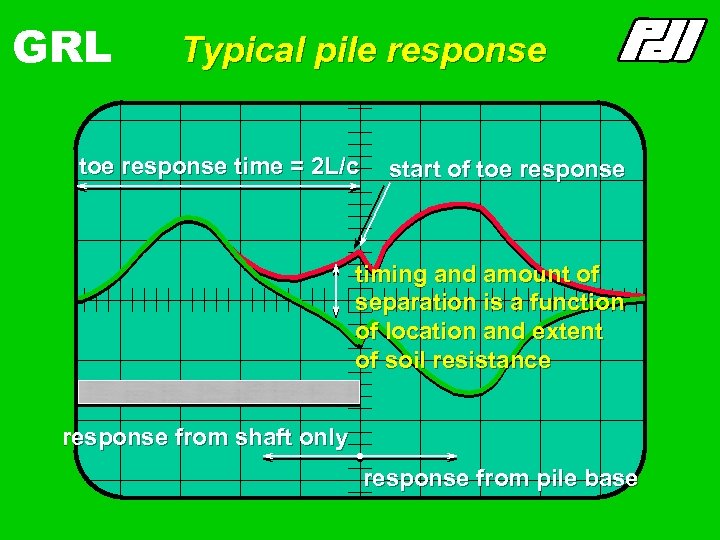GRL Typical pile response toe response time = 2 L/c start of toe response timing and amount of separation is a function of location and extent of soil resistance response from shaft only response from pile base

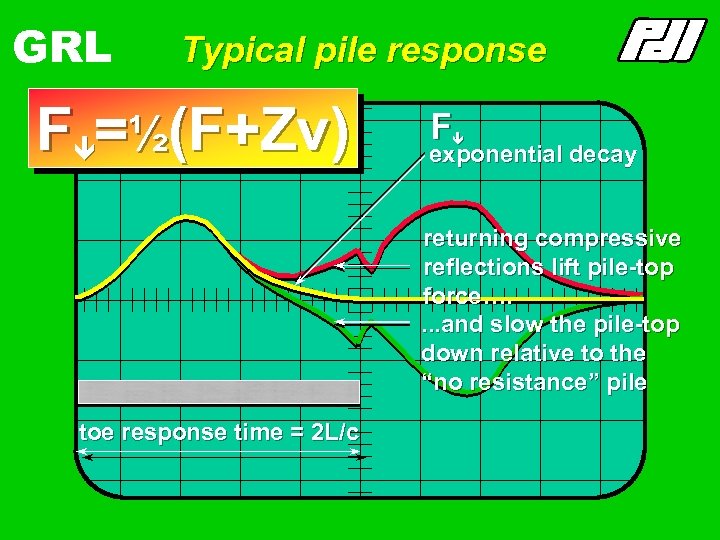GRL Typical pile response Fê=½(F+Zv) F ê exponential decay returning compressive reflections lift pile-top force…. . and slow the pile-top down relative to the “no resistance” pile toe response time = 2 L/c

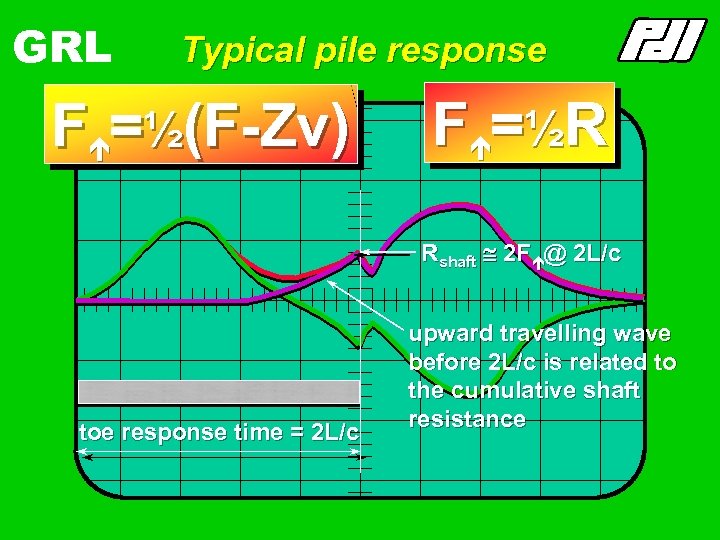GRL Typical pile response Fé=½(F-Zv) Fé=½R Rshaft @ 2 Fé@ 2 L/c toe response time = 2 L/c upward travelling wave before 2 L/c is related to the cumulative shaft resistance

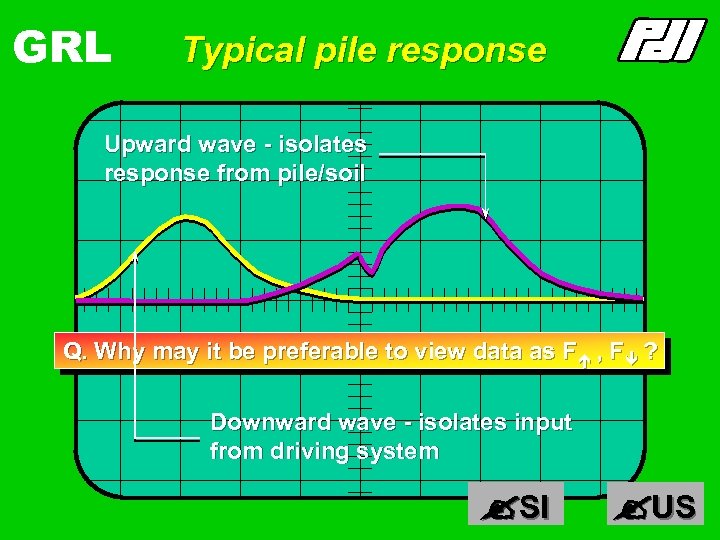GRL Typical pile response Upward wave - isolates response from pile/soil Q. Why may it be preferable to view data as Fé , Fê ? Downward wave - isolates input from driving system SI US

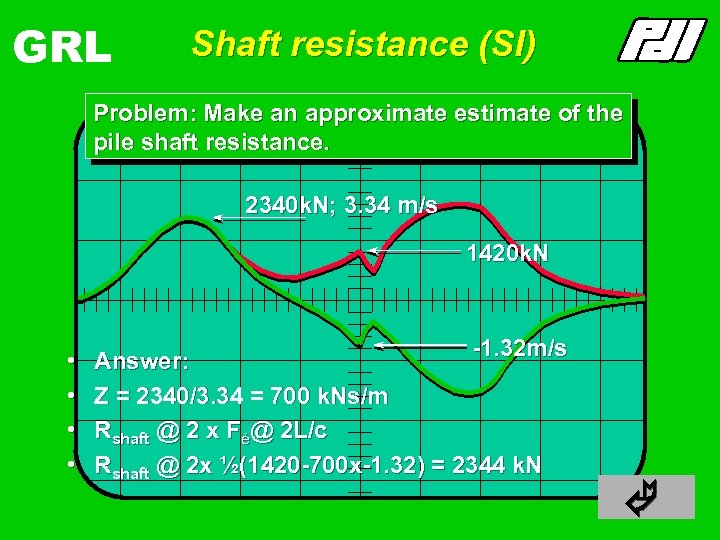GRL Shaft resistance (SI) Problem: Make an approximate estimate of the pile shaft resistance. 2340 k. N; 3. 34 m/s 1420 k. N • • -1. 32 m/s Answer: Z = 2340/3. 34 = 700 k. Ns/m Rshaft @ 2 x Fé@ 2 L/c Rshaft @ 2 x ½(1420 -700 x-1. 32) = 2344 k. N

GRL Conclusion • Pile driving events can be evaluated using 1 -D Wave Mechanics principles • Stress-waves cause changes in force and particle velocity • Force and velocity are related by the pile impedance • Waves travelling both up and down a pile can be separated by F and V measurement • Soil resistance causes reflections which can be interpreted to determine extent and location of resistance

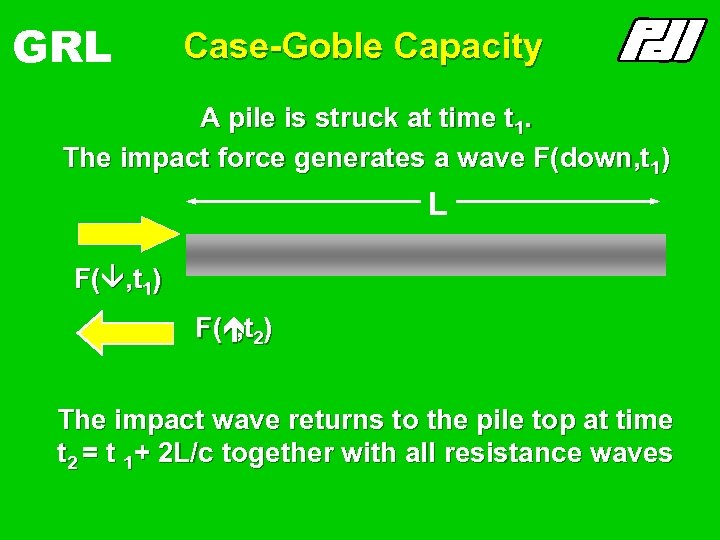GRL Case-Goble Capacity A pile is struck at time t 1. The impact force generates a wave F(down, t 1) L F( , t 1) F(ét 2) , The impact wave returns to the pile top at time t 2 = t 1+ 2 L/c together with all resistance waves

GRL The Case Method Equation At time t 2 = t 1 + 2 L/c the upward traveling waves arriving at the pile top include the reflection of the initial impact wave plus the sum of all resistances: F(ét 2) = - F( , t 1) + Ré , Or, rearranging we solve for the resistance: R = (F 2 -v 2 Z)/2 + (F 1 +v 1 Z)/2 where R is the total pile resistance, mobilized at a time L/c after t 1.

GRL The Case Method Equation R = ½(F 1 + Zv 1 + F 2 - Zv 2) F 1 and v 1 are pile top force and velocity at time 1 F 2 and v 2 are pile top force and velocity at time 2 Time 2 is 2 L/c after Time 1: t 2 = t 1 + 2 L/c R is the total pile resistance present at the time of the test, and mobilized by the hammer impact.

GRL Case-Goble Static Resistance Total Resistance = Static + Dynamic Rstatic= R - Rdynamic Need to estimate Rdynamic (Estimate it from pile velocity) Jc = ? SI US

GRL Case Damping Factor • To calculate static from total resistance, a viscous damping parameter, Jv , is introduced Rd = J v v • Non-dimensionalization leads to the Case Damping Factor, Jc: Jc = J v Z Rd = J c Z v Jc = ?

GRL Case-Goble Static Resistance Total Resistance = Static + Dynamic Rstatic= R - Rdynamic Rs = (1 -Jc)[F 1+ Zv 1]/2 + (1+Jc)[F 2 - Zv 2]/2 Jc = ? SI US

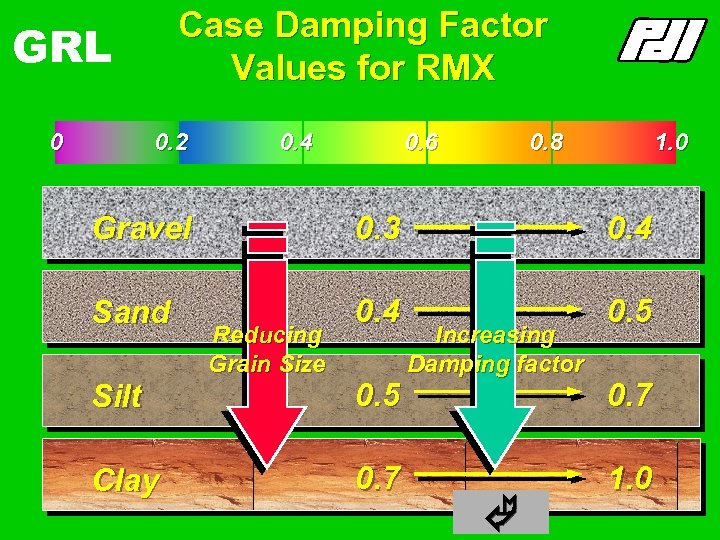Case Damping Factor Values for RMX GRL 0 0. 2 0. 4 0. 6 0. 8 1. 0 Gravel 0. 3 0. 4 Sand 0. 4 0. 5 Silt Clay Red u ci n g Grain Size 0. 5 0. 7 I n creasi n g D a m p i n g fa c to r 0. 7 1. 0

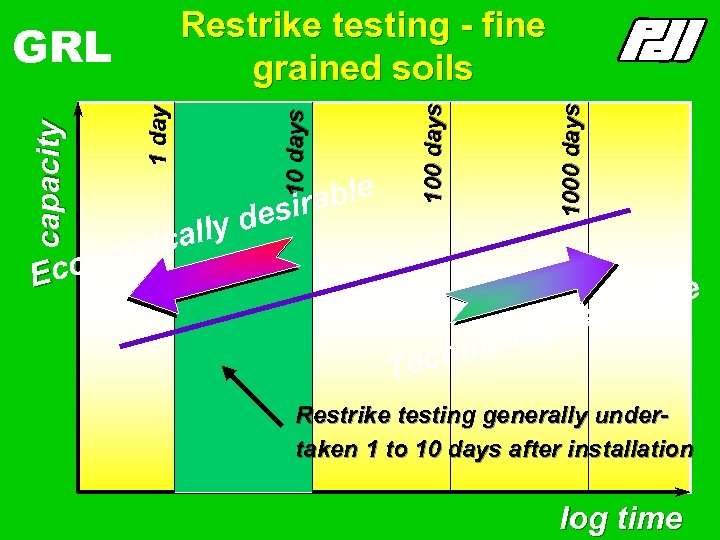able esir nom Eco lly d ica 1000 days 1 day capacity GRL 100 days Restrike testing - fine grained soils able esir lly d nica ech T Restrike testing generally undertaken 1 to 10 days after installation log time

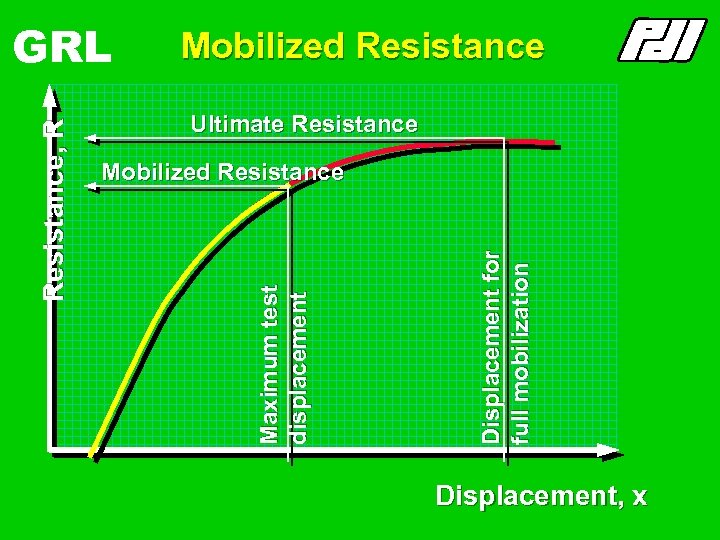Mobilized Resistance Ultimate Resistance Displacement for full mobilization Mobilized Resistance Maximum test displacement Resistance, R GRL Displacement, x

GRL Resistance: Rules for good correlation • Need to Mobilize Capacity (sufficient set per blow) • Account for time dependent strength changes Setup - Capacity increase Relaxation - Capacity decrease Therefore, restrike test pile after sufficient wait using a sufficiently large impact weight

GRL Capacity Results • GRLWEAP • by numerical analysis of assumed pile/hammer/soil prior to installation • Case Method • measured by PDA during installation • CAPWAP • by numerical analysis of measured PDA data after installation

GRL The Pile Driving Analyzer calculates. . .

GRL … PDA Results • Case Method Bearing Capacity • Pile Stresses • Compressive at Top • Bending at Top • Tension Below Top • Compressive at Bottom • Pile Integrity (Beta) • Transferred Energy

GRL PDA RESULTS vs GRLWEAP • CAPACITY – PDA: from force and velocity records – GRLWEAP: from analysis and blow count • TOP STRESSES – PDA: directly measured – GRLWEAP: from analysis and blow count • Note: Max. Compressive Stress does NOT always occur at Pile Top