Graph Drawing past — present — future Prof

Graph Drawing past - present - future Prof. Dr. Franz J. Brandenburg University of Passau Oct. 2002 1

Summary • past = standard algorithms = before 1990 – fundamental algorithms • • Reingold-Tilford for trees Sugiyama for DAGs (acyclic) spring embedders for general graphs Tutte embeddings for planar graphs • present = advances = 1990 - 2000 – improved versions – upwards planarity • future = todo = 2001 - 2015 – new and actual directions – open problems 2

Literature G. Di. Battista, P. Eades, R. Tamassia, I. G. Tollis Draph Drawing, Prentice Hall, 1999 M. Kaufmann, D. Wagner (eds). Drawing Graphs: Methods and Models LNCS 2025, Springer Verlag, 2001 Proceedings Graph Drawing Symposia, 1994 - 2001 LNCS 894, 1027, 1190, 1353, 1547, 1731, 1984, 2265 Journals JGAA, Comput. Geometry, Int. J. Comput Geom Appl, TCS, . . . G. Di. Battista, P. Eades, R. Tamassia, I. G. Tollis Algorithms for Drawing Graphs. an annotated bibliography Comp. Geom. Theory Appl. 4, 1994 "A Survey of Graph Layout Problems“ ACM Computing Surveys, Vol 34, 2002, 313 -356 3

History • Aristoteles (-384 - -322) noli turbare circulos meos • L. Euler (1707 -1783) Königsberg bridge problem planar graphs • E. Steinitz (1871 - 1928) planar graphs (polyhedrons, drawn by hand) • H. W. Tutte (1963) convex drawings of planar graphs • D. E. Knuth (1970) "How shall we draw a tree“ Special Reference: Kruja, Marks, Blair, Waters, GD 2001 4

What is Graph Drawing • mapping d : G ---> d(G) into R 2 (or R 3) a transformation from topology to geometry assign coordinates to the nodes and the bends of edges – placement of nodes – routing of edges v ---> (X(v), Y(v)) e ---> polyline • graph embedding into the grids – map nodes into grid points – route edges as paths along grid lines • cost measures for quality – area, edge length, crossings, bends, congestion, dilation, . . . • topology ---> shape ---> (geo)metric approach – identify graphs up to topology / shape / geometry isomorphism, including faces, translation & rotation 5

Classifications for Drawings • trees • ordered trees hierarchical radial • embeddings on the grid (H-, upwards, hv) • other techniques (organigrams, inclusion diagrams) • acyclic graphs, DAGs • Sugiyama algorithm • general graphs • force directed approaches • multi-dimensional approach • planar graphs • straight line (FPP) • orthogonal (Tamassia‘s flow technique) • visibility • other • two stage approaches 6

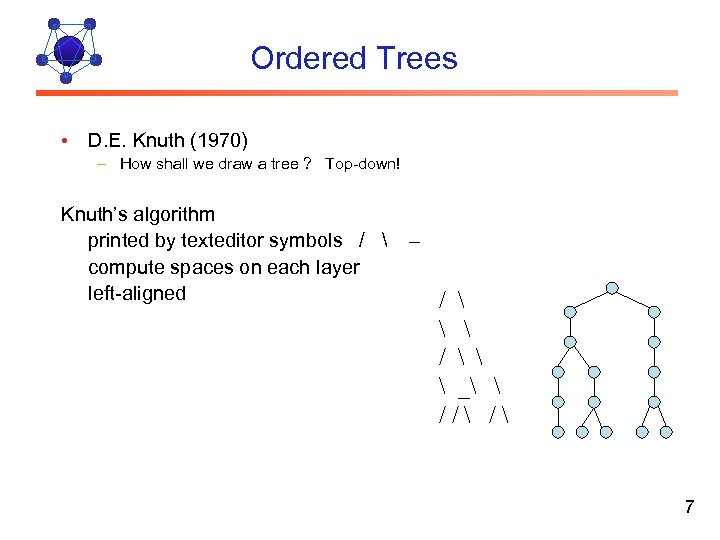Ordered Trees • D. E. Knuth (1970) – How shall we draw a tree ? Top-down! Knuth’s algorithm printed by texteditor symbols / compute spaces on each layer left-aligned – / / _ / / 7

Reingold-Tilford Algorithm (1) • Aesthetics – – – – horizontal by layer => Y-coordinate determined left-right ordering father centralized over its sons planar isomorphic subtrees are displayed isomorphic minimal horizontal distance integer coordinates (grid) • Implementation – – bottom-up in postorder compute the right-contour of Tleft and the left-contour of Tright compute minimal shifts for Tleft and Tright place the father above Tleft and Tright • O(n) – by lazy evaluation and offset computation 8

Reingold-Tilford Algorithm (2) • O(n) by – cost(T) = cost(T 1) + cost(T 2) + min{height(T 1), height(T 2)} = size(T) – height(T) • quality – symmetry and isomorphism: for free – in practice: OK – in theory: bad: O(n 2) area and too wide by (l l r)* • NP-hard for minimal width/area – grid + symmetry + center (Supowit-Reingold, Acta Inf. 1983) no e-approximation (1/24) – grid + ternary + center (Edler, Passau 98) 9

Reingold-Tilford Algorithm (3) • advanced features = many parameters – – – – arbitrary degree (Walker’s algorithm) arbitrary nodes sizes (width, height) leveling: global or local for each subtree (distances) father: center, median (innermost, outermost children) grid (integrality) edge anchors routing: straight-line, orthogonal, bus-layout my conclusion: ordered tree drawing is solved! Graphlet 10

Radial Tree Drawings • applications – block-tree of 2 -connected components – (minimal) spanning trees – telekommunication structures • radial algorithm by P. Eades – – – place nodes on concentric circles by level partition the circle into sectors of width „number of leaves“ draw the subtrees into their sectors the order is preserved planarity is not guaranteed • Graphlet – global and local leveling 11

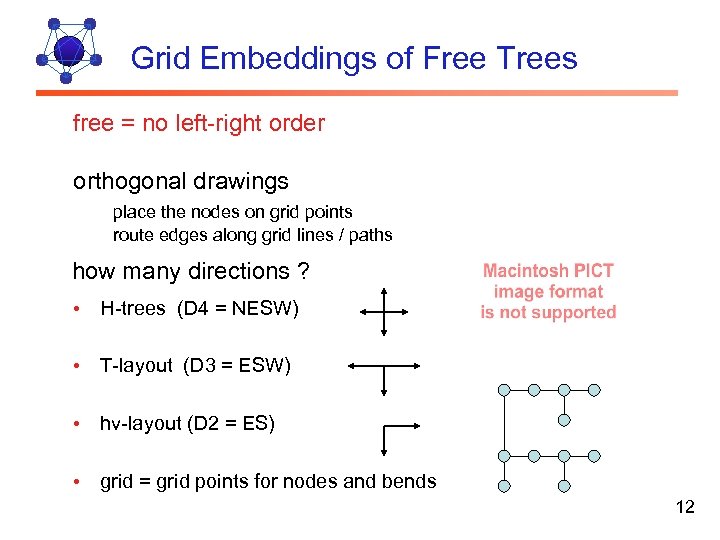Grid Embeddings of Free Trees free = no left-right order orthogonal drawings place the nodes on grid points route edges along grid lines / paths how many directions ? • H-trees (D 4 = NESW) • T-layout (D 3 = ESW) • hv-layout (D 2 = ES) • grid = grid points for nodes and bends 12

Complete Binary Trees • H-tree layout – area (n), since side-length(4 n) = 2 • side-length(2 n) – edge length ( ) with hyper-H-layout • T-layout (upwards) – „nothing new“ • hv-layout – area (n) for complete (balanced) trees – area (n logn) for arbitrary trees with width ≤ logn by h- and v- compositions 13

Hierarchical Drawings, Sugiyama • directed acyclic graphs, DAGs K. Sugiyama, S. Tagawa, and M. Toda IEEE Trans SCM 1981 (1) break cycles (2) compute layering, the Y-coordinates and insert dummy nodes for long-span edges (3) crossing reduction repeat down phase: sort next layer placement on lower layer up phase: sort previous layer placement on upper layer until DONE (4) routing of the edges 14

Force Directed Methods idea: a spring model select optimal edge length (node distance) k repeat for each node v do for each pair of nodes (u, v) compute repulsive force fr(u, v) = - c • for each edge e = (u, v) compute attractive force fa(u, v) = c • sum all force vectors F(v) = ∑ fr(u, v) + ∑ fa(u, v) move node v according to F(v) until DONE 15

Tutte’s Barycenter Algorithm G is planar and tri-connected (mesh of a convex polytope) drawing(G) is planar, straight-line, convex in O(n logn) Algorithm: select an outer face F = (v 1, . . . , vk) draw F convex e. g. as a k-gon fix the X- and Y- coordinates of F by d(vi) = (xi, yi), 1≤i≤k place each node v at the barycenter of its neighbours compute n n matrix A A[u, v] = 1/deg(v) for each edge e=(u, v) A[v, v] = -1 and A[vi, vi] = xi (resp. yi) and solve Ax = 0 (Ay = 0) Correctness and Complexity: Ax = 0 (resp. Ay= 0) has a unique solution (by Tutte) Ax = 0 is solvable in O(n logn) by specialized Gauss method 16

Drawing Styles • polyline drawings reduce bends, no sharp angles, polish by with Bezier splines • straight-line uniform (short) edge length • orthogonal drawings minimize bends • planar drawings minimize crossings and bends • grid embeddings grid coordinates for nodes and bend-points • visibility horizontal bar nodes and vertical visibility 17

Aesthetics (1) • • What is a nice drawing ? What makes drawings understandable or readable? How can we measure quality? Can we formalize aesthetics ? • Chinese proverb ”A picture is worth a thousand words“ • R. Feynman (Nobel prize in Physics) ”It’s all visual“ • R. A. Earnshaw (a poineer in computer graphics, 1973) ”visualization uses interactive compute graphics to help provide insight on complicated problems, models or systems“. ”Scientific visualization is exploring data and information graphically, gaining understanding and insights into the data“ • R. Hamming (1973) "the purpose of computing is insight not numbers" 18

Aesthetics (2) • recognize complex situations faster learn things more easily (sketch of a proof) – H. Purchase with students experiments on graph drawings (GD 97) • chess players recognize patterns • recognize graph properties – a path between two nodes – connectivity – Hamilton cycle (on the outer face) – interactive graph drawing competition (GD 2003) 19

Aesthetics (3) D. E. Knuth (GD' 1996) • ”Graph drawing is the best possible field I can think of: It merges aesthetics, mathematical beauty and wonderful algorithms. It therefore provides a harmonic balance between the left and right brain parts. “ • “A good graph drawing algorithm should leave something for the user‘s satisfaction. ” No perfect algorithm! R. Tamassia (IEEE SMC 1988, p. 62) • aesthetics are criteria for graphical aspects of readability 20

Aesthetic Criteria • visual complexity how long does it take to ”see everything“, to get the overview • regularity repetitions, fractals • symmetry geometric symmetry by rotation, reflection, translation • consistence coincidence of the picture and the intended meaning • form, size and proportionality • common drawing styles e. g. biochemical pathways, organigrams, ER-diagrams, • algorithmic efficiency seconds, not hours/years 21

Aesthetics Formalized • resolution or geometric criteria – – – area (2), volume (3 D), height, width, aspect ratio edge length (sum, max, all uniform (Hartfield&Ringel, Pearls. . )) angular resolution (avoid small angles) uniform node distribution integrality, grid drawings/embeddings • • all nodes and bends of polylines all nodes and edges (grid embedding) sizes of all faces (Hartfield&Ringel, Pearls in Graph Theory) 22

Aesthetics Formalized • discrete criteria – – – crossings bends load factor (overlaps of nodes) congestion (parallel edges) edit complexity (insertions, deletions, moves) • symmetry – center father above the children – geometric symmetry (rotation, reflection) – graph symmetry, graph isomorphy • constraints – Sesame street relations (left-right, top-down) – place distinguished nodes (e. g. center, at the border) – clustering 23

Formalization an information theoretic approach to aesthetics Max Bense, designer at Bauhouse school (1930) aesthetics = order complexity redundancy information ”nice“ order complexity = redundancy information = regularity = descriptional complexity, bit representation = log n – H(∑) = information content if well-ordered, symmetric if high redundancy, not overloaded, not compressed 24

Aesthetics = Optimization • MIN {cost(d(G)) | d(G) is feasible} cost measures the aesthetic criteria feasible guarantees no overlaps etc • most important fulfill the common standards (hierarchical, planar, left-right; bio-informatics) • be ”almost“ optimal do not waste space, but do not minimize the area • "aesthetics cannot be formalized“ there is a gap between the user's view and the formalism D. E. Knuth (Graph Drawing '96) 25

References Aesthetics G. Nees, Formel, Farbe, Form Computerästhetik für Medien und Design. Springer (1995) H. W. Franke Computergraphik - Computerkunst (1971) R. Tamassia, G. Di Battista, C, Batini "Automatic graph drawing and readability of diagrams“, IEEE SMC 18 (1988), 61 -79 C. Batini, E. Nardelli, R. Tamassia "A layout algorithm for data flow diagrams“, IEEE-SE 12 (1986), 538 -546 C. Kosak, J. Marks, S. Shieber, "Automating the layout of network diagrams with specific visual organization", IEEE-SMC 24 (1994), 440 -454 H. C. Purchase, R. Cohen, and M. James "Validating graph drawing aesthetics“, Proc. GD'95, LNCS 1027 (1996), 435 -446 C. Ding, P. Mateti "A framework for the automated drawing of data structure diagrams" IEEE SE-16 (1990), 543 -557 J. Manning "Computational complexity of geometric symmetry detection in graphs“. LNCS 597 (1991), 1 -7 J. Manning, M. J. Atallah "Fast detection and display of symmetry in outerplanar graphs" Disc. Appl. Math. 39 (1992), 13 -35. 26

present 1990 -2000 theoretical foundations, extensions, improvements Graph Drawing Symposia ’ 93 – ’ 02 27

Trees • ordered trees solved Reingold-Tilford algorithm with extensions radial drawings • free trees something TODO preserve planarity swap left-right subtrees to minimize the area --> NP ? – complete trees solved H-trees in O(n) area hv-trees in O(n) area – arbitrary trees next 28

Exact Bounds are NP-hard • H-tree Bhatt-Cosmadakis reduction of Not. All. Equal 3 SAT area(T) ≤ w • h iff width(T) ≤ w iff NEA 3 SAT edge-length = 1 iff NEA 3 SAT 29

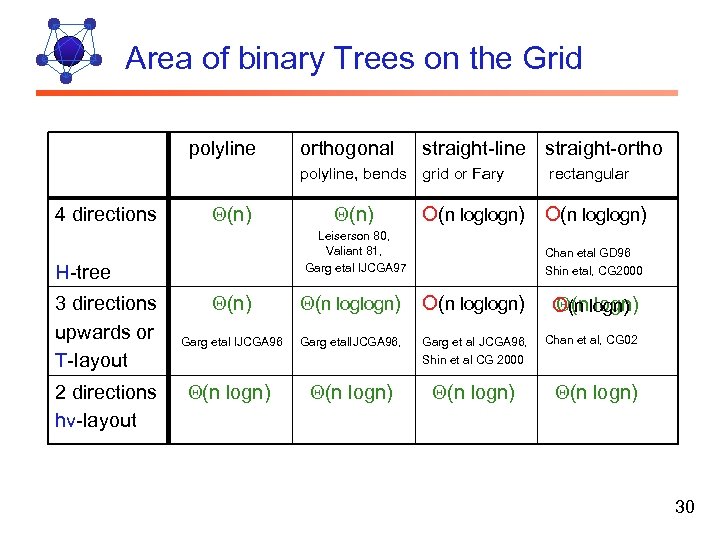Area of binary Trees on the Grid polyline orthogonal straight-line straight-ortho polyline, bends grid or Fary 4 directions (n) 2 directions hv-layout O(n loglogn) Leiserson 80, Valiant 81, Garg etal IJCGA 97 H-tree 3 directions upwards or T-layout (n) rectangular O(n loglogn) Chan etal GD 96 Shin etal, CG 2000 (n) (n loglogn) O(n loglogn) (n logn) O(n logn) Garg etal IJCGA 96 Garg etal. IJCGA 96, Garg et a. I JCGA 96, Shin et al CG 2000 Chan et al, CG 02 (n logn) 30

the lower bound with Given Width choose an arbitrary width, e. g. W = √n or W = log n consider the following tree T T = a chain of length n/2 W and a complete binary tree of site W/2 at each W‘s node of the chain. These nodes are called T-joins. CLAIM 1 Each complete tree of size k needs k in each dimension (height, width) CLAIM 2 Each rectangle of width W-1 and height (log. W)/2 has at most one T-join THEN area(T) ≥ W * (n/W)*log. W) = n*log W which is Ω(n logn) for W = n a T-join W-1 nodes „waiste height“ n/2 nodes in n/2 W lines complete tree of size W/2 log n/2 W complete tree of size W/2 31

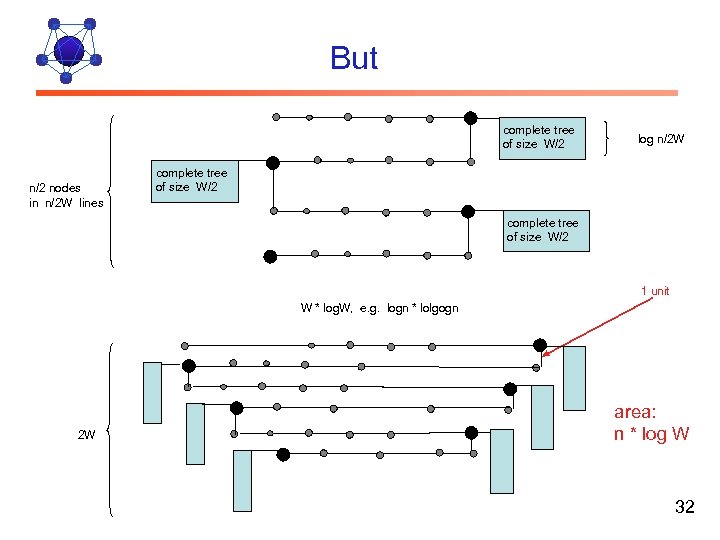But complete tree of size W/2 nodes in n/2 W lines log n/2 W complete tree of size W/2 1 unit W * log. W, e. g. logn * lolgogn 2 W area: n * log W 32

Tree Folding O(n) area for complete tree with width 8 = √ 64 33

Techniques • make trees left-heavy |Tleft| ≥ |Tright| a weaker version of balance with right-depth(T) ≤ logn • recursive winding partition in subtrees of appropriate sizes and merge • solve complex recursion formulas References: T. Chan, M. Goodrich, S. R. Kosaraju, R. Tamassia, Comput. Geom. 23 (2002) A. Garg, M. Goodrich, R. Tamassia, Int. J. Comput. Geom. Appl. 6 (1996) C. Shin, S. K. Kim K-Y. Chwa, Comput Geom. 15 (2000) 34

other Tree Drawing Conventions • standard Knuth ”how shall we draw a tree“ Reingold-Tilford algorithm • MS-file system special hv-drawings • tip-over = horizontal+vertical tip overs • inclusion diagrams – minimal size = NP-hard by PARTITION 35

OPEN Problems on Trees • H-tree layouts – area of straight-line and straight-orthogonal drawings, O(n loglogn) – sum of edge lengths O(n logloglog n) (Shin et al. IPL 1998) – bends • T-tree layouts (upwards) – area of straight-orthogonal drawings (in Chan et al CG 23 (2002)) my CLAIM: O(n loglogn 2) area by twisted windings Correction 9. 10. 02 • hv-layouts – which trees (weak balance) have area O(n) ? • better aspect ratio (width / height = 1) – often: n/ logn – Wanted: arbitrary • exact bounds for T and hv layouts: are they NP-hard? 36

Advanced Sugiyama • synonyms: hierarchical = DAG-layouts = Sugiyma style • aesthetics and conventions – – edges point downwards long edges should be avoided, i. e. few dummy nodes few edge crossings many straight (vertical) edges • the algorithm – (1) compute layering – (2) crossing reductions – (3) routing with few bends • extensions 37

Phase 1: Remove Cycles feedback arc set problem is NP-hard (Karp 72) minimize the number of „to be deleted“ edges Ed minimize the number of „to be reversed“ edges Er maximal acyclic subgraph by Ea = E – Ed Lemma reverse each „deleted“ edge Er = Ed heuristics (see Bastert, Matuszewski in LNCS 2025) • depth-first search (or bfs) and reverse each „backedge“ • problem specific (while-loops, return-jumps, known cycles (acid cycle)) • in-out degree dominance deleting at most m/2 – n/6 edges (Eades et al. 1993) reverse topsort from the sinks topsort from the sources sort nodes v by outdegree(v) – indegree(v) keep the outgoing edges (v, w) and delete the incoming edges (u, v) exact methods by LP-methods and the LP polytopes 38

Phase 2: Layering layer span (v) = interval of layers on which v can be placed dummy nodes = nodes on intermediate layers • topological sorting ASAP ALAP computes minimal height layering in O(n+m), min height is solved! • Coffman-Graham method (multi-processor scheduling) sort the nodes by their maximal distance from the sources bottom-up assign at most k nodes to each layer by choosing the largest node whose descendants have already been placed => computes layering of width ≤W and height ≤ (2– 2/W) • heightmin • ILP algorithm of Ganser etal. (1993) minimize #dummy nodes min{Y(u) – Y(v)-1) | e=(u, v) } is polynomially solvable gives the ”best“ practical performance • minimal width is NP-hard (Branke etal IPL 02, and scheduling theory) 39

Phase 3: Crossing Minimization algorithm: layer by layer sweep iterative improvement (finitely many rounds) theory: two-layer crossing minimization is NP-hard ILP-formulation and branch and cut works well up to 60 nodes method: repeat in down and up phases sort next layer by barycenter or median works well and efficient in practice Who needs something better ? OPEN global crossing minimization, over all layers 40

Phase 4: Coordinate Assignment all dummy nodes of a path p should lie on a straight line the deviation is minimized dev(p) = ∑ (x(vi) – (vi))2 with (vi) at most two bends for each long span edge and strict vertical between the bends integrate into the crossing minimization using heavy weights for dummy vertices and using exstra space (Sander, TCS 2000, Gansner etal) 41

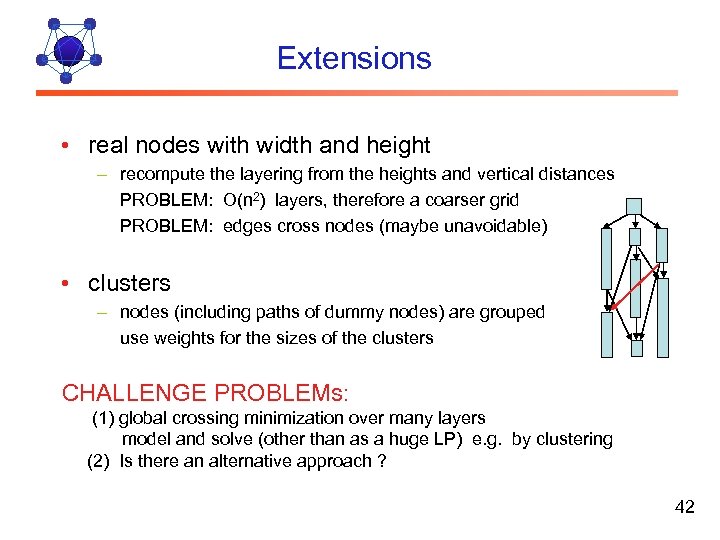Extensions • real nodes with width and height – recompute the layering from the heights and vertical distances PROBLEM: O(n 2) layers, therefore a coarser grid PROBLEM: edges cross nodes (maybe unavoidable) • clusters – nodes (including paths of dummy nodes) are grouped use weights for the sizes of the clusters CHALLENGE PROBLEMs: (1) global crossing minimization over many layers model and solve (other than as a huge LP) e. g. by clustering (2) Is there an alternative approach ? 42

General Graphs • force directed methods – in a loop compute attractive and repulsive forces and move the nodes according to the force-vectors • good: – intuitive concept – easily adaptable and extensible (more forces) • bad: – – – running time termination which forces too many parameters: the best selection and default values a „bag“ of tricks 43

Forces • attractive forces – along each edge – proportional to shortest paths • repulsive forces – between each pair of nodes (O(n 2) pairs, costly!) – only between closely related nodes (hash grid) • other forces – – center of gravity (attractive) underlying magnetic fields (concentric, radial, horizontal) angular forces (between adjacent edges at nodes v) from the boundary (repulsive; bounce back) 44

Strength of Forces • k = an ideal distance between nodes the ideal edge length k, k = 0. 75 • • forces –linear (Hooks’s law) –logarithmic (Eades, 1984) –quadratic, p=2 (Fruchterman, Reingold 90) –cubic, p=3 (Forster, 99) • formula not good in practice too costly, too severe standard faster to compute, no (p=2, 3) fattract(u, v) = – frepulsive(u, v) = ideal distance iff fattract(u, v) + frepulsive(u, v) = 0 45

Spring Embedder choose k, the ideal distance compute an initial placement (at random, by user) repeat for each node v do compute force vector (v) move v, d(v) = d(v) + d • (v) until DONE loop: – finitely many iterations – cooling schedule, the temperature d decreases geometrically by 0. 95 i – oszillations, vibrations, rotations by lower temperature 46

Energy Model repeat compute the global energy (sum of all forces) for all nodes (in some order) do check movement of the node by d if improvement or random, then execute movement decrease the temperature until DONE Kamada-Kawai quadratic forces / energy all pairs of nodes and shortest distance (paths) move the currently best node (compute minimum at zero derivative) good in symmetry, particilarly on polyhedra 47

Experience Force Directed Methods are • good quality on many graphs • always slow • many modifications – – – forces cooling schedule for termination restrict oszillations, vibrations, rotations adaptations of simulated annealing, TABU methods etc. randomized versions (Tunkelang) • a ”bag of tricks“ (too many parameter) OVERALL: they are GOOD 48

Multi-Dimensional a promising new concept by D. Harel and Y. Koren, GD 2002 choose dimension m, e. g. d = 50 choose m nodes as pivot elements, randomly distributed here in O(d • |E|) by BFS v 1 at random and vi+1 = max {distance{v 1, . . . , vi}} (2 -approximation of d-center problem) for each node v compute its graph theoretic distance d(v, vi), i=1, . . . , d to the pivot nodes and assign an d-dim vector X(v) = (d(v, v 1), . . . , d(v, vd)) This is a d-dimensional drawing of G. 49

Multi-Dimensional(2) projection into R 2 (or R 3) by ”principal component analysis“ transform the coordinates in each dimension around their barycenter Xi(v) = Xi(v) – 1/n∑v. Xi(v) construct the d n center matrix M[i, v] = Xi(v) construct the d d covariance matrix S = 1/n MMT compute the first 2 eigenvectors of S normalize the eigenvectors to ||ui || = 1 the 2 -D projection by v --> (Xi(v) u 1, Xi(v) u 2) (maximal variance in 1 st and 2 nd dimension) Results: excellent pictures extremely fast, 3 sec. for 100000 node graphs 50

Planar Graphs • O(n) recognition algorithms – path addition method (Hopcroft, Tarjan, 1973) – node addition method (Lempel, Even, Cederbaum, 1967) with witness by a Kuratowski graph • Tutte’s barycenter method – place outer face on a convex face, e. g. n-gon – place inner nodes at the barycenter of their neighbours – solve Ax=0 (by special techniques in O(n logn)) only for tri-connected planar graphs convex inner faces ”bad“ drawings low angular resolution (too many small angles) clustering 51

Planar Fary Embeddings • FPP algorithm (de. Fraisseix, Pach, Pollak, 1989) – compute a canonical ordering, a peeling of G – initialize: a triangle – iteration: add vk+1 at a grid point and above its lower neighbours shift the nodes below vk+1 by +1 shift the nodes right of vk+1 by +2 This guarantees even Manhatten distance! Save the shifts in an offset tree for O(n) time. – area: (2 n-4) (n-2) with improvement to (n-2) 52

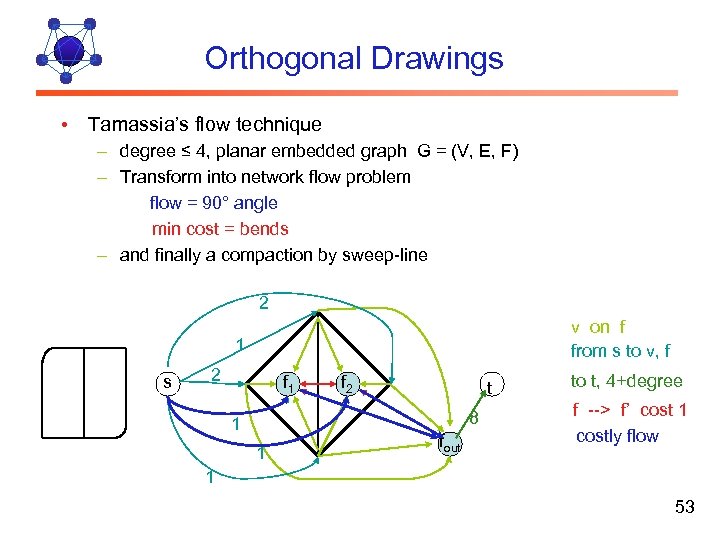Orthogonal Drawings • Tamassia’s flow technique – degree ≤ 4, planar embedded graph G = (V, E, F) – Transform into network flow problem flow = 90° angle min cost = bends – and finally a compaction by sweep-line 2 v on f from s to v, f 1 s 2 f 1 f 2 t 8 1 1 fout to t, 4+degree f --> f’ cost 1 costly flow 1 53

Orthogonal • Kandinski approach extension to higher degree and parallel edges based on Tamassia’s flow technique Fößmeier, Kaufmann, GD 95 -97 • incremental approach add next node with open columns based on canonical ordering Biedl et al. GD 95 -98 • visibility compute st-numbering for G and G* (dual graph) and assign coordinates to bar-nodes Tamassia&Tollis (86), Rosenstiehl&Tarjan (86), Wismath (87) 54

Planar Drawings there is no ”perfect, nice“ algorithm, yet • good: – O(n 2) area – O(n) time • bad: – no uniform node distribution – many bends (orthogonal) and small angles • best compromise – orthogonal drawings (Kandinski model) – mixed model (Kant‘s variation) 55

future 2000 ---> new developents actual challenges OPEN problems 56

Huge Graphs • huge = to large to fit onto the screen e. g. 200 or more nodes (software systems) techniques fisheye mode reduce the resolution towards the boundary to zero hide information browse into the graph for more details 57

try 3 -D Graph Drawing • each graph has a straight-line 3 -D drawing with O(n 3) volume vi ––> (i, i 2, i 3) mod p, n < p < 2 n and p prime momentum curve, Vandermond matrix • folding graphs in 3 D with few bends orthogonal => degree ≤ 6 volume ≤ O( ) O( bends ≤ 7 lower bound: bends ≥ 2 m + 6/7 n ) (Eades, Symvonis, Whitesides, GD 96) (Wood, GD 2000) 58

Preprocessing STATEMENT All practical algorithms need & have a preprocessing phase priority among properties and aesthetics • (1) classification general, DAG, planar, tree, . . • (2) by connectivity – connected components: treat them separately • problems: e. g. spring embedders, only repulsive forces – bi-connectivity is „hard“, • computable in O(n) by extended DFS, compute (north-south) pole-pairs • often a pre-supposition, e. g. planarity test • add edges for bi-connectivity • (3) What else? OPEN 59

Clustered Graphs • clustered graphs and c-planarity (Feng, Eades, LNCS 959, 979, . . ) – C = (G, T) = (graph G + tree T) nodes of G = leaves of T inner nodes of T = tree-like nested subsets of nodes edges are inside in the next higher region and at most one edge-region crossing per edge • applications – tree structure = new level of abstraction = clustering of G (supernodes and browsing) 60

Drawing Clustered Graphs • drawings the underlying graph G is drawn – planar orthogonal or straight line or – G is acyclic and is draw in Sugiyama style tree = inclusion tree diagram regions are drawn as convex boxes in O(n 2) time needs up to exponential area for straight-line planarity multi-level = tree in 3 D a pyramide • preserve the mental map while browsing 61

Clustered Graphs • recognition – Each c-planar graph is a subgraph of a connected c-planar graph – O(n 2) algorithm for c-planarity with embedding or if all clusters are connected OPEN: a challenge problem Is G c-planar? Connectivity or an embedding makes it! (guess: NP-hard) OPEN: Given G. How to find T? 62

Compound Graphs • compound graphs (Sugiyama, Misue, IEEE Trans SCM 21 (1991)) (G+T+I) = graph + tree + inner-tree edges G directed, acyclic T represented by rectangular boxes I lines connecting the boxes drawing G in Sugiyama style T as regions • state charts (Harel, C ACM 88) (G + D) = graph + dag drawing no complete concept, hide some information 63

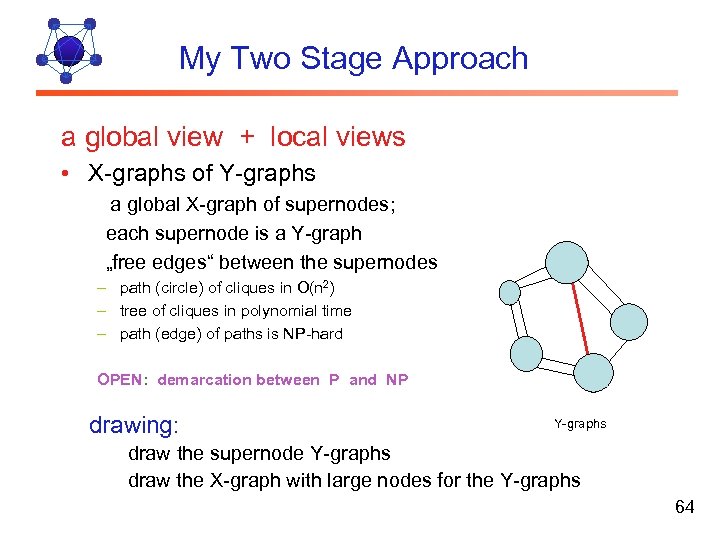My Two Stage Approach a global view + local views • X-graphs of Y-graphs a global X-graph of supernodes; each supernode is a Y-graph „free edges“ between the supernodes – path (circle) of cliques in O(n 2) – tree of cliques in polynomial time – path (edge) of paths is NP-hard OPEN: demarcation between P and NP drawing: Y-graphs draw the supernode Y-graphs draw the X-graph with large nodes for the Y-graphs 64

Clustering • how? – by the underlying meaning (cluster analysis in information systems) – by connectivity separators and cut methods partition algorithms (Fiduccia&Mattheyses, ratio cut) – by node degrees (Batagelj etal, GD 99) • What else? OPEN 65

Miscellaneous Areas • • • labelling of nodes and edges planar upwards drawings circular drawings symmetry and isomorphism proximity drawings (Gabiel graphs etc) dynamic graph drawing mental map declarative approaches (layout graph grammars) Tools and Systems Experimental Studies 66

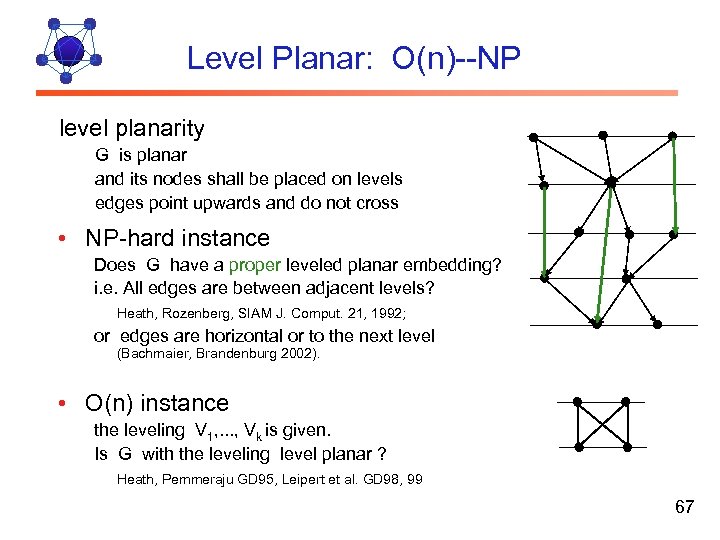Level Planar: O(n)--NP level planarity G is planar and its nodes shall be placed on levels edges point upwards and do not cross • NP-hard instance Does G have a proper leveled planar embedding? i. e. All edges are between adjacent levels? Heath, Rozenberg, SIAM J. Comput. 21, 1992; or edges are horizontal or to the next level (Bachmaier, Brandenburg 2002). • O(n) instance the leveling V 1, . . . , Vk is given. Is G with the leveling level planar ? Heath, Pemmeraju GD 95, Leipert et al. GD 98, 99 67

Upwards Planarity G is directed and planar Does G have a strictly upwards planar drawing i. e. all edges are strictly Y-monotonous polylines NP-hard (Garg Tamassia, SICOMP. 31, 2001) G has no triangles, then YES G tri-connected G an embedded planar graph G outerplanar O(n 6) O(n) O(n 2) (Kisielewicz, Rival, Order 1993) (Bertolazzi et al Algorithmica 1994) (Bertolazzi et al SICOMP 1998) (Papakostas, GD 94) OPEN G series-parallel or tree-with(G) ≤ 3 68

Rectlinear Planar G is undirected, planar Does G have a straight orthogonal drawing straight-orthogonal = rectlinear = H-layout NP-hard (Garg Tamassia, SICOMP 31, 2001) binary trees H-layout with Ω(n loglogn) area. Is this the lower bound? Recall: for T- and hv layout the bound is (n logn) OPEN • • minimal area for binary trees in T and hv layout (H is NP-hard) G outerplanar or series-parallel graphs Does G have a rectlinear layout? What is minimal area? 69

Special: Thickness thickness – planar –– geometric –– outerplanar (book-) –– forest –– tree how many layers of planar, . . . , trees are needed to cover all edges? – generall recognition: solved • NP-hard for planar (Mansfield 83), outerplanar (Widgerson 85), trees (Br) • polynomial forest (Nash-Williams, J. London Math. Soc 69) • OPEN for geometric (Eppstein et al. JGAA 4 (00), GD‘ 02) – exact thickness, for fixed k • k=1 • k=2 is easy O(n) NP for outerplanar and trees OPEN What graphs have small xyz-thickness numbers? e. g. rectlinear visibility (and |E| ≤ 3 k • |V|-18 k 70

Angles in Planar Drawings angular resolution π(G) a straight-line planar drawing the smallest angle between edges orthogonal = 90° angles 300 30 30 20 40 obvious: π(G) ≤ 360° / degree but π(K 3) = 60° π(K 4) = 30° π(square) = 90° 300 30 40 30 20 120 120 illegal undrawable 30 20 30 40 300 problems decide angle drawabiliy with given consistent angles all planar drawing algorithms have low angular resolution: Do better ! FPP: a ≤ 360°/ 2 n n=60, then 10% of the angles are less than 5° 71

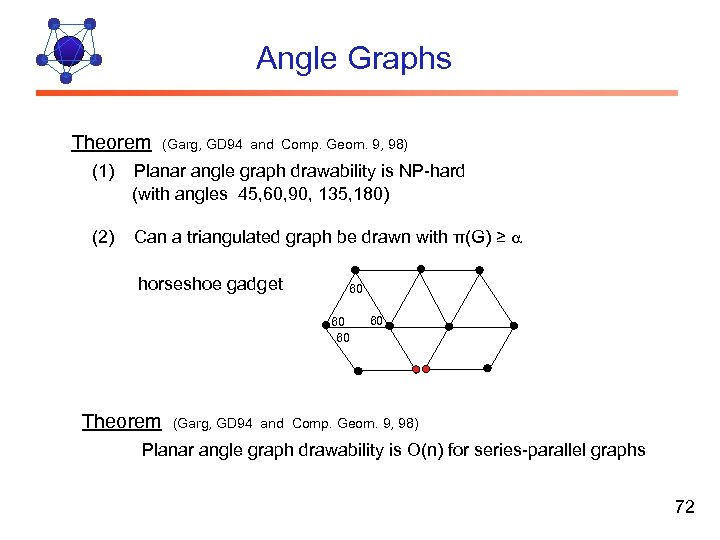Angle Graphs Theorem (Garg, GD 94 and Comp. Geom. 9, 98) (1) Planar angle graph drawability is NP-hard (with angles 45, 60, 90, 135, 180) (2) Can a triangulated graph be drawn with π(G) ≥ a horseshoe gadget 60 60 60 Theorem 60 (Garg, GD 94 and Comp. Geom. 9, 98) Planar angle graph drawability is O(n) for series-parallel graphs 72

Angle Constraints G is a planar embedded graph variables ai for each angle, 2 e variables the angles for each vertex v for each face vertex consistency face consistency ∑ ai = 360° ∑ ai = (k-2) • 180° ((k+2) • 180° for the outer face) Theorem (Di. Battista, Vismara, STOC 93) a triangulated planar graph G is drawable iff angle constraints and wheel condition at each v are satisfied wheel condition 1 a 2 5 a 1 a 5 4 a 4 3 2 a 3 73

the Angle LP max {a 0 | A a = b, ai ≥ 0, ai ≥ a 0} for each vertex v for each face vertex consistency face consistency ∑ ai = 360° ∑ ai = (k-2) • 180° ((k+2) • 180° for the outer face) for each angle nonnegative a lower bound ai ≥ 0 ai ≥ a 0 size of A 2 e angles ai (and a 0) v + f equations for vertices and faces e inequalities ai ≥ a 0 A is a (v+f+e) (2 e+1) = (2 e+2) (2 e+1) matrix but in normal form (ai ≥ a 0 => ai–si = a 0) there are e-1 more variables than equations (under-determined) 74

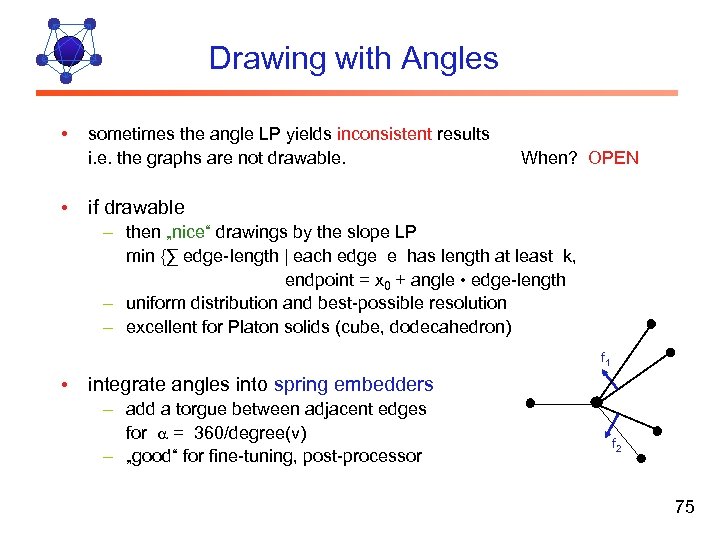Drawing with Angles • sometimes the angle LP yields inconsistent results i. e. the graphs are not drawable. When? OPEN • if drawable – then „nice“ drawings by the slope LP min {∑ edge-length | each edge e has length at least k, endpoint = x 0 + angle • edge-length – uniform distribution and best-possible resolution – excellent for Platon solids (cube, dodecahedron) f 1 • integrate angles into spring embedders – add a torgue between adjacent edges for a = 360/degree(v) – „good“ for fine-tuning, post-processor f 2 75

Orderings of Graphs traversing a graph and its impact – dfs • • – connectivity planarity test (Hopcroft-Tarjan path adition) bfs • • acyclic concentric representation of planar graphs; no „long“ edges – st numbering (or bi-polar orientation) • • planarity test (Even-Lempe-Cederbaum node addition) visitbility representation – canonical ordering of planar graphs • Fary embeddings of planar graphs (FPP) OPEN What is the best ordering (for a particular purpose) ? Orderings with property π, e. g. short longest path (depth) 76

New Direction: Partiality • ”almost“ π-graphs for some property π – almost planar (with few crossings) – almost acyclic (with few cycles, delete O(1) edges)) – an extension of G has property π, e. g. k-th power Gk • subgraph drawing – apply a drawing algorithm to a selected subgraph, only, and cluster • similarity – define “weaker versions“ of isomorphism • squeeze meshes, ”meshes are for free“ – analogy: tree-width of graphs, now „mesh-width“ 77

Premium Open Problems • Which planar graphs have O(n) area straight line drawings? O(n 2) for all (FPP) O(n) for trees, grids O(n log n) for outerplanar graphs (Biedl, GD 02) • What is the constant for planar straight-line drawings in O(n 2)? 4/9 ≤ c ≤ 1 Conjecture: 4/9, (from He GD 94, p. 287) Yes, exactly 4/9 for polyline drawings with ≤ 1 bend per edge (Bonichon, Le. Saic, Mosbah, WG 2002) 4 -connected convex with 4 -outerface on (n/2 n/2) (He, 97) this bound is optimal (Nishizeki et al, ISAAC 2000) proof via canonical ordering and fewer shifts by 4 -connectivity • volume of graphs (from Cohen, Eades, Lin, Ruskey, GD’ 94, p. 9) 3 -D straight-line drawings in O(n n n). Do better! 3 -D straight-line drawings of binary trees in O(n 1/3 ). Do better! 78

Premium Open Problems • Is c-planarity NP hard? • Global crossing minimization in Sugiyama style drawings • The lower bounds on area and bends for orthogonal drawings of nonplanar graphs (Papakostas, Tollis, GD’ 94, p. 50) • A ”good“ planar drawing algorithm with good distribution of the nodes (or arguments that this cannot exist) 79

More Open Problems • Characterize consistent planar angle graphs? (Br 02 generalizing Vijajan Proc. ACM CG 86, Garg, GD’ 94, p. 86. ) • Find an st-numbering of a planar graph that minimizes the length of the st-path ( He, Kao, GD’ 94, p. 101) • Design general graph drawing with real sized nodes Avoid node-edge crossings and provide a „good“ node distribution) • Which trees have a legal, non-crossing radial drawing by the Eades algorithm and can one make the Fruchterman-Reingold algorithm radial? 80

A Special Problem • multi-source shortest paths Application: Harel&Koren’s multidimensional approach PROBLEM: a graph G = (V, T) with |V|=n, |E|=m and a set of sources s 1, . . . , sd • all edges have unit length – Find the shortest paths from each source s to each other node v – in less than O(d • m) – GOAL: O(m + d • n) • non-neative costs (edge lengths) • GOAL: not d* Dijkstra but O(m + d • nlogn) • IDEA: • do BFS/Dijkstra‘s computation simultaneously for each source • and re-use earlier shortest paths trees from other sj 81

The END Thank you – for listening – asking very good questions – giving me a good feedback and new inspirations Please, solve many of the problems 82