Graph algorithms for compiler developers Alexander Ivchenko

Graph algorithms for compiler developers Alexander Ivchenko

Agenda • Small intro • Register allocation problem as the showcase • Other areas in the compiler where graphs help

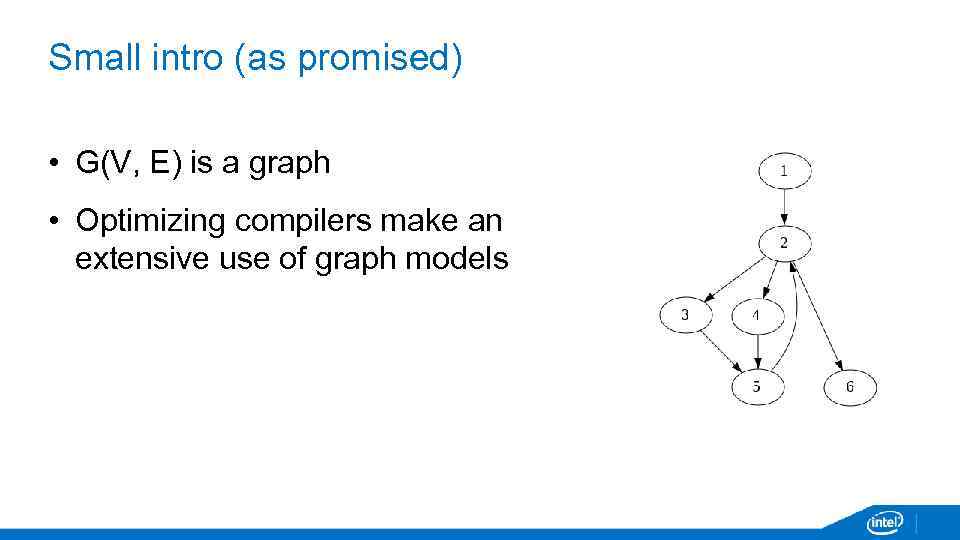Small intro (as promised) • G(V, E) is a graph • Optimizing compilers make an extensive use of graph models

Register allocation and Memory hierarchy • Programs are written as if there are only two kinds of memory: main memory and disk • Programmer is responsible for moving data from disk to memory (e. g. , file I/O) • Hardware is responsible for moving data between memory and caches • Compiler is responsible for moving data between memory and registers

Example of register allocation • Take a look at the program: a : = c + d e : = a + b f : = e – 1 • Assume that a and e are not used (this is called “dead”) after that code • How we should allocate those variables to physical registers? • Register that stores “a” variable can be reused after “e : = a + b” • Register that stores “e” variable can be reused after “f : = e – 1” • We can allocate “a”, “e” and “f” onto the same register (r 1) r 1 : = r 2 + r 3 r 1 : = r 1 + r 4 r 1 : = r 1 - 1

The idea behind register allocation • The value in a “dead” variable is not needed - we can reuse the register that was used for storing that value once the variable is dead • If two values are “live” simultaneously we cannot allocate them onto one register

Register interference graph We build the graph: • Nodes of interference graph are variables • Two nodes are connected if the corresponding variables are live simultaneously at some point in the program - This is interference graph (IG) We can allocate two variables onto the same register if there is no edge connecting the corresponding nodes in IG

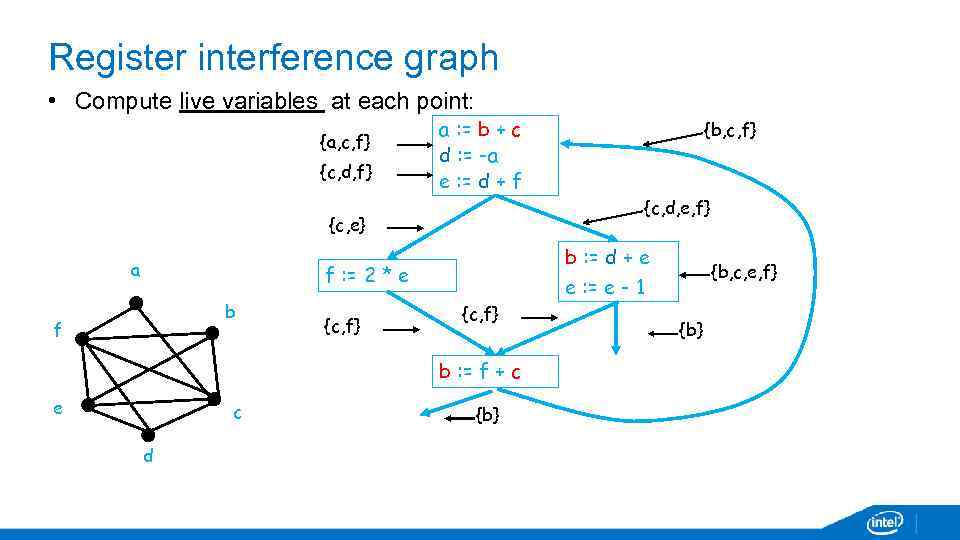Register interference graph • Compute live variables at each point: {a, c, f} {c, d, f} a : = b + c d : = -a e : = d + f {c, d, e, f} {c, e} a b : = d + e f : = 2 * e b f {c, f} c d {b, c, e, f} e : = e - 1 {c, f} b : = f + c e {b, c, f} {b}

Register allocation via graph coloring • A Graph Coloring is an assignment of colors to nodes of the graph, so that any two connected nodes have different colors • A graph is k-colorable if it has a coloring with k colors In our case colors = registers

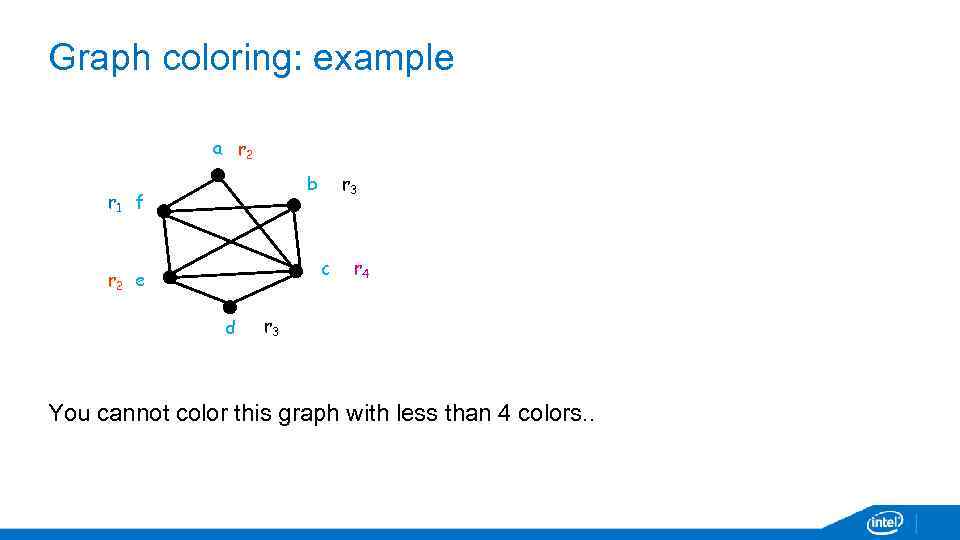Graph coloring: example a r 2 r 3 b r 1 f c r 2 e d r 4 r 3 You cannot color this graph with less than 4 colors. .

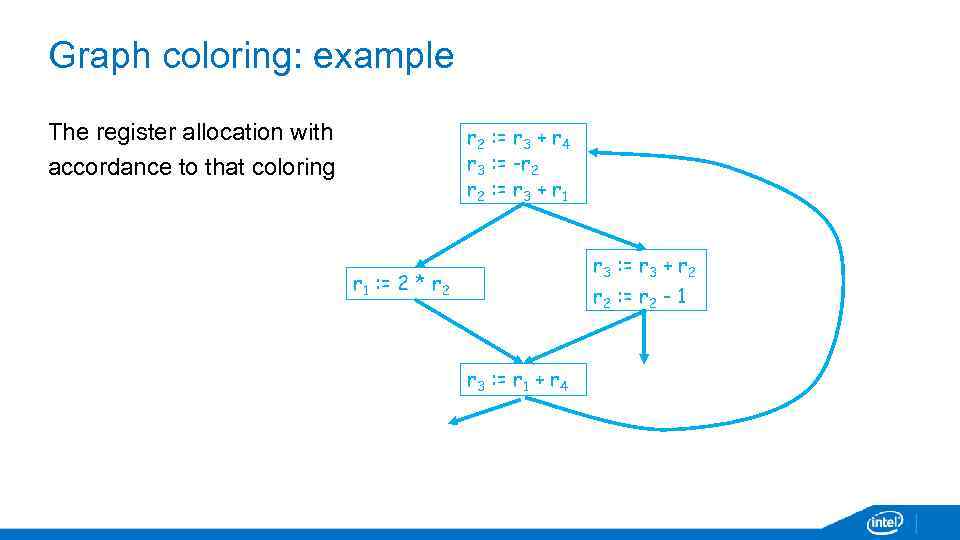Graph coloring: example The register allocation with accordance to that coloring r 2 : = r 3 + r 4 r 3 : = -r 2 : = r 3 + r 1 r 3 : = r 3 + r 2 r 1 : = 2 * r 2 : = r 2 - 1 r 3 : = r 1 + r 4

Register allocation via graph coloring • So we need to compute a coloring for IR, but • This is a NP-hard problem, which means we don’t have an exact efficient algorithm (so far) • Even if we find the minimal coloring for IR, we still can have less registers

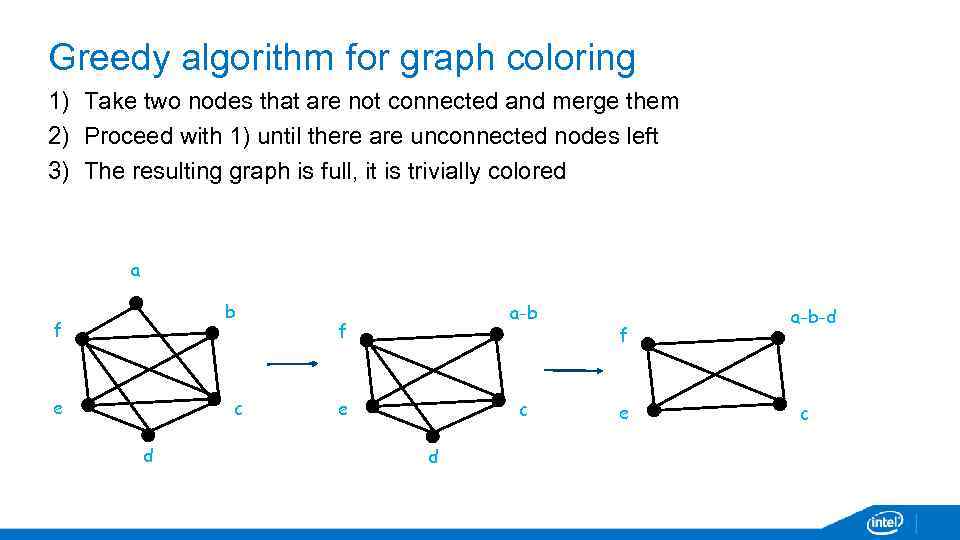Greedy algorithm for graph coloring 1) Take two nodes that are not connected and merge them 2) Proceed with 1) until there are unconnected nodes left 3) The resulting graph is full, it is trivially colored a b f e c d a-b f e c d f e a-b-d c

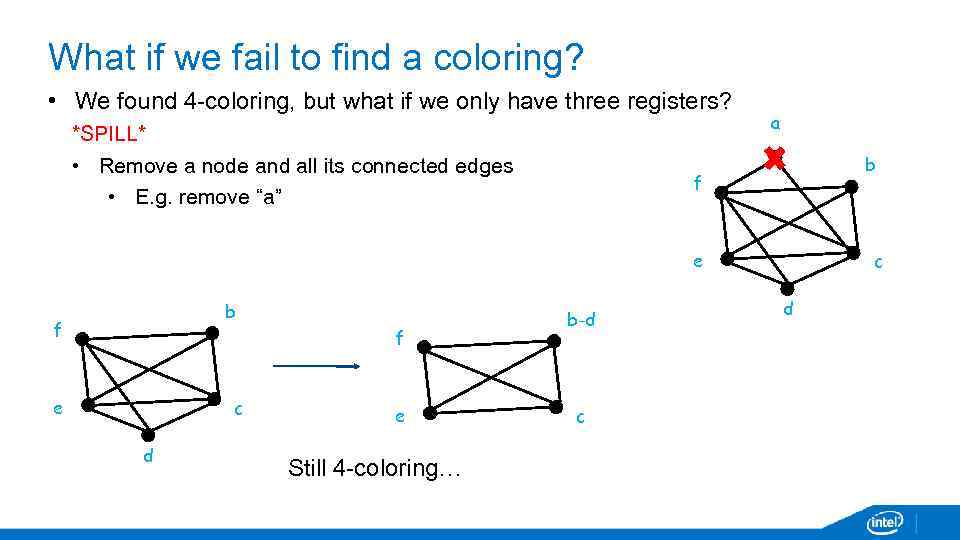What if we fail to find a coloring? • We found 4 -coloring, but what if we only have three registers? *SPILL* • Remove a node and all its connected edges • E. g. remove “a” a b f e b f f e c d e Still 4 -coloring… b-d c c d

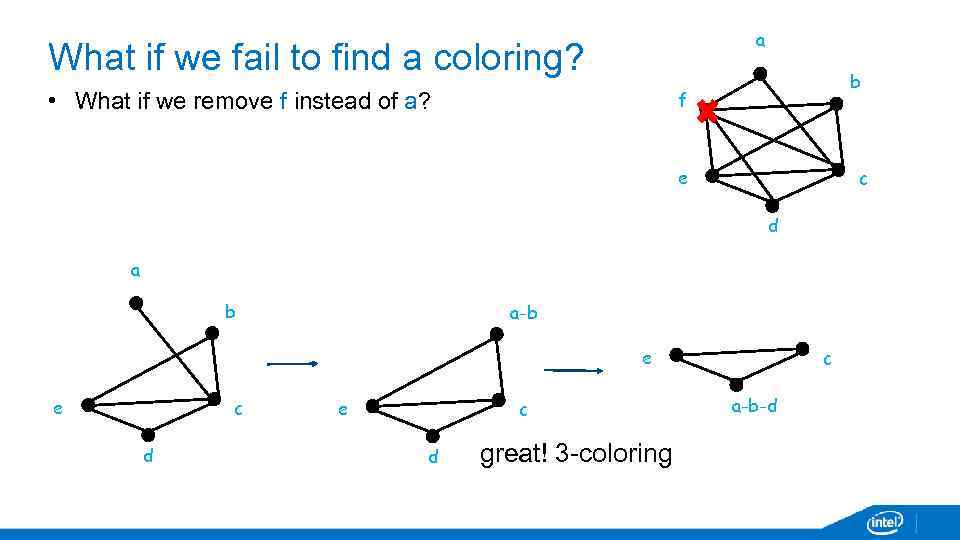a What if we fail to find a coloring? b f • What if we remove f instead of a? e c d a b a-b e e c d great! 3 -coloring c a-b-d

Spilling • What color do we assign to f? • After coloring reduced IG we can try to assign a color the deleted node • This is called “optimistic coloring” • If optimistic coloring failed, we need to spill f • Need to allocate a memory location for storing the value of it (usually it is stack) • Lets call the address of it fa • Before each operation that uses f, insert f : = load fa • After each operation that defines f, insert store f, fa

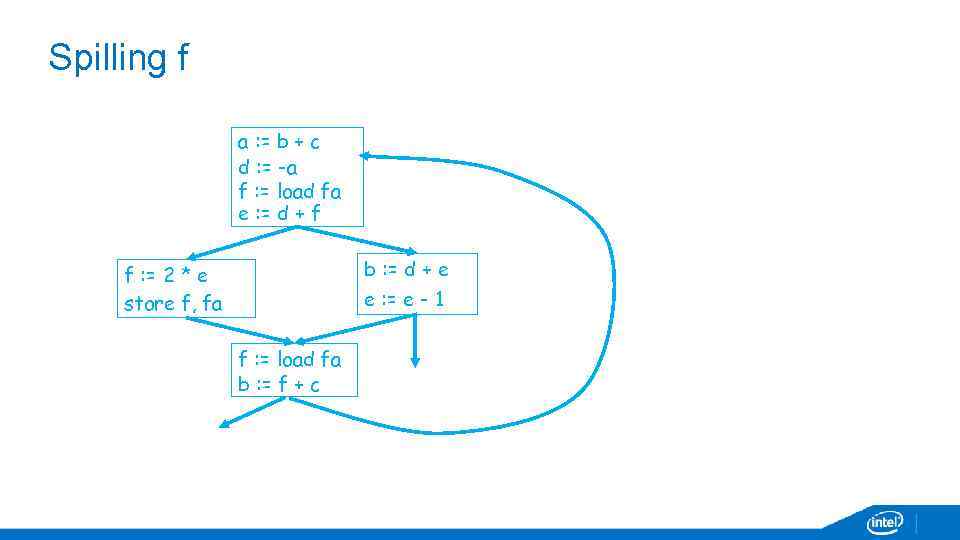Spilling f a : = b + c d : = -a f : = load fa e : = d + f b : = d + e f : = 2 * e store f, fa e : = e - 1 f : = load fa b : = f + c

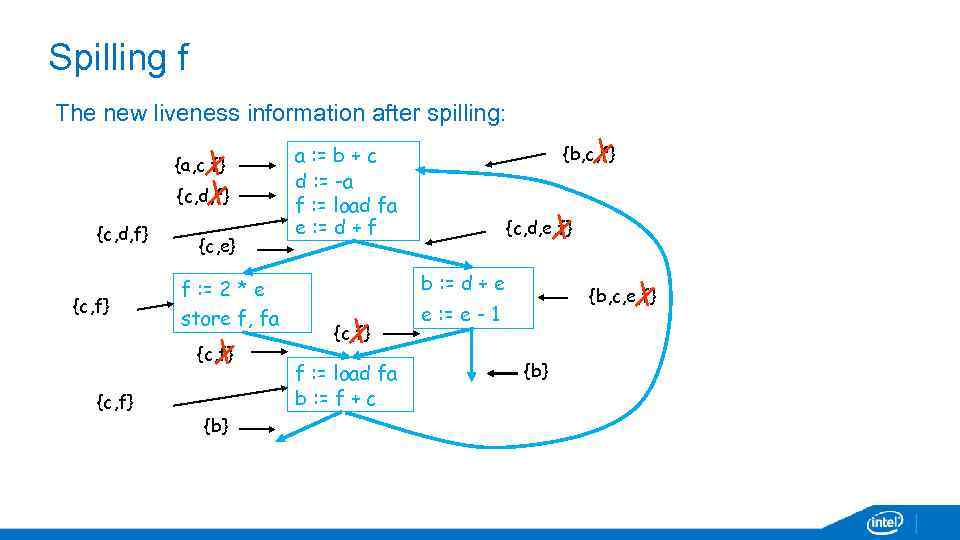Spilling f The new liveness information after spilling: {a, c, f} {c, d, f} {c, e} f : = 2 * e store f, fa {c, f} {b} a : = b + c d : = -a f : = load fa e : = d + f {b, c, f} {c, d, e, f} b : = d + e {c, f} f : = load fa b : = f + c {b, c, e, f} e : = e - 1 {b}

Spilling f • Spilling reduced the live range of the variable • And thus reduces its interference • Which resulted in fewer neighbors in IG

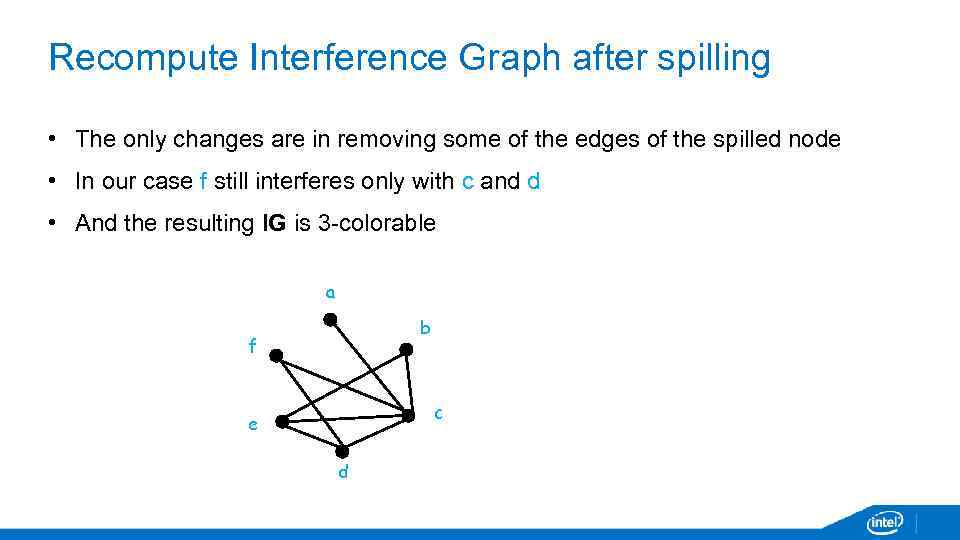Recompute Interference Graph after spilling • The only changes are in removing some of the edges of the spilled node • In our case f still interferes only with c and d • And the resulting IG is 3 -colorable a b f c e d

What to spill? Possible heuristics: § Spill variables with most conflicts § Spill variables with few definitions and uses § Avoid spilling in inner loops

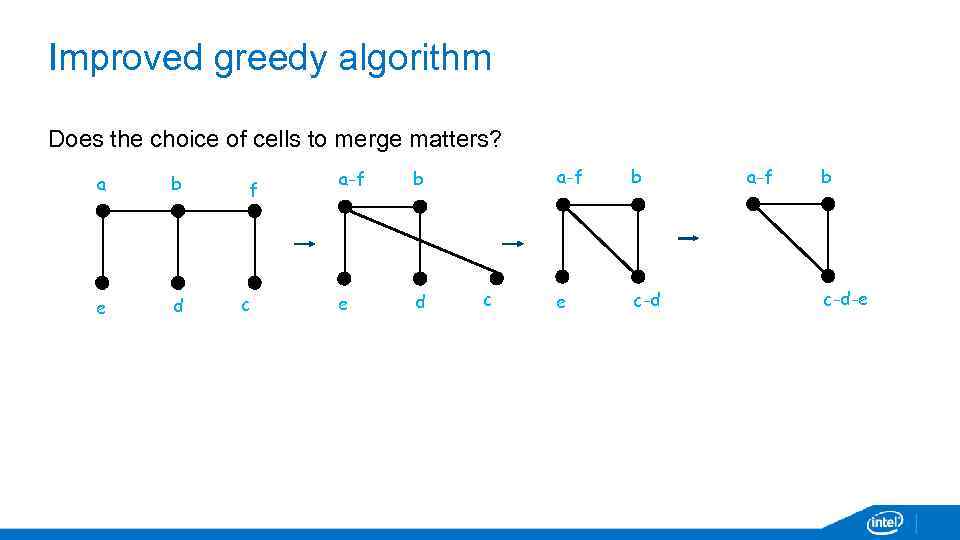Improved greedy algorithm Does the choice of cells to merge matters? a b e d f c a-f e d a-f b c b e c-d a-f b c-d-e

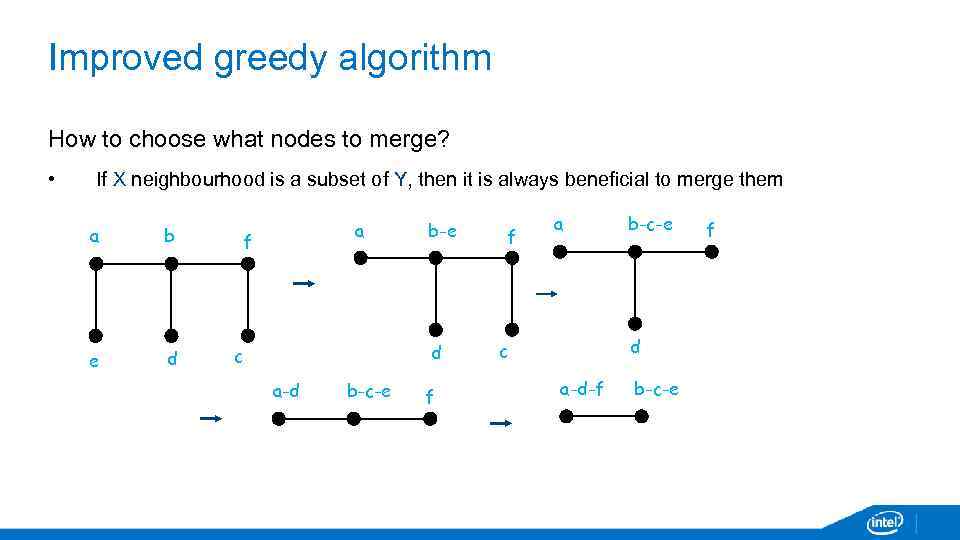Improved greedy algorithm How to choose what nodes to merge? • If X neighbourhood is a subset of Y, then it is always beneficial to merge them a b e d a f b-e d c a-d b-c-e f f a b-c-e d c a-d-f b-c-e f

Brute force algorithm? Any ideas?

Conclusion • Register allocation is a “must have” optimization in most compilers: § makes a big difference in performance • Graph coloring is a powerful register allocation scheme

Other areas in compiler where graphs matter • Intermediate representation • Finding loops • Know depth-first-search and how to find all strongly connected components! • Data flow analysis • Dominance frontier • Dead Code Elimination

Q&A alexander. ivchenko@intel. com

Thank You