Graph Algorithms Carl Tropper Department of Computer Science

Graph Algorithms Carl Tropper Department of Computer Science Mc. Gill University

Definitions • An undirected graph G is a pair (V, E), where V is a finite set of points called vertices and E is a finite set of edges. • An edge e ∈ E is an unordered pair (u, v), where u, v ∈ V. • In a directed graph, the edge e is an ordered pair (u, v). An edge (u, v) is incident from vertex u and is incident to vertex v. • A path from a vertex v to a vertex u is a sequence of vertices where v 0 = v, vk = u, and (vi, vi+1) ∈ E for I = 0, 1, …, k-1. • The length of a path is defined as the number of edges in the path.

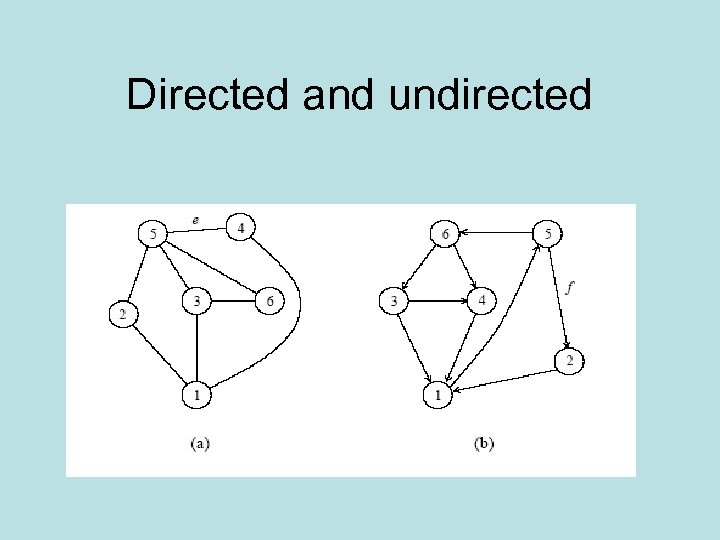Directed and undirected

More definitions • An undirected graph is connected if every pair of vertices is connected by a path. • A forest is an acyclic graph, and a tree is a connected acyclic graph. • A graph that has weights associated with each edge is called a weighted graph.

How to represent a graph 1 • Adjacency matrix represents undirected graph • (n 2)space to store matrix

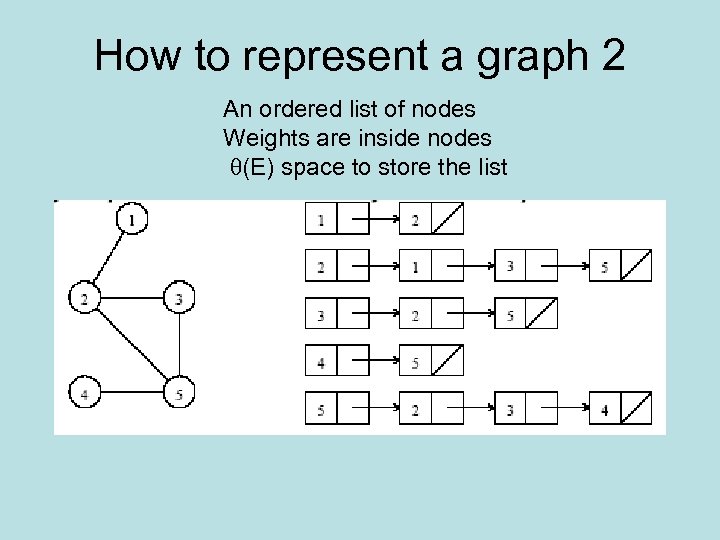How to represent a graph 2 An ordered list of nodes Weights are inside nodes (E) space to store the list

Which is better? • If graph is sparse, use pointers/list • If dense, then go with the adjacency matrix

MST: Prim’s Algorithm • A spanning tree of an undirected graph G is a subgraph of G which is (1) a tree and (2) contains all the vertices of G. • In a weighted graph, the weight of a subgraph is the sum of the weights of the edges in the subgraph. • A minimum spanning tree (MST) for a weighted undirected graph is a spanning tree with minimum weight.

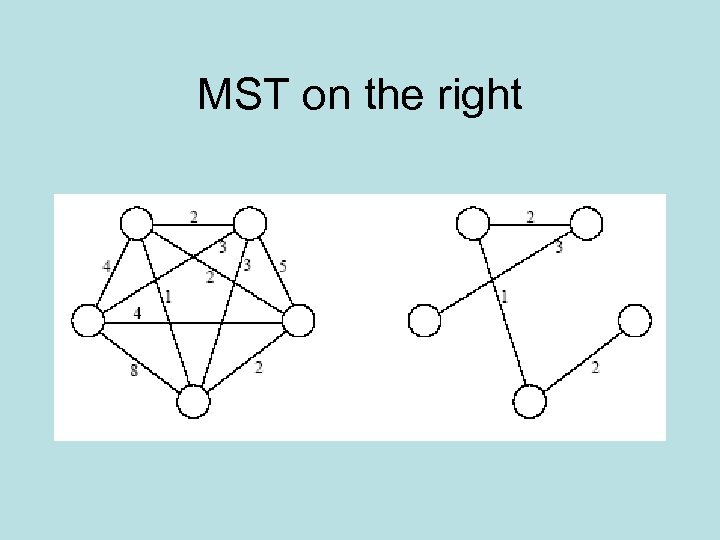MST on the right

Prim • is a greedy algorithm • Is recursive • Start by selecting an arbitrary vertex, include it into the current MST (the root) • Grow the current MST by inserting into it the vertex closest to one of the vertices already in current MST (the vertex which (1) is outside the MST and (2) adds the smallest weight to the MST)

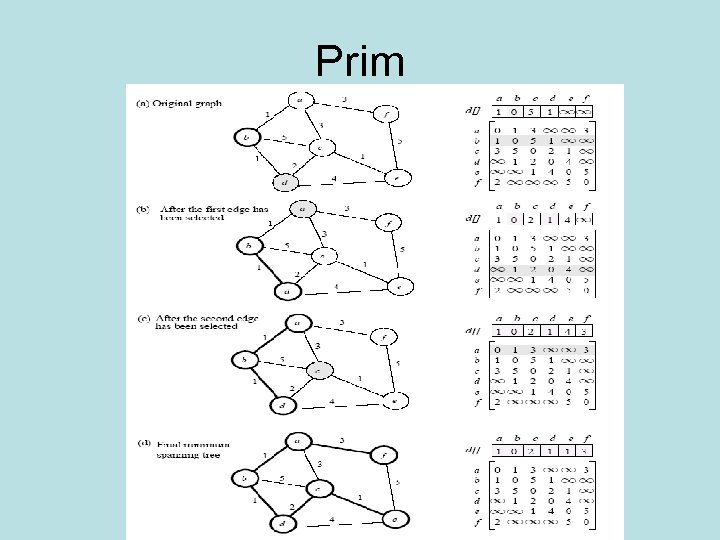Prim

Formal Prim Lines 10 -13 executed n-1 times 12 and 13 executed O(n) times Prim is (n 2)

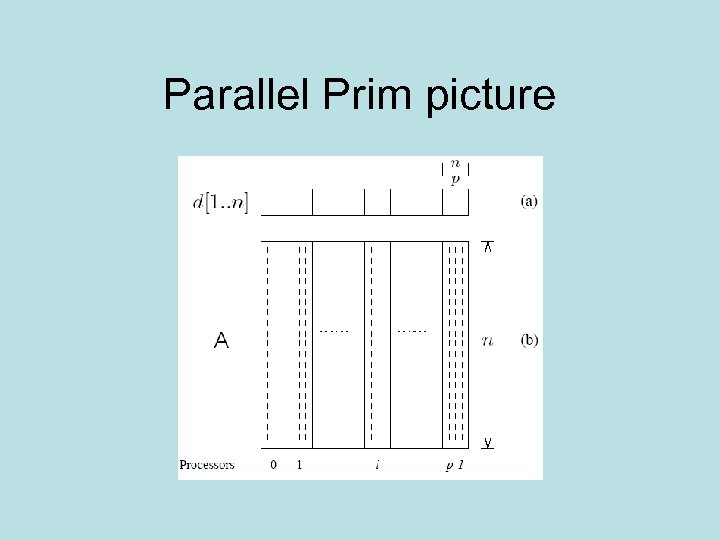
Parallel Prim • Let p be the number of processes, and let n be the number of vertices. • The adjacency matrix is partitioned in 1 -D block fashion, with distance vector d partitioned accordingly. • In each step, a processor selects the locally closest node, followed by a global (all to one) reduction to select globally closest node. One processor (say P 0) contains the MST. • This node is inserted into MST, and the choice broadcast (one to all) to all processors. • Each processor updates its part of the d vector locally.

Parallel Prim picture

Analysis • The cost to select the minimum entry is (n/p) • The cost of a broadcast is (log p). • The cost of local update of the d vector is (n/p). • The parallel time per iteration is (n/p + log p). • The total parallel time is given by (n 2/p + n log p). • The corresponding isoefficiency is (p 2 log 2 p).

Single source shortest path Dijkstra • For a weighted graph G = (V, E, w), the singlesource shortest paths problem is to find the shortest paths from a vertex v ∈ V to all other vertices in V. • Dijkstra's algorithm is similar to Prim's algorithm. It maintains a set of nodes for which the shortest paths are known. • It grows this set based on the node closest to source using one of the nodes in the current shortest path set. • The difference: Prim stores the cost of the minimal cost edge connecting a vertex in VT to u, Dijkstra stores minimal cost to reach u • Greedy algorithm

Single source analysis • The weighted adjacency matrix is partitioned using the 1 -D block mapping. • Each process selects, locally, the node closest to the source, followed by a global reduction to select next node. • The node is broadcast to all processors and the l-vector updated. • The difference: Prim stores the cost of the minimal cost edge connecting a vertex in VT to u, Dijkstra stores minimal cost to reach u • The parallel performance of Dijkstra's algorithm is identical to that of Prim's algorithm.

All Pairs Shortest Path • Given a weighted graph G(V, E, w), the all-pairs shortest paths problem is to find the shortest paths between all pairs of vertices vi, vj ∈ V. • Look at two versions of Dijkstra • And Floyd’s algorithm

First of all • Execute n instances of the singlesource shortest path problem, one for each of the n source vertices. • Complexity is (n 3) because complexity of shortest path algorithm is (n 2)

Two strategies • Source partitioned-execute n shortest path problems on n processors. Each of the n nodes gets to be a source node. • Source parallel-partition adjacency matrix a la Prim

Dijkstra: Source Partitioned • Use n processors, each processor Pi finds the shortest paths from vertex vi to all other vertices by executing Dijkstra's sequential single-source shortest paths algorithm. • It requires no interprocess communication (provided that the adjacency matrix is replicated at all processes). • The parallel run time of this formulation is: Θ(n 2). • While the algorithm is cost optimal, it can only use n processors. Therefore, the isoefficiency due to concurrency is p 3.

Dijkstra: Source Parallel • Want to keep more then n processors busy • Given p processors (p > n), each single source shortest path problem is executed by one on one of n partitions • Use p/n processors for each of the problems • From before, the parallel time is: TP= Θ(n 3/p) {computation}+ Θ(n log p) {communication} • For cost optimality, we have p = O(n 2/log n) and the isoefficiency is Θ((p log p)1. 5).

Floyd’s • For any pair of vertices vi, vj ∈ V, consider all paths from vi to vj whose intermediate vertices belong to the set {v 1, v 2, …, vk}. Let pi(, kj) (of weight di(, kj) be the minimum-weight path among them. • If vertex vk is not in the shortest path from vi to vj, then pi(, kj) is the same as pi(, kj-1). • If f vk is in pi(, kj), then we can break pi(, kj) into two paths - one from vi to vk and one from vk to vj. Each of these paths uses vertices from {v 1, v 2, …, vk-1}.

Recurrence From our observations, the following recurrence relation follows: This equation must be computed for each pair of nodes and for k = 1, n. The serial complexity is O(n 3).

Floyd This program computes the all-pairs shortest paths of the graph G = (V, E) with adjacency matrix A.

Parallel Floyd • Matrix D(k) is divided into p blocks of size (n / √p) x (n / √p) {n 2/p elements per block} • Each processor updates its part of the matrix during each iteration. • To compute dl(, kk-1) processor Pi, j must get dl(, kk -1) and d ( k -1). k, r • In general, during the kth iteration, each of the √p processes containing part of the kth row send it to the √p - 1 processes in the same column. • Similarly, each of the √p processes containing part of the kth column sends it to the √p - 1 processes in the same row.

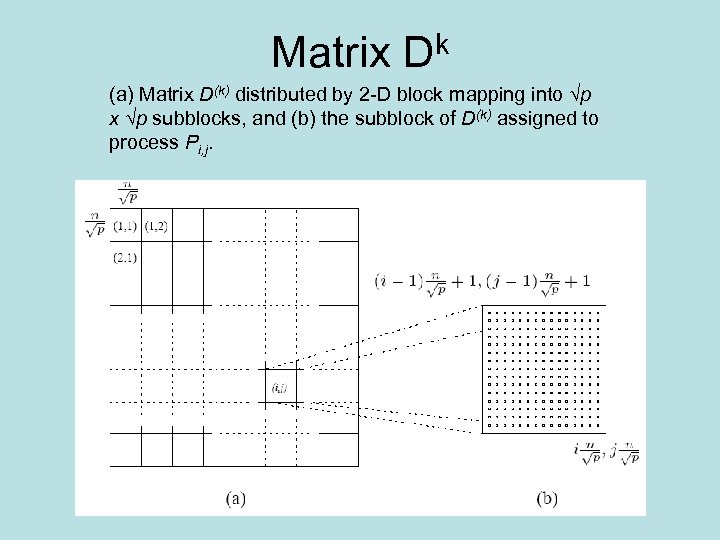Matrix Dk (a) Matrix D(k) distributed by 2 -D block mapping into √p x √p subblocks, and (b) the subblock of D(k) assigned to process Pi, j.

Communication • In general, during the kth iteration, each of the √p processes containing part of the kth row send it to the √p - 1 processes in the same column. • Similarly, each of the √p processes containing part of the kth column sends it to the √p - 1 processes in the same row.

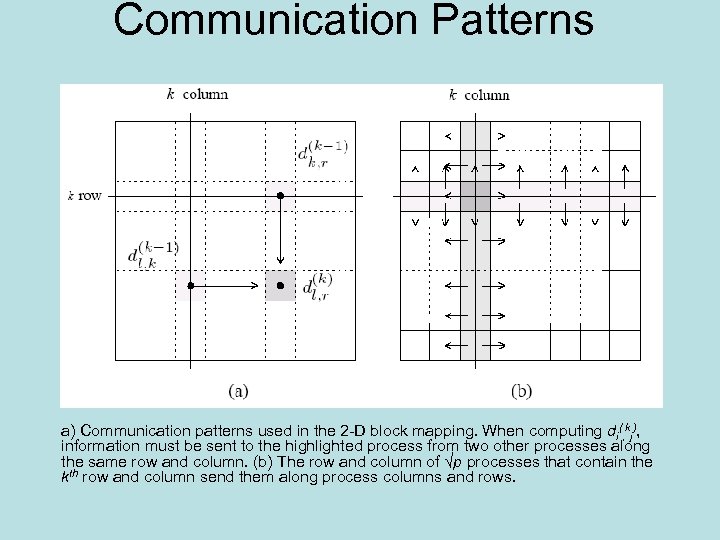Communication Patterns a) Communication patterns used in the 2 -D block mapping. When computing di(, kj), information must be sent to the highlighted process from two other processes along the same row and column. (b) The row and column of √p processes that contain the kth row and column send them along process columns and rows.

Floyd-Parallel Formulation Floyd's parallel formulation using the 2 -D block mapping. P*, j denotes all the processes in the jth column, and Pi, * denotes all the processes in the ith row. The matrix D(0) is the adjacency matrix.

Analysis • During each iteration of the algorithm, the kth row and kth column of processors perform a one-to-all broadcast along their rows/columns. • The size of this broadcast is n/√p elements, taking time Θ((n log p)/ √p). • The synchronization step takes time Θ(log p). • The computation time is Θ(n 2/p) • There are n iterations of the algorithm {k=1, . . , n} • The parallel run time of the 2 -D block mapping formulation of Floyd's algorithm is

Analysis II • The above formulation can use O(n 2 / log 2 n) processors cost-optimally. • The isoefficiency of this formulation is Θ(p 1. 5 log 3 p). • This algorithm can be further improved by relaxing the strict synchronization after each iteration • Go to next slide

Pipelining Floyd • The synchronization step in parallel Floyd's algorithm can be removed without affecting the correctness of the algorithm. • A process starts working on the kth iteration as soon as it has computed the (k-1)th iteration and has the relevant parts of the D(k-1) matrix.

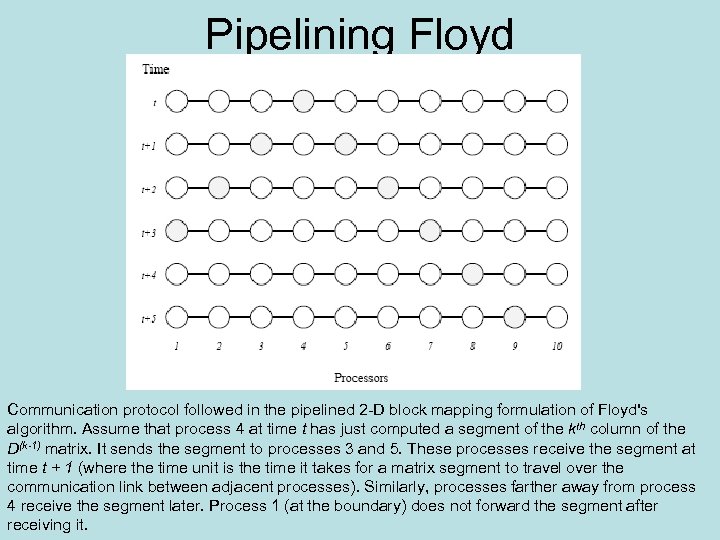Pipelining Floyd Communication protocol followed in the pipelined 2 -D block mapping formulation of Floyd's algorithm. Assume that process 4 at time t has just computed a segment of the kth column of the D(k-1) matrix. It sends the segment to processes 3 and 5. These processes receive the segment at time t + 1 (where the time unit is the time it takes for a matrix segment to travel over the communication link between adjacent processes). Similarly, processes farther away from process 4 receive the segment later. Process 1 (at the boundary) does not forward the segment after receiving it.

Pipelining Analysis • In each step, n/√p elements of the first row are sent from process Pi, j to Pi+1, j. • Similarly, elements of the first column are sent from process Pi, j to process Pi, j+1. • Each such step takes time Θ(n/√p). • After Θ(√p) steps, process P√p , √p gets the relevant elements of the first row and first column in time Θ(n). • The values of successive rows and columns follow after time Θ(n 2/p) in a pipelined mode. • Process P√p , √p finishes its share of the shortest path computation in time Θ(n 3/p) + Θ(n). • When process P√p , √p has finished the (n-1)th iteration, it sends the relevant values of the nth row and column to the other processes.

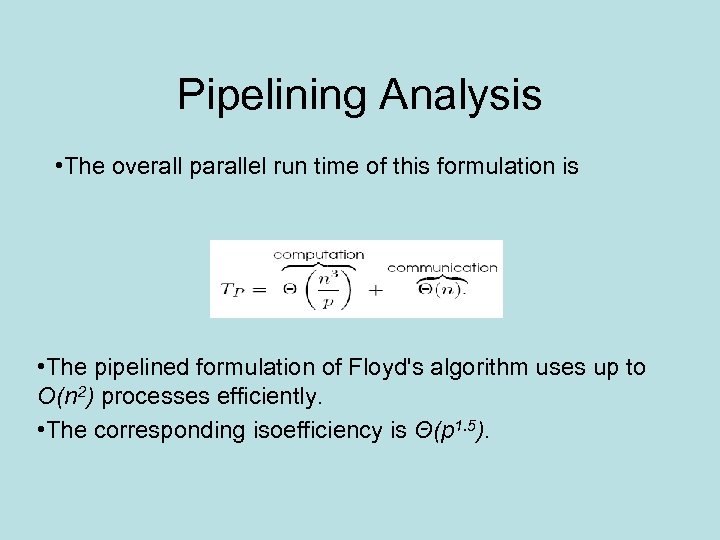Pipelining Analysis • The overall parallel run time of this formulation is • The pipelined formulation of Floyd's algorithm uses up to O(n 2) processes efficiently. • The corresponding isoefficiency is Θ(p 1. 5).

Comparison of shortest path algorithms Assumption: Parallel architecture has O(p) bisection bandwith {minimum communication between 2 halves of network} Conclusion: Pipelined Floyd is the most scalable-lowest iso and run time and can use (n 2) processors

Transitive Closure of a Graph • If G = (V, E) is a graph, then the transitive closure of G is defined as the graph G* = (V, E*), where E* = {(vi, vj) | there is a path from vi to vj in G} • The connectivity matrix of G is a matrix A* = (ai*, j) such that ai*, j = 1 if there is a path from vi to vj or i = j, and ai*, j = ∞ otherwise. • To compute A* we assign a weight of 1 to each edge of E and use an all-pairs shortest paths algorithm on the graph.

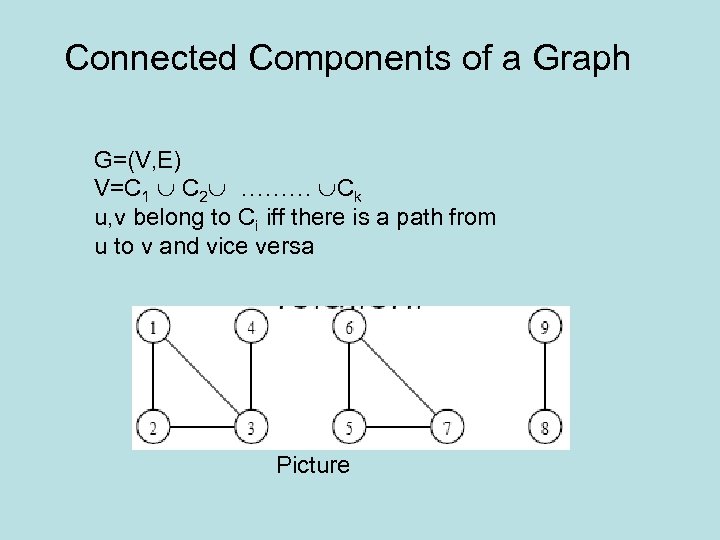Connected Components of a Graph G=(V, E) V=C 1 C 2 ……… Ck u, v belong to Ci iff there is a path from u to v and vice versa Picture

Depth First Search • Perform DFS on the graph to get a forest each tree in the forest corresponds to a connected component. • b has the components • Each component is a tree

Parallel Component algorithm • Partition adjacency matrix into p subgraphs Gi and assign each Gi to a process Pi • Each Pi computes spanning forest of Gi • Merge spanning forests pair wise until there is one spanning forest

Parallel Components

Ops for merging • Algorithm uses disjoint sets of edges. • Ops for the disjoint sets: • find(x) – returns a pointer to the representative element of the set containing x. Each set has its own unique representative. • union(x, y) – unites the sets containing the elements x and y.

Merging Ops • For merging forest A into forest B, for each edge (u, v) of A, a find operation is performed to determine if the vertices are in the same tree of B. • If not, then the two trees (sets) of B containing u and v are united by a union operation. • Otherwise, no union operation is necessary. • Merging A and B requires at most 2(n-1) find operations and (n-1) union operations.

Parallel Block Mapping • The n x n adjacency matrix is partitioned into p blocks. • Each processor can compute its local spanning forest in time Θ(n 2/p). • Merging is done by embedding a logical tree into the topology. There are log p merging stages, and each takes time Θ(n). Thus, the cost due to merging is Θ(n log p). • During each merging stage, spanning forests are sent between nearest neighbors. Θ(n) edges of the spanning forest are transmitted

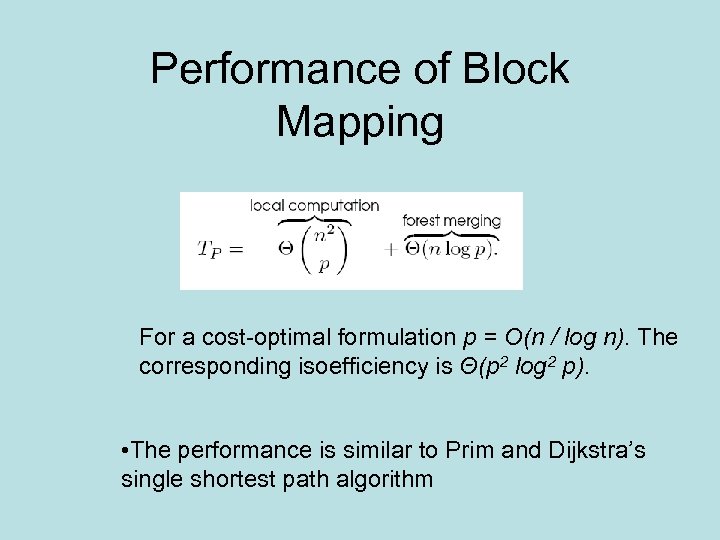Performance of Block Mapping For a cost-optimal formulation p = O(n / log n). The corresponding isoefficiency is Θ(p 2 log 2 p). • The performance is similar to Prim and Dijkstra’s single shortest path algorithm

Sparse Graphs • A graph G = (V, E) is sparse if |E| is much smaller than |V|2

Algorithms for sparse graphs • Can reduce the complexity of dense graph algorithms by making use of adjacency list instead of adjacency graph – E. g. Prim’s algorithm is Θ(n 2) for a dense matrix and Θ(|E| log n) for a sparse matrix • Key to good performance of dense matrix algorithms was the ability to assign roughly equal workloads to all of the processors and to keep the communication local • Floyd-assigned equal size blocks from the adjacency matrix of consecutive rows and columns=>local communication

Sparse difficulties • Partitioning adjacency matrix is harder then it looks • Assign equal # vertices to processors + their adjacency lists. Some processors may have more links then others. • Assign equal # links=> need to split adjacency list of a vertex among processors=>lots of communication • Works for “certain” structures-next slide

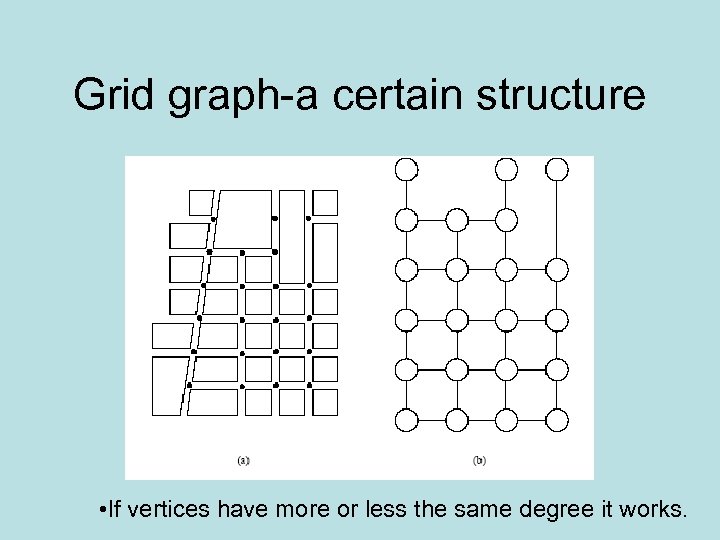Grid graph-a certain structure • If vertices have more or less the same degree it works.

Maximal Independent Set • A set of vertices I ⊂ V is called independent if no pair of vertices in I is connected via an edge in G. An independent set is called maximal if by including any other vertex not in I, the independence property is violated.

Who cares? • Maximal independent sets can be used to find how many parallel tasks from a task graph can be executed • Used in graph coloring algorithms

Simple MIS algorithm • start with empty MIS I, and assign all vertices to a candidate set C. • Vertex v from C is moved into I and all vertices adjacent to v are removed from C. • This process is repeated until C is empty. • Problem: serial algorithm

Luby’s algorithm • In the beginning C is set equal to V, I is empty • Assign random numbers to all of the nodes of the graph • If vertex has a smaller random # the all of its adjacent vertices, then • put it in I • Delete all of its adjacent neighbors from C • Repeat above steps until C is empty • Takes O(log |V|) steps on the average • Luby invented this algorithm for graph coloring

Parallel Luby for Shared Address Space • 3 arrays of size |V| • I: idependence array I(i)=1 if i is in MIS. Initially all I(i)=0 • R: random number array • C: candidate array C(i)=1 if i is a candidate • Partition C among p processes • Each process generates random number for each of its vertices • Each process checks to see if random numbers of its vertices are smaller then those of adjacent vertices • Process zeroes entries corresponding to adjacent entries

Single Source Shortest Paths • 2 steps happen in each iteration • Extract u (V-VT) such that l[u]=min[l[v]], v V-VT • For each vertex in (V-VT), compute l[v]=min[l[v], l[u] + w(u, v)] • Make sense to use adjacency list for last equation • Use priority queue to store l values with smallest on top • Priority queue implemented with binary heap

Johnson Updating vertices in the heap is the big time sink-O(log n) per update and |E| updates=> (|E|log n) complexity

Parallel Johnson-first attempts • Use one processor P 0 to house the queueother processes update l[v] and give them to P 0 • Problems: • Single queue is a bottleneck • Small number of processes can be kept busy (|E|/|V|) • So distribute queue to processes. • Need low latency architecture to make this work

First atttempts-continued • Still have low speedup (O(log n)) if each update takes O(1)) • Can extract multiple nodes from queueall vertices u with same minimum distance • Why? Can process nodes with same distance in any order • Still not enough speedup

Solution-speculative decomposition • When process Pi extracts the vertex u ∈ Vi, it sends a message to processes that store vertices adjacent to u. • Process Pj, upon receiving this message, sets the value of l[v] stored in its priority queue to min{l[v], l[u] + w(u, v)}. • If a shorter path has been discovered to node v, it is reinserted back into the local priority queue. • The algorithm terminates only when all the queues become empty.

Speculative decomposition Distributed Memory • Partition queue among the processors • Partition vertices and adjacency lists among the processors • Each processor updates its local queue and sends the results to the processors with adjacent vertices • Recipient processor updates its value for shortest path

More precisely • For example: u Pi and v Pj and (u. v) is an edge. Pi extracts u and updates l[u] • Pi sends message to Pj with new value for v, which is l[u]+w(u, v). • Pj compares l[u]+w(u, v) to sp[v] • If smaller, then have new sp[v] • If larger, then discard

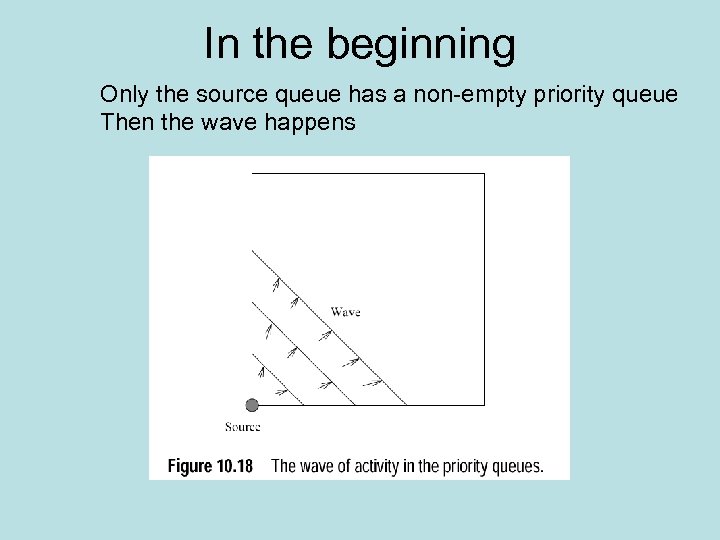In the beginning Only the source queue has a non-empty priority queue Then the wave happens

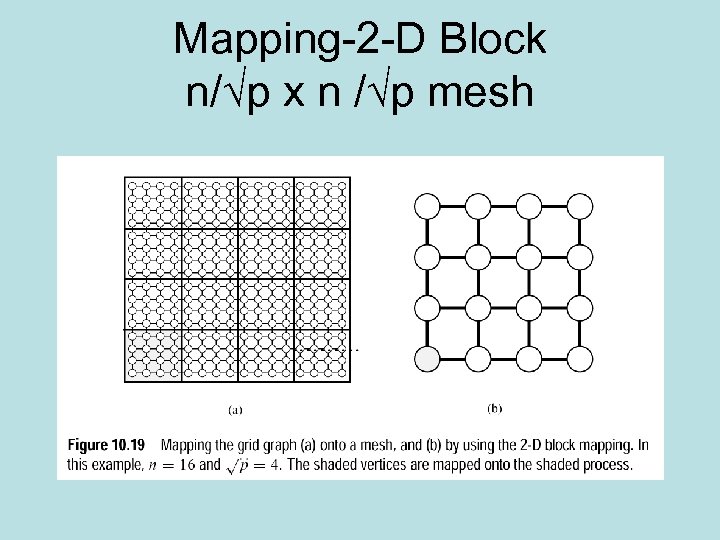Mapping-2 -D Block n/√p x n /√p mesh

Analysis of 2 -D • At most O( p) processes are busy at any time because the wave moves diagonally (diagonal= p) • Max speedup is S=W/W/√p= √p • E=1/√p • Lousy efficiency

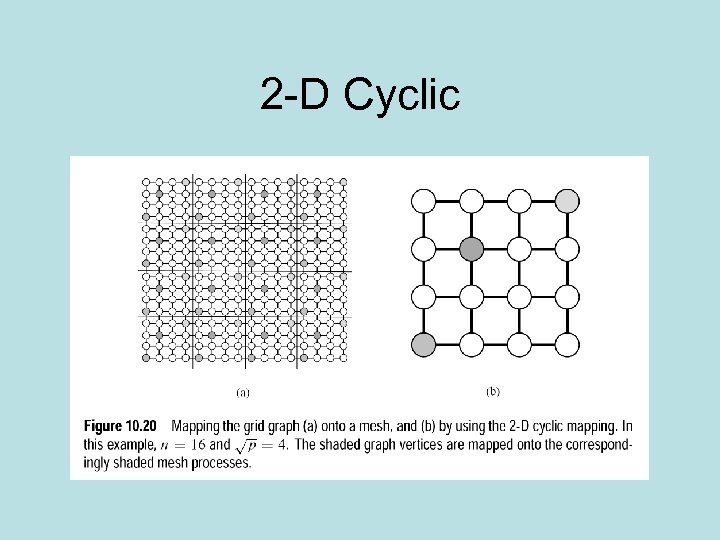2 -D Cyclic

Analysis • Improves things because vertices are further apart • Bad news: more communication

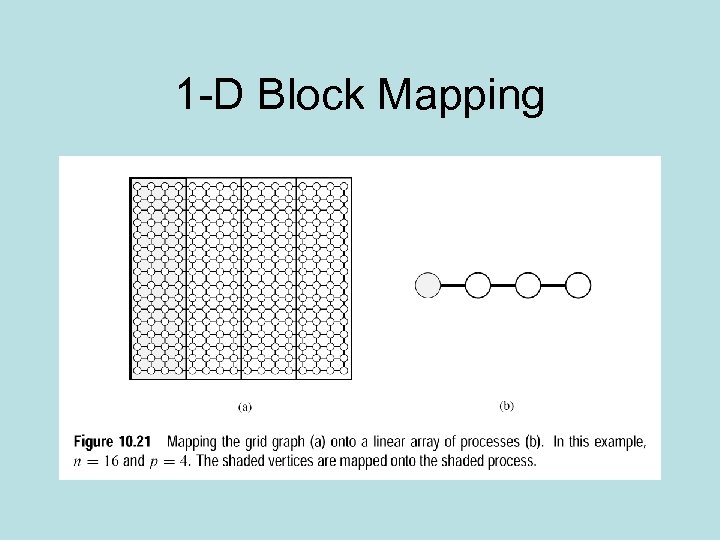1 -D Block Mapping

1 -D rules • Better idea because as wave spreads more processors get involved concurrently • Assume p/2 processes are busy, then • S=W/W/p/2=p/2 • E=1/2 • Improvement over 2 -D • Bad side-uses O(n) processes