Графики функций с модулями Выполнил ученик 10 -Ф

Графики функций с модулями Выполнил ученик 10 -Ф класса Зуевский Олег

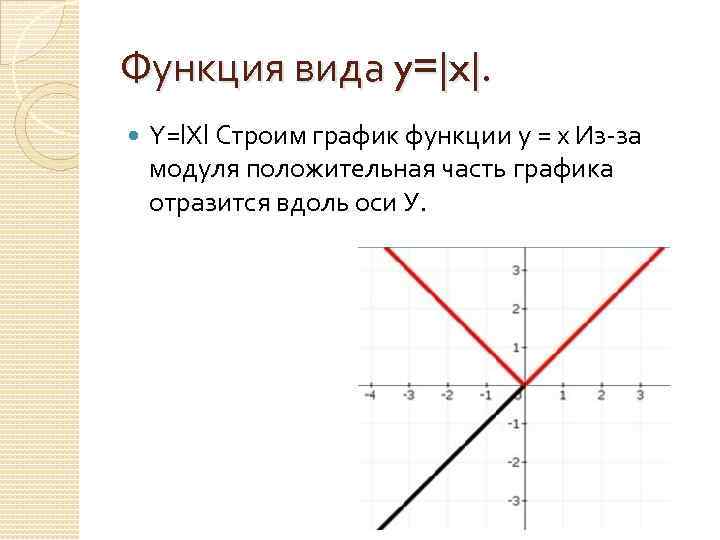Функция вида y=|x|. Y=l. Xl Строим график функции у = x Из-за модуля положительная часть графика отразится вдоль оси У.

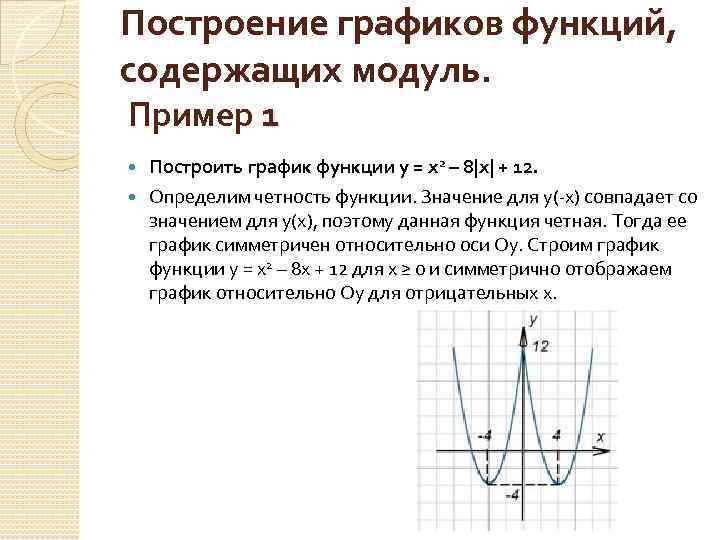Построение графиков функций, содержащих модуль. Пример 1 Построить график функции y = x 2 – 8|x| + 12. Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x 2 – 8 x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x.

Пример 2 Следующий график вида y = |x 2 – 8 x + 12|. Это значит, что график функции получают следующим образом: строят график функции y = x 2– 8 x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox

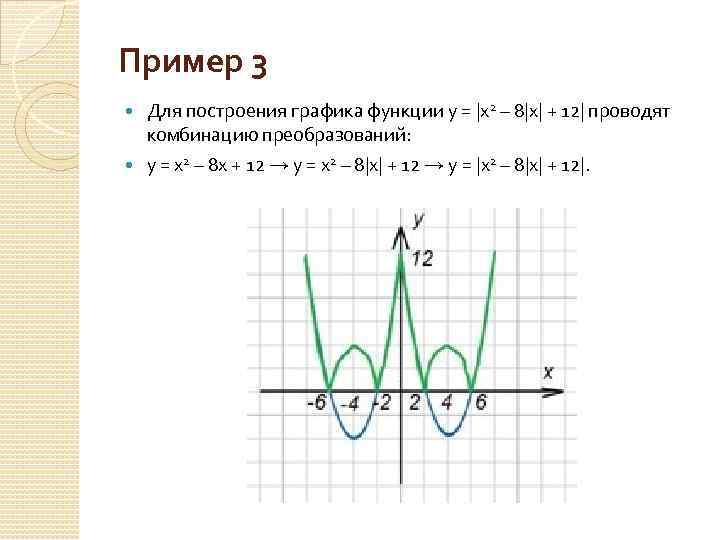Пример 3 Для построения графика функции y = |x 2 – 8|x| + 12| проводят комбинацию преобразований: y = x 2 – 8 x + 12 → y = x 2 – 8|x| + 12 → y = |x 2 – 8|x| + 12|.

Рассмотренные преобразования справедливы для всех видов функций. Составим таблицу:

У=l 10 х+4 l Строим график функции у=10 х+4 Подставляем модуль и функция станет положительной во всей области определения. Положительная часть первой функции отразится от х=-0, 4

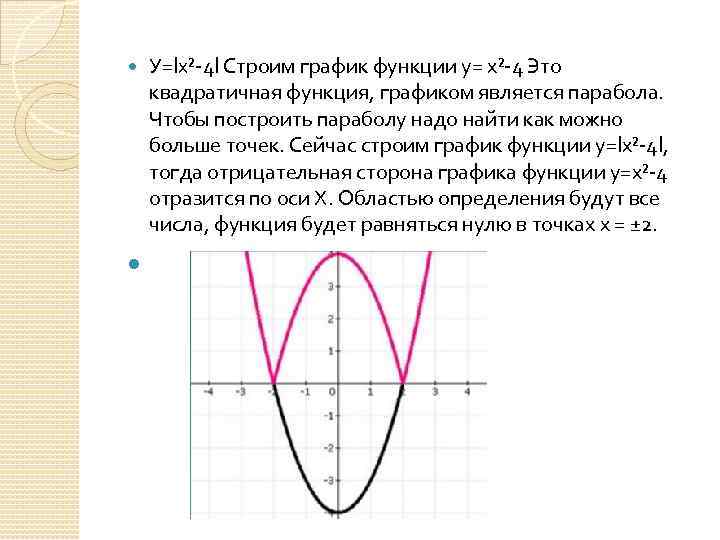У=lx²-4 l Строим график функции у= х²-4 Это квадратичная функция, графиком является парабола. Чтобы построить параболу надо найти как можно больше точек. Сейчас строим график функции у=lх²-4 l, тогда отрицательная сторона графика функции у=х²-4 отразится по оси Х. Областью определения будут все числа, функция будет равняться нулю в точках х = ± 2.

У=2 х²-5 lхl-7 Строим график функции у=2 х²-5 х -7, приравняем нулю и получим два корня х=3, 5 и х’=-1 Найдём вершину функции. В точке х=1, 5 у=-10 Строим график функции у=2 х²-5 lхl-7.

У=l 2 х²-5 lхl-7 l – сложная функция. Строим сперва график функции у=2 х²-5 lхl-7 как в 4 -ом слайде. Потом всю эту функцию берём под модуль. Функция у=l 2 х²-5 lхl-7 l будет положительным на всей области определения. Функция будет равняться нулю в точках х=± 3, 5 У=l 2 х²-5 lхl-7 l – сложная функция. Строим сперва график функции у=2 х²-5 lхl-7 как в 4 ом слайде. Потом всю эту функцию берём под модуль. Функция у=l 2 х²-5 lхl-7 l будет положительным на всей области определения. Функция будет равняться нулю в точках х=± 3, 5

У=lх²+хl Строим гр. ф у=х²+х Эта квадратичная функция, графиком является парабола. Чтобы построить параболу надо как можно больше точек. Строим гр. ф у=lх²+хl Отрицательная сторона отразится в положительную сторону по оси Х. X 1 -1 0 -2 Y 2 0 0 2

ц е н о К