График производной функции На рисунке


![Пример В какой точке отрезка [– 4; – 1] функции у =f Пример В какой точке отрезка [– 4; – 1] функции у =f](https://present5.com/presentation/3/15595804_155010924.pdf-img/15595804_155010924.pdf-9.jpg)
![Пример В какой точке отрезка [– 4; – 1] функции у =f Пример В какой точке отрезка [– 4; – 1] функции у =f](https://present5.com/presentation/3/15595804_155010924.pdf-img/15595804_155010924.pdf-10.jpg)
![Пример В какой точке отрезка [ 0; 3] функции у =f (x) Пример В какой точке отрезка [ 0; 3] функции у =f (x)](https://present5.com/presentation/3/15595804_155010924.pdf-img/15595804_155010924.pdf-11.jpg)
![Пример В какой точке отрезка [ 1; 4] функции у =f (x) Пример В какой точке отрезка [ 1; 4] функции у =f (x)](https://present5.com/presentation/3/15595804_155010924.pdf-img/15595804_155010924.pdf-12.jpg)
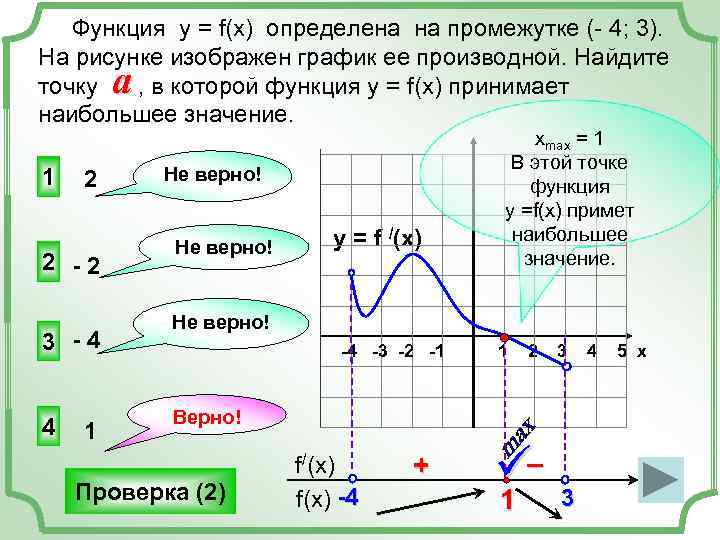
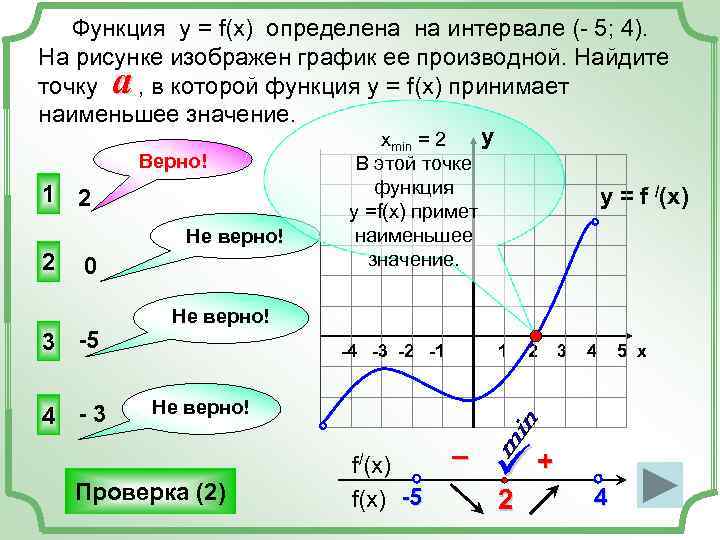
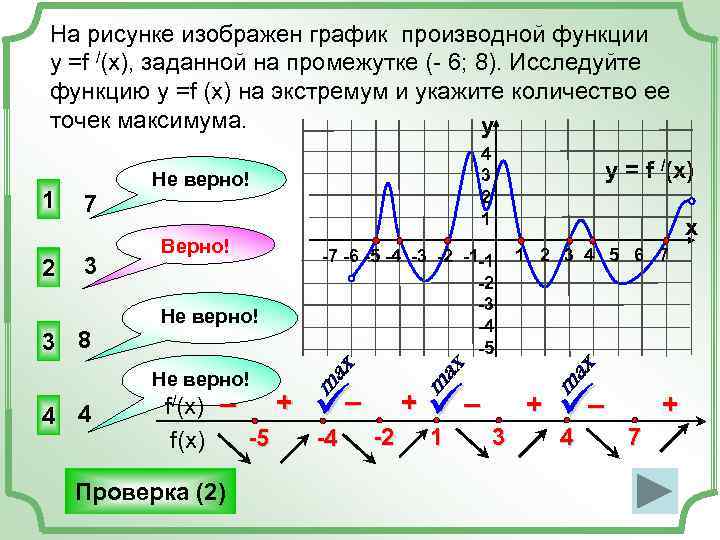
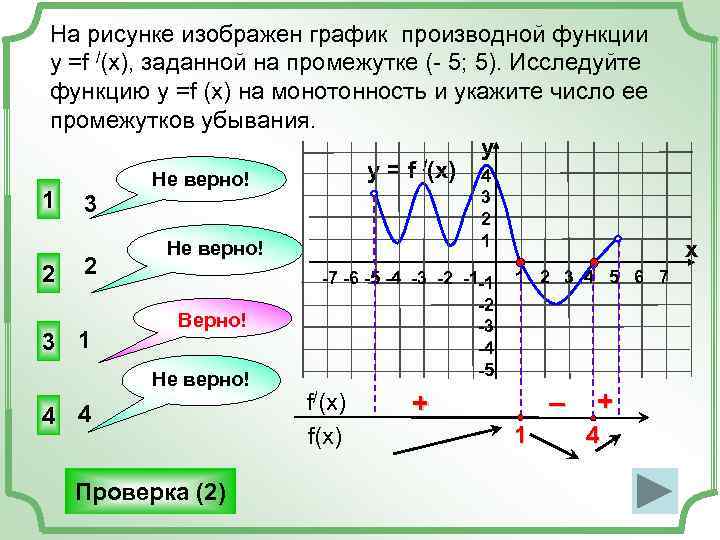
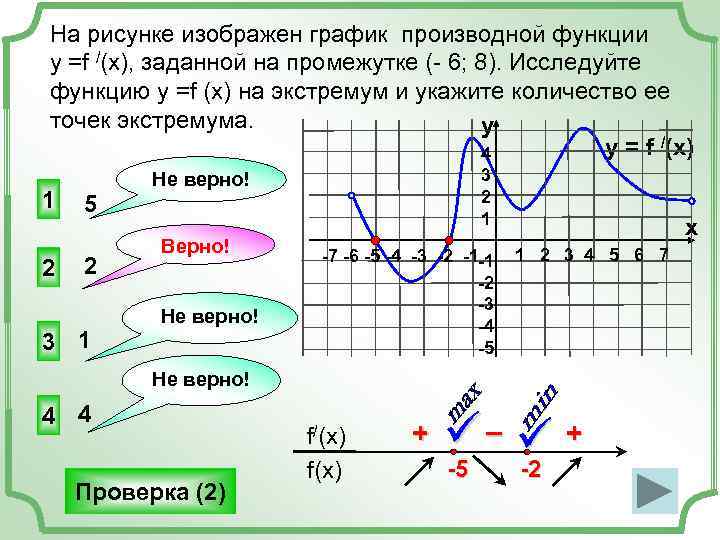
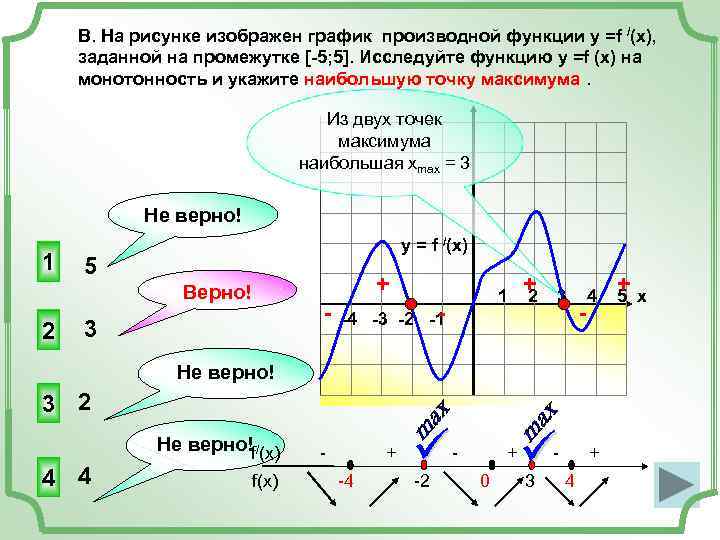
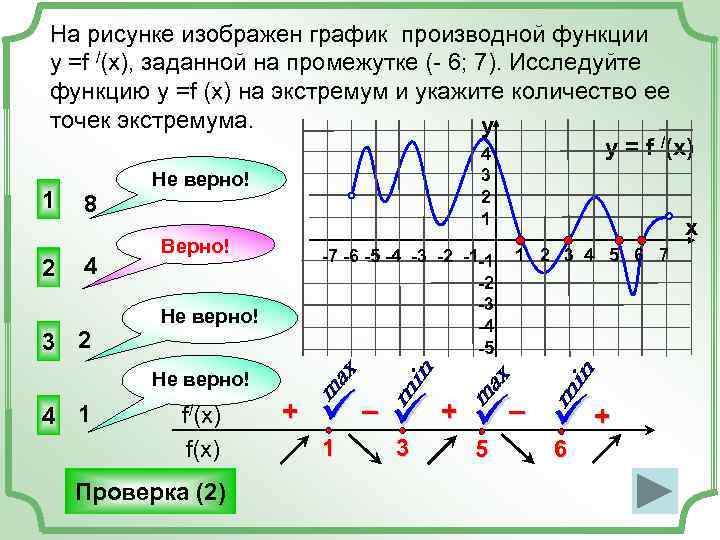
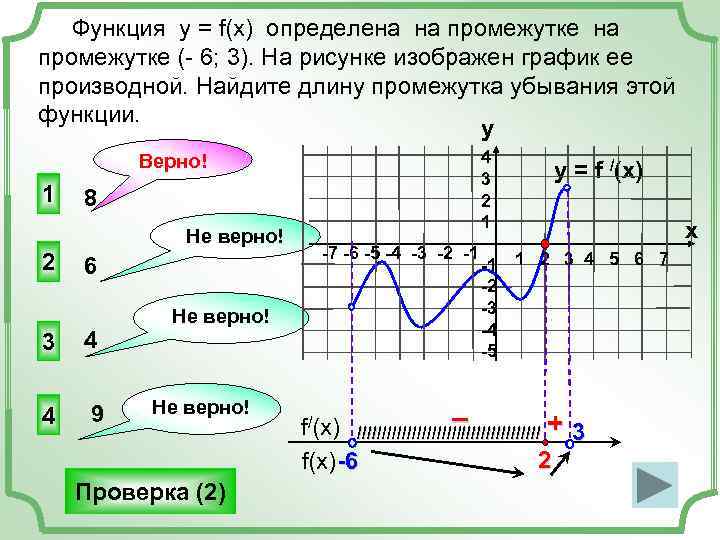
график производной функции.ppt
- Количество слайдов: 20
 График производной функции
График производной функции
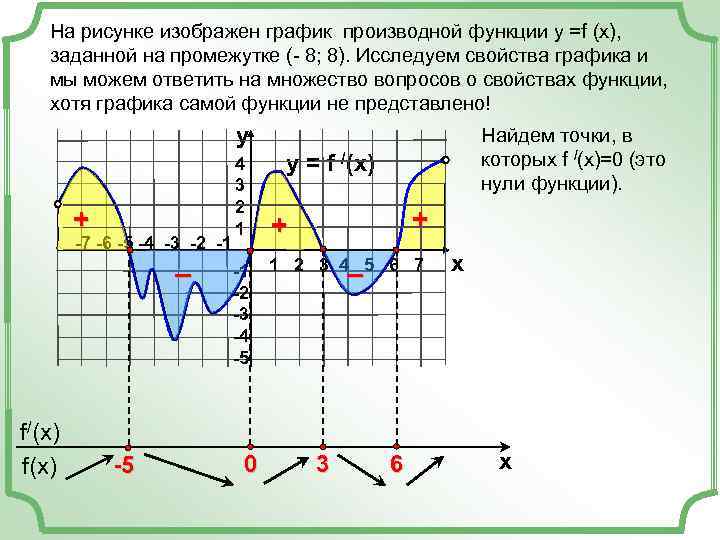
 На рисунке изображен график производной функции у =f (x), заданной на промежутке (- 8; 8). Исследуем свойства графика и мы можем ответить на множество вопросов о свойствах функции, хотя графика самой функции не представлено! y Найдем точки, в 4 y = f /(x) которых f /(x)=0 (это 3 нули функции). 2 + 1 + -7 -6 -5 -4 -3 -2 -1 – -1 1 2 3 4 5 6 7 – x -2 -3 -4 -5 f/(x) f(x) -5 0 3 6 x
На рисунке изображен график производной функции у =f (x), заданной на промежутке (- 8; 8). Исследуем свойства графика и мы можем ответить на множество вопросов о свойствах функции, хотя графика самой функции не представлено! y Найдем точки, в 4 y = f /(x) которых f /(x)=0 (это 3 нули функции). 2 + 1 + -7 -6 -5 -4 -3 -2 -1 – -1 1 2 3 4 5 6 7 – x -2 -3 -4 -5 f/(x) f(x) -5 0 3 6 x
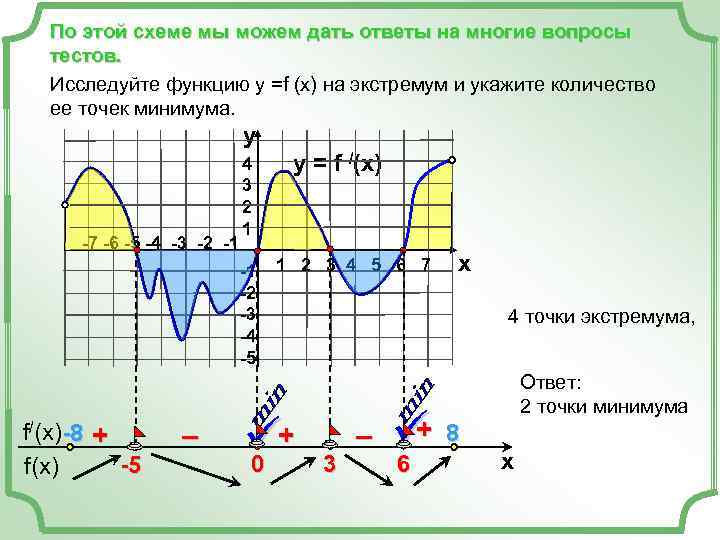
 По этой схеме мы можем дать ответы на многие вопросы тестов. Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума. y 4 y = f /(x) 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 4 точки экстремума, -4 -5 Ответ: 2 точки минимума f/(x)-8 + – ü + – ü 8 6 + x f(x) -5 0 3
По этой схеме мы можем дать ответы на многие вопросы тестов. Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума. y 4 y = f /(x) 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 4 точки экстремума, -4 -5 Ответ: 2 точки минимума f/(x)-8 + – ü + – ü 8 6 + x f(x) -5 0 3
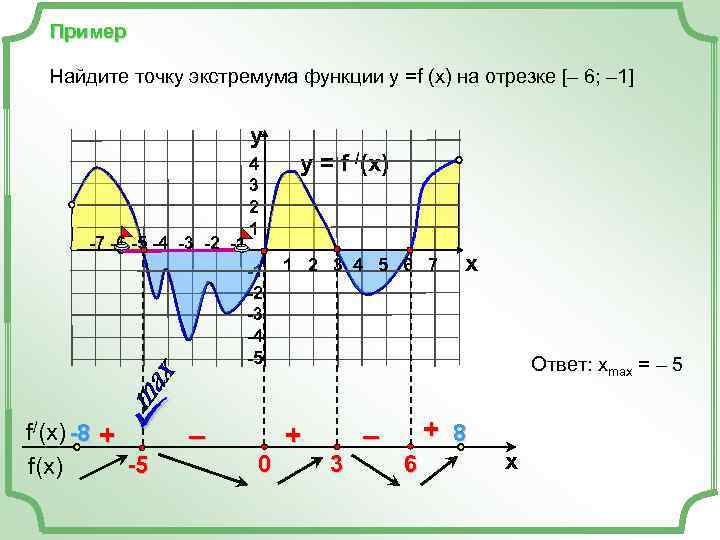
 Пример Найдите точку экстремума функции у =f (x) на отрезке [– 6; – 1] y 4 y = f /(x) 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 -4 -5 Ответ: xmax = – 5 f/(x) -8 + ü – + – + 8 f(x) -5 0 3 6 x
Пример Найдите точку экстремума функции у =f (x) на отрезке [– 6; – 1] y 4 y = f /(x) 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 -4 -5 Ответ: xmax = – 5 f/(x) -8 + ü – + – + 8 f(x) -5 0 3 6 x
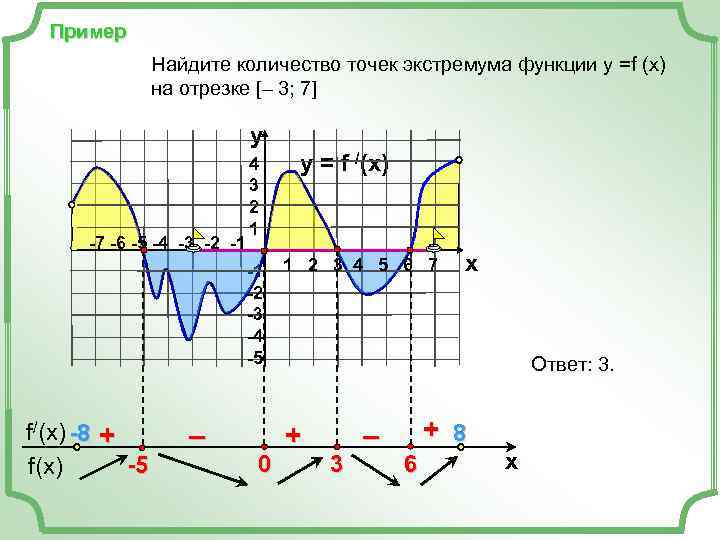
 Пример Найдите количество точек экстремума функции у =f (x) на отрезке [– 3; 7] y 4 y = f /(x) 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 -4 -5 Ответ: 3. f/(x) -8 + – + – + 8 f(x) -5 0 3 6 x
Пример Найдите количество точек экстремума функции у =f (x) на отрезке [– 3; 7] y 4 y = f /(x) 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 -4 -5 Ответ: 3. f/(x) -8 + – + – + 8 f(x) -5 0 3 6 x
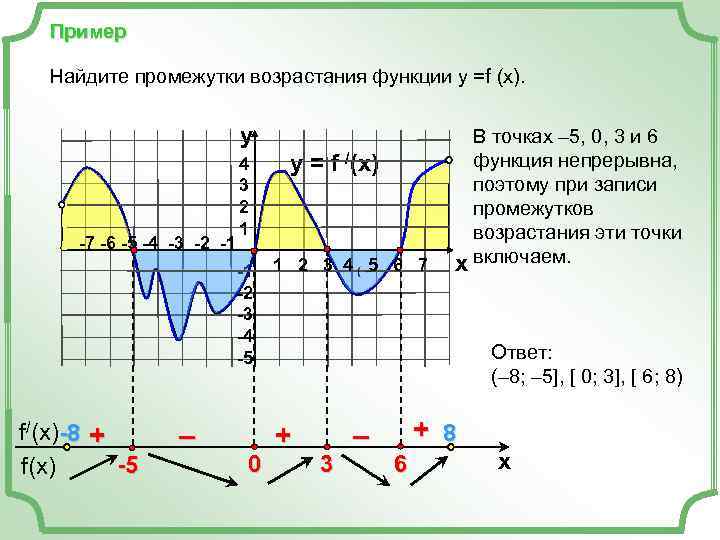
 Пример Найдите промежутки возрастания функции у =f (x). y В точках – 5, 0, 3 и 6 4 y = f /(x) функция непрерывна, 3 поэтому при записи 2 промежутков 1 возрастания эти точки -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x включаем. -2 -3 -4 -5 Ответ: (– 8; – 5], [ 0; 3], [ 6; 8) f/(x)-8 + – + 8 f(x) -5 0 3 6 x
Пример Найдите промежутки возрастания функции у =f (x). y В точках – 5, 0, 3 и 6 4 y = f /(x) функция непрерывна, 3 поэтому при записи 2 промежутков 1 возрастания эти точки -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x включаем. -2 -3 -4 -5 Ответ: (– 8; – 5], [ 0; 3], [ 6; 8) f/(x)-8 + – + 8 f(x) -5 0 3 6 x
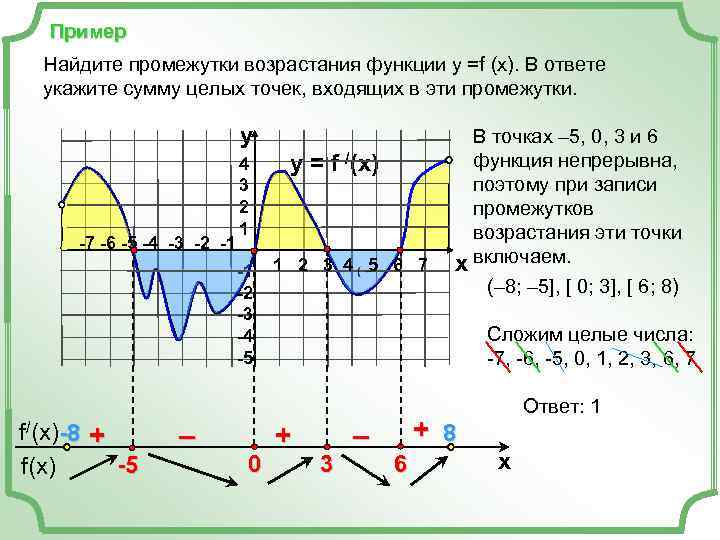
 Пример Найдите промежутки возрастания функции у =f (x). В ответе укажите сумму целых точек, входящих в эти промежутки. y В точках – 5, 0, 3 и 6 4 y = f /(x) функция непрерывна, 3 поэтому при записи 2 промежутков 1 возрастания эти точки -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x включаем. -2 (– 8; – 5], [ 0; 3], [ 6; 8) -3 -4 Сложим целые числа: -5 -7, -6, -5, 0, 1, 2, 3, 6, 7 Ответ: 1 f/(x)-8 + – + 8 f(x) -5 0 3 6 x
Пример Найдите промежутки возрастания функции у =f (x). В ответе укажите сумму целых точек, входящих в эти промежутки. y В точках – 5, 0, 3 и 6 4 y = f /(x) функция непрерывна, 3 поэтому при записи 2 промежутков 1 возрастания эти точки -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x включаем. -2 (– 8; – 5], [ 0; 3], [ 6; 8) -3 -4 Сложим целые числа: -5 -7, -6, -5, 0, 1, 2, 3, 6, 7 Ответ: 1 f/(x)-8 + – + 8 f(x) -5 0 3 6 x
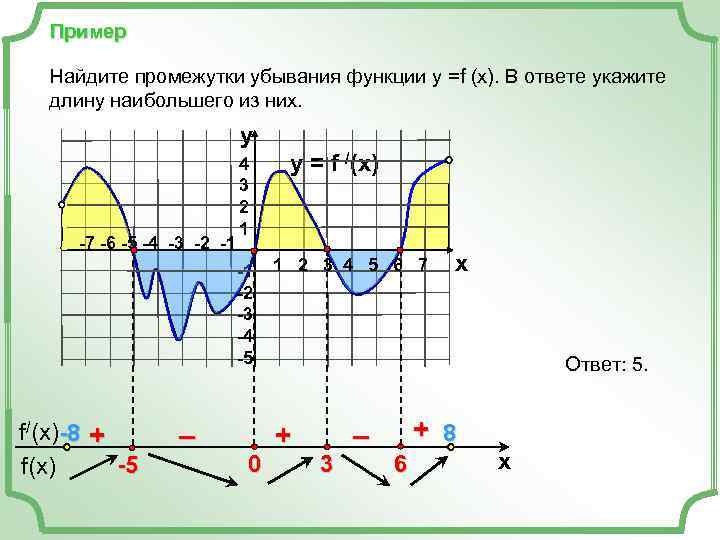
 Пример Найдите промежутки убывания функции у =f (x). В ответе укажите длину наибольшего из них. y 4 y = f /(x) 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 -4 -5 Ответ: 5. f/(x)-8 + – + 8 f(x) -5 0 3 6 x
Пример Найдите промежутки убывания функции у =f (x). В ответе укажите длину наибольшего из них. y 4 y = f /(x) 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 -4 -5 Ответ: 5. f/(x)-8 + – + 8 f(x) -5 0 3 6 x
![> Пример В какой точке отрезка [– 4; – 1] функции у =f > Пример В какой точке отрезка [– 4; – 1] функции у =f](https://present5.com/presentation/3/15595804_155010924.pdf-img/15595804_155010924.pdf-9.jpg) Пример В какой точке отрезка [– 4; – 1] функции у =f (x) принимает наибольшее значение? y На отрезке [– 4; – 1] 4 y = f /(x) функция у =f (x) 3 убывает, значит, 2 наибольшее значение 1 на данном отрезке -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 x функция будет -1 принимать в точке – 4. -2 -3 -4 -5 Ответ: – 4. f/(x)-8 + – + 8 f(x) -5 0 3 6 x
Пример В какой точке отрезка [– 4; – 1] функции у =f (x) принимает наибольшее значение? y На отрезке [– 4; – 1] 4 y = f /(x) функция у =f (x) 3 убывает, значит, 2 наибольшее значение 1 на данном отрезке -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 x функция будет -1 принимать в точке – 4. -2 -3 -4 -5 Ответ: – 4. f/(x)-8 + – + 8 f(x) -5 0 3 6 x
![> Пример В какой точке отрезка [– 4; – 1] функции у =f > Пример В какой точке отрезка [– 4; – 1] функции у =f](https://present5.com/presentation/3/15595804_155010924.pdf-img/15595804_155010924.pdf-10.jpg) Пример В какой точке отрезка [– 4; – 1] функции у =f (x) принимает наименьшее значение? y На отрезке [– 4; – 1] 4 y = f /(x) функция у =f (x) 3 убывает, значит, 2 наименьшее значение 1 на данном отрезке -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 x функция будет -1 принимать в конце -2 -3 отрезка точке х= – 1. -4 -5 Ответ: – 1. f/(x)-8 + – + 8 f(x) -5 0 3 6 x
Пример В какой точке отрезка [– 4; – 1] функции у =f (x) принимает наименьшее значение? y На отрезке [– 4; – 1] 4 y = f /(x) функция у =f (x) 3 убывает, значит, 2 наименьшее значение 1 на данном отрезке -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 x функция будет -1 принимать в конце -2 -3 отрезка точке х= – 1. -4 -5 Ответ: – 1. f/(x)-8 + – + 8 f(x) -5 0 3 6 x
![> Пример В какой точке отрезка [ 0; 3] функции у =f (x) > Пример В какой точке отрезка [ 0; 3] функции у =f (x)](https://present5.com/presentation/3/15595804_155010924.pdf-img/15595804_155010924.pdf-11.jpg) Пример В какой точке отрезка [ 0; 3] функции у =f (x) принимает наибольшее значение? y На отрезке [ 0; 3] 4 y = f /(x) функция у =f (x) 3 возрастает, значит, 2 наибольшее значение 1 на данном отрезке -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 x функция будет -1 принимать в конце -2 -3 отрезка точке х=3. -4 -5 Ответ: 3. f/(x)-8 + – + 8 f(x) -5 0 3 6 x
Пример В какой точке отрезка [ 0; 3] функции у =f (x) принимает наибольшее значение? y На отрезке [ 0; 3] 4 y = f /(x) функция у =f (x) 3 возрастает, значит, 2 наибольшее значение 1 на данном отрезке -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 x функция будет -1 принимать в конце -2 -3 отрезка точке х=3. -4 -5 Ответ: 3. f/(x)-8 + – + 8 f(x) -5 0 3 6 x
![> Пример В какой точке отрезка [ 1; 4] функции у =f (x) > Пример В какой точке отрезка [ 1; 4] функции у =f (x)](https://present5.com/presentation/3/15595804_155010924.pdf-img/15595804_155010924.pdf-12.jpg) Пример В какой точке отрезка [ 1; 4] функции у =f (x) принимает наибольшее значение? y Наибольшее значение 4 y = f /(x) на отрезке [ 1; 4] 3 функция у =f (x) будет 2 принимать в точке 1 максимума х=3. -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 -4 -5 Ответ: 3. f/(x)-8 + – + ü– 6 + 8 x f(x) -5 0 3
Пример В какой точке отрезка [ 1; 4] функции у =f (x) принимает наибольшее значение? y Наибольшее значение 4 y = f /(x) на отрезке [ 1; 4] 3 функция у =f (x) будет 2 принимать в точке 1 максимума х=3. -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 x -2 -3 -4 -5 Ответ: 3. f/(x)-8 + – + ü– 6 + 8 x f(x) -5 0 3
 Функция у = f(x) определена на промежутке (- 4; 3). На рисунке изображен график ее производной. Найдите a точку , в которой функция у = f(x) принимает наибольшее значение. хmax = 1 В этой точке 1 2 Не верно! функция у =f(x) примет y = f /(x) наибольшее Не верно! 2 -2 значение. Не верно! 3 -4 -4 -3 -2 -1 1 2 3 4 5 х Верно! 4 1 Проверка (2) f/(x) + ü– f(x) -4 1 3
Функция у = f(x) определена на промежутке (- 4; 3). На рисунке изображен график ее производной. Найдите a точку , в которой функция у = f(x) принимает наибольшее значение. хmax = 1 В этой точке 1 2 Не верно! функция у =f(x) примет y = f /(x) наибольшее Не верно! 2 -2 значение. Не верно! 3 -4 -4 -3 -2 -1 1 2 3 4 5 х Верно! 4 1 Проверка (2) f/(x) + ü– f(x) -4 1 3
 Функция у = f(x) определена на интервале (- 5; 4). На рисунке изображен график ее производной. Найдите a точку , в которой функция у = f(x) принимает наименьшее значение. хmin = 2 y Верно! В этой точке 1 2 функция y = f /(x) у =f(x) примет Не верно! наименьшее 2 0 значение. Не верно! 3 -5 -4 -3 -2 -1 1 2 3 4 5 х 4 -3 Не верно! Проверка (2) f/(x) – ü+ f(x) -5 2 4
Функция у = f(x) определена на интервале (- 5; 4). На рисунке изображен график ее производной. Найдите a точку , в которой функция у = f(x) принимает наименьшее значение. хmin = 2 y Верно! В этой точке 1 2 функция y = f /(x) у =f(x) примет Не верно! наименьшее 2 0 значение. Не верно! 3 -5 -4 -3 -2 -1 1 2 3 4 5 х 4 -3 Не верно! Проверка (2) f/(x) – ü+ f(x) -5 2 4
 На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 6; 8). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек максимума. y 4 Не верно! 3 y = f /(x) 1 7 2 1 x Верно! -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 2 3 -2 -3 Не верно! -4 3 8 -5 Не верно! 4 4 f/(x) – ü + – ü+ – + ü f(x) -5 -4 -2 1 3 4 7 Проверка (2)
На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 6; 8). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек максимума. y 4 Не верно! 3 y = f /(x) 1 7 2 1 x Верно! -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 2 3 -2 -3 Не верно! -4 3 8 -5 Не верно! 4 4 f/(x) – ü + – ü+ – + ü f(x) -5 -4 -2 1 3 4 7 Проверка (2)
 На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 5; 5). Исследуйте функцию у =f (x) на монотонность и укажите число ее промежутков убывания. y Не верно! y = f /(x) 4 1 3 2 1 Не верно! x 2 2 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 -2 Верно! -3 3 1 -4 -5 Не верно! 4 4 f/(x) + – + f(x) 1 4 Проверка (2)
На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 5; 5). Исследуйте функцию у =f (x) на монотонность и укажите число ее промежутков убывания. y Не верно! y = f /(x) 4 1 3 2 1 Не верно! x 2 2 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 -2 Верно! -3 3 1 -4 -5 Не верно! 4 4 f/(x) + – + f(x) 1 4 Проверка (2)
 На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 6; 8). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек экстремума. y 4 y = f /(x) Не верно! 3 1 5 2 1 x Верно! -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 2 2 -2 -3 Не верно! -4 3 1 -5 Не верно! 4 4 f/(x) + ü– ü + f(x) -5 -2 Проверка (2)
На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 6; 8). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек экстремума. y 4 y = f /(x) Не верно! 3 1 5 2 1 x Верно! -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 2 2 -2 -3 Не верно! -4 3 1 -5 Не верно! 4 4 f/(x) + ü– ü + f(x) -5 -2 Проверка (2)
 В. На рисунке изображен график производной функции у =f /(x), заданной на промежутке [-5; 5]. Исследуйте функцию у =f (x) на монотонность и укажите наибольшую точку максимума. Из двух точек максимума наибольшая хmax = 3 Не верно! y = f /(x) 1 5 Верно! + 1 + 2 3 4 +х 5 -4 -3 -2 -1 - 2 3 Не верно! 3 2 4 4 f ü Не верно! /(x) - + - + f(x) -4 -2 0 3 4
В. На рисунке изображен график производной функции у =f /(x), заданной на промежутке [-5; 5]. Исследуйте функцию у =f (x) на монотонность и укажите наибольшую точку максимума. Из двух точек максимума наибольшая хmax = 3 Не верно! y = f /(x) 1 5 Верно! + 1 + 2 3 4 +х 5 -4 -3 -2 -1 - 2 3 Не верно! 3 2 4 4 f ü Не верно! /(x) - + - + f(x) -4 -2 0 3 4
 На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 6; 7). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек экстремума. y 4 y = f /(x) Не верно! 3 1 8 2 1 x Верно! -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 2 4 -2 -3 Не верно! -4 3 2 -5 Не верно! 4 1 f/(x) + ü – ü + ü– ü + f(x) 1 3 5 6 5 6 Проверка (2)
На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 6; 7). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек экстремума. y 4 y = f /(x) Не верно! 3 1 8 2 1 x Верно! -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 2 4 -2 -3 Не верно! -4 3 2 -5 Не верно! 4 1 f/(x) + ü – ü + ü– ü + f(x) 1 3 5 6 5 6 Проверка (2)
 Функция у = f(x) определена на промежутке (- 6; 3). На рисунке изображен график ее производной. Найдите длину промежутка убывания этой функции. y Верно! 4 3 y = f /(x) 1 8 2 1 Не верно! x -7 -6 -5 -4 -3 -2 -1 2 6 -1 1 2 3 4 5 6 7 -2 -3 Не верно! -4 3 4 -5 4 9 Не верно! – f/(x) IIIIIIIIIIIIIIIIIII + 3 f(x)-6 2 Проверка (2)
Функция у = f(x) определена на промежутке (- 6; 3). На рисунке изображен график ее производной. Найдите длину промежутка убывания этой функции. y Верно! 4 3 y = f /(x) 1 8 2 1 Не верно! x -7 -6 -5 -4 -3 -2 -1 2 6 -1 1 2 3 4 5 6 7 -2 -3 Не верно! -4 3 4 -5 4 9 Не верно! – f/(x) IIIIIIIIIIIIIIIIIII + 3 f(x)-6 2 Проверка (2)

