Graceful Service Degradation Or How To Know Your

Graceful Service Degradation (Or, How To Know Your Payment Is Late) Alexandr Andoni (MIT) Jessica Staddon (PARC)

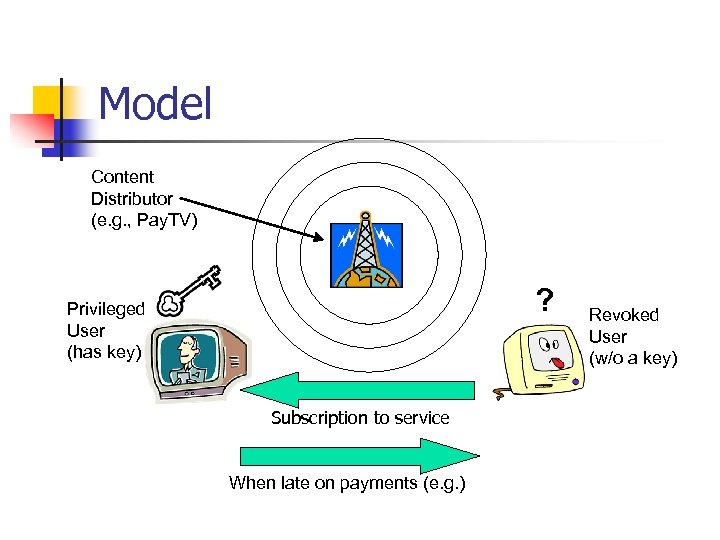Model Content Distributor (e. g. , Pay. TV) ? Privileged User (has key) Subscription to service When late on payments (e. g. ) Revoked User (w/o a key)

Problem n Transition too rigid: n n n When late on a payment (e. g. ) ? ineffective, disruptive when happened unexpectedly, in error, etc Too much if just a reminder of late payment Example scenario: n n User forgot to pay the monthly payment (or, is at the end of trial period) => is revoked by the distributor => misses favorite TV show => reinstatement: high logistical cost

Remedy n Cues on pending revocation n n I. e. , graceful revocation: n n n Graceful, but tied to the content Degrade quality of service (e. g. , content is delayed or partial) For users that are “a little late” on payment “Degradation”? n n Degraded = it takes more effort to decrypt the content; but all content is decrypted in the end (our definition) Other possible definitions (not considered here): n Video is choppy [Abdalla-Shavitt-Wool’ 03]

How… n To impose “effort to decrypt” on degraded users: via variably hard functions n n Computing the function incurs computational effort The amount of computational effort is parametrizable Inspired by hard functions from spam-fighting, “pricing functions” [Dwork-Naor’ 92], “proofs of work” [Jakobsson. Juels’ 03], others To segregate users into classes: via degradation protocols n n Degradation protocol = variation of revocation protocol Revocation protocol = allows targeting content to any set P of users

Variably Hard Functions n From “proofs of work” for fighting spam: n For an email m, have to attach F(m) such that: n n n “Moderately hard” to compute F(m) (e. g. , 10 secs) Easy (fast) to check that is valid We need: n Parametrizable “moderately hard” function F n n A degraded user gets “m” and a hardness parameter p Computing F(m) takes roughly O(2 p) operations

Def: Variably Hard Functions n F( • ) is variably hard if: n When user receives n n n Can’t compute n n n Test value g(x*), together with g( • ) Hint: a set Y(p)(x*) containing x*; size of the set =2 p F(x*) in less than ~O(2 p) operations “Hardness” is in not knowing x* But can compute F(x*) in O(2 p): n Try all possible x Y(p)(x*) until g(x)=g(x*)

Example: F based on OWP n n P = one-way permutation Define n g(x)=P(x) n F(x)=x Thus, F(x)=P-1(g(x)) A hint Y(p)(x*): some bits of x* k bits x*= 01001… 11010. . . Y(p)(x*)= 01001… *****. . . p bits n In paper: memory-bound functions [Dwork-Goldberg-Naor’ 03] n An operation = an access to main memory

Using Variably Hard Functions n n n Encrypt the content with a session key SK=F(x*) Broadcast g(x*) Distribute hints of x* using revocation protocol Class of users Hint received Time to compute SK P, privileged users Complete Fast: O(1) D, degraded users Partial Moderate: O(2 p) R, revoked users Impossible: O(2 k) No hint Hint given to P x*= Hint given to D

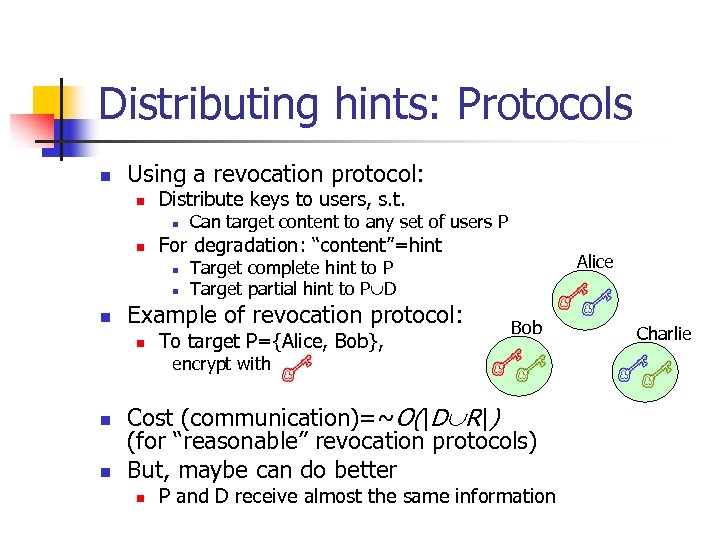Distributing hints: Protocols n Using a revocation protocol: n Distribute keys to users, s. t. n n For degradation: “content”=hint n n n Can target content to any set of users P Example of revocation protocol: n Alice Target complete hint to P Target partial hint to P D To target P={Alice, Bob}, Bob encrypt with n n Cost (communication)=~O(|D R|) (for “reasonable” revocation protocols) But, maybe can do better n P and D receive almost the same information Charlie

Improved protocol n n Proof of concept: will modify revocation protocol of [Kumar-Rajagopalan-Sahai’ 99] 2 steps: n in R 1. cover free families n n U n Let U be a universe of keys A user u gets a Su U, |Su|=s To broadcast message SK to only P: n Take U n n in P n Throw away all keys known by R For each remaining key k, broadcast Ek[SK] Design sets Su such that: n Each user in P can decrypt at least s/2 copies of SK

Revocation: Step 2 n 2. secret sharing n n n Improves on 1 st step Can improve because a u P gets s/2 copies of SK Use secret sharing scheme n n n Create |U| shares of SK Such that s/2 shares are enough to recover SK Improved parameters [KRS’ 99, randomized]: n Communication blowup: reduced to O(r) from O(r 2*log n)

Towards degradation protocol n n So far, [KRS’ 99] establishes: n If u P, then gets s/2 shares of SK n If u R, then gets 0 shares Would like: n If u P, then gets s/2 shares of SK n If u D, then gets f*s/2 shares (0

Degradation protocol: Result n n Can improve bounds (over those of the revocation protocol) But messy: many parameters (max # revoked, max # degraded, hardness parameter) Have to know all the parameters in advance (as for KRS’ 99) Not collusion resistant against degraded users n n Several degraded users may have sufficient # of shares However, practical argument: not a “serious” problem n n Degradation mainly serves as a cue Act of colluding is sufficient to serve as a cue

More degradation protocols n Observations: n n Not necessary to redistribute hints for each new session if user classes don’t change Want finer division into classes: n n Privileged class P Degraded classes D 1, D 2, … DL (with progressively worse service quality) Revoked class R Known degradation schedule: we may know when a user will be degraded

Degradation Protocol 2 n Will present: Known degradation schedule n n Trial period scenario General scenario (unknown schedule): similar, but need to use revocation protocols

Trial Period Scenario: Model normal service t=0 (subscription) n n n degraded t=30 t=40 revoked time In the period 30 th -> 40 th day, the service is progressively worse 1 degraded class per day: D 1, D 2, …D 10 Each Di has its “hardness” parameter

Trial Period Scenario: Construction n n Broadcast on day t: EF(x)[SK], g(x) Hints: n n Construct Ai , where Ai=W(Ai+1) and W is OWP Give A 29 to user On day t<30, the user has complete hint x On day t≥ 30, the user has partial hint on x ←A 19←A 20←A 21←… At t=29, x= At t=30, x= At t=31, x= ←A 29←A 30←A 31←… … … Legend: ← means application of a OWF/OWP ? … … ? ?

Conclusions n Introduced the notion of service degradation n n Degraded users: between privileged and revoked (service-wise) Have degraded service quality Serves as a cue to impending revocation Construction based on: n n Variably hard functions Revocation protocols

Questions (for Lunch-Break) n Degradation: n n How much can it buy us in terms of user storage and communication? (over revocation) We define “degradation”=delay. Is this the right approach? Are there other (better) ones that we can provably impose on degraded users, without losing in performance?

Thank you!