Имитац моделир.ppt
- Количество слайдов: 21

Государственное образовательное учреждение высшего профессионального образования Академия народного хозяйства при Правительстве Российской Федерации ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ Имитационное моделирование бизнес-процессов Тема № 3 «Моделирование случайных событий и величин» Кафедра системного анализа и информатики

1 ВОПРОСЫ ЛЕКЦИИ 1. 2. 3. Моделирование случайных событий и величин. Управление модельным временем. Моделирование параллельных процессов. Виды параллельных процессов в сложных системах.
2 1. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ СОБЫТИЙ И ВЕЛИЧИН. Имитационное моделирование – это численный метод исследования систем и процессов с помощью моделирующего алгоритма Возможности Matlab по моделированию случайных величин и процессов (раздел Toolboxes - Statistics - Random - Number Generation)

3 где , - очередное и предыдущее случайные числа соответственно; В основе всех методов и приемов моделирования случайных событий и величин Достоинство метода заключается в том, что при одних и тех же значениях А, С – константы лежит использование случайных чисел, имеющих равномерное распределение на входящих в выражение (1) величин можно полностью воспроизвести эксперимент. М – достаточно большое целое положительное число (чем больше М, тем длиннее интервале [0; 1]. (1) неповторяемая последовательность)

4 ОСНОВНЫЕ АНАЛИЗИРУЕМЫЕ ХАРАКТЕРИСТИКИ ГЕНЕРИРУЕМЫЕ ДАТЧИКОМ ПОСЛЕДОВАТЕЛЬНОСТЕЙ: ü- равномерность; ü- стохастичность; ü- независимость. 1. Проверка равномерности может быть выполнена с помощью гистограммы относительных частот, генерируемой СВ.

5 2. Проверка стохастичности. xi - достаточно большая последовательность случайных чисел где - число комбинаций (сочетаний) j единиц в l разрядах; N – длина выборки - вероятность появления единицы в двоичном разряде, р(1)=0, 5. l – старший разряд чисел j- количество единиц Тогда ожидаемое число появлений случайных чисел xi с j единицами при длине выборки N:

6 3. Проверка независимости. Проводится на основе вычисления корреляционного момента. А) Вводят в рассмотрение дополнительную последовательность Y, в которой yi = x 1 +t, где t – величина сдвига последовательности Y относительно исходной последовательности X. Б) Вычисляют коэффициент корреляции случайных величин Х и Y, для чего используют специальные расчетные соотношения. Моделирование случайных событий А – случайное событие; Рс – вероятность случайного события; r – число; [0; 1] – интервал, на котором равномерно распределено число r.

7 Для моделирования полной группы N несовместных событий A={A 1, A 2, A 3, …, AN} с вероятностями соответственно Р 1, Р 2, …, РN достаточно одного значения r. Событие Аi из группы А считается наступившим, если выполняется условие: Если группа событий А не полна, то вводят фиктивное событие АN+1 с вероятностью РN+1, такой, что то есть дополняют группу А до полной.

8 Моделирование дискретных случайных величин Используются 2 метода: • метод последовательных сравнений; • метод интерпретации. 1. Метод последовательных сравнений. Число r сравнивают со значением суммы Р 1+Р 2+…, где Р 1 – вероятность наименьшего значения СВ Y, Р 2 - вероятность второго по величине значения. Проверка прекращается и дискретная СВ Y считается принявшей значение уi

9 2. Метод интерпретации. Основан на физической трактовке моделируемого закона распределения. Например, биноминальное распределение описывает число успехов в n независимых испытаниях с вероятностью успеха в каждом испытании Р и вероятностью неудачи g=1 -P. Моделирование непрерывных случайных величин Используются три метода: • метод нелинейных преобразований; • метод композиций; • табличный метод. показательный закон распределения где λ – параметр показательного распределения, r – равномерно распределенное СЧ

10 нормальный закон распределения где m, s – параметры нормального распределения, ri – равномерно распределенное СЧ

11 При разработке практически любой имитационной модели и планировании 2. УПРАВЛЕНИЕ МОДЕЛЬНЫМ ВРЕМЕНЕМ. проведения модельных экспериментов необходимо соотносить между собой три представления времени: q реальное время, в котором происходит функционирование имитируемой системы; q модельное (системное) время, в масштабе которого организуется работа модели; q машинное время, отражающее затраты времени ЭВМ на проведение имитации. Задачи, решаемые с помощью механизма модельного времени: üотображается переход моделируемой системы из одного состояния в другое; üпроизводится синхронизация работы компонент модели; üизменяется масштаб времени «жизни» (функционирования) исследуемой системы; üпроизводится управление ходом модельного эксперимента; üмоделируется квазипараллельная реализация событий в модели. Методы реализации механизма модельного времени: - с постоянным шагом; - по особым состояниям

12 1. С постоянным шагом. Отсчет системного времени ведется через фиксированные, выбранные исследователем интервалы времени. События в модели считаются наступившими в момент окончания этого интервала. Погрешность в измерении временных характеристик системы в этом случае зависит от величины шага моделирования Δt. Метод предпочтительнее, если: - события появляются регулярно, их распределение во времени достаточно равномерно; - число событий велико и моменты их появления близки; - невозможно заранее определить моменты появления событий. Метод достаточно просто реализовать в том, случае, когда условия появления событий всех типов в модели можно представить как функцию времени.
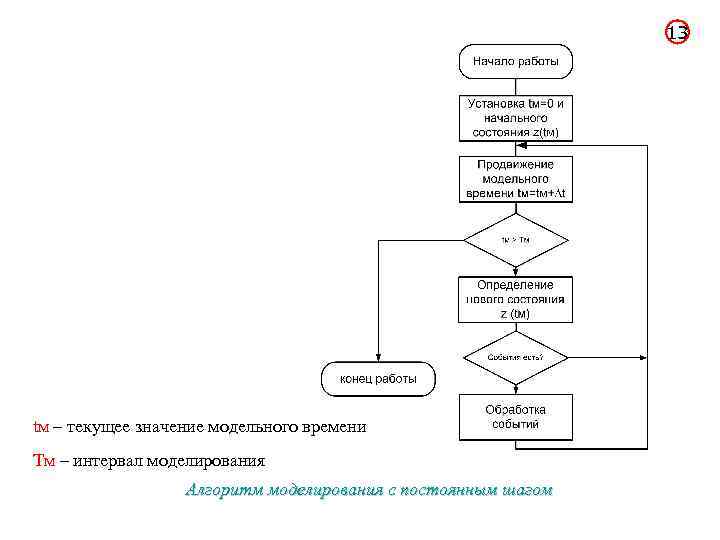
13 tм – текущее значение модельного времени Tм – интервал моделирования Алгоритм моделирования с постоянным шагом
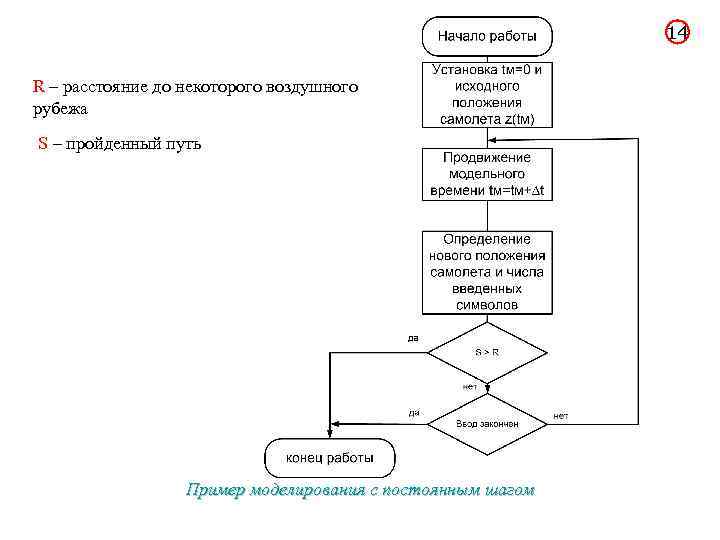
14 R – расстояние до некоторого воздушного рубежа S – пройденный путь Пример моделирования с постоянным шагом
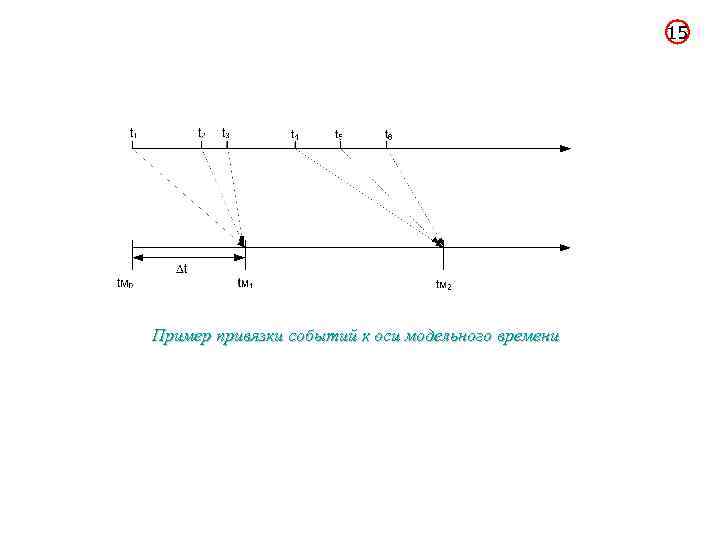
15 Пример привязки событий к оси модельного времени

16 2. По особым состояниям Системное время каждый раз изменяется на величину, строго соответствующую интервалу времени до момента наступления очередного события. В этом случае события обрабатываются в порядке их поступления, а одновременно наступившими считаются только те, которые являются одновременными в действительности. Метод целесообразно использовать, если: - события распределяются во времени неравномерно или интервалы между ними велики; - предъявляются повышенные требования к точности определения взаимного положения событий во времени; - необходимо реализовать квазипараллельную обработку одновременных событий. Достоинство метода – позволяет экономить машинное время, особенно при моделировании систем периодического действия, в которых события длительное время могут не наступать.
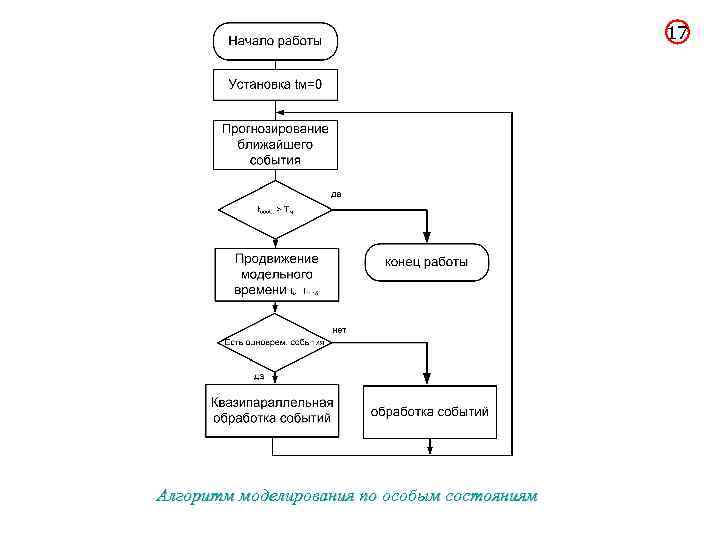
17 Алгоритм моделирования по особым состояниям
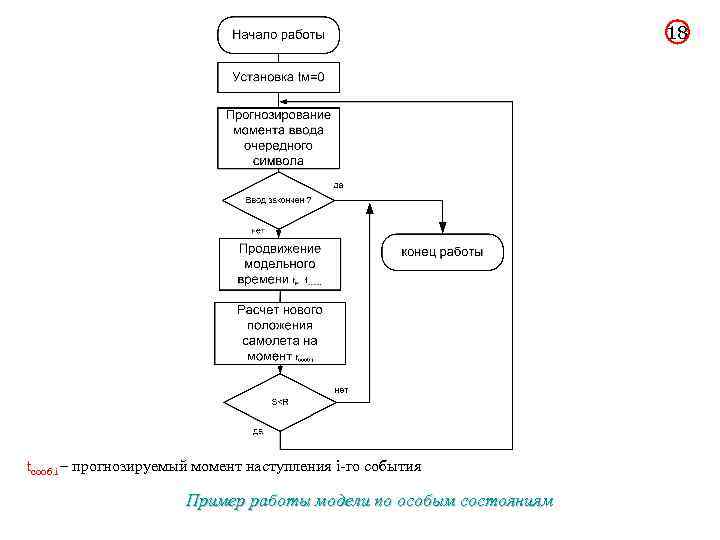
18 tсооб. i – прогнозируемый момент наступления i-го события Пример работы модели по особым состояниям

19 3. МОДЕЛИРОВАНИЕ ПАРАЛЛЕЛЬНЫХ ПРОЦЕССОВ. ВИДЫ ПАРАЛЛЕЛЬНЫХ ПРОЦЕССОВ В СЛОЖНЫХ СИСТЕМАХ. Асинхронный параллельный процесс – процесс, состояние которого не зависит от состояния другого параллельного процесса (ПП). Синхронный параллельный процесс – процесс, состояние которого зависит от состояния взаимодействующих с ним ПП. Подчиненный параллельный процесс – создается и управляется другим процессом (более высокого уровня). Независимый параллельный процесс – не является подчиненным ни для одного из процессов. Способ организации ПП в системе зависит от физической сущности этой системы. Разработка и использование любой ИМ предполагает ее программную реализацию и исследование с применением ЭВМ.

20 Особенности реализации параллельных процессов: qна уровне задач вычислительные процессы могут быть истинно параллельными только в многопроцессорных ВС или вычислительных сетях; qмногие ПП используют одни и те же ресурсы; qв ВС дополнительно используются еще два вида ПП: родительский и дочерний; особенность их состоит в том, что процесс-родитель не может быть завершен, пока не завершатся дочерние процессы. Подходы в организации параллельных процессов: qна основе «взаимного исключения» ; qна основе синхронизации посредством сигналов; qна основе обмена информацией (сообщениями) «Взаимное исключение» - предполагает запрет доступа к общим ресурсам (общим данным) для всех ПП, кроме одного, на время его работы с этими ресурсами (данными). Синхронизация – обмен сигналами между двумя и более процессами по установленному протоколу
Имитац моделир.ppt