Google nanofem platform A Software Platform for Nanoscale

Google: "nanofem platform" A Software Platform for Nanoscale Device Simulation and Visualization Marek Gayer and Giuseppe Iannaccone ACTEA 2009 - Conference on Advances in Computational Tools for Engineering Applications Notre Dame University, Faculty of Engineering,

Google: "nanofem plaform" Goals of Nano. FEM platform n Create software platform for Technology CAD device simulation based on FEM n Should be flexible & modifiable (research) n Interactive features: Geometry, meshing and visualization with user interface n Separation of IT (software) and physics n Ability to run simulations on remote servers n Able to run on Windows, Linux, Mac OS X n Extendible; users should be able to develop for the platform writing own modules n Performance ACTEA 2009 2

Google: "nanofem plaform" Finite Element Method n Finding solution for Partial n n ACTEA 2009 Differential equations for evaluation of characteristics (e. g. potential) Discretizes continuum (i. e. modeled object) into finite number of elements – e. g. triangles, tetrahedron Characteristics are determined in the nodes of the element Solving of linear systems Complex to design and implement, solid mathematical and informatics understanding required for high performance 3

Google: "nanofem plaform" 3 D Finite Element Mesh n Suitable discretization of continuous domain to simple volume cell elements n Partial differential equations (PDE’s) can be replaced by system of non-linear algebraic equations n Very complex to create code to generate FEM mesh on arbitrary structures n Mesh need to be at least Delaunay mesh n Tetrahedrons ACTEA 2009 4

Google: "nanofem plaform" Related solutions / approaches n Commercial codes (Synopsis, Silvaco, etc. ) n Disadvantages: limited extendibility, modifications n Free codes 2 D, 3 D: – Archimedes, nextnano n Free Meshers - NETGEN, Tetgen n Existing simulation frameworks – Gmsh, Calculix, Salome Platform, Orcan, n Finite Element Solvers – FEni. CS/DOLFIN, Libmesh, Getfem++, Rheolef, Tahoe, OOFEM. org, OFELI ACTEA 2009 5

Google: "nanofem plaform" Transistor modeled in NETGEN ACTEA 2009 6

Google: "nanofem plaform" Gmsh – Mesh of transistor + Postprocessing (tutorial dataset) ACTEA 2009 7

Google: "nanofem plaform" Components of Nano. FEM platform n SALOME 3. 2. 6 supports limited number of OS’s => n Developed as a Vm. Ware image with: – Debian Linux 3. 1 (codename Sarge) – SALOME 3. 2. 6 – FEni. CS/DOLFIN 0. 7. 1 – Mesh. API – lib. for our FEM module/component – Component and additional codes for SALOME – KDevelop for development – Additional tools (Krusader, …) n Running on Vm. Ware Server 1+ or Workstation 6+ n Eventual distribution by providing this Vm. Ware image ACTEA 2009 8

Google: "nanofem plaform" Nano. FEM platform modelling approach Salome Platform Mesh. API with DOLFIN/FEni. CS ACTEA 2009 9

Google: "nanofem plaform" SALOME platform (LGPL) www. salome-platform. org n SALOME(LGPL) is a free software that provides a n n n n ACTEA 2009 generic platform for Pre and Post-Processing for numerical simulation. Interactice geometry modelling, meshing Very good user interface (Qt 4) Visualization (2 D and 3 D graphs) Can use Python scripting to replace or assist GUI: all functionalities are also accessible through the programmatic integrated Python console Modular architecture, we can create own modules Components can run on remote servers (CORBA) Exchanging data: MEDMEM API, . HDF, . MED Much more powerful then any other open source finite element component/software we found 10

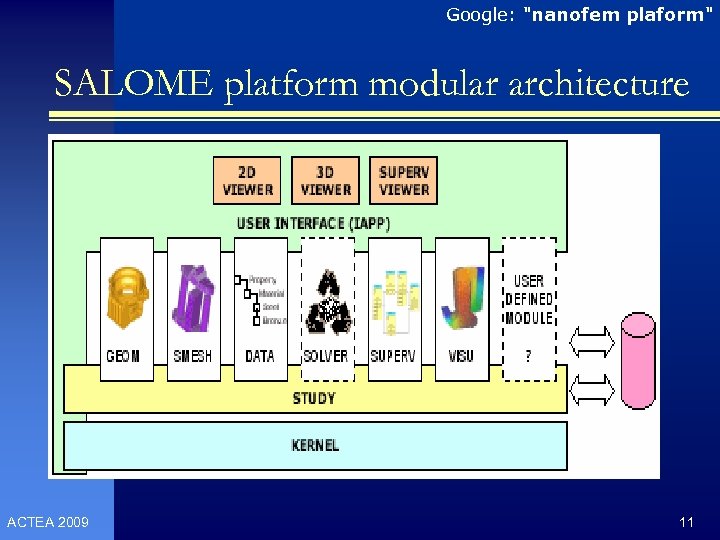Google: "nanofem plaform" SALOME platform modular architecture ACTEA 2009 11

Google: "nanofem plaform" FEni. CS/ DOLFIN – (L)GPL www. fenics. org n Free finite element library and solver n Supports both direct and iterative solvers n n n ACTEA 2009 (LU, Krylov solvers) Uses PETSc and u. BLAS libraries for systems of linear/nonlinear equations => high performance linear algebra Automatic generation of finite elements, evaluation of variational form assembly of matrices for FEM – linear systems Support for general families of finite elements, (Lagrange, BDM, RT, BDFM Nedelec and Crouzeix-Raviart elements) No deeper knowledge about FEM method is needed to use and develop Eigenvalue problems with SLEPSc Simple and intuitive C++ object interface 13

Google: "nanofem plaform" Our SALOME/DOLFIN bridge Mesh. API n Core – mesh, fields, groups n Linear-Nonlinear PDE classes n Selection from Krylov solver methods and preconditioners n XML material database (SAX parser) n Boundary conditions n Inherited Mesh. API based solvers n Wrappers for SALOME platform ACTEA 2009 15

Google: "nanofem plaform" Mesh. API – mesh, fields, groups n Reading Salome mesh from files. med files n n n n ACTEA 2009 (MEDMEM API) Processing mesh coordinates and connectivities Processing groups of mesh (can be defined in SALOME editor) Passing this information to DOLFIN (to build mesh in memory) Providing core fields (such as Source, Flux, Potential, some visual debug fields) Additional methods to work with mesh and fields Control of storing of core and custom fields to. MED files Clean code design in strictly object oriented C++ 16

Google: "nanofem plaform" Example of XML material database n n n n 17

Google: "nanofem plaform" Storing materials and boundary conditions in MEDMEM mesh n Implemented by correct naming of groups, which are then read in code to retrieve materials and boundary conditions n Examples: bottomoxide[Si] metalplate 1[dirichlet=1. 0] n From SALOME mesh, we get ID’s of nodes and assign a group color number to them n From group number, we determine material, Dirichlet boundary conditions etc. These data are stored in numeric arrays [0. . n] – n is number of groups ACTEA 2009 18

Google: "nanofem plaform" Mesh. API/Linear-Nonlinear PDE n Classes allowing solving nonlinear and nonlinear PDE, using DOLFIN, allows to set preconditioners and Krylov methods: n Available Krylov methods: – cg - The conjugate gradient method – gmres - The GMRES method (default) – bicgstab - The stabilized biconjugate gradient squared method n Preconditioners: – none - No preconditioning – jacobi - Simple Jacobi preconditioning – sor - SOR, successive over-relaxation – ilu - Incomplete LU factorization (default) – icc - Incomplete Cholesky factorization – amg - Algebraic multigrid (through Hypre when available) ACTEA 2009 19

Google: "nanofem plaform" Mesh. API based solvers n Using Mesh. API, one can easily, in few lines define DOLFIN solvers as classes inherited from cl. Dolfin n Behaviour that can be generalized and reused is already defined in Mesh API n It can be used in any current and future examples n There are 3 example solvers: – Poisson example from DOLFIN manual, but using Salome mesh – Poisson equation computed on partitioned group with permittivity (Eps) – Non-linear Poisson equation computed on partitioned group with permittivity (not 100% done) ACTEA 2009 20

Google: "nanofem plaform" Solving example – linear Poisson n Solving linear PDE: Poisson equation: n f(x, y, z) – source function (known), can be 0 n ε(x, y, z) – permittivity of material in given point n u(x, y, z) – potential, that we are computing ACTEA 2009 21

Google: "nanofem plaform" Solving example – linear Poisson n Bi-linear and linear form of Poisson equation: n g(x, y, z) – Neumann boundary condition ACTEA 2009 22

Google: "nanofem plaform" Converting equation to variational form n # The bilinear form a(v, U) and linear form L(v) for n # Poisson's equation. n # Compile this form with FFC: ffc -l dolfin Poisson. Eps. form n n n element = Finite. Element("Lagrange", "tetrahedron", 1) v = Test. Function(element) u = Trial. Function(element) f = Function(element) g = Function(element) eps = Function(element) n a = dot(grad(v), grad(u))*eps*dx n L = v*f*dx + eps*v*g*ds n # This generates 5239 lines, 191. 359 characters ACTEA 2009 23

Google: "nanofem plaform" Main solving routine in C++ n n ACTEA 2009 #include "Poisson. Eps. h“ #include "Linear. PDE. hxx" int SC: : Poisson. Eps: : solve () { – Source f (mesh); – Flux g (mesh); – Dirichlet. Function u 0 (mesh); – Dirichlet. Boundary boundary(mesh); – Dirichlet. BC bc (u 0, mesh. dolfin. Mesh, boundary); – Eps eps (mesh); – Poisson. Eps. Bilinear. Form a (eps); – Poisson. Eps. Linear. Form L (f, g, eps); – SC: : Linear. PDE pde (a, L, mesh. dolfin. Mesh, bc); – pde. setup. Krylov (mesh. krylov. Method, mesh. krylov. Pc); – Function solution; – pde. solve(solution); n } – mesh. node. Potential. init (u); mesh. node. Source. init (f); mesh. node. Flux. init (g); – mesh. reset. Fields. To. Write(); – Field *fields[] = {&mesh. node. Potential, &mesh. node. Source, &mesh. node. Flux, NULL}; – mesh. add. Fields. To. Write (fields); 24

Google: "nanofem plaform" Dirichlet boundary in C++ n class Dirichlet. Boundary : public Sub. Domain n { – Mesh. API &mesh; public: – Dirichlet. Boundary(Mesh. API & mesh. Instance) : mesh(mesh. Instance) – { – } – bool inside(const dolfin: : real* x, bool on_boundary) const – { int index = mesh. get. Group. Number. From. Coordinates(x); Material. Function *node. Material = mesh. material. Functions[index]; return node. Material->material. Data == NULL; } }; ACTEA 2009 25

Google: "nanofem plaform" Dirichlet values in C++ n class Dirichlet. Function : public Function n { – Mesh. API &mesh; public: – Dirichlet. Function(Mesh. API& mesh. Instance) : mesh(mesh. Instance), Function(mesh. Instance. dolfin. Mesh) – { – } – dolfin: : real eval(const dolfin: : real* x) const – { – int index = mesh. get. Group. Number. From. Coordinates(x); Material. Function *node. Material = mesh. material. Functions[index]; – return node. Material->dirichlet; – } }; ACTEA 2009 26

Google: "nanofem plaform" Source function in C++ n class Source : public Function n { – Mesh. API &mesh; public: ACTEA 2009 – Source(Mesh. API & mesh. Instance) : mesh(mesh. Instance), Function(mesh. Instance. dolfin. Mesh) –{ –} – dolfin: : real eval(const dolfin: : real* x) const –{ v return 0; –} }; 27

Google: "nanofem plaform" Neumann boundary conditions C++ n class Flux : public Function n { – Mesh. API &mesh; public: ACTEA 2009 – Flux(Mesh. API & mesh. Instance) : mesh(mesh. Instance), Function(mesh. Instance. dolfin. Mesh) –{ –} – dolfin: : real eval(const dolfin: : real* x) const –{ v return 0; –} }; 28

Google: "nanofem plaform" Defining permittivity in C++ n class Eps : public Function n { – Mesh. API &mesh; public: – Eps (Mesh. API& mesh. Instance) : mesh(mesh. Instance), Function(mesh. Instance. dolfin. Mesh) – { – } – dolfin: : real eval(const dolfin: : real* x) const – { – int index = mesh. get. Group. Number. From. Coordinates(x); Material. Function *node. Material = mesh. material. Functions[index]; – return node. Material->permitivity; – } }; ACTEA 2009 29

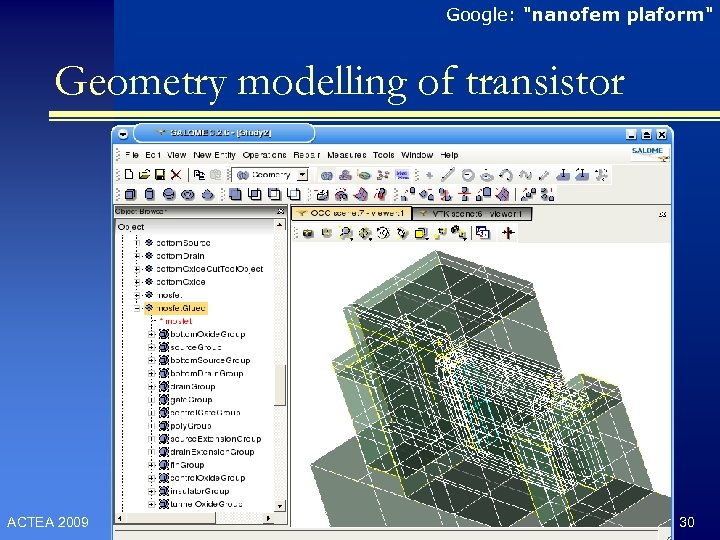Google: "nanofem plaform" Geometry modelling of transistor ACTEA 2009 30

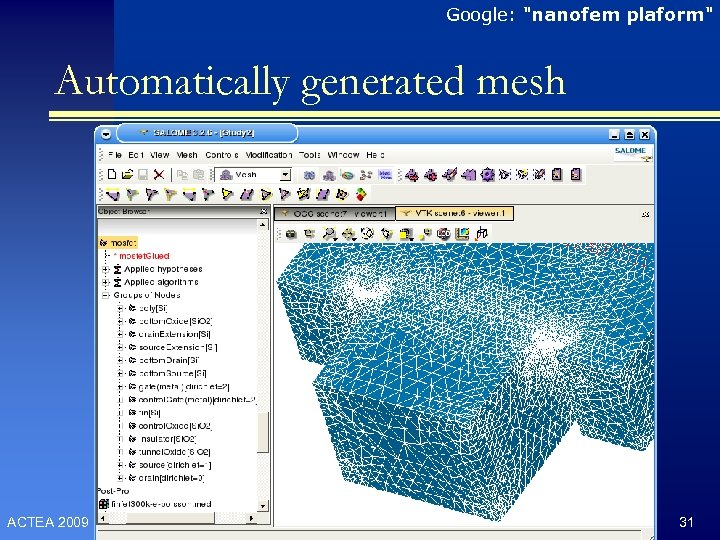Google: "nanofem plaform" Automatically generated mesh ACTEA 2009 31

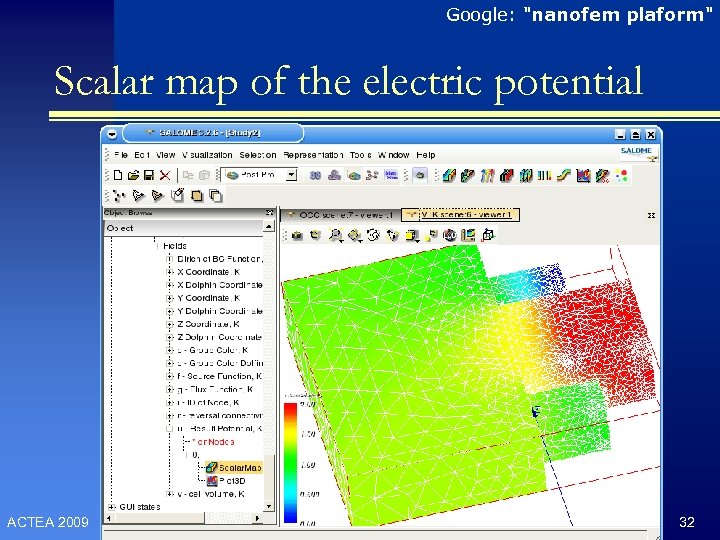Google: "nanofem plaform" Scalar map of the electric potential ACTEA 2009 32

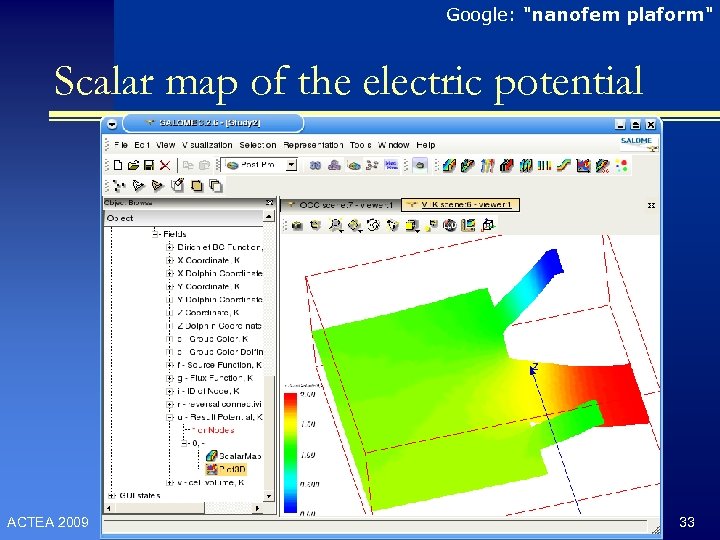Google: "nanofem plaform" Scalar map of the electric potential ACTEA 2009 33

Google: "nanofem plaform" Conclusion - 1/2 n Nano. FEM platform is a new research environment for TCAD simulations of nanoscale devices. n Based on free LGPL components SALOME Platform and FEni. CS/DOLFIN n We can concentrate only on developing of our Mesh. API and computational modules n Physicist/developers – independent n Simple definition of equations instead of programming ACTEA 2009 34

Google: "nanofem plaform" Conclusion – 2/2 n Interactive pre- and post-processing n Automated meshing n Modules can run on remote servers n High performance n Standard formats -. MED and. HDF n. XML material database n Good extendibility and modularity ACTEA 2009 35

Google: "nanofem plaform" Possible future effort for the Nano. FEM Platform n More complex equations (drift, diffusion) n Compare performance with commercial n More modules with exchange of fields n Control of simulation flow and coupling n Tests of supervision (with scripting) n More complex boundary conditions n Run on native Debian and Windows ACTEA 2009 36

Google: "nanofem plaform" Thank you for your attention. ? ? ? ACTEA 2009 Do you have any questions ? 37