Goldman Sachs Co Controllers University Capital Markets

Скачать презентацию Goldman Sachs Co Controllers University Capital Markets

4d234030dc341ea22a88678805c91078.ppt

Количество слайдов: 98

Goldman, Sachs & Co. Controllers University Capital Markets Curriculum Module 2: Session 5 Bond Structures: Calls, Puts, and Structured Notes Alan L. Tucker, Ph. D. 631 -331 -8024 (tel) 631 -331 -8044 (fax) tucker@mtaglobal. com Copyright © 2000 -2001 Marshall, Tucker & Associates, LLC All rights reserved 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 1

ALAN L. TUCKER, Ph. D. Alan L. Tucker is Associate Professor of Finance at the Lubin School of Business, Pace University, New York, NY and an Adjunct Professor at the Stern School of Business of New York University, where he teaches graduate courses in derivative instruments. Dr. Tucker is also a principal of Marshall, Tucker & Associates, LLC, a financial engineering and derivatives consulting firm with offices in New York, Chicago, Boston, San Francisco and Philadelphia. Dr. Tucker was the founding editor of the Journal of Financial Engineering, published by the International Association of Financial Engineers (IAFE). He presently serves on the editorial board of Journal of Derivatives and the Global Finance Journal and is a former associate editor of the Journal of Economics and Business. He is a former director of the Southern Finance Association and a former program co-director of the 1996 and 1997 Conferences on Computational Intelligence in Financial Engineering, co-sponsored by the IAFE and the Neural Networks Council of the IEEE. Dr. Tucker is the author of three books on financial products and markets: Financial Futures, Options & Swaps, International Financial Markets, and Contemporary Portfolio Theory and Risk Management (all published by West Publishing, a unit of International Thompson). He has also published more than fifty articles in academic journals and practitioner-oriented periodicals including the Journal of Finance, the Journal of Financial and Quantitative Analysis, the Review of Economics and Statistics, the Journal of Banking and Finance, and many others. Dr. Tucker has contributed to the development of theory of derivative products including futures, options and swaps, and to theory of international capital markets and trade. He has also contributed to theory of technology adoption over the life-cycle. The Social Sciences Citation Index shows that his research has been cited in refereed journals on over one hundred occasions. As a consultant, Dr. Tucker has worked for The United States Treasury Department, the United States Justice Department, Morgan Stanley Dean Witter, Union Bank of Switzerland, LG Securities (Korea), and Chase Manhattan Bank. Dr. Tucker holds the B. A. in economics from La. Salle University (1982), and the MBA (1984) and Ph. D. (1986) in finance from Florida State University. He was born in Philadelphia in 1960, is married (Wendy) and has three children (Emily, 1993, Michael and Matthew, both 1995). 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 2

Introduction to Structured Notes What are Structured Notes? Structured notes are hybrid securities that combine elements of derivative instruments with elements of straight debt instruments. Structured notes are a subset of a broader class of instruments known as structured securities. By combining straight debt with various forms of derivatives, it is possible to create “debt-like” instruments (the notes) that contain equity-like components, dual currency components, commodity components, and various option-like components. The straight debt components include fixed rate debt and floating rate debt. The derivatives components include options, forwards, and swaps, any one of which can be written on interest rates, exchange rates, commodity prices, or equity indexes. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 3

Introduction to Structured Notes What economic function do structured notes serve? Structured notes can be tailor-made to suit an amazing array of investor needs or preferences while at the same time satisfying the needs of issuers, even when the needs of the issuers differ significantly from the needs of the investors. Thus structured notes make it possible to more efficiently connect the suppliers of capital (i. e. , investors) with the users of capital (i. e. , investors). The efficient allocation of capital is the primary function of the financial system. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 4

Introduction to Structured Notes Who are the issuers of structured notes? : While any user of capital is a potential issuer of structured notes, Government Sponsored Enterprises (GSEs) have been the biggest issuers, followed by large corporations. Banks too have been issuers, but often in the form of structured-notelike products, such as equity-linked CDs. As one example, as far back as November 1994, The Federal Home Loan Bank (FHLB), one of the largest U. S. issuers, had issued structured notes linked to over 175 indices or index combinations. Other GSEs that are big issuers include FNMA, SLMA, and FHLMC. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 5

Introduction to Structured Notes Why have structured notes become popular? : Investors are drawn to structured notes for a variety of reasons. Their popularity grew rapidly in the early 1990 s in response, in part, to very low interest rates and very attractive returns in other markets (particularly equities). The desire to earn higher returns in a low-interest rate environment induces investor to take on risks ordinarily associated with other asset classes. At the same time, because many structured notes are issued by Government Sponsored Enterprises (GSEs), they are perceived to have very low credit risk. It is important, however, for investors to appreciate that the issuances of GSEs are not (generally) backed by the full faith and credit of the United States, the way Treasurys are. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 6

Introduction to Structured Notes Another reason these instruments have become popular is that they can be structured to offset (i. e. , hedge) unique risks that an investor faces in other asset classes. Finally, structured notes can allow an investor to play an unusual view: such as a specific benchmark interest rate staying within a prescribed range, or a particular currency or commodity rising in value, or even a flattening or steepening of the yield curve. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 7

Introduction to Structured Notes Who are the investors in structured notes? : Structured notes are generally issued in minimum denominations that are significantly larger than the minimum denominations for straight debt. For example, the FHLB issues straight debt in minimum denominations of $10, 000. For its structured securities, the minimums are generally $100, 000 and for some issuances (generally more highly structured notes) the minimums can be as high as $500, 000. These kinds of denominations suggest that investors consist, primarily, of institutions and wealthy individuals. Indeed, many structured notes are sold through private placements and can only be sold to qualified investors. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 8

Introduction to Structured Notes Retail: Despite the fact that many structured securities are intended for sale to institutional investors and wealthy individuals, some products--particularly those issued in more recent years--have been offered in denominations that appeal to retail investors. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 9

Introduction to Structured Notes The Fed’s and SEC’s concerns: During the Spring and Summer of 1994, several money market mutual funds--most notably the Piper Jaffray MMF--suffered significant losses on some structured securities that they held in their money fund portfolio. The result of these losses was to cause the NAV of the fund to drop below $1. 0. This is called “breaking the buck” and is one of the worst things (from an investor psychology perspective) that can happen to a MMF. These losses led to heightened concern on the part of the Fed, the SEC, the Office of the Comptroller of the Currency (OCC), and the Office of Thrift Supervision (OTS). 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 10

Introduction to Structured Notes Types of Structured Notes (sampling only): – Floating Interest Rate Structures: • Straight Floaters • Capped Floaters • Collared Floaters • Range Floaters • Inverse Floaters • CMT Floaters • Dual Index Floaters • Leveraged and Deleveraged Floaters – Fixed Rate Structures • Callable bonds • Single Step-Ups • Multi-Step Ups • Dual Currency – Equity and Commodity Linked Structures • Equity Linked Notes (ELNs) – coupon linked – principal linked • Commodity Linked Notes 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 11

Introduction to Structured Notes It is the presence of embedded derivatives, often options, that give structured notes their complexity. These difficult to understand difficult to value instruments make structured notes beyond the ability of many investors to fully understand. We need to look at these derivative components before proceeding to an examination of how structured notes are constructed. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 13

Introduction to Structured Notes What is an option? Options represent the right, but not the obligation, to buy some asset or to sell some asset at a fixed price for a limited period of time. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 14

Introduction to Structured Notes Calls and Puts: Options fall into two basic groups, calls and puts. Each represents a class of options. Call options: Call options, or more simply calls, give their owner (holder) the right but not the obligation to buy a specific quantity of some asset from the option writer for a set period of time at a fixed price. The asset is called the underlying asset, the set period of time is called the time to expiration or time to expiry, and the fixed price is called the strike price or exercise price. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 15

Introduction to Structured Notes Put options: Put options, or more simply puts, give their owner (holder) the right but not the obligation to sell a specific quantity of some asset to the option writer for a set period of time at a fixed price. The asset is called the underlying asset, the set period of time is called the time to expiration or time to expiry, and the fixed price is called the strike price or exercise price. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 16

Introduction to Structured Notes Premiums: At the time of purchase, the option buyer pays the option writer a sum of money for the right that the option conveys. This sum represents the price paid for the option and it is called the option premium. After paying the option premium, the long has no further obligations. Premium = intrinsic value + time value 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 17

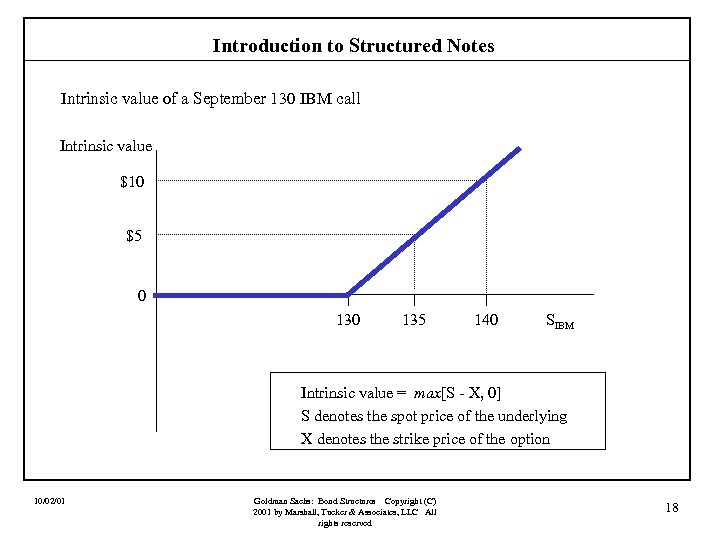Introduction to Structured Notes Intrinsic value of a September 130 IBM call Intrinsic value $10 $5 0 135 140 SIBM Intrinsic value = max[S - X, 0] S denotes the spot price of the underlying X denotes the strike price of the option 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 18

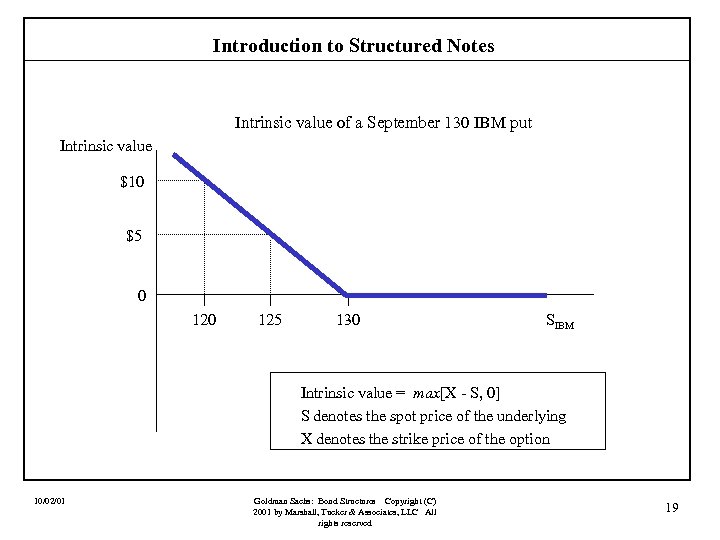Introduction to Structured Notes Intrinsic value of a September 130 IBM put Intrinsic value $10 $5 0 125 130 SIBM Intrinsic value = max[X - S, 0] S denotes the spot price of the underlying X denotes the strike price of the option 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 19

Introduction to Structured Notes Multi-Period Options: Multi-period options were first introduced in the mid 1980 s (around 1986). They came about because the swaps desks 1 recognized a new variation of the put/call parity theorem. It turns out that a long position in an interest rate swap is equivalent to a portfolio consisting of a long position in a multi-period call option on an interest rate and a short position in a multi-period put option on an interest rate. Since most interest rates swaps were written on 6 -month LIBOR 2, the implied multiperiod options are options on LIBOR. -------------1 2 10/02/01 Swaps desks later became known as derivatives desks or DPGs. This was especially true in the mid 1980 s. Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 21

Introduction to Structured Notes The multi-period calls on interest rates were first sold to corporations that had issued floating rate notes that paid LIBOR. When LIBOR went down, these corporations’ funding costs were reduced. But, when LIBOR went up, these corporations’ funding costs increased. The options allowed the corporations to place an upper limit on their funding costs. That is, they place a “ceiling” or “cap” their interest cost. As a result, these options became known as interest rate caps. The opposite of a ceiling (cap) is a floor, so the multi-period puts became known as interest rate floors. The life of a multi-period option is called its tenor. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 22

Introduction to Structured Notes payoff Call today 0. 5 expiration Time (years) payoff today payoff 0. 5 1. 0 1. 5 settlement Cap settlement Payoff = max[L - 7%, 0] NP Actual/360 S 10/02/01 X Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved LIBOR is quoted on an annual basis 23

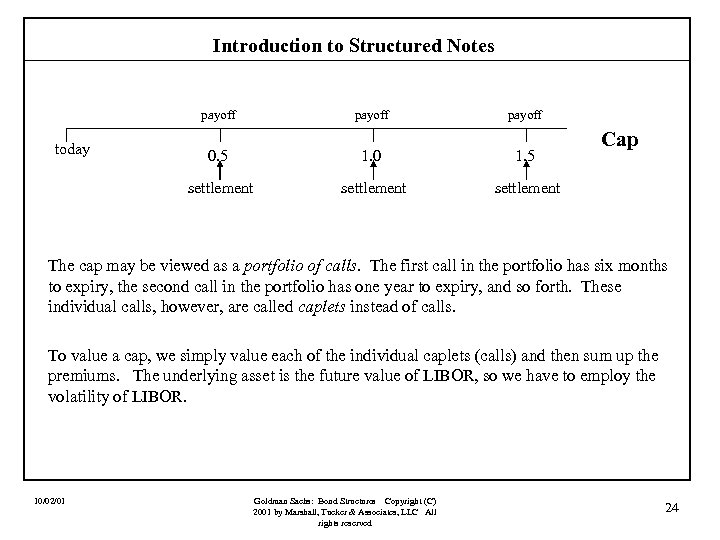Introduction to Structured Notes payoff today payoff 0. 5 1. 0 1. 5 settlement Cap settlement The cap may be viewed as a portfolio of calls. The first call in the portfolio has six months to expiry, the second call in the portfolio has one year to expiry, and so forth. These individual calls, however, are called caplets instead of calls. To value a cap, we simply value each of the individual caplets (calls) and then sum up the premiums. The underlying asset is the future value of LIBOR, so we have to employ the volatility of LIBOR. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 24

Introduction to Structured Notes Digital options: Digital options are options that can take on only one of two values. These are the values 1 and 0. They are also called binary options. Digital call or cap: max[ST – X, 0] Payoff = —————— ST – X Digital put or floor: max[X – ST, 0] Payoff = —————— X – ST 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 25

Introduction to Structured Notes All-or-nothing options (Ao. N): All-or-nothing options are a form of digital option. They are created by multiplying the value of a digital option by the spot price at expiry of some asset. Usually this is the underlying asset’s spot price, but it can be the price of some other asset or the spot price of the asset plus some sum. All-or-nothing call or cap: max[ST – X, 0] Payoff = ——————— (ST + Z) ST – X All-or-nothing put or floor: max[X – ST, 0] Payoff = ——————— (ST + Z) X – ST 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 26

Introduction to Structured Notes Collars: A involves a long position in the underlying coupled with a short call option and a long put option on that underlying. The strike of the call XC will be higher than the strike of the put XP. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 27

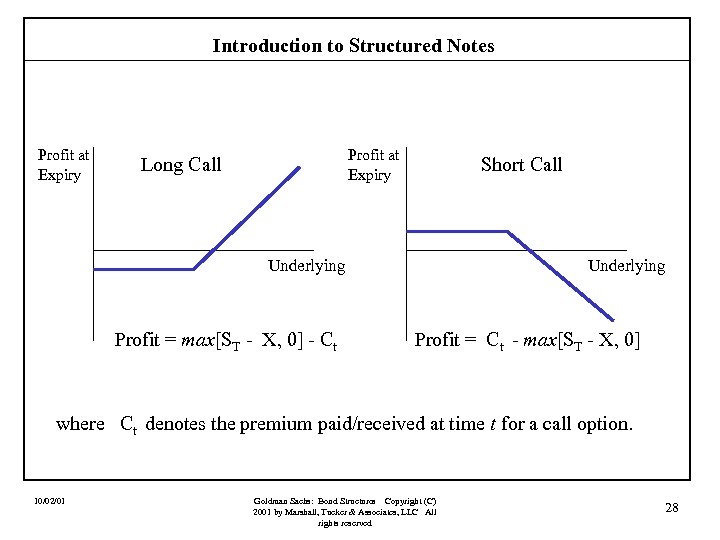Introduction to Structured Notes Profit at Expiry Long Call Short Call Underlying Profit = max[ST - X, 0] - Ct Underlying Profit = Ct - max[ST - X, 0] where Ct denotes the premium paid/received at time t for a call option. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 28

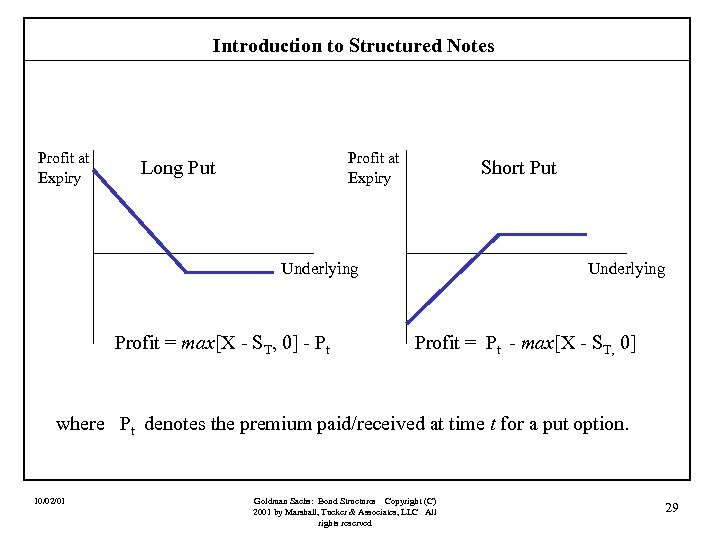Introduction to Structured Notes Profit at Expiry Long Put Short Put Underlying Profit = max[X - ST, 0] - Pt Underlying Profit = Pt - max[X - ST, 0] where Pt denotes the premium paid/received at time t for a put option. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 29

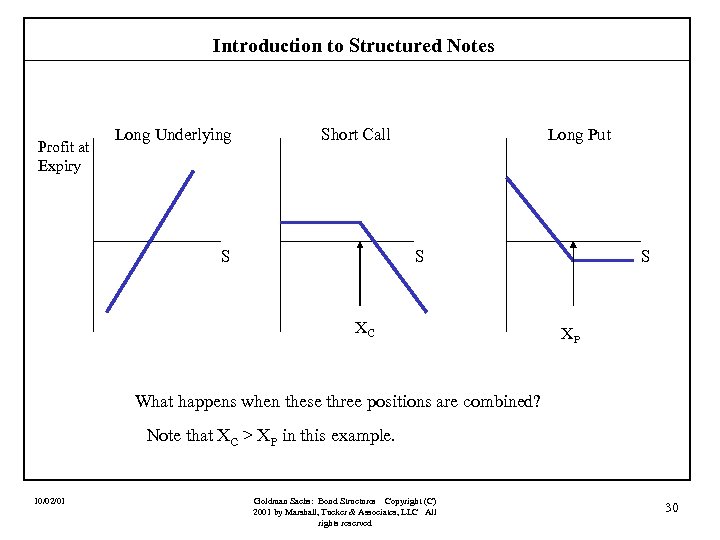Introduction to Structured Notes Profit at Expiry Long Underlying Short Call S Long Put S XC S XP What happens when these three positions are combined? Note that XC > XP in this example. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 30

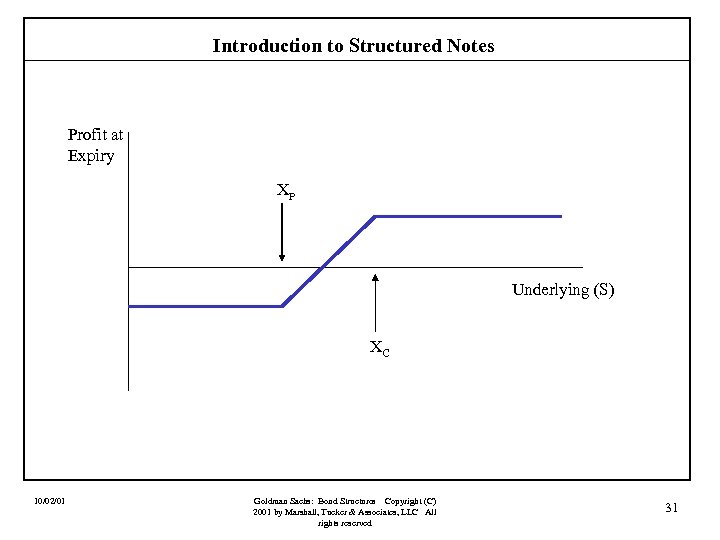Introduction to Structured Notes Forward Contracts: Originally, forward contracts were privately negotiated contracts for the delivery at a later date of some specific quantity of some specific asset. They were similar to futures contracts, but were not standardized and traded OTC. Over the past fifteen years, a new type of forward contract has evolved. These are cash settled based on the value of the underlying at a later date. Such forward contracts exist on interest rates (called forward rate agreements), on exchange rates (called forward exchange agreements), on commodities and on stocks. Unlike options, no up-front premium is paid or received to enter into a forward contract. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 32

Introduction to Structured Notes When written on stocks, forwards can be written on single stocks, on baskets of stocks, or on stock indexes. They are usually cash settled and the payment may be based on either capital appreciation alone or on the total return (including both capital appreciation and any dividend component). The total return is usually stated as a percentage (not annualized) and paid on some quantity of notional principal: Payoff = D × (TR - CR) × NP Where: 10/02/01 D is a dummy variable (+1 if long, -1 if short) TR is the total return over the relevant period CR is the contract rate set at the outset (analogous to a strike price) NP is the notional principal Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 33

Introduction to Structured Notes Example: Suppose that you bought a six-month forward contract on the total return on the S&P. The contract covers $50 million of notional principal. The contract rate is 6. 20% Payoff = D × (TRSP - CR) × NP = +1 × (TRSP - 6. 20%) × $50 million How does this payoff function differ from that of an option? Note: total return is generally stated on a “periodic basis” not on an annual basis the way interest rates are routinely stated. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 34

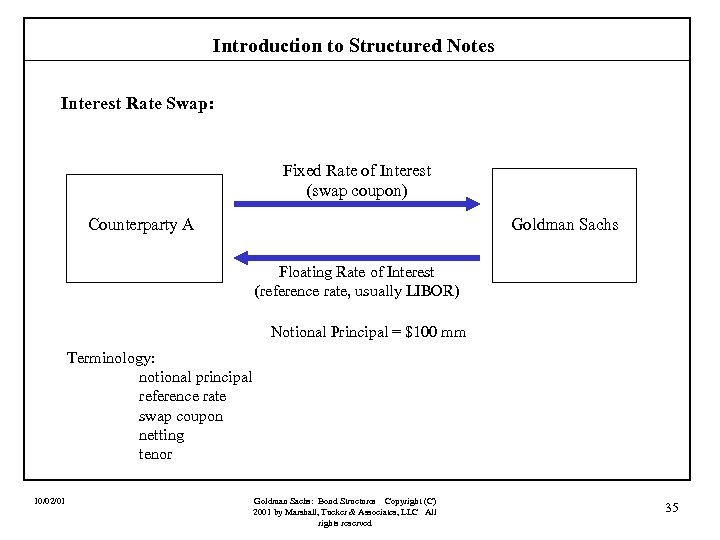Introduction to Structured Notes Interest Rate Swap: Fixed Rate of Interest (swap coupon) Counterparty A Goldman Sachs Floating Rate of Interest (reference rate, usually LIBOR) Notional Principal = $100 mm Terminology: notional principal reference rate swap coupon netting tenor 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 35

Introduction to Structured Notes Offer Bid 6. 72% 6. 68% Counterparty A Goldman Sachs DPG LIBOR Counterparty B LIBOR Notional Principal = $50 mm payments made semiannually tenor = 3 years 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 36

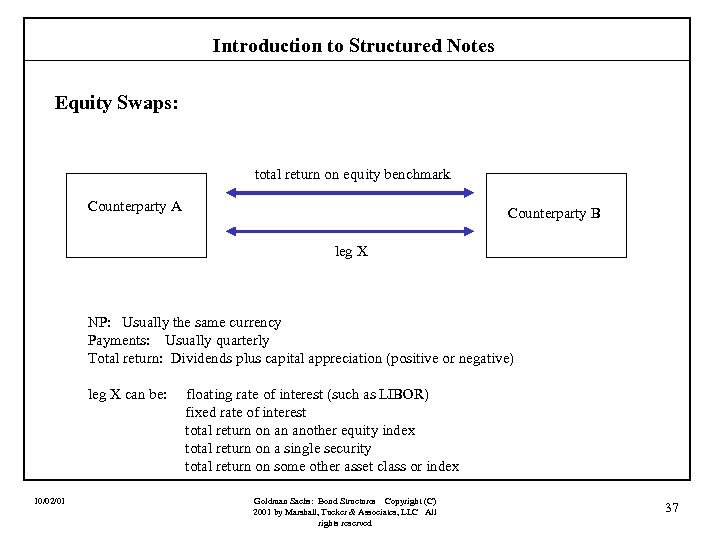Introduction to Structured Notes Equity Swaps: total return on equity benchmark Counterparty A Counterparty B leg X NP: Usually the same currency Payments: Usually quarterly Total return: Dividends plus capital appreciation (positive or negative) leg X can be: 10/02/01 floating rate of interest (such as LIBOR) fixed rate of interest total return on an another equity index total return on a single security total return on some other asset class or index Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 37

Early Structured Securities Callable Bonds Putable Bonds Convertible Bonds Commodity-Linked Bonds (civil war) 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 38

Introduction to Structured Notes We will assume in each example that the issuer wants to pay a fixed rate. But, in each case, the investor has a different need. Then, using the basic building blocks we will “engineer” the desired security. Note: In all the examples we will look at, we will ignore the difference between yields quoted on a bond basis and yields quoted on a money market basis. 1 We will also assume, unless stated otherwise, that payments will be made semiannually, so references to LIBOR imply 6 -M LIBOR. 1 Yields and coupons on bonds and coupons on swaps are quoted on a bond basis and LIBOR is quoted on a money market basis). 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 40

Introduction to Structured Notes Case I: A Straight Floater Assume that a corporation could issue a four year-fixed rate note if it agreed to pay a fixed rate of 8. 00%. An investor is willing to hold this corporation’s debt, but wants to receive a floating rate pegged to LIBOR. After some discussions with Goldman Sachs, it is understood that the investor will take the floater if the floater pays LIBOR + 130 bps. Let’s build it. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 41

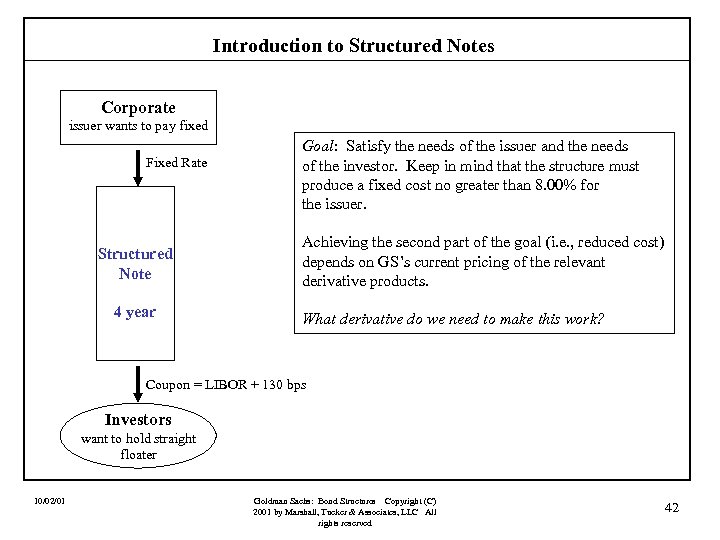Introduction to Structured Notes Corporate issuer wants to pay fixed Fixed Rate Structured Note 4 year Goal: Satisfy the needs of the issuer and the needs of the investor. Keep in mind that the structure must produce a fixed cost no greater than 8. 00% for the issuer. Achieving the second part of the goal (i. e. , reduced cost) depends on GS’s current pricing of the relevant derivative products. What derivative do we need to make this work? Coupon = LIBOR + 130 bps Investors want to hold straight floater 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 42

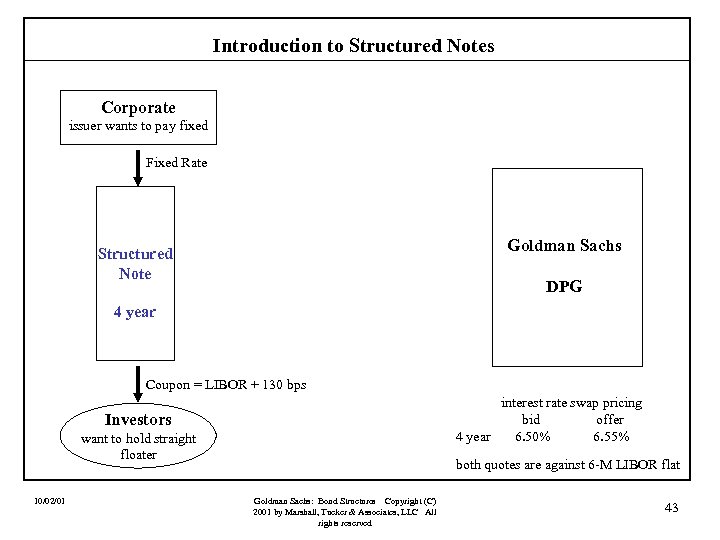Introduction to Structured Notes Corporate issuer wants to pay fixed Fixed Rate Goldman Sachs Structured Note DPG 4 year Coupon = LIBOR + 130 bps interest rate swap pricing bid offer 4 year 6. 50% 6. 55% Investors want to hold straight floater 10/02/01 both quotes are against 6 -M LIBOR flat Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 43

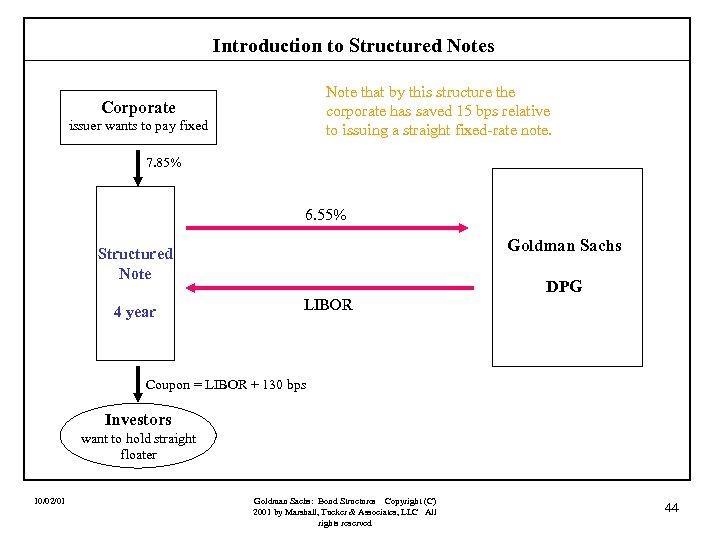Introduction to Structured Notes Note that by this structure the corporate has saved 15 bps relative to issuing a straight fixed-rate note. Corporate issuer wants to pay fixed 7. 85% 6. 55% Goldman Sachs Structured Note 4 year DPG LIBOR Coupon = LIBOR + 130 bps Investors want to hold straight floater 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 44

Introduction to Structured Notes Case II: A Capped Floater Assume that a corporation could issue a four-year fixed rate note if it agreed to pay a fixed rate of 8. 00%. An investor is willing to hold this corporation’s debt, but wants to receive a floating rate pegged to LIBOR and is willing to accept a cap of 9% (i. e. , under no circumstances with the coupon exceed 9%). After some discussions with Goldman Sachs, it is understood that the investor will take the floater if the floater pays LIBOR + 150 bps. Let’s build it. Note, that this investor wants 20 bps more than the prior investor. Why? 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 45

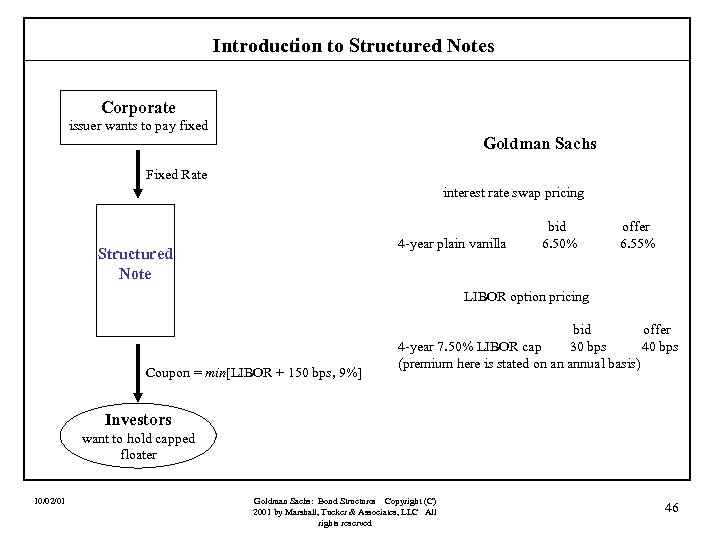Introduction to Structured Notes Corporate issuer wants to pay fixed Goldman Sachs Fixed Rate interest rate swap pricing 4 -year plain vanilla Structured Note bid 6. 50% offer 6. 55% LIBOR option pricing Coupon = min[LIBOR + 150 bps, 9%] bid offer 4 -year 7. 50% LIBOR cap 30 bps 40 bps (premium here is stated on an annual basis) Investors want to hold capped floater 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 46

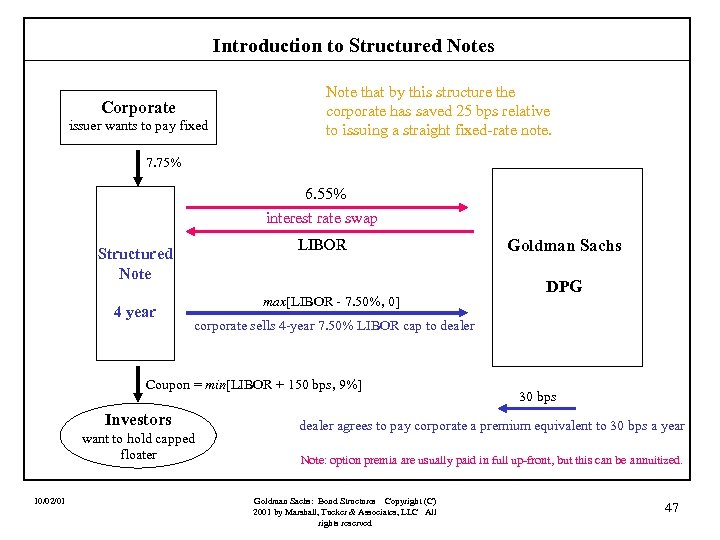Introduction to Structured Notes Corporate issuer wants to pay fixed Note that by this structure the corporate has saved 25 bps relative to issuing a straight fixed-rate note. 7. 75% 6. 55% interest rate swap LIBOR Structured Note 4 year max[LIBOR - 7. 50%, 0] DPG corporate sells 4 -year 7. 50% LIBOR cap to dealer Coupon = min[LIBOR + 150 bps, 9%] Investors want to hold capped floater 10/02/01 Goldman Sachs 30 bps dealer agrees to pay corporate a premium equivalent to 30 bps a year Note: option premia are usually paid in full up-front, but this can be annuitized. Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 47

Introduction to Structured Notes Case III: A Collared Floater Assume that a corporation could issue a four-year fixed rate note if it agreed to pay a fixed rate of 8. 00%. An investor is willing to hold this corporation’s debt, but wants to receive a floating rate pegged to LIBOR and is willing to accept a cap of 9% provided that the note will also have a floor of 6% (i. e. , under no circumstances will the coupon exceed 9% or be less than 6%). After some discussions with Goldman Sachs, it is understood that the investor will take the floater if the floater pays LIBOR + 100 bps. Let’s build it. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 48

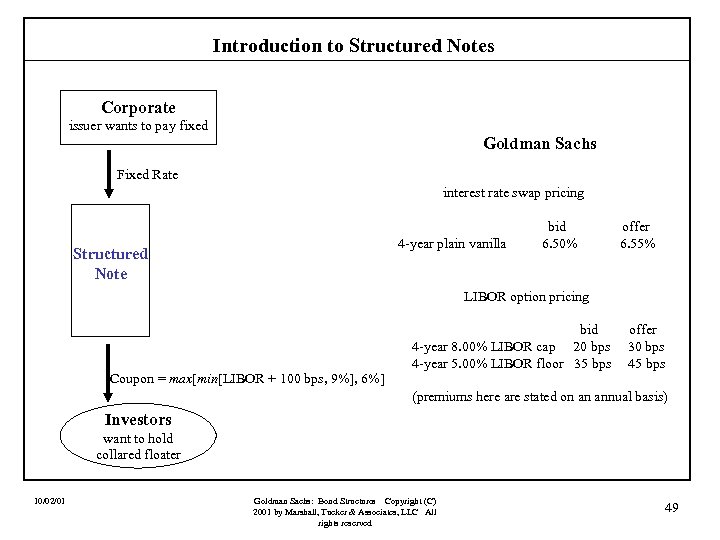Introduction to Structured Notes Corporate issuer wants to pay fixed Goldman Sachs Fixed Rate interest rate swap pricing 4 -year plain vanilla Structured Note bid 6. 50% offer 6. 55% LIBOR option pricing bid 4 -year 8. 00% LIBOR cap 20 bps 4 -year 5. 00% LIBOR floor 35 bps offer 30 bps 45 bps Coupon = max[min[LIBOR + 100 bps, 9%], 6%] (premiums here are stated on an annual basis) Investors want to hold collared floater 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 49

Introduction to Structured Notes Corporate issuer wants to pay fixed 7. 80% Note that by this structure the corporate has saved 20 bps relative to issuing a straight fixed-rate note. 6. 55% interest rate swap LIBOR Structured Note max[LIBOR - 8. 00%, 0] corporate sells 4 -year 8. 00% LIBOR cap to dealer (dealer agrees to pay corporate 20 bps a year) max[5. 00% - LIBOR, 0] 4 year Goldman Sachs DPG corporate buys 4 -year 5. 00% LIBOR floor from dealer (corporate agrees to pay dealer 45 bps a year) Coupon = max[min[LIBOR + 100 bps, 9%], 6%] 20 bps Investors want to hold collared floater 10/02/01 45 bps Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 50

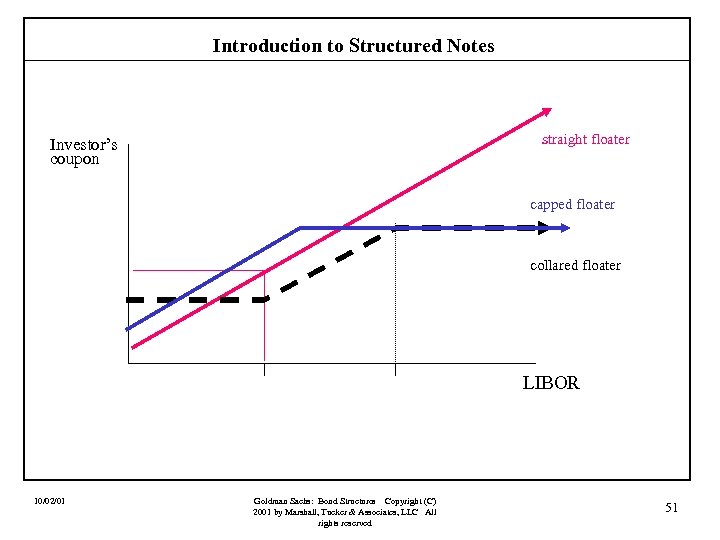Introduction to Structured Notes straight floater Investor’s coupon capped floater collared floater LIBOR 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 51

Introduction to Structured Notes The issuance of structured securities, often through private placements, allows the issuer to tap into different demand segments (i. e. , straight floaters, capped floaters, collared floaters, etc. ). By tailoring different portions of the issuance to specific investor demands, Goldman Sachs is often able to help the issuer to reduce its financing costs relative to a straight issuance of its desired type of liability. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 52

Introduction to Structured Notes Before moving on to equity and commodity linked notes, we look at two more types of floating rate structured notes: Range floaters (also called range notes) CMT floaters 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 53

Introduction to Structured Notes Case IV: A Range Floater (also called a range note) Assume that a corporation could issue a four-year fixed rate note if it agreed to pay a fixed rate of 8. 00%. An investor is willing to hold this corporation’s debt, but wants to receive a floating rate pegged to LIBOR provided that LIBOR stays within a very well defined range of 5% to 8%. The investor feels very confident that LIBOR will stay within the range. The investor is willing to hold the range floater provided it pays LIBOR + 200 bps while LIBOR is within the range and the investor is willing to accept nothing if LIBOR strays outside the range. This structure requires all-or-nothing options! Let’s build it. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 54

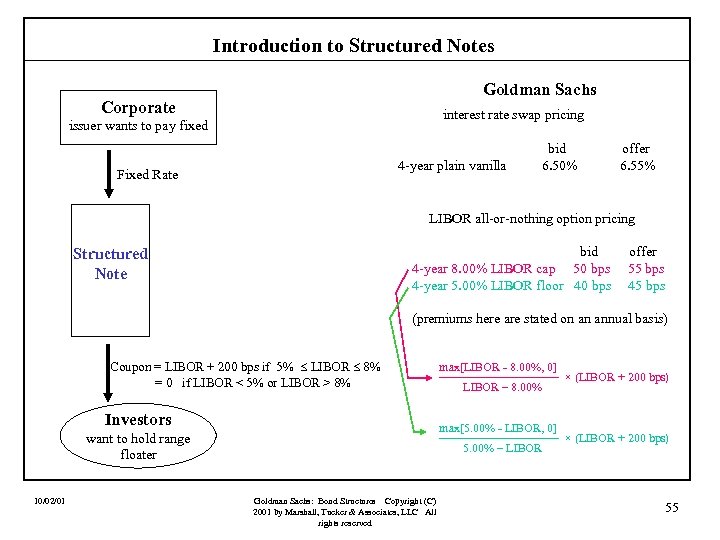Introduction to Structured Notes Goldman Sachs Corporate interest rate swap pricing issuer wants to pay fixed 4 -year plain vanilla Fixed Rate bid 6. 50% offer 6. 55% LIBOR all-or-nothing option pricing bid 4 -year 8. 00% LIBOR cap 50 bps 4 -year 5. 00% LIBOR floor 40 bps Structured Note offer 55 bps 45 bps (premiums here are stated on an annual basis) Coupon = LIBOR + 200 bps if 5% LIBOR 8% = 0 if LIBOR < 5% or LIBOR > 8% Investors max[5. 00% - LIBOR, 0] ————— × (LIBOR + 200 bps) 5. 00% – LIBOR want to hold range floater 10/02/01 max[LIBOR - 8. 00%, 0] ————— × (LIBOR + 200 bps) LIBOR – 8. 00% Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 55

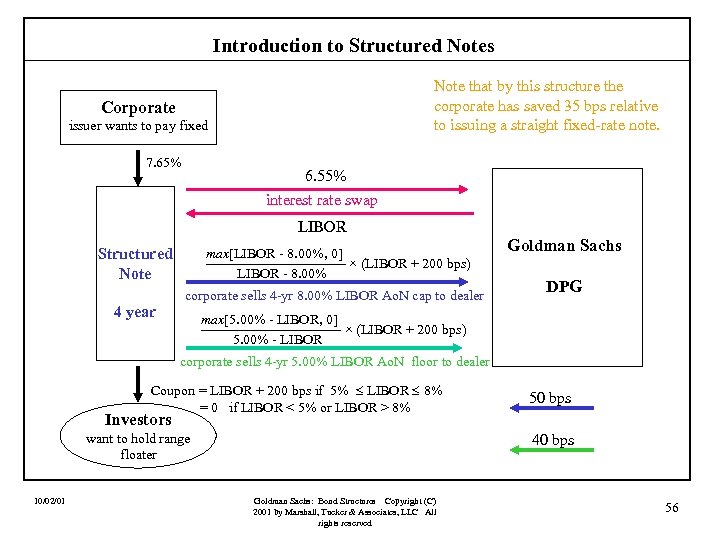Introduction to Structured Notes Note that by this structure the corporate has saved 35 bps relative to issuing a straight fixed-rate note. Corporate issuer wants to pay fixed 7. 65% 6. 55% interest rate swap LIBOR Structured Note 4 year max[LIBOR - 8. 00%, 0] ————— × (LIBOR + 200 bps) LIBOR - 8. 00% corporate sells 4 -yr 8. 00% LIBOR Ao. N cap to dealer Goldman Sachs DPG max[5. 00% - LIBOR, 0] ————— × (LIBOR + 200 bps) 5. 00% - LIBOR corporate sells 4 -yr 5. 00% LIBOR Ao. N floor to dealer Coupon = LIBOR + 200 bps if 5% LIBOR 8% = 0 if LIBOR < 5% or LIBOR > 8% 50 bps Investors want to hold range floater 10/02/01 40 bps Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 56

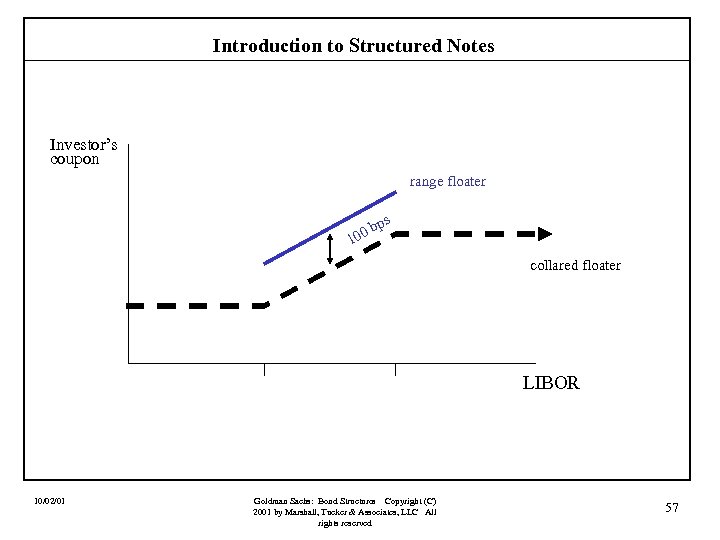Introduction to Structured Notes Investor’s coupon range floater ps b 100 collared floater LIBOR 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 57

Introduction to Structured Notes Case V: CMT Floater Assume that a corporation could issue a four-year fixed rate note if it agreed to pay a fixed rate of 8. 00%. An investor is willing to hold this corporation’s debt, but wants to receive a floating rate pegged to the yield on the 5 -year on-the-run Treasury. Specifically, the investor is willing to hold the debt if it pays the 5 -yr CMT plus 80 bps. This structure requires a CMT swap! Let’s build it. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 58

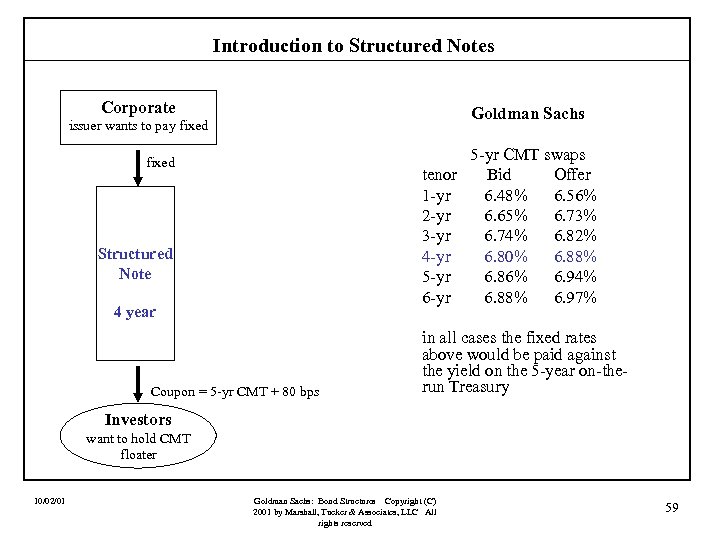Introduction to Structured Notes Corporate Goldman Sachs issuer wants to pay fixed 5 -yr CMT swaps tenor Bid Offer 1 -yr 6. 48% 6. 56% 2 -yr 6. 65% 6. 73% 3 -yr 6. 74% 6. 82% 4 -yr 6. 80% 6. 88% 5 -yr 6. 86% 6. 94% 6 -yr 6. 88% 6. 97% fixed Structured Note 4 year Coupon = 5 -yr CMT + 80 bps in all cases the fixed rates above would be paid against the yield on the 5 -year on-therun Treasury Investors want to hold CMT floater 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 59

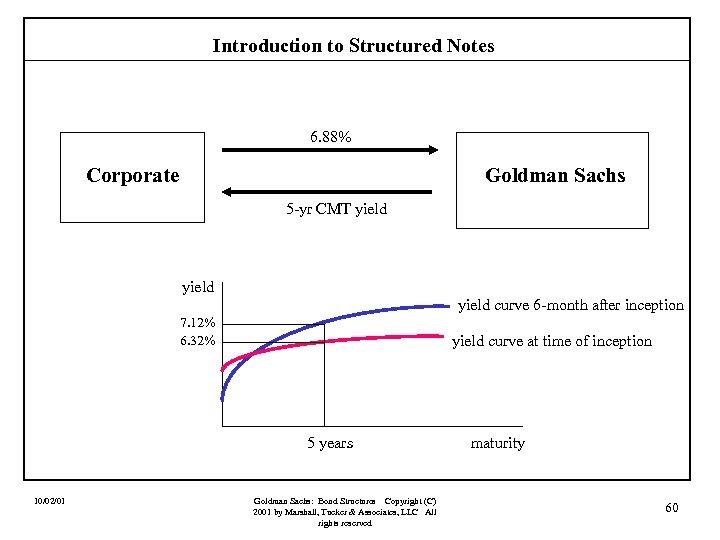Introduction to Structured Notes 6. 88% Corporate Goldman Sachs 5 -yr CMT yield curve 6 -month after inception 7. 12% 6. 32% yield curve at time of inception 5 years 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved maturity 60

Introduction to Structured Notes Note that by this structure the corporate has saved 32 bps relative to issuing a straight fixed-rate note. Corporate issuer wants to pay fixed 7. 68% 6. 88% Structured Note 4 year Goldman Sachs CMT interest rate swap DPG yield on 5 -yr CMT Coupon = 5 -yr CMT + 80 bps Investors want to hold CMT floater 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 61

Introduction to Structured Notes There are many types of fixed rate structured notes. Some employ a fixed coupon that periodically “steps up” or “steps down” to preset higher or lower levels. These are created using step up and step down interest rate swaps. Others pay a fixed rate in a currency other than that in which the note is denominated. We will look at this latter structure. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 63

Introduction to Structured Notes Case VI: Dual Currency Fixed Rate Structure Assume that a corporation could issue a four-year fixed rate note if it agreed to pay a fixed rate of 8. 00%. An investor is willing to hold this corporation’s debt, but wants to receive a fixed rate in euros rather than in dollars, because the investor feels that the euro will strengthen against the dollar over the next few years. But, the investor wants the bond to be redeemed at maturity for dollars (that is, the par value will be returned at maturity in dollars). The investor requires a fixed rate of 8. 10% on the euro par value equivalent (at the time the swap is written). 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 64

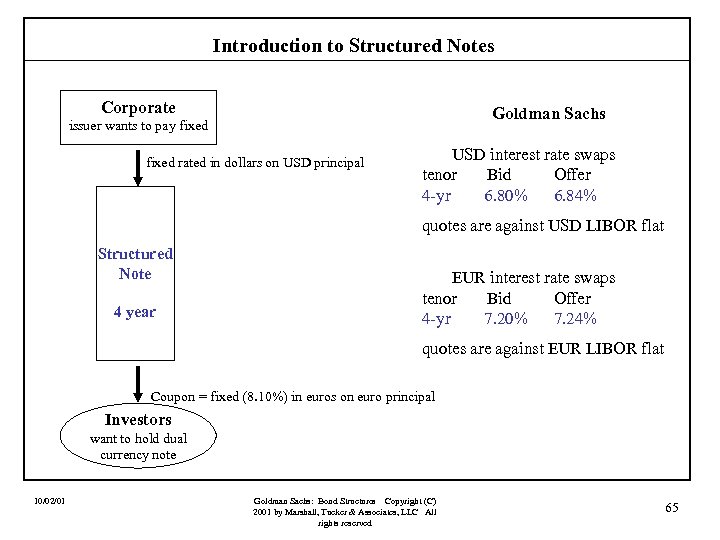Introduction to Structured Notes Corporate Goldman Sachs issuer wants to pay fixed rated in dollars on USD principal USD interest rate swaps tenor Bid Offer 4 -yr 6. 80% 6. 84% quotes are against USD LIBOR flat Structured Note 4 year EUR interest rate swaps tenor Bid Offer 4 -yr 7. 20% 7. 24% quotes are against EUR LIBOR flat Coupon = fixed (8. 10%) in euros on euro principal Investors want to hold dual currency note 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 65

Introduction to Structured Notes Assume spot exchange rate is 1 euro = $0. 90 6. 84% on USD Corporate Goldman Sachs USD IR Swap Goldman Sachs IR Parity Goldman Sachs EUR IR Swap USD LIBOR Corporate EUR LIBOR Corporate 7. 20% on EUR 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 66

Introduction to Structured Notes 6. 84% on USD + 86 bps Corporate Goldman Sachs USD IR Swap Goldman Sachs IR Parity Goldman Sachs EUR IR Swap USD LIBOR + 86 bps Corporate EUR LIBOR + 90 bps Corporate 7. 20% on EUR +90 bps Begin here 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 67

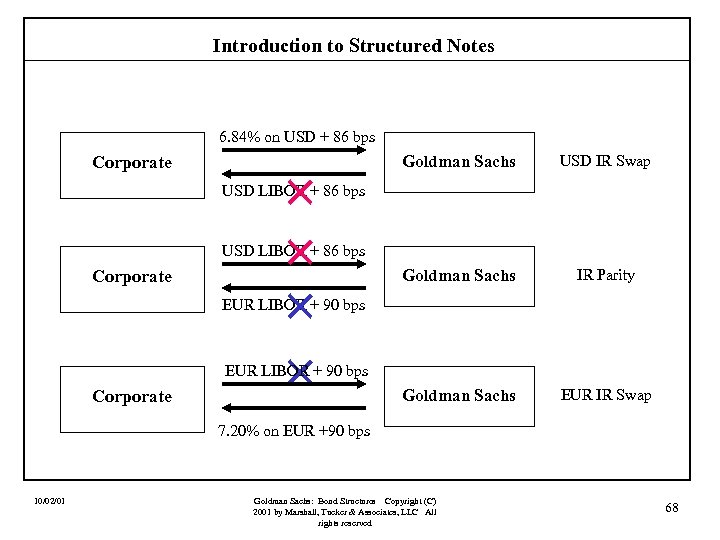Introduction to Structured Notes 6. 84% on USD + 86 bps Corporate × × Goldman Sachs USD IR Swap Goldman Sachs IR Parity Goldman Sachs EUR IR Swap USD LIBOR + 86 bps Corporate EUR LIBOR + 90 bps Corporate 7. 20% on EUR +90 bps 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 68

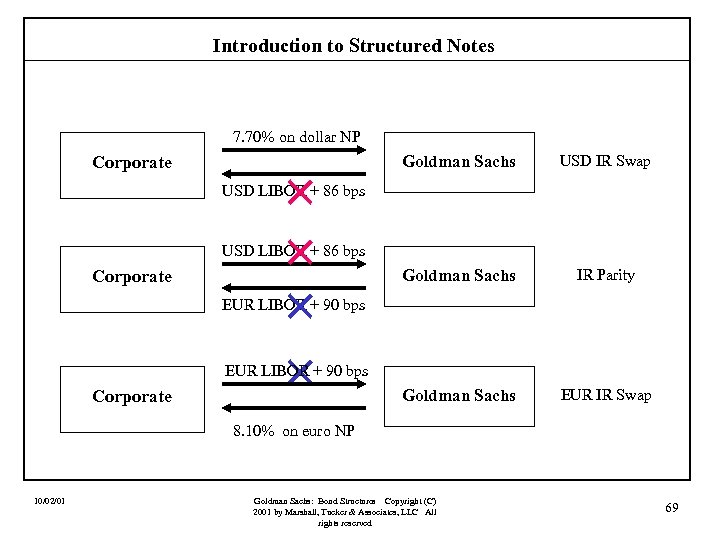Introduction to Structured Notes 7. 70% on dollar NP Corporate × × Goldman Sachs USD IR Swap Goldman Sachs IR Parity Goldman Sachs EUR IR Swap USD LIBOR + 86 bps Corporate EUR LIBOR + 90 bps Corporate 8. 10% on euro NP 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 69

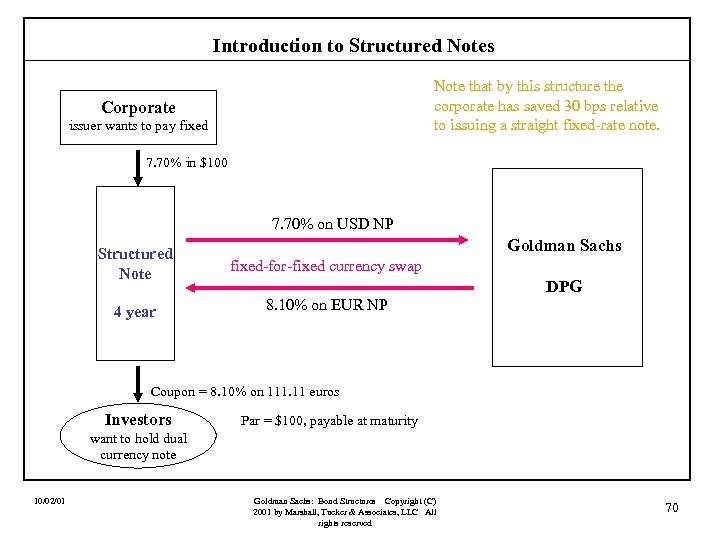Introduction to Structured Notes Note that by this structure the corporate has saved 30 bps relative to issuing a straight fixed-rate note. Corporate issuer wants to pay fixed 7. 70% in $100 7. 70% on USD NP Goldman Sachs Structured Note fixed-for-fixed currency swap 4 year 8. 10% on EUR NP DPG Coupon = 8. 10% on 111. 11 euros Investors Par = $100, payable at maturity want to hold dual currency note 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 70

Introduction to Structured Notes Equity Linked Notes: Equity linked notes are debt instruments that pay a coupon that is linked to the return on some equity index or some equity basket. Alternatively, the coupon could be fixed, but the principal at maturity might be linked to some equity index or basket. We will consider the construction of both types. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 72

Introduction to Structured Notes Case VII: An Equity-Linked Coupon Structure (principal protected). Assume that a corporation could issue a four-year fixed rate note if it agreed to pay a fixed rate of 8. 00% in two semiannual installments. An investor is willing to hold this corporation’s debt, but wants to receive a coupon tied to the performance of some equity index. At the same time, the investor wants the principal on the note protected so that he is assured of full repayment at maturity. Finally, it is important that the coupon never be negative! Suppose that the investor would be willing to take a coupon tied to the total return on the S&P 500 (TRSP) and that payments will be made quarterly. Specifically, the note would pay max[TRSP - 100 bps, 0] quarterly. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 73

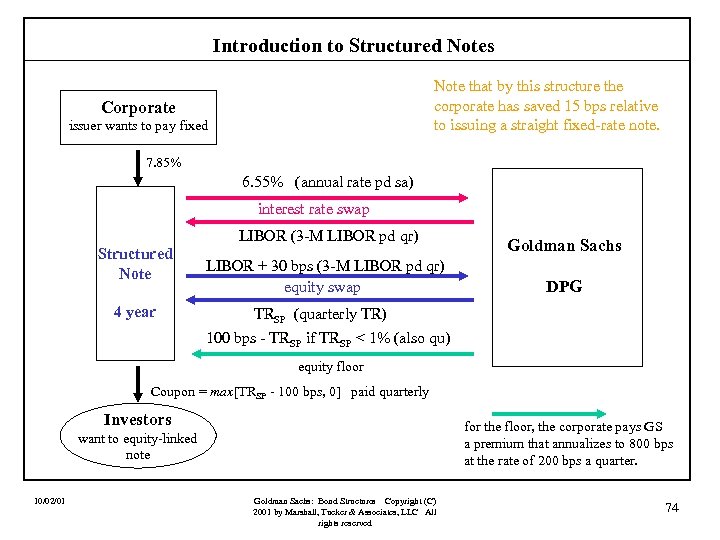Introduction to Structured Notes Note that by this structure the corporate has saved 15 bps relative to issuing a straight fixed-rate note. Corporate issuer wants to pay fixed 7. 85% 6. 55% (annual rate pd sa) interest rate swap LIBOR (3 -M LIBOR pd qr) Structured Note 4 year LIBOR + 30 bps (3 -M LIBOR pd qr) equity swap Goldman Sachs DPG TRSP (quarterly TR) 100 bps - TRSP if TRSP < 1% (also qu) equity floor Coupon = max[TRSP - 100 bps, 0] paid quarterly Investors for the floor, the corporate pays GS a premium that annualizes to 800 bps at the rate of 200 bps a quarter. want to equity-linked note 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 74

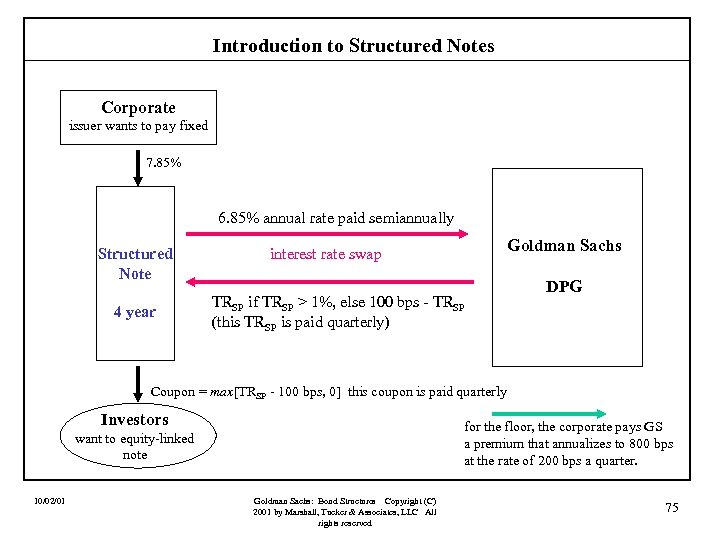Introduction to Structured Notes Corporate issuer wants to pay fixed 7. 85% 6. 85% annual rate paid semiannually Structured Note 4 year Goldman Sachs interest rate swap TRSP if TRSP > 1%, else 100 bps - TRSP (this TRSP is paid quarterly) DPG Coupon = max[TRSP - 100 bps, 0] this coupon is paid quarterly Investors for the floor, the corporate pays GS a premium that annualizes to 800 bps at the rate of 200 bps a quarter. want to equity-linked note 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 75

Introduction to Structured Notes Case VIII: An Equity-Linked Principal Structure (principal protected). Assume that a corporation could issue a four-year fixed rate note if it agreed to pay a fixed rate of 8. 00% in two semiannual installments. An investor is willing to hold this corporation’s debt. The investor wants to receive a fixed coupon and would accept 3. 00%, provided that the investor would also receive that portion of the 4 -year total return on the S&P 500 in excess of 48%, provided that is a positive sum. Suppose that Goldman Sachs would sell a four-year call option whose payout is as follows: Payout at end of four years = max[TRSP - 48%, 0] GS would charge 450 bps a year in semiannual installments of 225 bps each. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 76

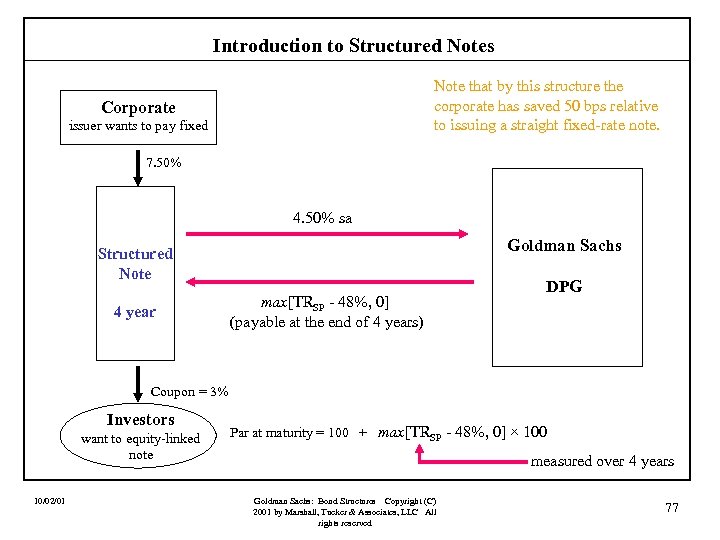Introduction to Structured Notes Note that by this structure the corporate has saved 50 bps relative to issuing a straight fixed-rate note. Corporate issuer wants to pay fixed 7. 50% 4. 50% sa Goldman Sachs Structured Note 4 year max[TRSP - 48%, 0] (payable at the end of 4 years) DPG Coupon = 3% Investors want to equity-linked note 10/02/01 Par at maturity = 100 + max[TRSP - 48%, 0] × 100 measured over 4 years Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 77

Introduction to Structured Notes Case Study I: Goldman Sachs-Skopbank • • 10/02/01 December 1989 Japanese life insurance companies seeking enhanced interest income Skopbank AAA rated Skopbank traditional funding in US dollars and at $LIBOR flat Nikkei 225 at about 38, 200 Seasoned 1 -year AAA-rated Euro-Yen bonds yielding 6. 10% Yen-dollar rate at about Y 144/US$1 Annualized vol of Nikkei about 13% (in Yen) Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 79

Introduction to Structured Notes • Terms of Issuance: Issuer: Size: Coupon: Maturity: Issue Price: Call Options: Denomination: Commissions: Redemption: Skopbank Y 6. 7 billion 7% 1 Year 101 -1/8 None Y 100 million 1 -1/8 If at maturity, Nikkei > 31, 870. 04, then redemption at par. If Nikkei < 23, 902. 53, then redemption is zero. If in between, then redemption is Y 100 million x {1 - [(4)(31, 870. 04 - Nikkei)/(31, 870. 04)]} 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 80

Introduction to Structured Notes • Skopbank issues a plain-vanilla 1 -year, fixed-rate Euro-Yen bond and buys an embedded, European-style, out-of-the-money capped put on the Nikkei 225. • A capped put is a combination of two puts, short one put with a higher exercise price and long an otherwise identical put with a lower exercise price. Here the two strike prices are 31, 870. 04 and 23, 902. 53. The capped put precludes the investor (Japanese life insurance companies) from having to pay the issuer (negative redemption) should the Nikkei fall below 23, 902. 53 at expiration. The capped put is out-of-the-money because the two strikes are well below the current level of the Nikkei at issuance (38, 200). • The instrument is coupon guaranteed by not principal guaranteed. The principal component has four times leverage. • The investor picks up 90 basis points in enhanced coupon for writing the capped put. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 81

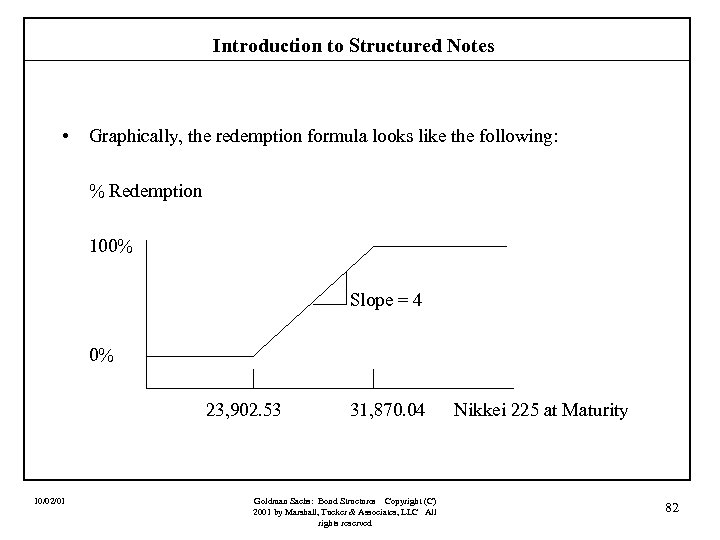Introduction to Structured Notes • Graphically, the redemption formula looks like the following: % Redemption 100% Slope = 4 0% 23, 902. 53 10/02/01 31, 870. 04 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved Nikkei 225 at Maturity 82

Introduction to Structured Notes • Skopbank will seek to “reverse engineer” the issue and, economically speaking, get back to floating dollar funding at sub-LIBOR. Skopbank will need to achieve a sub-LIBOR funding rate because (a) otherwise it would just issue floating dollar funding in the first place, and (b) it will assume some counter party credit risk with Goldman. • Specifically, Skopbank will look to sell off its embedded capped put to Goldman (enter Goldman’s equity derivatives desk) and to convert the Yendenominated fixed coupon obligation to a floating dollar obligation (enter Goldman’s cross-currency interest rate swap desk). Skopbank will convert the Yen proceeds from the issue into dollars, and reconvert dollars back to Yen via the real principals on the swap. • Note that I do not have the exact terms of the swap done in this deal, so the figures appearing on the next page are just representative. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 83

Introduction to Structured Notes • We have: Skopbank Capped Put on Nikkei 1 -1/8% Commission (or about $525, 000) Yen 6. 7 billion (today) 100% + $LIBOR - 20 bps (in one year on $46. 5278 million) Goldman Sachs $46. 5278 million (today) 107% (in one year on Yen 6. 7 billion) 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 84

Introduction to Structured Notes • In this case, at the end of the day, Skopbank has issued about $46. 5278 million at an all-in cost of 20 basis points below $LIBOR. • How much money Goldman makes all-in depends critically on what it will fetch for the capped put. (In addition, Goldman will have to hedge the risks occasioned by the cross-currency interest rate swap transaction. ) In this case, Goldman refashioned the Nikkei puts and resold them to retail investors as Nikkei Put Warrants listed on the Amex. (One might say that Goldman could profit if the implied vol of the embedded put was lower than that of the listed put it in turn sold. ) • On a forensic note, the Nikkei closed at around 23, 000 at the maturity of the Skopbank issue. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 85

Introduction to Structured Notes Case Study II: Goldman-Disney • • 10/02/01 In 1985, Disney acquired Arvida (real estate inventories) and paid greenmail to Saul Steinberg As a result, Disney had a substantially more levered balance sheet and had a significant debt maturity profile problem. It had $862 million in debt ($215 million to acquire Arvida and $328 million to repurchase 4. 2 million shares from Steinberg). TD/TA rose from to 43% from about 20% just one year earlier. Two-thirds of the total debt consisted of short-term bank loans and CP. Disney was rated a weak single A. Since 1983, Disney had a licensing agreement with a Japanese company related to Disney Tokyo. Gate receipts were rising and so were Disney’s Yendenominated royalties, but the dollar had been depreciating, occasioning losses on the exchange component. Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 86

Introduction to Structured Notes • Thus Disney’s treasury officers sought to solve both problems by, in part, issuing long-term debt in Yen, converting the proceeds to dollars and paying down some of the short-term bank loans and CP, and using the Yendenominated gate receipts to service the debt. • Being a weak single A, a Euro-yen issue by Disney could not float in the Eurobond marketplace. • Disney could obtain a 10 -year Yen term loan from a consortium of Japanese banks. The loan would be fixed rate with a s. a. coupon of 3. 75% and up front fees of 75 basis points. The principal would be Yen 15 billion or, at an exchange rate at the time of about Y 250/US$1, about $60 million. Thus the all -in cost of the loan, in Yen, would be 7. 75% p. a. (r = IRR = 3. 804% s. a. or 7. 75% p. a. ): 100. 00 - 0. 75 = 3. 75/(1 + r) + 3. 75/(1 + r)^2 + … + 103. 75/(1 + r)^20. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 87

Introduction to Structured Notes • Goldman suggested an alternative strategy to Disney whereby it would issue a 10 year Euro-ECU bond and then swap to Yen. The ECU proceeds would be exchanged in the spot market for dollars and used to pay down some of Disney’s short-term debt, thus restructuring its debt maturity profile. The Disney Tokyo Yen -denominated royalties would be used to service the swap payments. (The ECU was a trade-weighted basket of Common Market currencies and the forerunner of today’s euro. At the time, the ECU was the second leading European currency behind then West German mark. ) • Goldman had identified a AAA-rated French utility with an already outstanding Euro-Yen bond that had about 10 years to maturity and was yielding about 6. 83% p. a. It also had a 10 -year outstanding Euro-ECU bond that was yielding about 9. 37%. • So the question was, Could Disney issue Euro-ECU and swap to Yen at an all-in funding cost that was lower than the 7. 75% p. a. rate on the Japanese term loan? And could Goldman and the French utility profit too? 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 88

Introduction to Structured Notes • The terms of the Euro-ECU bond were: Par: ECU 80 million (also about $60 million at the time) Price: 100. 250% Coupon: 9. 125% p. a. Fees: 2% Expenses: $75, 000 Sinking Fund: 5 -year straight line beginning in Year 6 Dollar/ECU: $0. 7420 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 89

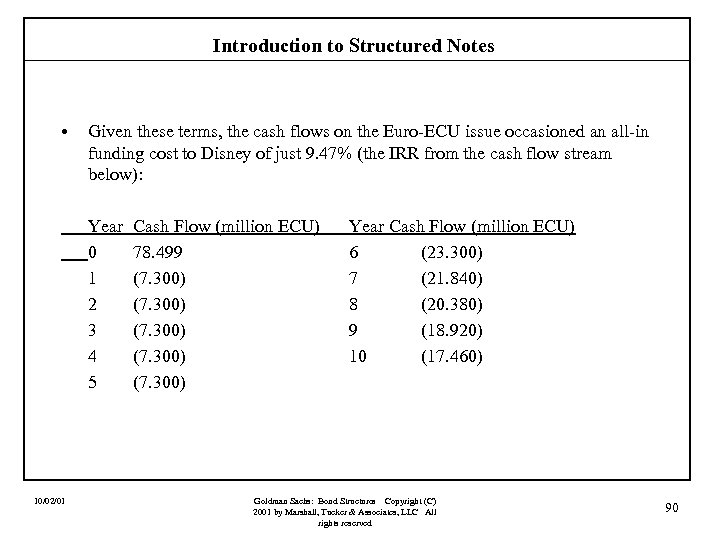Introduction to Structured Notes • Given these terms, the cash flows on the Euro-ECU issue occasioned an all-in funding cost to Disney of just 9. 47% (the IRR from the cash flow stream below): Year 0 1 2 3 4 5 10/02/01 Cash Flow (million ECU) 78. 499 (7. 300) Year Cash Flow (million ECU) 6 (23. 300) 7 (21. 840) 8 (20. 380) 9 (18. 920) 10 (17. 460) Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 90

Introduction to Structured Notes • At this point we can readily see an arbitrage opportunity. Call it “relative credit spread arbitrage”. As the table below indicates, whereas the French utility being rated AAA has an absolute advantage in issuing in both ECU and Yen, Disney has a comparative advantage in issuing in ECU. Disney’s relative credit spread in ECU is just 10 basis points, whereas it is 92 basis points in Yen. Buyers of the Euro-ECU issue appear to be overpricing the issue. The difference between the two relative credit spreads is 82 basis points and represents the “pie” that can be sliced up among Disney, the French utility, and a swap dealer (presumably Goldman at first thought). Fr. Utility (AAA) Disney (A-) Spread 10/02/01 ECU 9. 37% p. a. 9. 47% p. a. 10 bps Yen 6. 83% p. a. 7. 75% p. a. 92 bps Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 91

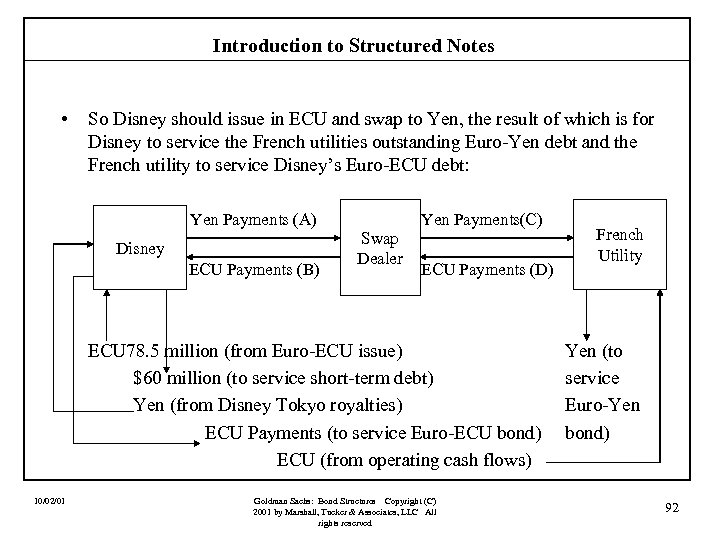Introduction to Structured Notes • So Disney should issue in ECU and swap to Yen, the result of which is for Disney to service the French utilities outstanding Euro-Yen debt and the French utility to service Disney’s Euro-ECU debt: Yen Payments (A) Disney ECU Payments (B) Swap Dealer Yen Payments(C) ECU Payments (D) ECU 78. 5 million (from Euro-ECU issue) $60 million (to service short-term debt) Yen (from Disney Tokyo royalties) ECU Payments (to service Euro-ECU bond) ECU (from operating cash flows) 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved French Utility Yen (to service Euro-Yen bond) 92

Introduction to Structured Notes • The next slide shows the actual cash flows on the swap. The swap dealer in this case turned out to be the Industrial Bank of Japan (IBJ), which was then AAA rated. (It could have been that the French utility demanded a bettercredited counter party than Goldman on the 10 -year swap. ) • The columns are labeled A, B, C and D and comport to the arrows labeled similarly in the previous slide. • When one computes the IRRs using the cash flows in the columns, one sees that Disney’s all-in funding cost in Yen (from issuing the Euro-ECU bond and swapping to Yen) was just 7. 01%. That is a savings of 74 bps versus using the Yen term loan (7. 75%). IBJ took 6 bps and therefore the French utility saved 2 bps (giving a total of 82 bps). • Conclusion: Disney funds in Yen at just 18 bps above a AAA despite being a weak single A. • Discuss IBJ’s “hari kari” swap. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 93

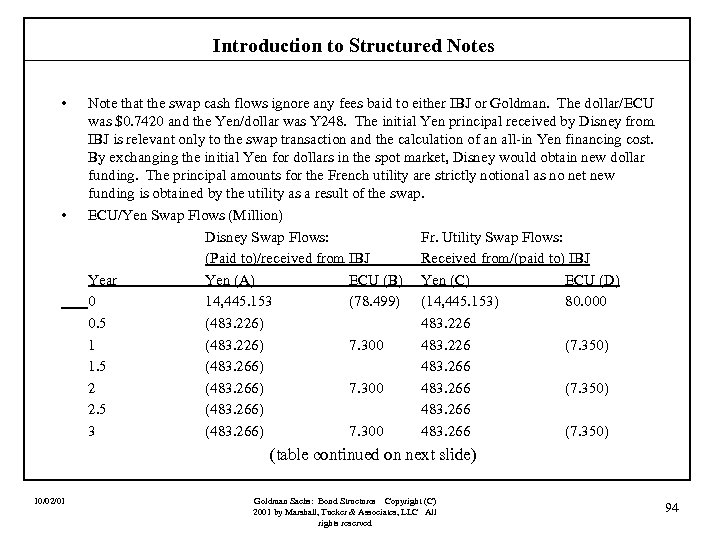Introduction to Structured Notes • • Note that the swap cash flows ignore any fees baid to either IBJ or Goldman. The dollar/ECU was $0. 7420 and the Yen/dollar was Y 248. The initial Yen principal received by Disney from IBJ is relevant only to the swap transaction and the calculation of an all-in Yen financing cost. By exchanging the initial Yen for dollars in the spot market, Disney would obtain new dollar funding. The principal amounts for the French utility are strictly notional as no net new funding is obtained by the utility as a result of the swap. ECU/Yen Swap Flows (Million) Disney Swap Flows: Fr. Utility Swap Flows: (Paid to)/received from IBJ Received from/(paid to) IBJ Year Yen (A) ECU (B) Yen (C) ECU (D) 0 14, 445. 153 (78. 499) (14, 445. 153) 80. 000 0. 5 (483. 226) 483. 226 1 (483. 226) 7. 300 483. 226 (7. 350) 1. 5 (483. 266) 483. 266 2 (483. 266) 7. 300 483. 266 (7. 350) 2. 5 (483. 266) 483. 266 3 (483. 266) 7. 300 483. 266 (7. 350) (table continued on next slide) 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 94

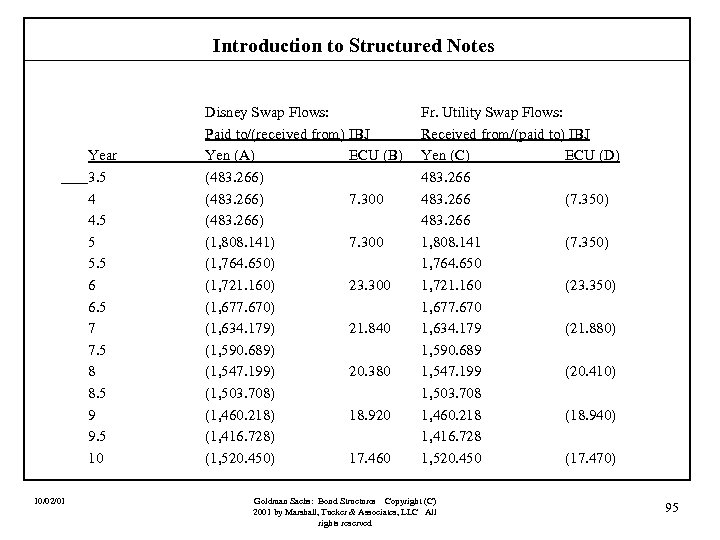Introduction to Structured Notes Year 3. 5 4 4. 5 5 5. 5 6 6. 5 7 7. 5 8 8. 5 9 9. 5 10 10/02/01 Disney Swap Flows: Paid to/(received from) IBJ Yen (A) ECU (B) (483. 266) 7. 300 (483. 266) (1, 808. 141) 7. 300 (1, 764. 650) (1, 721. 160) 23. 300 (1, 677. 670) (1, 634. 179) 21. 840 (1, 590. 689) (1, 547. 199) 20. 380 (1, 503. 708) (1, 460. 218) 18. 920 (1, 416. 728) (1, 520. 450) 17. 460 Fr. Utility Swap Flows: Received from/(paid to) IBJ Yen (C) ECU (D) 483. 266 (7. 350) 483. 266 1, 808. 141 (7. 350) 1, 764. 650 1, 721. 160 (23. 350) 1, 677. 670 1, 634. 179 (21. 880) 1, 590. 689 1, 547. 199 (20. 410) 1, 503. 708 1, 460. 218 (18. 940) 1, 416. 728 1, 520. 450 (17. 470) Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 95

Introduction to Structured Notes More Modern Applications: During the second half of the 1980 s and first half of the 1990 s, interest rate derivative desks discovered that the call option embedded in a callable bond could be replicated by a swaption. As a result, underwriters, working with their interest rate derivative desks, schooled corporate treasury officers on how to issue a callable bond and then sell-off (economically speaking) the embedded call by writing a swaption. If the embedded call could be purchased cheaply by the corporate issuer, that is, the added coupon was small compared to a straight-bond alternative, then the corporation’s overall funding cost would be lower (than the straight-debt alternative) after selling off the call by writing the swaption. At the end of the day, the embedded call was cheaper if its implied vol was lower than that of the swaption. We have: 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 96

Introduction to Structured Notes Issue callable bond + Write a swaption Issue straight debt (issue straight debt and buy back a call) (sell off embedded call) (lower coupon than issuing straight debt directly if the implied vol of the swaption is greater than that of the embedded call) Of course, the investment bank could help discover (or create) value for the buy-side under this same process. If the implied vol of the embedded call is greater than that of the swaption, then the investor - say a hedge fund that buys the debt issue under a 144 A offering - could buy the bond (possibly financing the purchase in the repo market) and buy the swaption. To isolate the value more precisely, the buyer could hedge the credit risk of the bond with a credit derivative. 10/02/01 Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 97

Introduction to Structured Notes • 10/02/01 Indeed, some now argue that the flood of embedded stock options accompanying these convertible issues has created a “volatility crush” or “volatility overhang” in the equity market. It is a fact that the market has been “taking out” time value from options, perhaps because of an excessive supply of vol. Volatility traders who have been delta and gamma neutral but carrying negative vegas have generally profited in 2001 (whereas such a strategy was generally a loser for the preceding five years). Goldman Sachs: Bond Structures Copyright (C) 2001 by Marshall, Tucker & Associates, LLC All rights reserved 98