Gödelian Foundations of Non-Computability and Heterogeneity In Economic

Gödelian Foundations of Non-Computability and Heterogeneity In Economic Forecasting and Strategic Innovation Sheri M. Markose Lecture 2 Economics Department and Centre For Computational Finance and Economic Agents (CCFEA) University of Essex, UK. scher@essex. ac. uk

ROAD MAP: I SELF-REFLEXIVE CONTRARIAN STRUCTURE : “This is false” The presence of contrarian payoff structures or hostile agents in a game theoretic framework are shown to result in the fundamental non-computable fixed point that corresponds to Gödel's undecidable proposition Lack of effective procedures to determine winning strategies in a stock market game with contrarian payoff structure Brian Arthur (1994): The Minority or El Farol game has a contrarian structure Results in the adoption of a multiplicity or heterogeneity of metamodels forecasting and strategizing by agents

ROAD MAP: II Game Theory with Hostile Agents: Nash Equilibrium is Surprise or Innovation Construction of fixed point or self-reference in so called rational expectations or mutual acknowledgement uses Diagonalization lemma and 2 nd Recursion Theorem Any best response function of the game which is constrained to be a total computable function then represents the productive function of the Emil Post (1944) set theoretic proof of the Gödel Incompleteness result. The productive function implements strategic innovation and objects of novelty or 'surprise' : formally maps into a non-recursively enumerable set This results in undecidable structure changing dynamics in the system

ROAD MAP: III Ubiquity of contrarian self-reflexive calculations in socio-economic systems Oppositional or contrarian structures, self-reflexive calculations and the necessity to innovate to out-smart hostile agents are ubiquitous in economic systems. As first noted in Binmore (1987) and Spear (1987), extant game theory and economic theory cannot model the strategic and logical necessity of Gödelian indeterminism in economic systems. Formal results developed in Markose (2002, 2004, 2005) on the implications of the Gödelian incompleteness result for economics. Keywords: Effective procedures; self-reflexivity; contrarian payoff structures; strategic innovation; Gödel Incompleteness.

Canonical Example of Self-Reflexive Systems and Contrarian Structures which have no computable fixed points • First example developed by Santa Fe Institute is the Artificial Stock Market (ASM) • Brian Arthur gave a powerful rebuttal of why traditional economic analysis will fail to understand stock markets and why ACE modelling is needed • In stock market an investor makes money if he/she can sell when everybody else is buying and buy when everybody else is selling. In other words, one needs to be in the minority or contrarian • Arthur called this the El Farol Bar problem. You want to go to the pub when it is not crowded. Assume everybody else wants to do the same. How can you rationally decide/strategize to succeed in this objective of being in the minority ? • If all of us have the same forecasting model to work out how many people will turn up – say our model says it will be 80% full – then as all of us do not want to be there when it is crowded – none of us will go. • This contradicts the prediction of our model and in fact we should go. If all reasoned this way – once again we will fail etc. So there is no Homogenous Rational Expectations and no rational way in which we can decide to go. Traditional economics cannot deal with this • Hence, Brian Arthur said we must use ACE models and see how the system dynamically selforganizes

Lack of a unique effective decision procedure : endogenous to the logic of the decision problem • Spear (1987) and Markose (2004, 2007) Non-computability of rational expectations equilibrium : RE as fixed point of market price function, g In a rational expectations equilibrium (REE) there exists some computable forecast function : f ^= fa such that fg(a) fa , (i) Then a is a fixed point of the market price function g. Note, a is the algorithm or program that computes the output of the market game when the price function g that determines the outcome is consistent with agents’ prediction functions for Pt+1. An agent has to find a meta forecast rule f ^= fa that satisfies (I). That is, the agent has to identify a proper subset of the set of all partial computable functions { f 0, f 1, f 2, . . . . }, such that only the fixed points of the total computable function g are identified, viz. { m | fg(m) = fm }. (II) By Rice’s Theorem no uniform recursive/ algorithmic procedure to identify set of indices in (ii). There is no systematic way of forming REs of the market price function g. Only inductive trial and error learning that begins search in an arbitrary subset of diverse forecast rules.

Self Reflexity in Stock Prices • • • “Agents , in facing the problem of choosing appropriate predictive models, face the same problem that statisticians face when choosing appropriate predictive models given a specific data set, but no objective means by which to choose a functional form…. The expectational models investors choose affect the price sequence, so that our statisticians very choices of model affect their data and so their choices of model” (ibid. p. 305, italics added). “In asset markets, agents’ forecasts create the world that agents are trying to forecast. Thus, asset markets have a reflexive nature in that prices are generated by traders’ expectations, but these expectations are formed on the basis of anticipation of others’ expectations. This reflexity, or selfreferential character of expectations, precludes expectations being formed by deductive means , so that perfect rationality ceases to be well defined” (Arthur et. al. 1997, Santa Fe Institute Working Paper We will proceed to show that instead of referring to the above self-reflexive problem as one that “ceases to be well defined ” – the problem is algorithmically unsolvable.

Example: II Design of Market Games: Should not permit computable winning strategies or Free Lunch • George Soros made £ 2 bn taking a short position against the Sterling and the Bank of England. He is alleged to have used the Liar or Contrarian Strategy. • Soros cut above ordinary speculator: student of Karl Popper and knows the self-reflexive problem of the Cretan Liar can subvert only from a a point of certainty or computable fixed point. Hence, if the policy position is perfectly known – hostile agents can destroy it. Indeterminism or ambiguity is a essential design element for success of market systems and zero sum games • Traffic Model and how to avoid congestion is a minority game

Part II: Main ingredients of a Nash Equilibrium With Surprise or Innovation I. III. Agents with full powers of Turing Machines: Why? Agents must have oppositional interests : Why? Arms Race Type Red Queen Dynamic: formally modelled as the productive function that can produce innovations ad infinitum

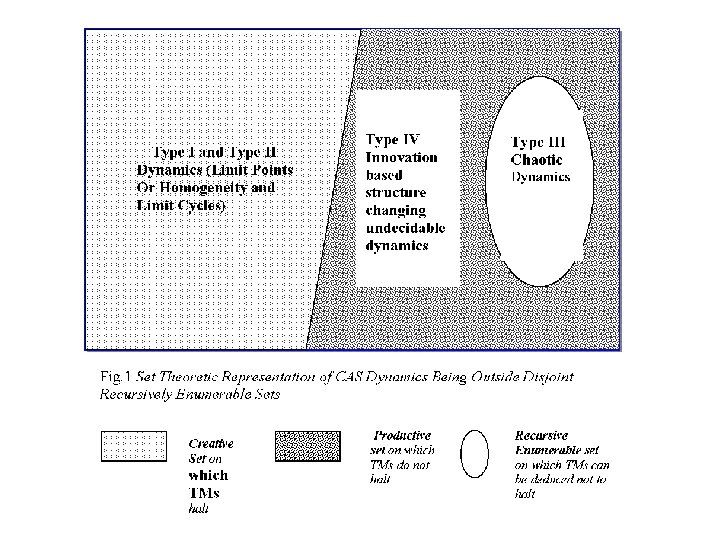
I. Agents with full powers of Turing Machines: Why? It is now well known from the Wolfram-Chomsky scheme (see, Wolfram, 1984, Foley, in Albin, 1998, pp. 42 -55, Markose, 2001 a) that on varying the computational capabilities of agents, different system wide or global dynamics can be generated. Finite automata produce Type 1 dynamics with unique limit points; Push down automata produce Type 2 dynamics with limit cycles; Linear bounded automata produce Type 3 chaotic output trajectories with strange attractors. However, it takes agents with full powers of Turing Machines capable of simulating other Turing machines and hence self-reference, a property called computational universality, to produce the Type 4 irregular innovation based structure changing dynamics associated with capitalist growth.

II. Agents must have oppositional interests. Why? Axelrod (1987) in his classic study on cooperative and noncooperative behaviour in governing design principles behind evolution had raised this crucial question on the necessity of hostile agents : “ we can begin asking about whether parasites are inherent to all complex systems, or merely the outcome of the way biological systems have happened to evolve” (ibid. p. 41). It is believed that with the computational theory of actor innovation (Markose, 2003/4), we have a formal solution of one of the long standing mysteries as to why agents with the highest level of computational intelligence are necessary to produce innovative outcomes in Type IV dynamics.

Finally what do non-computable emergent equilibria look like? It corresponds to the famous Langton thesis on “life at the edge of chaos” and is formally identical to recursively inseparable sets first discovered in the context of formally undecidable propositions and algorithmically unsolvable problems by Post (1944). Figure 1 gives the set theoretic representation of the Wolfram-Chomsky schema of complexity classes for dynamical systems which formally corresponds to Post’s set theoretic proof of Gödel Incompleteness Result.

Mathematical Preliminaries MECHANISM, ALGORITHM, COMPUTATION The Church Turing Thesis states that models of computation considered so far for implementing finitely encoded instructions, prominent among these being that of the Turing machine (T. M for short), have all been shown to be equivalent to the class of general recursive functions.

Definition 2: A set which is the null set or the domain or the range of a recursive function is a recursively enumerable (r. e) set. Sets that cannot be enumerated by T. Ms are not r. e. The one feature of computability theory that is crucial to eductive game theory where players have to simulate the decision procedure of other players, is the notion of the Universal Turing Machine(UTM). (2) The UTM, on L. H. S of (2) on input x will halt and output what the TMa on the RHS does when the latter halts and otherwise both are undefined.

. C = { x | fx(x) ) ; TMx(x) halts ; x Wx } (3. a) The complement of C C~ = { x | TMx (x) does not halt; fx(x) not defined; x Ï Wx} (3. b). Theorem 1: The set C~ is not recursively enumerable. In the proof that C~ is not recursively enumerable, viz there is no computable function that will enumerate it, Cantor’s diagonalization method is used. [2] Assume that there is a computable function f = fy , whose domain Wy = C~. Now, if y Wy , then y C~ as we have assumed C~ = Wy. But by the definition of C~ in (3. b) if y Wy , then y C and not to C~. Alternatively, if yÏWy , y ÏC~ , given the assumption that C~ = Wy. Then, again we have a contradiction, as since from (3. b) when yÏ Wy , y C~. Thus we have to reject the assumption that for some computable function f = fy , its domain Wy= C~.

Definition 5: A creative set Q is a recursively enumerable set whose compliment, Q~, is a productive set. The set Q~ is productive if there exists a recursively enumerable set Wx disjoint from Q (viz. Wx Ì Q~) and there is a total computable function f(x) which belongs to Q~ - Wx. f(x) Q~ – Wx is referred to as the productive function and is a ‘witness’ to the fact that Q~ is not recursively enumerable. Any effective enumeration of Q~ will fail to list f(x), Cutland (1980, p. 134 -136).

GAME: REGULATORY ARBITRAGE OR PARASITE AND HOST MODEL UNDER COMPUTABILITY CONSTRAINTS Computability constraints means that all decision rules, actions etc. are finitely encodable procedures with Godel numbers (g. ns). G= {(p, q), (Ap, Ag), s S}. This information is in the public domain. Here, (p, g) denote the respective g. ns of the objective functions, to be specified, of players, p, the private sector/regulatee and g, government/regulator. The action sets by Ai with A= Ai, are finitely countable with ail Ai , i (g, p) being the g. n of an action rule of player i and l=0, 1, 2, . . . , L. An element s S denotes a finite vector of state variables and other archival information and S is a finitely countable set. The strategy functions denoted by (bg , bp ) The strategy sets containing the g. ns of computable strategies denoted by (Bp, Bg). Lower case b are g. n for strategies and b^ beliefs of other players strategy.

LIKE CHESS NOTATION: META ANALYSIS OF GAME All meta-information with regard to the outcomes of the game for any given set of state variables, s belong to S and state of play can be effectively organized by the so called prediction function f s (x, y) (s) in an infinite matrix X of the enumeration of all computable functions, given in Figure 2.

FIGURE 2 PREDICTABLE PAYOFFS X 0 fs(0, 0) fs (0, 1) fs (0, 2) fs (0, 3) X 1 fs(1, 0) fs (1, 1) fs (1, 2) fs (1, 3) X 2 fs(2, 0) fs (2, 1) fs (2, 2) fs (1, 3). . Xx fs(x, 0) fs (x, 1) fs (x, 2) fs (x, 3) . . fs(0, y) . . . . fs(1, y) . . . . fs(2, y) . . fs(x, y) . . fs(x, x) The best response function fi can dynamically move the system from row to row. f s (x, y) (s) = q. q in some code, is the vector of state variables determining the outcome of the game. Nash Equilibria are DIAGONAL ELEMENTS s(x, y) is the index of the program for prediction function f that produces the output of the game when one player plays strategy x and the other plays a strategy that is consistent with his belief that the first player has used strategy y.

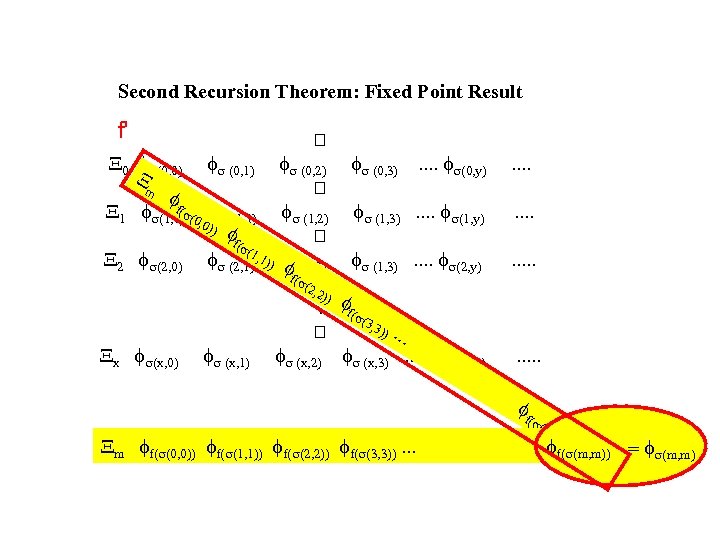
Second Recursion Theorem: Fixed Point Result f' X 0 fs(0, 0) fs (0, 1) fs (0, 2) fs (0, 3). . fs(0, y) X m ff ( X 1 fs(1, 0)s(0, fs (1, 1) fs (1, 2) fs (1, 3). . fs(1, y) 0)) ff (s( X 2 fs(2, 0) fs (2, 1)1, 1)) fs (2, 2) fs (1, 3). . fs(2, y) ff (s(. 2, 2 )) . ff(s( 3, 3 )). . . Xx fs(x, 0) fs (x, 1) fs (x, 2) fs (x, 3). . fs(x, x ) . . . . ff Xm ff(s(0, 0)) ff(s(1, 1)) ff(s(2, 2)) ff(s(3, 3)). . . (s( m , m )) ff(s(m, m)) = fs(m, m)

Theorem 1: The representational system is a 1 -1 mapping between meta information in matrix X in Figure 2 and internal calculations such that the conditions under which the prediction function which determines the output of the game for each (x, y) point is defined as follows:

Definition 5: The best response functions fi, i (p, g) that are total computable functions can belong to one of the following classes – such that the g. ns of fi are contained in set , = { m | f j = f m , fm is total computable}. (5. b) Remark 4: The set which is the set of all total computable functions is not recursively enumerable. The proof of this is standard, see, Cutland (1980, p. 7). As will be clear, (5. b) draws attention to issues on how innovative actions/institutions can be constructed from existing action sets.

Definition 7 : The objective functions of players are computable functions Pi , i (p, g) defined over the partial recursive payoff/outcome functions specified in state variables in (3). The Nash equilibrium strategies with g. ns denoted by (bp. E, bg E) entail two subroutines or iterations, to be specified later.

In standard rational choice models of game theory, the optimization calculus in the choice of best response requires choice to be restricted to given actions sets. Hence, strategy functions map from a relevant tuple that encodes meta information of the game into given action sets bi ( fis(x, x), z, s, A) Ai and fi= f m , m Ai, i (p, g) . (7. a) Unless this is the case, as the set is not recursively enumerable there is in general no computable decision procedure that enables a player to determine the other player’s response functions. Definition 7: We say that the player has used a strategic innovation or a surprise and adopted an innovation in terms of actions from - A, viz. outside given action sets when, bi (fis(x, x)), z, s, A) - A and fi = fi ! = fm , m -A, i (p, g). (7. b)

WHEN DOES THIS HAPPEN? The very function of the Gödel meta framework is to ensure that no move in the game made by rational and calculating players can entail an unpredictable/surprise response function from set unless players can mutually infer by strictly codifiable deductive means from s(x. x) that (7. b) is a logical implication of the optimal strategy at the point in the game. In other words, the necessity of an innovative/surprise strategy as a best response and that an algorithmic decision procedure is impossible at this point are fully codifiable propositions in the meta analysis of the game.

THE STRUCTURE OF OPPOSITION: THE LIAR STRATEGY For any state s when the rule a applies, THE LIAR STRATEGY fp¬ : For all s when policy rule a does not apply, fp¬ = 0 . Do Nothing (14. b) Implications of the Liar Strategy

Proposition 3: The outcome of the game at this out of equilibrium point s(ba ¬, ba ) is predictable with The no-win for g is recursively ascertainable and rule a cannot be a Nash equilibrium strategy for g. Not acknowledging the identity of the Liar is fatal for transparent rules and the success of the Liar entails an elementary error in logic and game theory on part of the other player.

3. 3 The Non-computable Fixed Point Now, if g acknowledges the identity of the Liar in (14. a), he updates his belief with ba¬ , the code for the Liar strategy in (14. a). Once the identity of the Liar has been acknowledged, g must rationally abandon the transparent rule a in (14. a) as per Proposition 3. Theorem 3: The prediction function indexed by the fixed point of the Liar/rule breaker best response function fp¬ in (15) is not computable. Here, the fixed point which signals mutual knowledge that p will falsify predicted outcomes of g’s rule will lack structural invariance relative to the best response function fp¬ whose fixed point it is. Herbert Simon calls this the outguessing problem

3. 4 Surprise Nash Equilibria and The Productive Function g’s Nash equilibrium strategy bg. E with g. n bg. E implemented by the total computable function b 1 in (11. a) must be such that bg. E (fgs (ba¬ , ba¬ ), z, s, A) - A and fg = fg! = fm , m -A. (16. a) That is, fg! implements an innovation and bg. E ! is the g. n of the surprise strategy function in (16. a).

Likewise for player p, fp! implements an innovation in (16. b) and bp. E ! is the g. n of the surprise strategy function. Thus, bp. E (fp s (b 1( ba¬), b 1( ba¬ )), z, s, A) - A and fp = fp ! = fm , m -A. (16. b) The total computable functions (b 1 , b 2 ) in (11. a, b) implementing the g. ns of the respective Nash equilibrium strategies from the uncomputable fixed point in (15), fully definable in the meta analysis, can only map into domains of respective strategy sets (Bp , Bg) whose members cannot be recursively enumerable. As fp are total computable functions thereoff, it can only map into the productive set -A, which is not recursively enumerable.

Theorem 5 The incompleteness of p’s strategy set Bp that arises from the agency of the Liar strategy : requires the proof that ßp+c is productive as in Definition 4 with the g. n of the surprise strategy: bp. E ! ßp+c - ßp¬. Construct a witness for why ßp+c is not recursively enumerable.

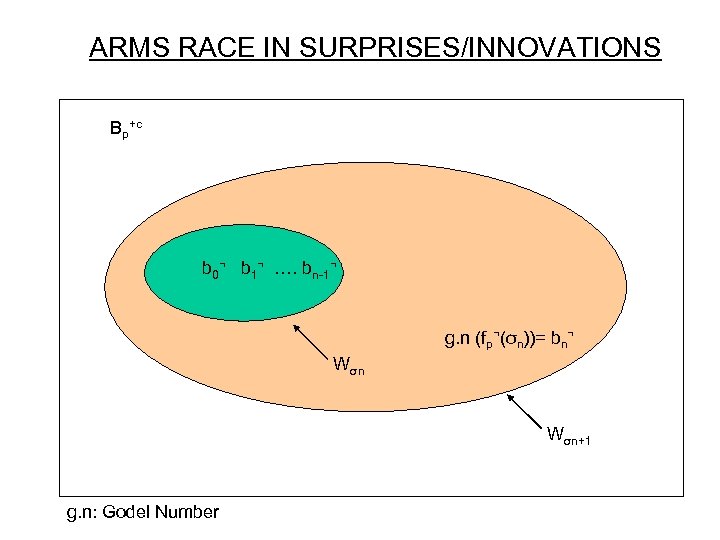
ARMS RACE IN SURPRISES/INNOVATIONS Bp+c b 0¬ b 1¬ …. bn-1¬ g. n (fp¬(σn))= bn¬ Wσn+1 g. n: Godel Number

CONCLUDING REMARKS INNOVATION FAR FROM BEING A RANDOM OUTCOME, AS IS POPULARLY HELD, IS THE RESULT PRIMARILY OF COMPUTATONAL INTELLIGENCE Wolfram (1984) had conjectured that the highest level of computational intelligence, the capacity for self-referential calculation of hostile behaviour was also necessary. This casts doubt on the Darwinian tradition that random mutation is the only source of variety THE STRUCTURE OF OPPOSITION IS A LOGICAL NECESSARY CONDITION FOR INNOVATION TO BE A STRATEGIC RATIONAL OUTCOME AND A NASH EQUILBRIUM OF A GAME.

• Surprise Nash equilbria correspond to phase transition of “life at the edge of chaos”. • In Markose (2003) it is argued that for systems to stay at the phase transition associated wih novelty production requires the Red Queen dynamic of rivalrous coevolving species. In the Ray’s Tierra(1992) and Hillis ( 1992)artificial life simulation models, once computational agents have enough capabilities to detect rivalrous behaviour that is inimical to them, they learn to use secrecy and surprises. • Finally, a matter that is beyond this paper, but is of crucial mathematical importance is that objects of adaptive novelty as in the Gödel (1931) result has the highest diophantine degree of algorithmic unsolvability of the Hilbert Tenth problem. This model of indeterminism is a far cry from extant models that appear to assume adaptive innovation or strategic ‘surprise’ is white noise which in the framework of entropy represents perfect disorder, the antithesis of selforganized complexity. It can be conjectured that a lack of progress in our understanding of market incompleteness and arbitrage free institutions is related to these issues on indeterminism.

Selected References • • Arthur, W. B. , (1994). 'Inductive Behaviour and Bounded Rationality', American Economic Review, 84, pp. 406 -411. Binmore, K. (1987), 'Modelling Rational Players: Part 1', Journal of Economics and Philosophy, vol. 3, pp. 179 -214. Markose, S. M, 2005 , 'Computability and Evolutionary Complexity : Markets as Complex Adaptive Systems (CAS)', Economic Journal , vol. 115, pp. F 159 -F 192. Markose, S. M, 2004, 'Novelty in Complex Adaptive Systems (CAS): A Computational Theory of Actor Innovation', Physica A: Statistical Mechanics and Its Applications, vol. 344, pp. 41 - 49. Fuller details in University of Essex, Economics Dept. Discussion Paper No. 575, January 2004. Markose, S. M. , July 2002, 'The New Evolutionary Computational Paradigm of Complex Adaptive Systems: Challenges and Prospects For Economics and Finance', In, Genetic Algorithms and Genetic Programming in Computational Finance, Edited by Shu-Heng Chen, Kluwer Academic Publishers, pp. 443 -484. Also Essex University Economics Department DP no. 552, July 2001. Post, E. (1944). 'Recursively Enumerable Sets of Positive Integers and Their Decision Problems', Bulletin of American Mathematical Society, vol. 50, pp. 284 -316. Spear, S. (1989), 'Learning Rational Expectations Under Computability Constraints', Econometrica , vol. 57, pp. 889 -910.