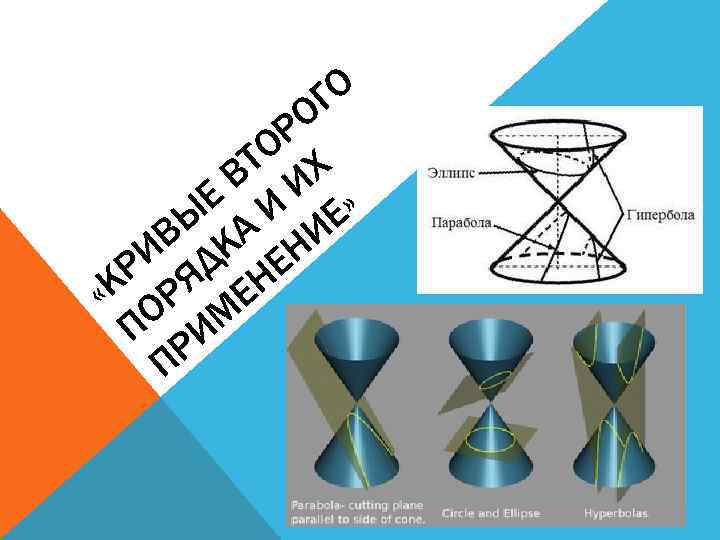
 ГО О Р ТО Х В И Е» Ы А И В К Н И Д Е Р Я Н «К ОР Е П РИМ П
ГО О Р ТО Х В И Е» Ы А И В К Н И Д Е Р Я Н «К ОР Е П РИМ П
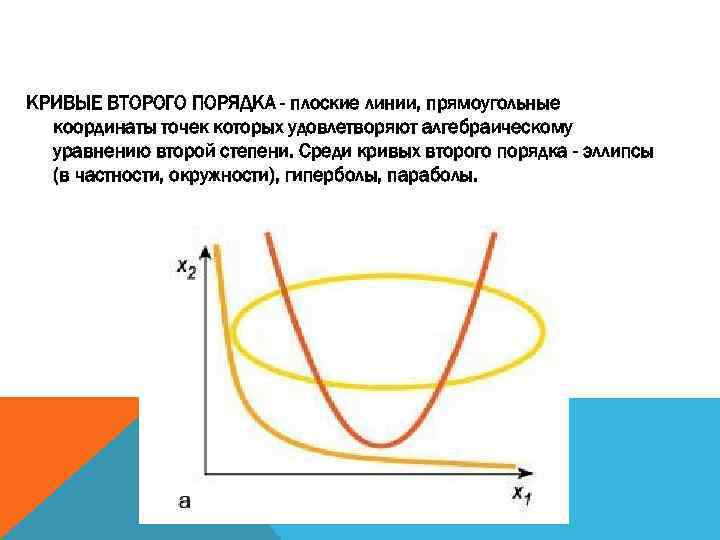 КРИВЫЕ ВТОРОГО ПОРЯДКА - плоские линии, прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению второй степени. Среди кривых второго порядка - эллипсы (в частности, окружности), гиперболы, параболы.
КРИВЫЕ ВТОРОГО ПОРЯДКА - плоские линии, прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению второй степени. Среди кривых второго порядка - эллипсы (в частности, окружности), гиперболы, параболы.
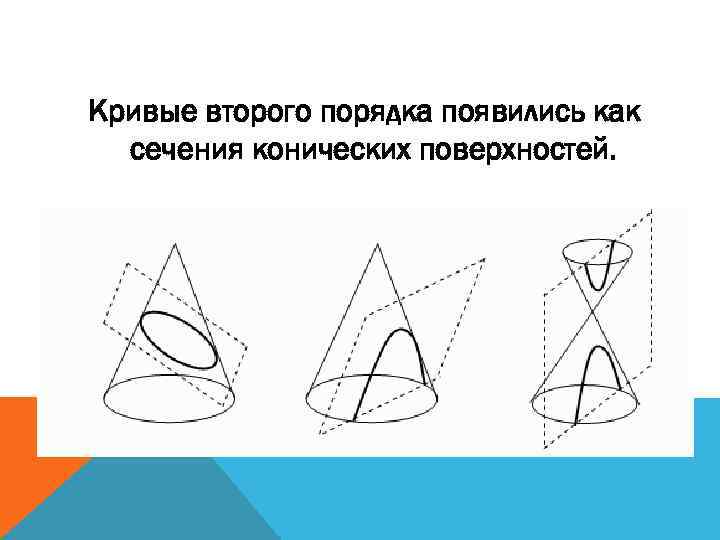 Кривые второго порядка появились как сечения конических поверхностей.
Кривые второго порядка появились как сечения конических поверхностей.
 Одним из первых, кто начал изучать конические сечения — эллипс, парабола, гипербола, был ученик знаменитого Платона, древнегреческий математик Менехм (IV в. до н. э. ). Изменяя угол при вершине прямого кругового конуса, Менехм получил три вида кривых: эллипс — если угол при вершине конуса острый; парабола — если угол прямой; одну ветвь гиперболы — если угол тупой. КОНИЧЕСКИЕ СЕЧЕНИЯ: КРУГ, ЭЛЛИПС, ПАРАБОЛА, ГИПЕРБОЛА
Одним из первых, кто начал изучать конические сечения — эллипс, парабола, гипербола, был ученик знаменитого Платона, древнегреческий математик Менехм (IV в. до н. э. ). Изменяя угол при вершине прямого кругового конуса, Менехм получил три вида кривых: эллипс — если угол при вершине конуса острый; парабола — если угол прямой; одну ветвь гиперболы — если угол тупой. КОНИЧЕСКИЕ СЕЧЕНИЯ: КРУГ, ЭЛЛИПС, ПАРАБОЛА, ГИПЕРБОЛА
 Кеплер, наблюдая за видимыми перемещениями планет на небесной сфере, открыл три закона, один из которых устанавливает, что каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Ньютон не только теоретически обосновал законы движения планет, но и доказал, что каждое тело под действием притяжения другого тела может двигаться только по эллипсу, либо по параболе, либо по гиперболе. В частности, по этим кривым происходит движение всех комет Солнечной системы.
Кеплер, наблюдая за видимыми перемещениями планет на небесной сфере, открыл три закона, один из которых устанавливает, что каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Ньютон не только теоретически обосновал законы движения планет, но и доказал, что каждое тело под действием притяжения другого тела может двигаться только по эллипсу, либо по параболе, либо по гиперболе. В частности, по этим кривым происходит движение всех комет Солнечной системы.
 Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. а) А 1, А 2, В 1, В 2 – вершины эллипса. б) ОА 2 – большая полуось. в) ОВ 1 – малая полуось.
Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. а) А 1, А 2, В 1, В 2 – вершины эллипса. б) ОА 2 – большая полуось. в) ОВ 1 – малая полуось.
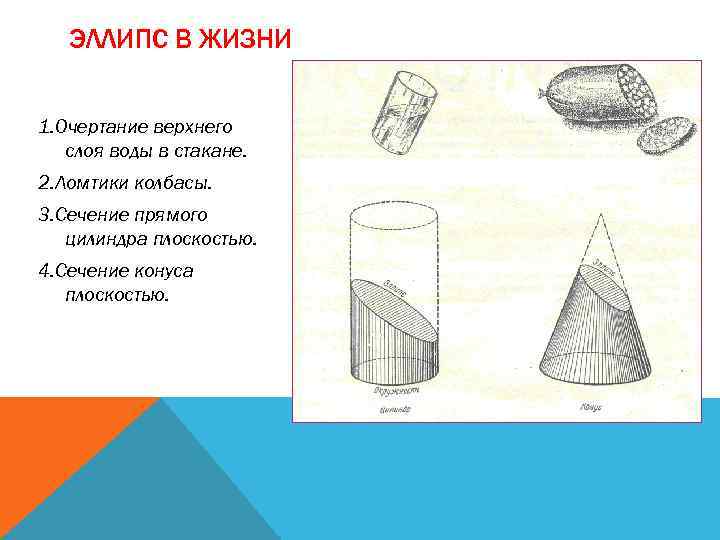 ЭЛЛИПС В ЖИЗНИ 1. Очертание верхнего слоя воды в стакане. 2. Ломтики колбасы. 3. Сечение прямого цилиндра плоскостью. 4. Сечение конуса плоскостью.
ЭЛЛИПС В ЖИЗНИ 1. Очертание верхнего слоя воды в стакане. 2. Ломтики колбасы. 3. Сечение прямого цилиндра плоскостью. 4. Сечение конуса плоскостью.
 Замечательное оптическое свойство эллипса лежит в основе интересного акустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека , стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя расстояние на самом деле велико.
Замечательное оптическое свойство эллипса лежит в основе интересного акустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека , стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя расстояние на самом деле велико.
 ЭЛЛИПС В АРХИТЕКТУРНОМ МИРЕ Естественный эллипс. Токио, Япония. Этот уникальный дом расположен в густо населенном районе Токио, который славится своими магазинами и ночной жизнью. Задача архитектора заключалась в том, чтобы оградить жителей дома от света и шума, не отрывая при этом дом от окружающего мира. Шарообразную форму здания образуют двадцать четыре овальных кольца, вертикально закрепленных вокруг полого эллиптического цилиндра.
ЭЛЛИПС В АРХИТЕКТУРНОМ МИРЕ Естественный эллипс. Токио, Япония. Этот уникальный дом расположен в густо населенном районе Токио, который славится своими магазинами и ночной жизнью. Задача архитектора заключалась в том, чтобы оградить жителей дома от света и шума, не отрывая при этом дом от окружающего мира. Шарообразную форму здания образуют двадцать четыре овальных кольца, вертикально закрепленных вокруг полого эллиптического цилиндра.
 КОЛИЗЕЙ
КОЛИЗЕЙ
 АМФИТЕАТР В ВЕРОНЕ
АМФИТЕАТР В ВЕРОНЕ
 Подобно другим римским амфитеатрам, Амфитеатр Флавиев представляет в плане эллипс, середина которого занята ареной (также эллиптической формы) и окружающими её концентрическими кольцами мест для зрителей. От всех сооружений такого рода Колизей отличается своей величиной.
Подобно другим римским амфитеатрам, Амфитеатр Флавиев представляет в плане эллипс, середина которого занята ареной (также эллиптической формы) и окружающими её концентрическими кольцами мест для зрителей. От всех сооружений такого рода Колизей отличается своей величиной.
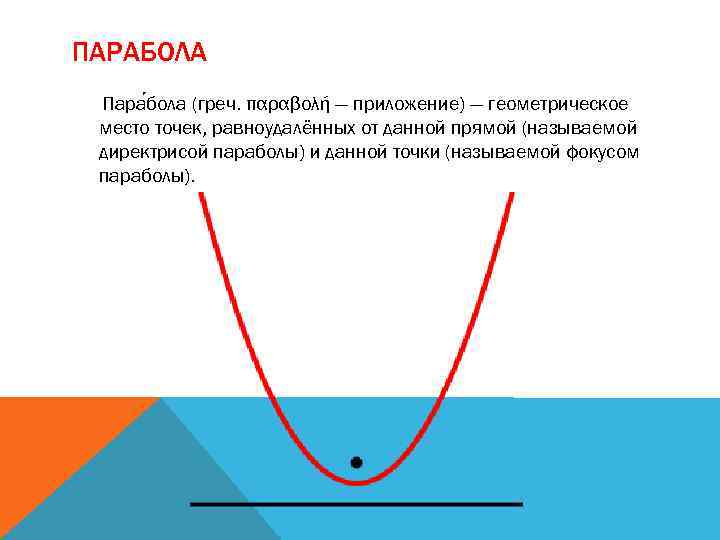 ПАРАБОЛА Пара бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
ПАРАБОЛА Пара бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
 Если вращать параболу вокруг ее оси вращения то получится поверхность, которую называют параболоид вращения. Если сильно размешать ложечкой воду в стакане, а потом вынуть ложечку, то поверхность воды примет форму такого параболоида.
Если вращать параболу вокруг ее оси вращения то получится поверхность, которую называют параболоид вращения. Если сильно размешать ложечкой воду в стакане, а потом вынуть ложечку, то поверхность воды примет форму такого параболоида.
 Парабола обладает оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Если в фокусе параболы поместить источник света, то все лучи от него, отразившись от параболы, пойдут параллельно ее оси.
Парабола обладает оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Если в фокусе параболы поместить источник света, то все лучи от него, отразившись от параболы, пойдут параллельно ее оси.
 И наоборот: если на параболу направить пучок лучей, параллельных оси, то после отражения все лучи соберутся в фокусе параболы.
И наоборот: если на параболу направить пучок лучей, параллельных оси, то после отражения все лучи соберутся в фокусе параболы.
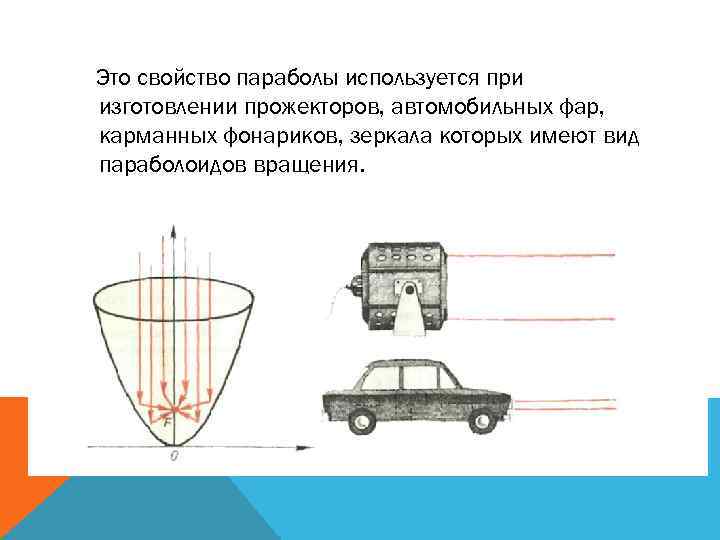 Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения.
Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения.
 НЕ ХОТИТЕ ПОКАТАТЬСЯ? Если вращать большой параболоид, то каждому из людей, разместившихся внутри него, кажется, что он сам твердо стоит на полу, а все остальные люди какимто чудом держатся на стенках.
НЕ ХОТИТЕ ПОКАТАТЬСЯ? Если вращать большой параболоид, то каждому из людей, разместившихся внутри него, кажется, что он сам твердо стоит на полу, а все остальные люди какимто чудом держатся на стенках.
 СОЛНЕЧНАЯ ЗАЖИГАЛКА Оригинальный способ использования энергии Солнца. Солнечная зажигалка представляет собой параболическое зеркало из нержавеющей стали, почти такое же, как-то, которое используется для зажигания Олимпийского огня в Афинах. Параболическое зеркало дает возможность собрать всю энергию в одной фокусной точке и зажечь огонь. Температура в этой точке может достигать 537 -ми градусов по Цельсию. Такое устройство будет незаменимо в походе и в других полевых условиях.
СОЛНЕЧНАЯ ЗАЖИГАЛКА Оригинальный способ использования энергии Солнца. Солнечная зажигалка представляет собой параболическое зеркало из нержавеющей стали, почти такое же, как-то, которое используется для зажигания Олимпийского огня в Афинах. Параболическое зеркало дает возможность собрать всю энергию в одной фокусной точке и зажечь огонь. Температура в этой точке может достигать 537 -ми градусов по Цельсию. Такое устройство будет незаменимо в походе и в других полевых условиях.
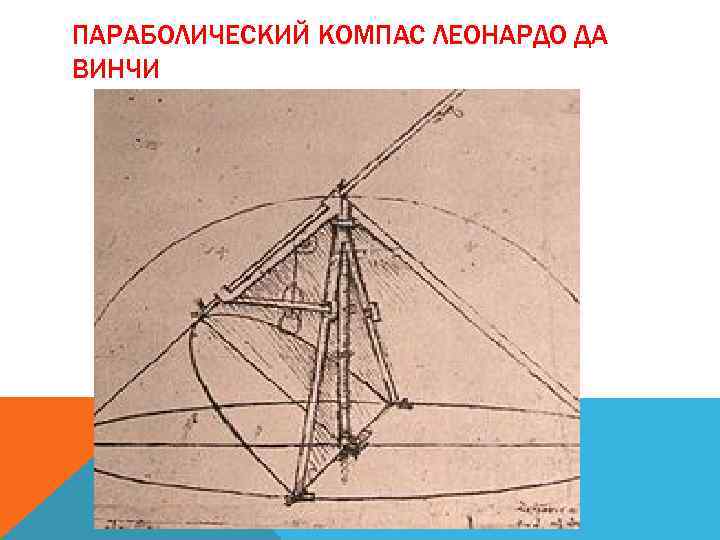 ПАРАБОЛИЧЕСКИЙ КОМПАС ЛЕОНАРДО ДА ВИНЧИ
ПАРАБОЛИЧЕСКИЙ КОМПАС ЛЕОНАРДО ДА ВИНЧИ
 ПАРАБОЛИЧЕСКАЯ СОЛНЕЧНАЯ ЭЛЕКТРОСТАНЦИЯ В КАЛИФОРНИИ, США
ПАРАБОЛИЧЕСКАЯ СОЛНЕЧНАЯ ЭЛЕКТРОСТАНЦИЯ В КАЛИФОРНИИ, США
 ПАРАБОЛИЧЕСКИЕ ТРАЕКТОРИИ СТРУЙ ВОДЫ
ПАРАБОЛИЧЕСКИЕ ТРАЕКТОРИИ СТРУЙ ВОДЫ
 ПРИМЕНЕНИЕ ПАРАБОЛЫ В БАЛЛИСТИКЕ Баллистика (от греч. pa. Msiv— бросать) — наука о движении тел, брошенных в пространстве, основанная на математике и физике. Она занимается, главным образом, исследованием движения снарядов, выпущенных из огнестрельного оружия, ракетных снарядов и баллистических ракет. Различают внутреннюю баллистику, занимающуюся исследованием движения снаряда в канале орудия, в противоположность внешней баллистике, исследующей движение снаряда по выходу из орудия. Под внешней баллистикой понимают, как правило, науку о движении тел в воздушном и безвоздушном пространстве под действием только внешних сил.
ПРИМЕНЕНИЕ ПАРАБОЛЫ В БАЛЛИСТИКЕ Баллистика (от греч. pa. Msiv— бросать) — наука о движении тел, брошенных в пространстве, основанная на математике и физике. Она занимается, главным образом, исследованием движения снарядов, выпущенных из огнестрельного оружия, ракетных снарядов и баллистических ракет. Различают внутреннюю баллистику, занимающуюся исследованием движения снаряда в канале орудия, в противоположность внешней баллистике, исследующей движение снаряда по выходу из орудия. Под внешней баллистикой понимают, как правило, науку о движении тел в воздушном и безвоздушном пространстве под действием только внешних сил.
 ТРАЕКТОРИИ ПРЫЖКОВ ЖИВОТНЫХ БЛИЗКИ К ПАРАБОЛЕ
ТРАЕКТОРИИ ПРЫЖКОВ ЖИВОТНЫХ БЛИЗКИ К ПАРАБОЛЕ
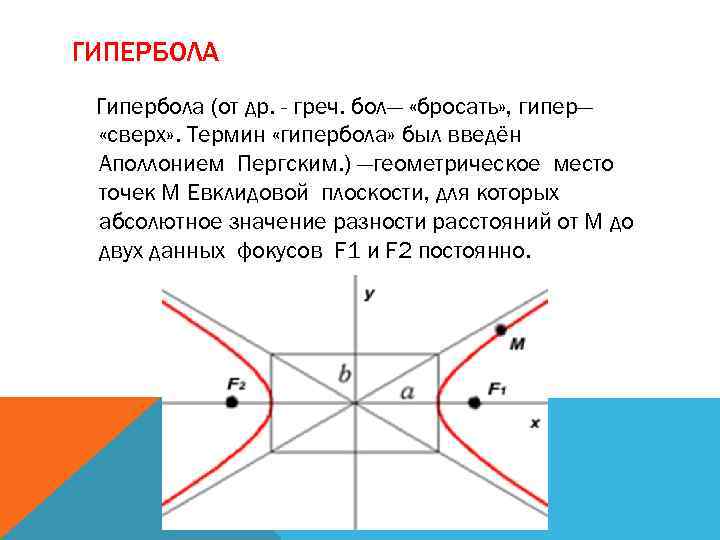 ГИПЕРБОЛА Гипербола (от др. - греч. бол— «бросать» , гипер— «сверх» . Термин «гипербола» был введён Аполлонием Пергским. ) —геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух данных фокусов F 1 и F 2 постоянно.
ГИПЕРБОЛА Гипербола (от др. - греч. бол— «бросать» , гипер— «сверх» . Термин «гипербола» был введён Аполлонием Пергским. ) —геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух данных фокусов F 1 и F 2 постоянно.
 Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.
 Траектории некоторых космических тел, проходящих вблизи звезды или другого массивного объекта на достаточно большой скорости могут имеют форму гиперболы. С помощью гиперболы военные определяют, как нужно направить орудие, чтобы поразить неподвижную звучащую цель, например, стреляющее орудие противника.
Траектории некоторых космических тел, проходящих вблизи звезды или другого массивного объекта на достаточно большой скорости могут имеют форму гиперболы. С помощью гиперболы военные определяют, как нужно направить орудие, чтобы поразить неподвижную звучащую цель, например, стреляющее орудие противника.
 Крылья бабочки напоминают форму гиперболы
Крылья бабочки напоминают форму гиперболы
 Формы мостов делают так, что воображаемое продольное сечение их вертикальной плоскостью – кривая линия, близка к гиперболе.
Формы мостов делают так, что воображаемое продольное сечение их вертикальной плоскостью – кривая линия, близка к гиперболе.
 Свойства гиперболоида использовали при строительстве Эйфелевой башни в Париже.
Свойства гиперболоида использовали при строительстве Эйфелевой башни в Париже.
 Геометрические свойства кривых используются в повседневной жизни. Применение кривых широко распространенно, их применяют в производстве, строительстве, военном деле и т. д. Трудно себе представить мир без этих кривых, хоть они так не заметны для нашего повседневного взора.
Геометрические свойства кривых используются в повседневной жизни. Применение кривых широко распространенно, их применяют в производстве, строительстве, военном деле и т. д. Трудно себе представить мир без этих кривых, хоть они так не заметны для нашего повседневного взора.


