edab0a70441bccb9d1caa7eb03d7cbd0.ppt
- Количество слайдов: 14

ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) МОДЕЛЬ УСТЬИЧНОЙ РЕГУЛЯЦИИ КАК ЗАДАЧА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ А. Г. Топаж
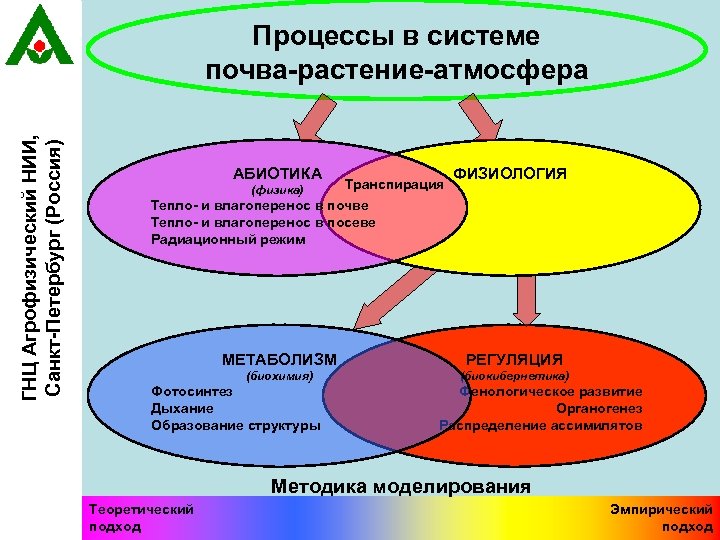
ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Процессы в системе почва-растение-атмосфера АБИОТИКА (физика) Транспирация ФИЗИОЛОГИЯ Тепло- и влагоперенос в почве Тепло- и влагоперенос в посеве Радиационный режим МЕТАБОЛИЗМ РЕГУЛЯЦИЯ (биохимия) (биокибернетика) Фотосинтез Дыхание Образование структуры Фенологическое развитие Органогенез Распределение ассимилятов Методика моделирования Теоретический подход Эмпирический подход

ОСНОВНЫЕ ПОСТУЛАТЫ ПАРАДИГМЫ ПРИНЦИПА ОПТИМАЛЬНОСТИ ДЛЯ ОПИСАНИЯ ПРОЦЕССОВ РЕГУЛЯЦИИ ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) v Растение рассматривается как сложная открытая динамическая система (развивающийся и циклически воспроизводящийся механизм) с определенной целью своего функционирования. v Цель формулируется в интерпретируемых терминах воспроизводства наиболее многочисленного и жизнеспособного потомства. v Законы метаболизма (производства и транспорта структурных веществ внутри растения) известны и неизменны. Они, в определенном смысле, представляют собой ограничения, формирующие допустимый набор траекторий развития. v Конкретный исследуемый процесс регуляции интерпретируется как программа управления метаболизмом. Он представляет собой набор директив по внешним условиям и динамических обратных связей по внутренним переменным. v Целью регуляции (управления) является достижение оптимального показателя поставленной цели, т. е. она служит решением некоторой обобщенной задачи оптимизации.
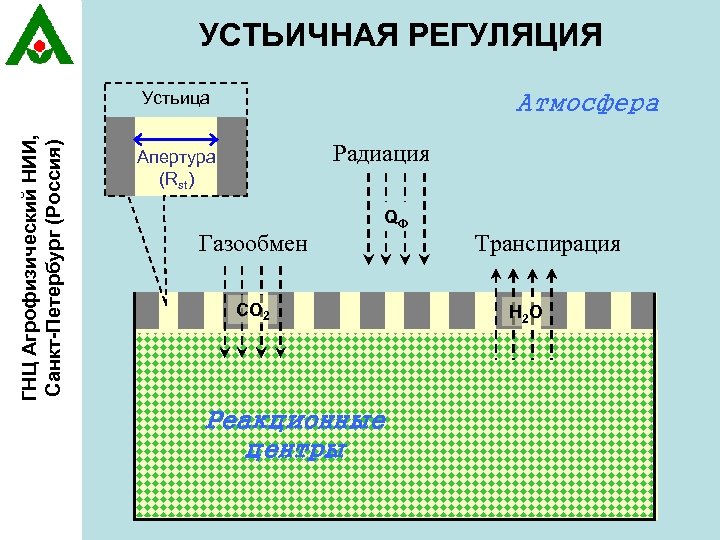
УСТЬИЧНАЯ РЕГУЛЯЦИЯ ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Устьица Атмосфера Радиация Апертура (Rst) Газообмен QФ CO 2 Реакционные центры Транспирация H 2 O

Факты и предположения ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) v Уровень открытия устьиц ОДНОВРЕМЕННО управляет интенсивностью газообмена и транспирации v Целями оптимальной программы устьичной регуляции являются: v Максимизация фотосинтеза (газообмена) v Минимизация ? ? ? транспирации v Уменьшение транспирации ведет к перегреву листа, что может являться отрицательным фактором v Увеличение транспирации ведет к потере почвенной влаги, то есть к потенциальной опасности засухи. v Адекватной «физиологической» модели для описания прямого негативного влияния засухи на процессы жизнедеятельности растения пока не разработано. v «Оптимальная» устьичная регуляция должна обеспечивать функциональный баланс между газообменом и транспирацией.

Физика процесса фотосинтеза ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Нетто-ассимиляция (производство первичных углеродных ассимилятов): Фотосинтез: Дыхание:

Физика процесса транспирации ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Радиационный баланс: Поглощение воды корнями: Водный баланс: E Er ; R = leaf
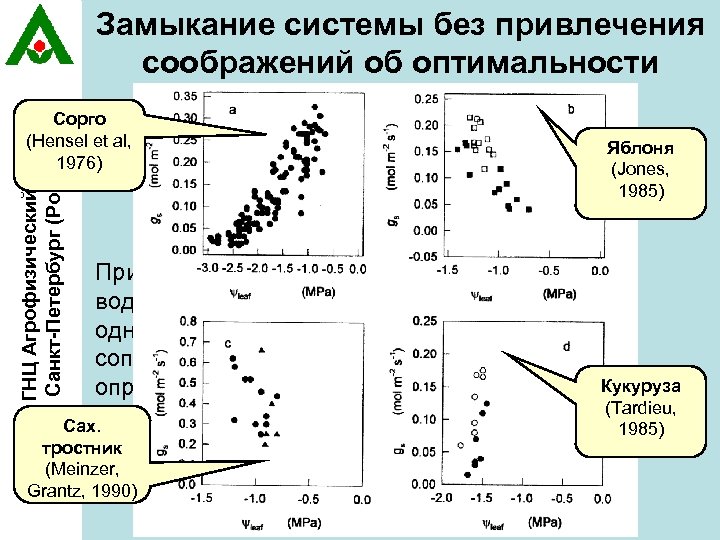
Замыкание системы без привлечения соображений об оптимальности ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Дополнительное Сорго (Hensel et al, 1976) соотношение: Яблоня (Jones, 1985) При этом система уравнений радиационного и водного балансов может быть разрешена однозначно и полученное значение устьичного сопротивления используется в уравнениях для Кукуруза определения интенсивности первичной (Tardieu, ассимиляции Сах. 1985) тростник (Meinzer, Grantz, 1990)
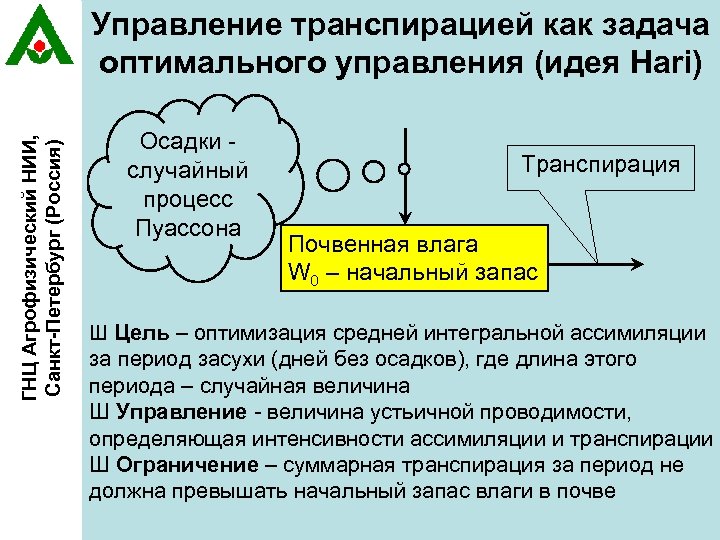
ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Управление транспирацией как задача оптимального управления (идея Hari) Осадки случайный процесс Пуассона Транспирация Почвенная влага W 0 – начальный запас Ш Цель – оптимизация средней интегральной ассимиляции за период засухи (дней без осадков), где длина этого периода – случайная величина Ш Управление - величина устьичной проводимости, определяющая интенсивности ассимиляции и транспирации Ш Ограничение – суммарная транспирация за период не должна превышать начальный запас влаги в почве

ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Описательная формализация модели 1. Под управлением понимается интенсивность транспирации. При этом устьичное сопротивление может быть однозначно определено из уравнения радиационного баланса 2. Возможная величина транспирации (ограничения на управление) не может превышать некой предельной величины, вычисляемой из уравнений радиационного или водного баланса в растении 3. Единственная динамическая переменная модели – влажность почвы. Ее динамика однозначно определяется управлением (транспирацией) 4. Цель управления – максимизация средней интегральной ассимиляции (фотосинтеза) в течение эффективного засушливого периода
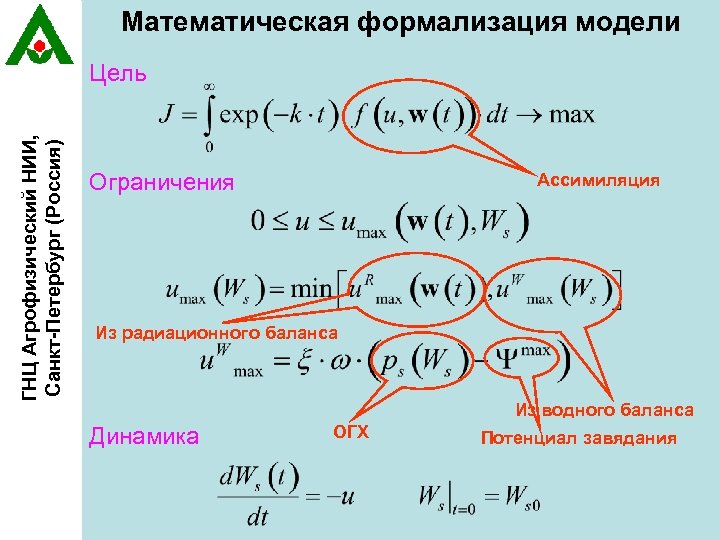
Математическая формализация модели ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Цель Ограничения Ассимиляция Из радиационного баланса Из водного баланса Динамика ОГХ Потенциал завядания

ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Решение задачи оптимизации Особенность: Динамическая переменная не входит явным образом в функционал цели, а влияет на оптимальное управление только через ограничения Пример: Гипотеза:
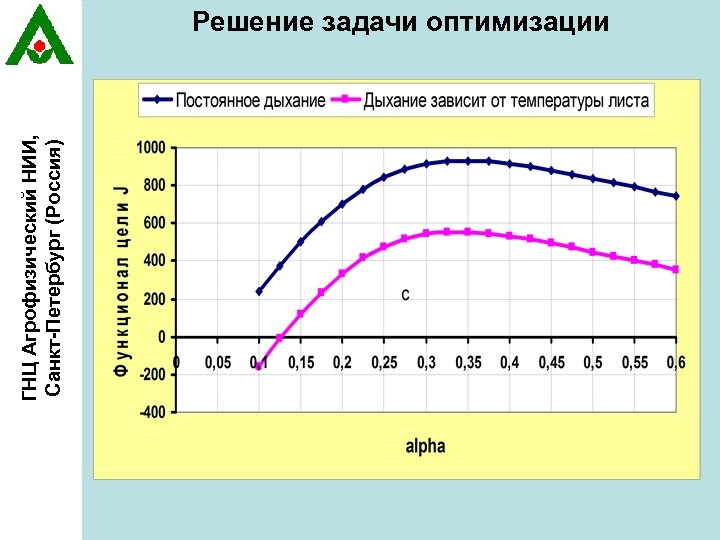
ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Решение задачи оптимизации
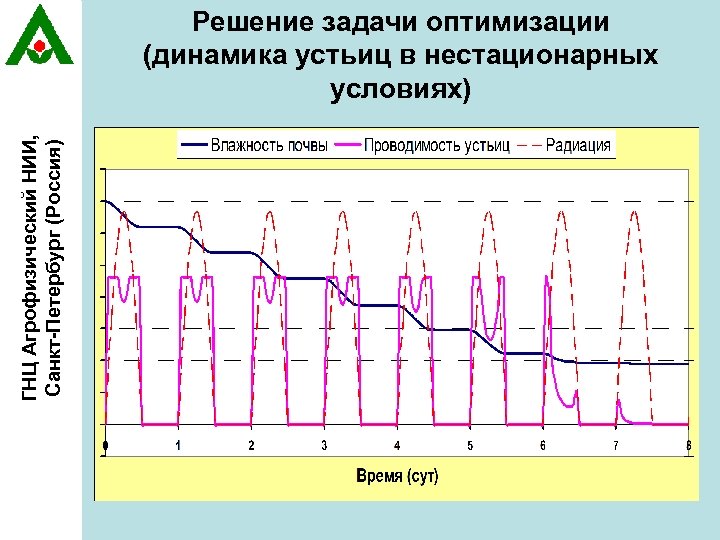
ГНЦ Агрофизический НИИ, Санкт-Петербург (Россия) Решение задачи оптимизации (динамика устьиц в нестационарных условиях)
edab0a70441bccb9d1caa7eb03d7cbd0.ppt