Gn RH neurons calcium and mathematical models James

Gn. RH neurons, calcium, and mathematical models James Sneyd, University of Auckland David Wen Duan, University of Auckland Jason Chen, University of Auckland Kiho Lee, University of Otago Allan Herbison, University of Otago Karl Iremonger, University of Otago

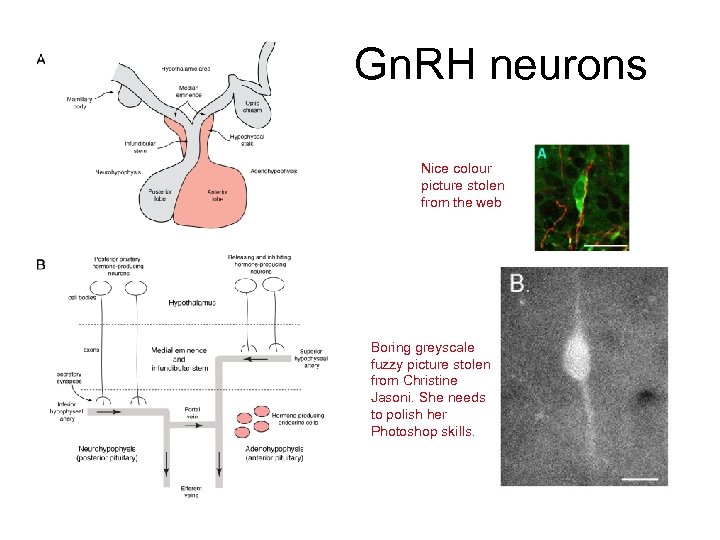Gn. RH neurons Nice colour picture stolen from the web Boring greyscale fuzzy picture stolen from Christine Jasoni. She needs to polish her Photoshop skills.

Experimental method Glow-in-the-dark mice. Glow-in-the-dark stuff P. S. This slide not approved by either Allan or Kiho. Quite the reverse, actually.

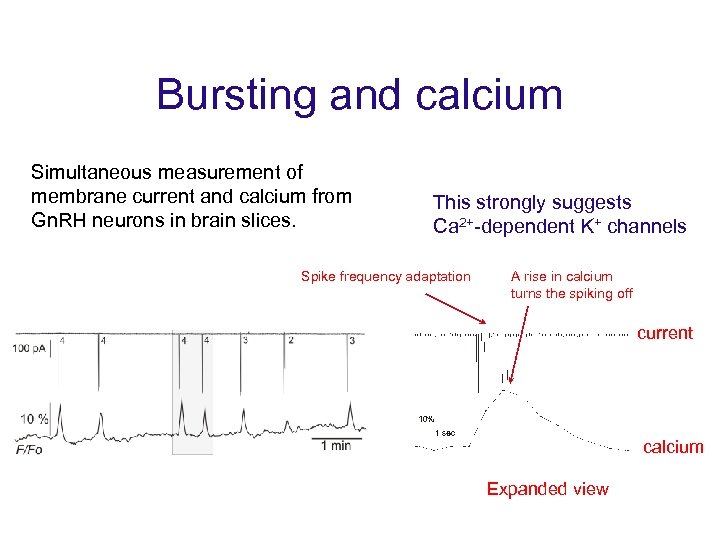Bursting and calcium Simultaneous measurement of membrane current and calcium from Gn. RH neurons in brain slices. This strongly suggests Ca 2+-dependent K+ channels Spike frequency adaptation A rise in calcium turns the spiking off current calcium Expanded view

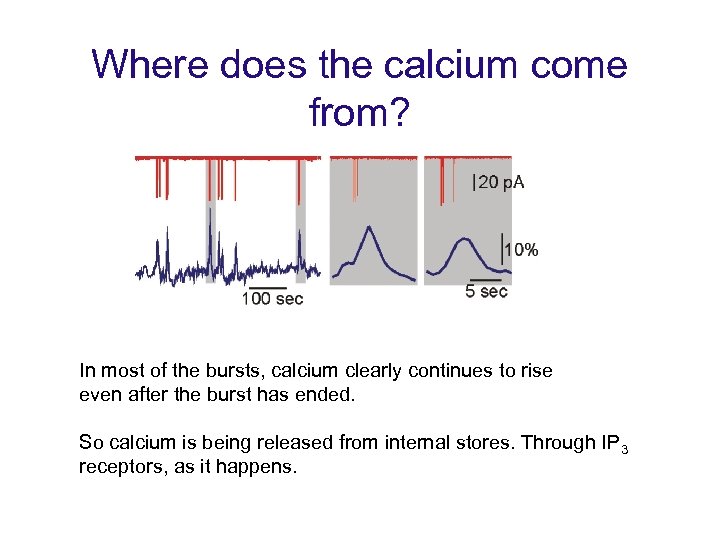Where does the calcium come from? In most of the bursts, calcium clearly continues to rise even after the burst has ended. So calcium is being released from internal stores. Through IP 3 receptors, as it happens.

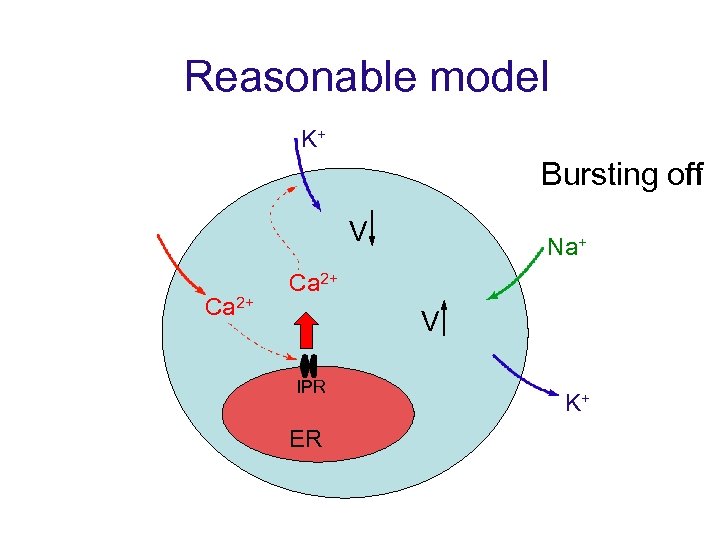Reasonable model K+ Bursting on off V Ca 2+ Na+ Ca 2+ V IPR ER K+

Problems 1. It doesn’t work. 2. It doesn’t explain what happens when you block the IPR.

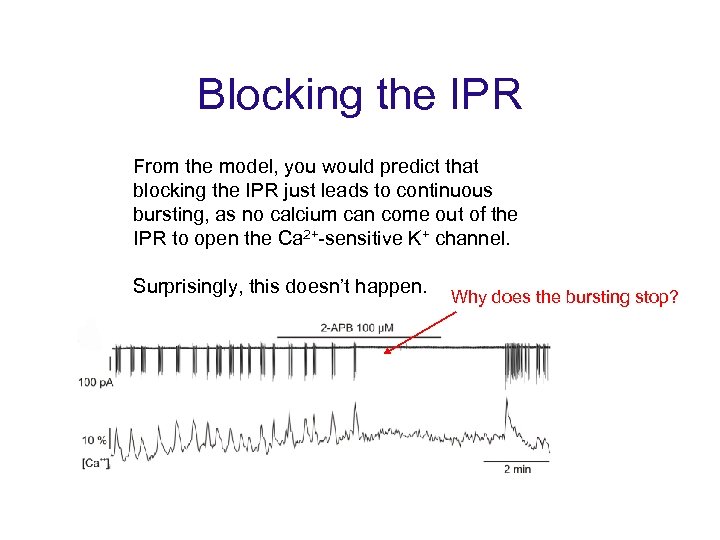Blocking the IPR From the model, you would predict that blocking the IPR just leads to continuous bursting, as no calcium can come out of the IPR to open the Ca 2+-sensitive K+ channel. Surprisingly, this doesn’t happen. Why does the bursting stop?

What else doesn’t work? What stops the bursting here?

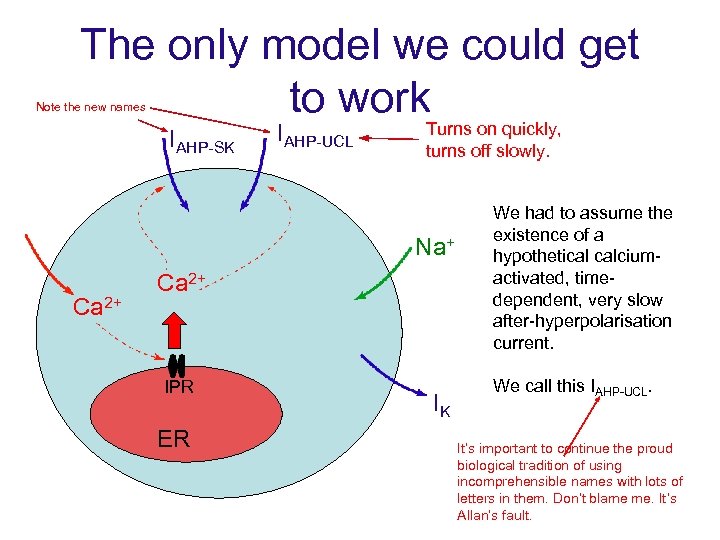The only model we could get to work Note the new names IAHP-SK IAHP-UCL Turns on quickly, turns off slowly. Na+ Ca 2+ IPR ER IK We had to assume the existence of a hypothetical calciumactivated, timedependent, very slow after-hyperpolarisation current. We call this IAHP-UCL. It’s important to continue the proud biological tradition of using incomprehensible names with lots of letters in them. Don’t blame me. It’s Allan’s fault.

According to this hypothesis Ca 2+ activates IAHP-UCL channel. Ca 2+ activates IAHP-SK channel. Switches burst off. IAHP-UCL channel prevents bursting.

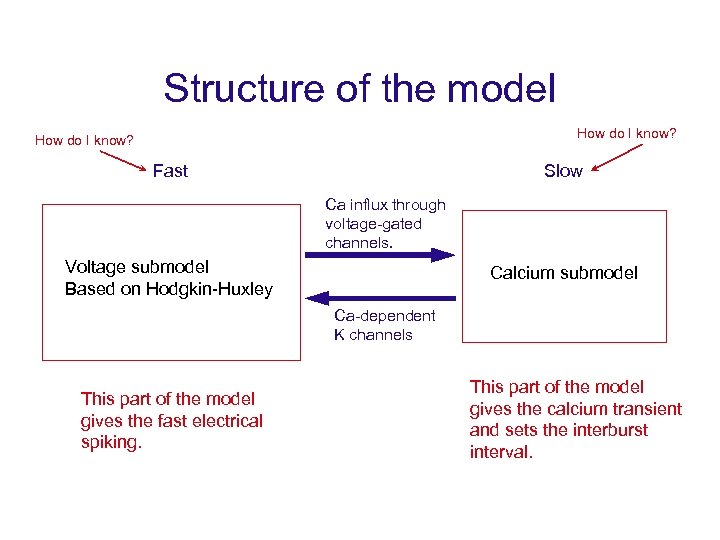Structure of the model How do I know? Fast Slow Ca influx through voltage-gated channels. Voltage submodel Based on Hodgkin-Huxley Calcium submodel Ca-dependent K channels This part of the model gives the fast electrical spiking. This part of the model gives the calcium transient and sets the interburst interval.

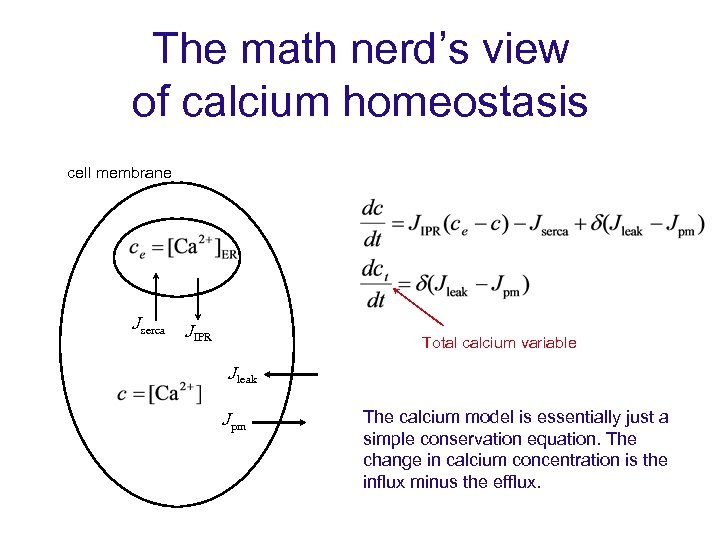The math nerd’s view of calcium homeostasis cell membrane Jserca JIPR Total calcium variable Jleak Jpm The calcium model is essentially just a simple conservation equation. The change in calcium concentration is the influx minus the efflux.

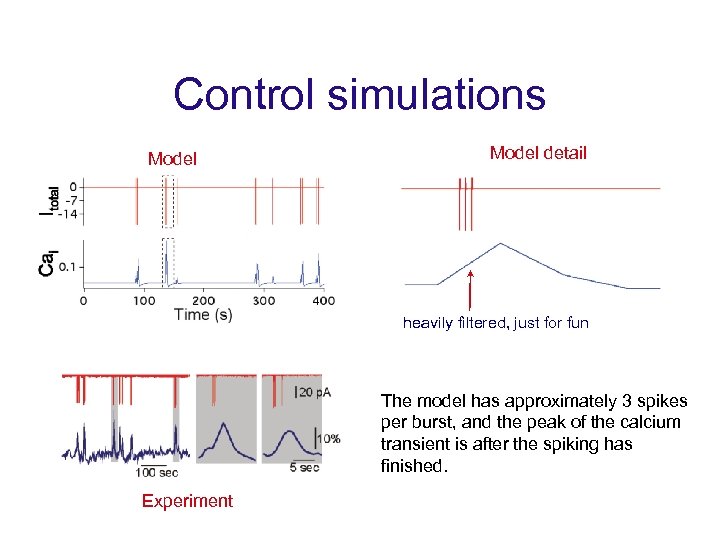Control simulations Model detail heavily filtered, just for fun The model has approximately 3 spikes per burst, and the peak of the calcium transient is after the spiking has finished. Experiment

The hypothetical channel Remember that the model assumed the existence of a really slow, calcium-dependent, time-dependent, afterhyperpolarisation current, which we called IAHP-UCL. Well, is it really there? After all, a model prediction is no use if you can’t test it.

Cue Allan and Kiho … Perforated patch, voltage-clamp traces, showing the evoked IAHP and its modulation by apamin and UCL 2077. To this day, I’m not entirely sure where Allan got the idea to use UCL 2077. I have a vague notion that it was known to block IAHP in hippocampal pyramidal cells, but please don’t ask me about this.

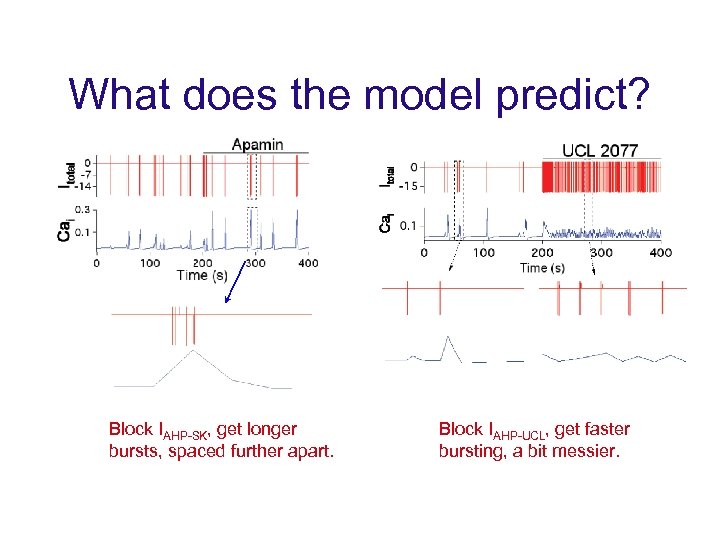What does the model predict? Block IAHP-SK, get longer bursts, spaced further apart. Block IAHP-UCL, get faster bursting, a bit messier.

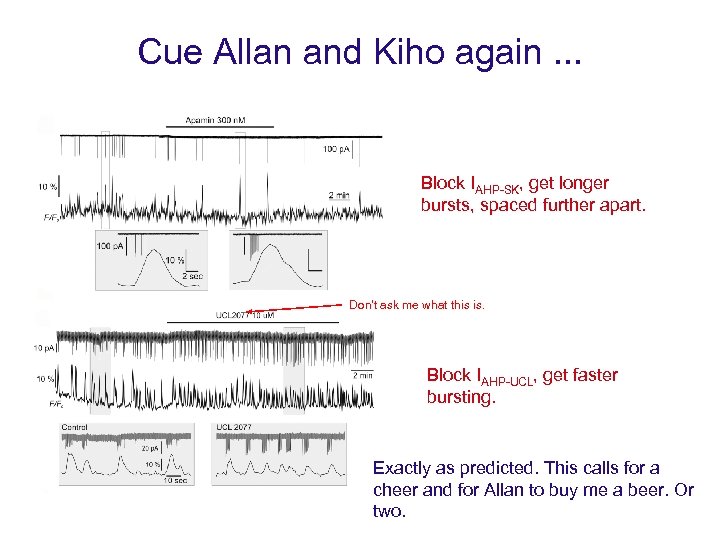Cue Allan and Kiho again. . . Block IAHP-SK, get longer bursts, spaced further apart. Don’t ask me what this is. Block IAHP-UCL, get faster bursting. Exactly as predicted. This calls for a cheer and for Allan to buy me a beer. Or two.

And so… • There are two Ca 2+-sensitive K+ channels that modulate the bursting. • One is sensitive to apamin, and regulates the end of the burst, and spike frequency adaptation. • The other is slower and time-dependent, and regulates the interburst period. • In this case, the mathematical model helped show what things to look for, and to provide a reasonable explanation for the entire range of experimental data.

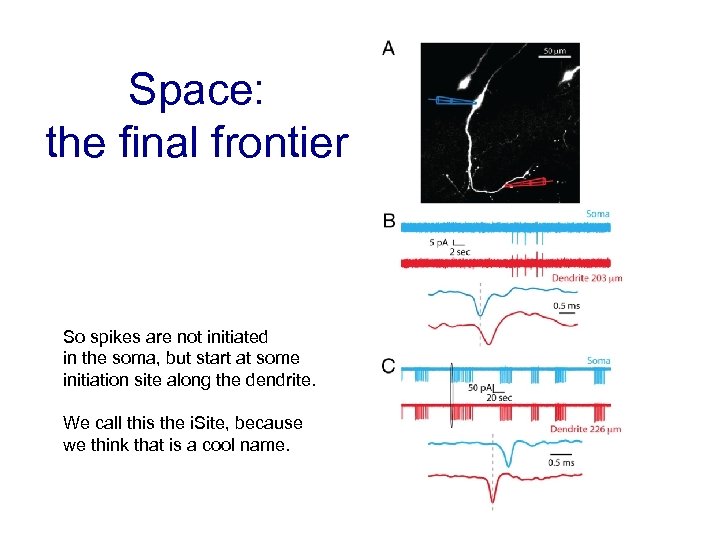Space: the final frontier So spikes are not initiated in the soma, but start at some initiation site along the dendrite. We call this the i. Site, because we think that is a cool name.

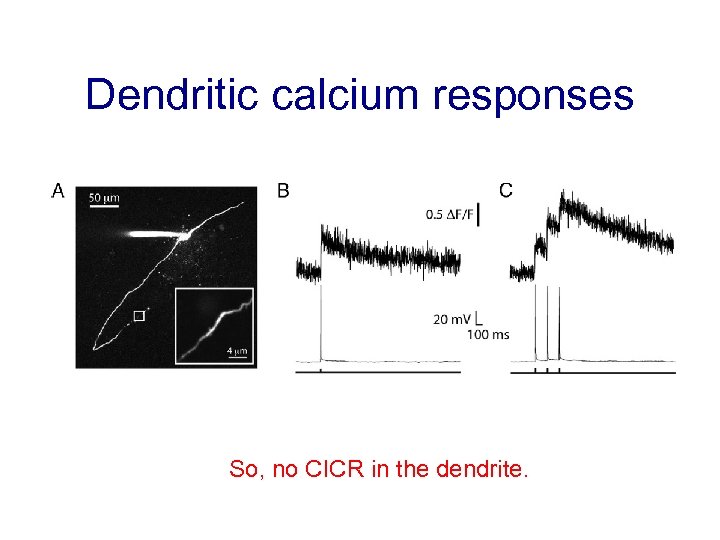Dendritic calcium responses So, no CICR in the dendrite.

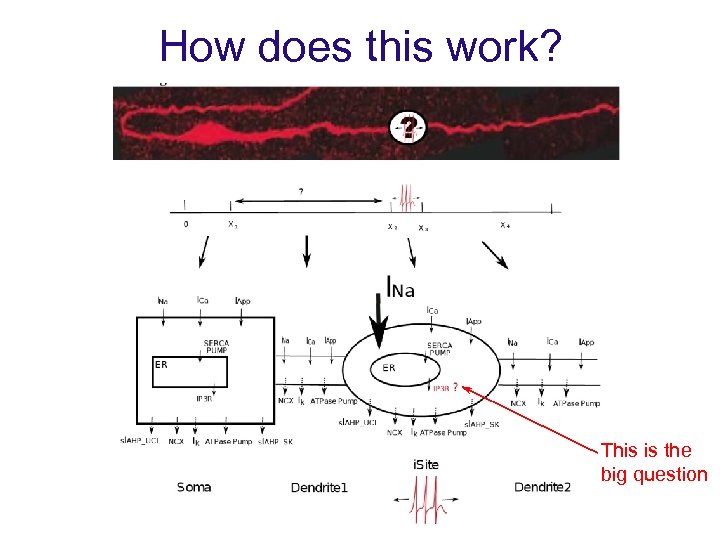How does this work? This is the big question

Our initial thoughts • IP 3 receptors control when the burst stops (via CICR and activation of Ca 2+-dependent K+ channels). • So, we said that IP 3 receptors had to be present in the i. Site. • Allan disagreed. • He told us to go back and check the model. • We told him to go back and look for IP 3 receptors.

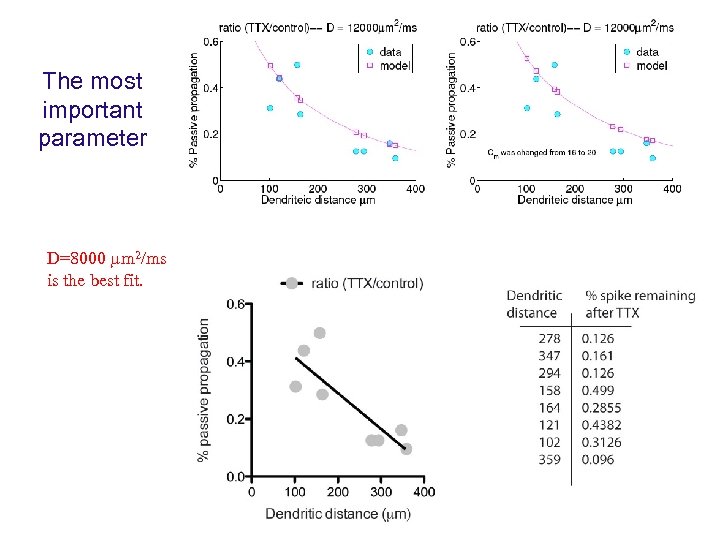The most important parameter D=8000 mm 2/ms is the best fit.

Close electrical coupling This is a pretty large value for the electrical diffusive coupling and it means that the soma and the i. Site are practically identical electrically.

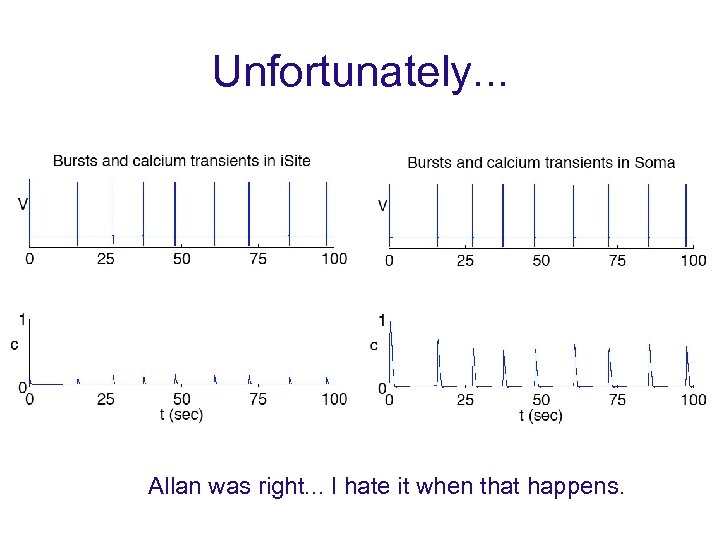Unfortunately. . . Allan was right. . . I hate it when that happens.

Lots of questions remain • Our model requires a very particular kind of IAHP-UCL, with specified dynamics and calcium-dependence. This needs to be tested. If I was forced to bet, I’d say that the model is (very) unlikely to have captured the behaviour of that channel completely. • We predict that blockage of the IPR, with no additional effect on calcium pumps won’t do anything very interesting. Is this true? Good question. • The bursting is not actually a limit cycle, as far as we know. It's driven by stochastic inputs from outside. We've done this model, as it happens, and very little changes, so we just show the deterministic results, as they are easier to show. • What on earth is the i. Site doing way out there? Are there multiple i. Sites? Why have an i. Site at all? Weird.

Reminder. . . excitable systems defines the slow manifold Because e << 1 the solution jumps between branches of the slow manifold (approximately). I have to say approximately because otherwise Martin and Vivien will tell me off. That’s because they are real mathematicians and I’m not.

Reminder. . . bursting oscillations Pretend c is constant, and sketch the bifurcation diagram of the fast system, as a function of c. A fast system (v and w) modulated by a slow variable, c. The actual solution now jumps between the branches of the fast subsystem. Transitions at the SN and HC bifurcations.

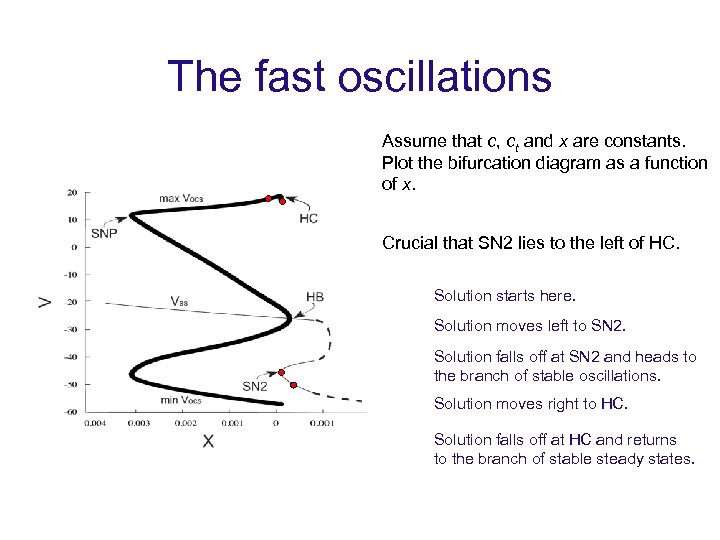The fast oscillations Assume that c, ct and x are constants. Plot the bifurcation diagram as a function of x. Crucial that SN 2 lies to the left of HC. Solution starts here. Solution moves left to SN 2. Solution falls off at SN 2 and heads to the branch of stable oscillations. Solution moves right to HC. Solution falls off at HC and returns to the branch of stable steady states.

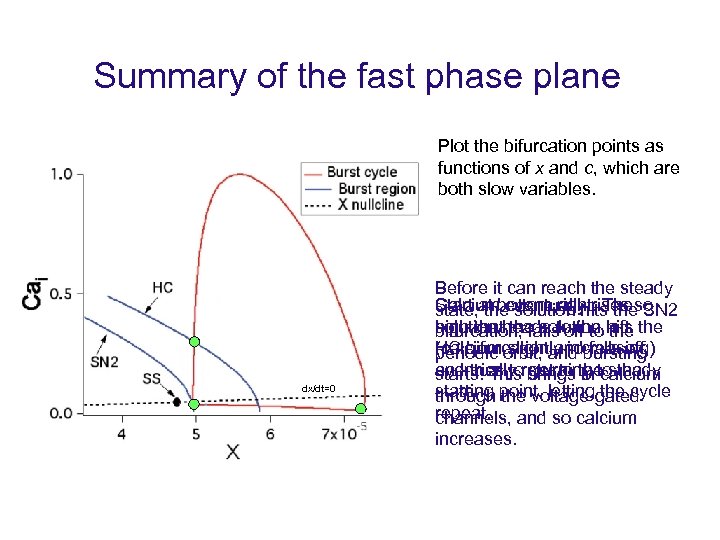Summary of the fast phase plane Plot the bifurcation points as functions of x and c, which are both slow variables. dx/dt=0 Before it can reach the steady Calcium eventually rises SN 2 Start at bottom right. Theso state, the solution hits the high that the solution left solution heads to the hits the bifurcation, falls off to the HC bifurcation and falls off, (calcium orbit, and bursting periodic slightly increasing) eventually brings thecalcium and tries toreturning tosteady starts. This get to in the starting the voltage-gated state. point, letting the cycle through repeat. and so calcium channels, increases.

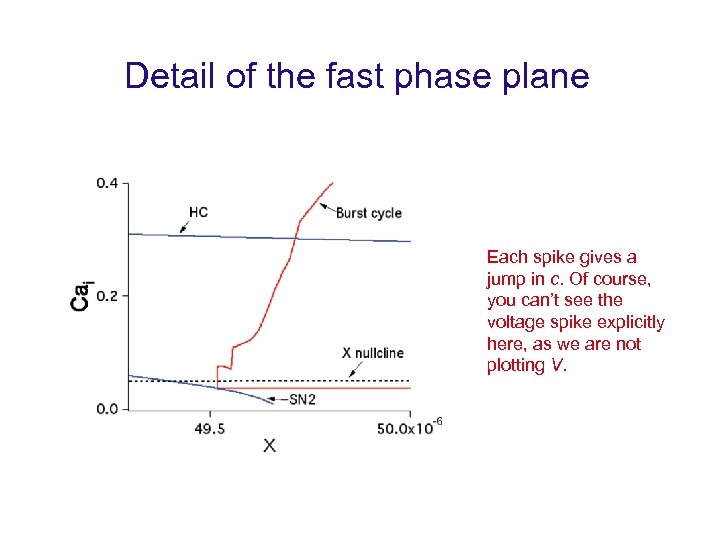Detail of the fast phase plane Each spike gives a jump in c. Of course, you can’t see the voltage spike explicitly here, as we are not plotting V.

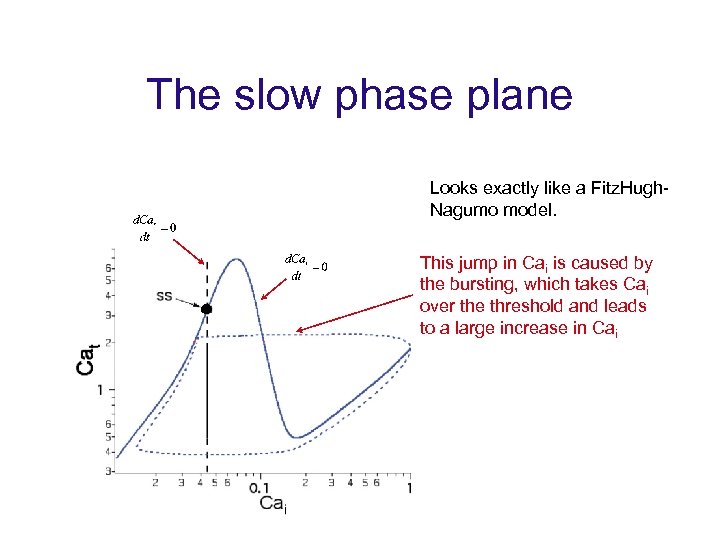The slow phase plane Looks exactly like a Fitz. Hugh. Nagumo model. This jump in Cai is caused by the bursting, which takes Cai over the threshold and leads to a large increase in Cai

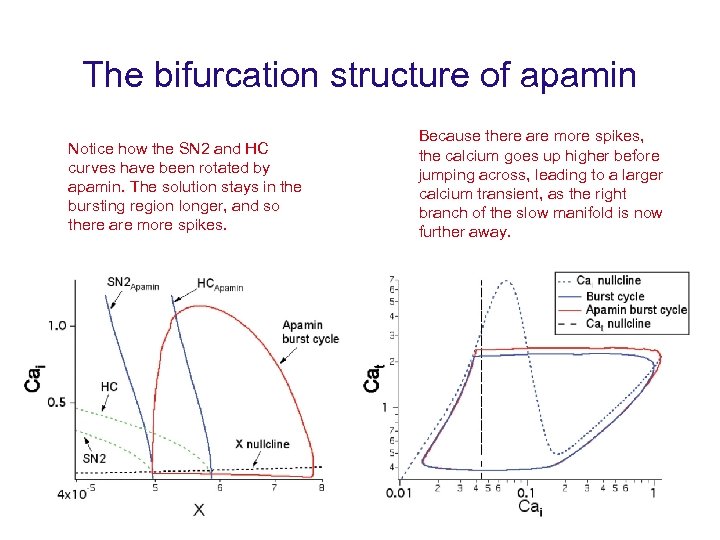The bifurcation structure of apamin Notice how the SN 2 and HC curves have been rotated by apamin. The solution stays in the bursting region longer, and so there are more spikes. Because there are more spikes, the calcium goes up higher before jumping across, leading to a larger calcium transient, as the right branch of the slow manifold is now further away.

One can continue. . . to play this game for all the pharmacological perturbations, but there are no real surprises.

The End Thanks to: