Глухівський національний педагогічний університет імені Олександра Довженка

Глухівський національний педагогічний університет імені Олександра Довженка Презентація на тему: «ПАРАЛЕЛЬНЕ ПЕРЕНЕСЕННЯ» Робота студентки 13 -М групи Сагайдачна Ю. М. Викладач Заїка О. В. 2014

Означення Паралельне перенесення — окремий випадок руху, при якому всі точки простору пересуваються в одному і тому самому напрямку на одну і ту саму відстань. Інакше, якщо М початкове, а N зміщене положення точки, тоді вектор MN один і той самий для всіх пар точок, що відповідають одна одній в даному перетворенні. На площині паралельне перенесення виражається аналітично в прямокутній системі координат (х; у) за допомогою (х; у) (х+а; у+b), де вектор MN = (a, b)

Теорема 1 Образом прямої в паралельному перенесенні є пряма. Теорема 2 Образом півпрямої в паралельному перенесенні є співнапрямлена з нею півпряма. Теорема 3 Паралельне перенесення є рухом. Теорема 4 Паралельне перенесення площини одночасно визначається завданням однієї пари відповідних точок. Означення 1 Дві півпрямі називаються співнапрямленими, якщо вони збігаються при деякому паралельному перенесенні. Означення 2 Дві півпрямі називаються протилежно напрямленими, якщо кожна з них однаково напрямлена з півпрямою, що довільною до другої.

Властивості 1. На площині в паралельному перенесення коли вектор а не дорівнює нуль вектору немає незмінних точок. 2. Незмінними прямими площини у паралельному перенесенні вектору а є всі прямі, паралельні вектору а. 3. Якщо точка С лежить між точками А і В, то образ С´ точки С лежить між образами А´ і В´ точок А і В у будьякому паралельному перенесенні. 4. Упорядкованість точок прямої є інваріантом паралельного перенесення площини. 5. Відповідні фігури в паралельному перенесенні мають однакову орієнтацію.

Інваріанти 1. Колінеарність точок. 2. Упорядкованість точок прямої. 3. Медіана, висота, бісектриса трикутника відображається відповідно на медіану, висоту, бісектрису образу трикутника. 4. Точка перетину медіан, висот, бісектрис переходить відповідно в точку перетину медіан, висот, бісектрис. 5. Відповідні фігури в паралельному перенесенні мають однакову орієнтацію. 6. Зберігається рівність фігур.

Паралельне перенесення в координатах Виберемо прямокутну систему координат ( О, I, j) на площині, в якій визначене паралельне перенесення вектором а. Якщо А (х; у) і А´ (х´; у´) є парою відповідних точок, то АА´ = а. Нехай вектор а в ( О, I, j) має координати х₀ і у₀. Знайдемо вираження координат х‘, у‘ точки образу через координати х, у її прообразу. Вектор АА´ має координати х´-х і у´-у. Але АА´ = а тому х´-х =х₀, у´-у=у₀. Отже, координати х´, у´ образу виражається через координати х, у прообразу в паралельному перенесенні на вектор а(х; у) формулами х´ =х + х₀ у´= у+ у₀

Група всіх паралельних перенесень площини Розглянемо нескінчену множину Р= а₀, а₁, а₂…. . а. . Всіх паралельних перенесень площини, тобто множині Р належать усі можливі в площині вектори. Властивості: 1. Композиція двох будь-яких паралельних перенесень а₀ і а₁ множини Р є також паралельним перенесенням а₂, що належить множині Р. 2. Композиція паралельних перенесень множини Р асоціативна. 3. Паралельне перенесення на вектор а=0 залишає незмінними всі точки площини. 4. Перетворення, обернене до будь-якого паралельного перенесення а₁ з множини Р, є також паралельним перенесенням на вектор, протилежний вектору а₁.

Теорема 5 Множина Р всіх паралельних перенесень площини є групою. Теорема 6 Композиція двох осьових симетрій з паралельними осями є паралельним перенесенням. Теорема 7 Композиція повороту навколо точки і паралельного перенесення є поворотом навколо точки. Теорема 8 Композиція двох поворотів навколо різних центрів є поворотом або паралельним перенесенням.

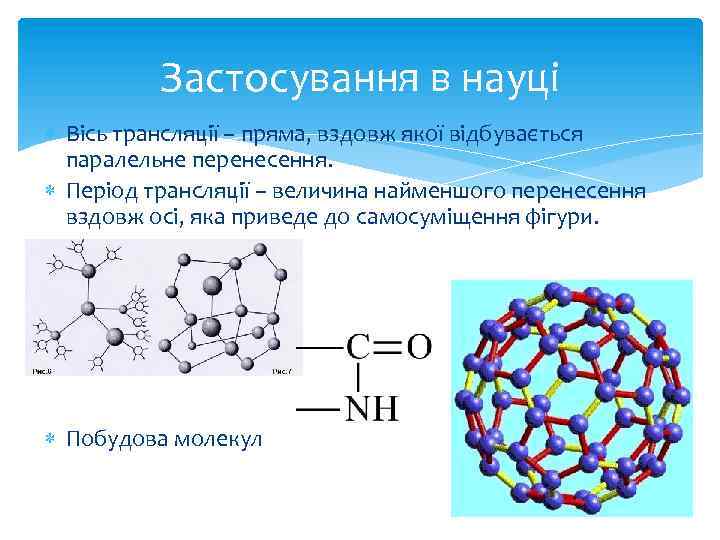Застосування в науці Вісь трансляції – пряма, вздовж якої відбувається паралельне перенесення. Період трансляції – величина найменшого перенесення вздовж осі, яка приведе до самосуміщення фігури. Побудова молекул

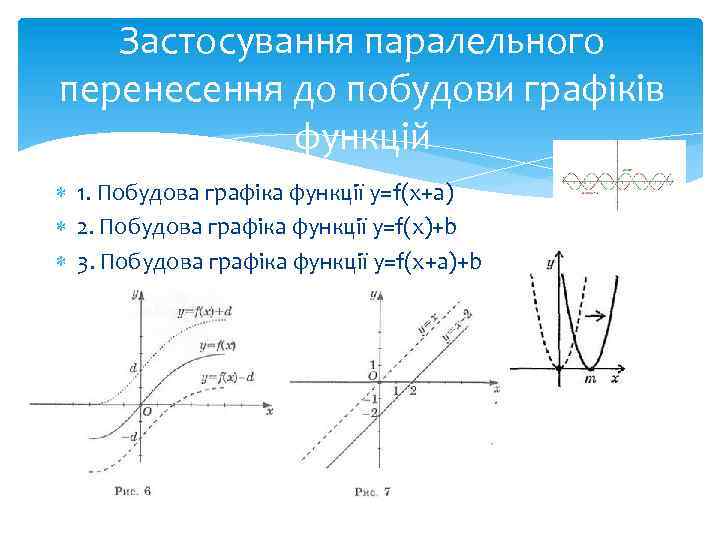Застосування паралельного перенесення до побудови графіків функцій 1. Побудова графіка функції у=f(x+a) 2. Побудова графіка функції y=f(x)+b 3. Побудова графіка функції y=f(x+a)+b

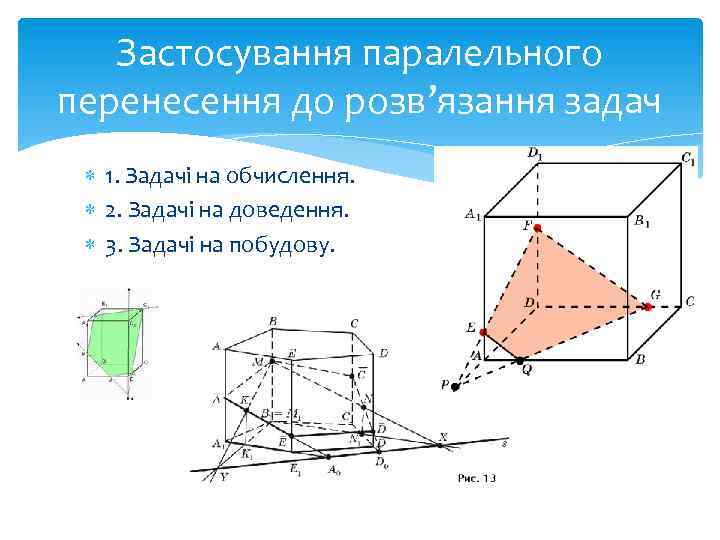Застосування паралельного перенесення до розв’язання задач 1. Задачі на обчислення. 2. Задачі на доведення. 3. Задачі на побудову.

Використані джерела Навчальний посібник «Геометричні перетворення площини» В. Н. Боровик Підручник з геометрії http: //subject. com. ua/dovidnik/geometr/38. html