Энергия и время Ольчак Lekcja_05_2015_11.ppt
- Количество слайдов: 11

Глобальный проект «Физика» Лекция 05 Энергия и время Лектор: Доцент НИЯУ МИФИ, к. ф. -м. н. , Ольчак Андрей Станиславович

Энергия и однородность свойств времени На прошлом занятии, исходя из соображений однородности свойств пространства и времени в инерциальных системах отсчета, мы установили, что функцию Лагранжа L для любой системы взаимодействующих между собой тел (группы материальных точек, находящихся возможно еще и под действием внешних потенциальных сил) можно представить в виде суммы L = T - U = Σmi. Vi 2/2 - U(r 1, r 2, …, ri, . . . ) = Σmiq'i 2/2 - U(q). где T - кинетическая энергия системы, а U(q) - ее суммарная потенциальная энергия, зависящая от координат всех тел системы. Попробуем теперь раскрыть физический смысл понятий кинетической и потенциальной энергий, входящих в эту функцию. Для этого обратимся еще раз к свойству однородности времени в инерциальных системах отсчета. С точки зрения метематической, однородность времени означает отсутствие прямой зависимости L от времени (т. е. частная производная L/ t, а также и полная производная d. L/dt от нее по времени должны равняться нулю).

Энергия и однородность свойств времени С точки зрения метематической, однородность времени означает отсутствие прямой зависимости L от времени (т. е. частная производная L/ t, а также и полная производная d. L/dt от нее по времени должны равняться нулю). Выпишем выражение для полной производной: d. L//dt = L/ t + Σ( L/ qi)(dqi/dt) + Σ ( L/ qi')(dqi'/dt) => = 0 + ( L/ qi)dqi' + ( L/ qi')qi'' Для компактности записи здесь и в дальнейшем будем опускать знак суммирования Σ, если один и тот же индекс (в нашем случае - i) встречается в произведении дважды. Будем считать, что это автоматически означает суммирование по нему. В соответствии с уравнениями Лагранжа L/ qi = d( L/ q'i)/dt сделаем замену и затем несколько простых преобразований: d. L/dt= qi' d( L/ q'i)/dt + ( L/ qi')dqi'/dt = d(q'i L/ q'i)/dt => => d(q'i L/ q'i - L)/dt =0 => q'i L/ q'i - L = E = Const (!!!)

Энергия и однородность свойств времени Получается, что в силу однородности свойств времени (!) некоторая величина = q'i L/ q'i E - L в процессе движения системы должна оставаться строго постоянной. Подставляя в E функцию Лагранжа в виде L = T - U = Σmiq'i 2/2 - U(q), находим: E = q'i L/ q'i - L = Σmiq'i 2 - Σmiq'i 2/2 + U = T + U = Const (!) Сохраняющуюся величину E = T + U , равную сумме кинетической и потенциальной энергии, естественно назвать полной энергией системы: E = T + U = Σmiq'i 2/2 + U(q) = Const! Напомним ограничение на возможность использования уравнений Лагранжа, и как следствие - на применимость закона сохранения энергии: учитываются только потенциальные силы, неконсервативные силы - сила трения, например - не учитываются.

Закон сохранения энергии Заметим еще раз: в обобщенной теоретической механике сперва появляются обозначения для кинетической T и потенциальной U энергий как слагаемых функции Лагранжа (причем без особого пояснения их физического смысла), а потом только возникает определение силы - как градиента от потенциальной энергии, взятого со знаком минус. Мы знаем также, что отнюдь не любую силу можно представить в таком виде. Силы трения, например, не являются потенциальными. С другой стороны, понятие энергии и закон ее сохранения в курсе общей физики обычно вводятся без связи с фактом однородности свойств времени, но в связи с понятием механической работы, совершаемой действующими на объекты силами, что позволяет яснее понять физический смысл этих понятий. Дадим теперь определение понятиям работы и энергии.

Работа. Мощность. Введем (или напомним) основные определения, связанные с понятиями работы и мощности сил в механике. • Элементарная работа силы. d. A = (F, dr) = F dr cosα • Работа силы на участке траектории 2 от точки 1 до точки 2 1 A 12 = d. A = (F, dr) 1 • • Мгновенная мощность силы • Средняя мощность силы P = d. A/dt = (F, dr/dt) = (F, v) = Fv cosα Определение работы по известной зависимости мощности от времени

Связь работы и энергии. Элементарная работа силы d. A = (F, dr) Возьмем уравнение второго закона Ньютона, умножим его скалярно на перемещение dr и проделаем некоторые простые преобразования, переставляя местами сомножители в скалярном произведении и меняя место операции взятия производной d. A= (F, dr) = m(dr, dv/dt) = m(dv, dr/dt) = m(dv, v) = d(mv 2/2) ВЫВОД: работа внешней силы идет на приращение (или убыль, если сила направлена против скорости) кинетической энергии системы. И наоборот: наличие кинетической энергии у тела позволяет ему совершить положительную работу против внешней силы, препятствующей его движению. Работа силы и работа против силы равны по величине и имеют противоположные знаки. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ тела -- мера способности совершить ту или иную (полезную или разрушительную) работу за счет самого факта движения тела.

Консервативные силы и потенциальная энергия • • Консервативными называются силы, работа которых не зависит от формы траектории, а зависит только от начального и конечного положений частицы. Это гравитационные силы, сила упругости, сила Кулона, сила Архимеда. СЛЕДСТВИЕ: Для консервативных сил можно ввести понятие потенциальной энергии, зависящей исключительно от координат точки в поле консервативной силы. Работа консервативной силы равна разности потенциальных энергий объекта в начальной и конечной точках траектории: А 12 = U 1 - U 2. Физический смысл имеет именно разность значений потенциальной энергии между разными точками. Работа консервативных сил на замкнутой траектории равна нулю. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ - мера способности тела совершить работу за счет взаимодействия с другими телами.
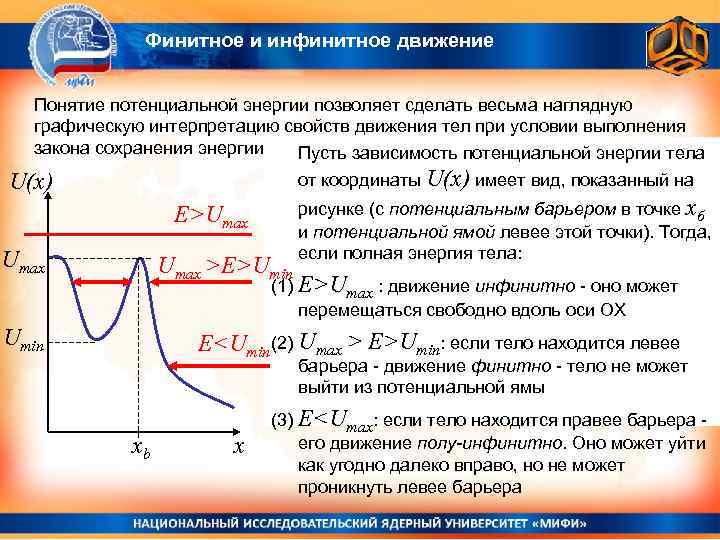
Финитное и инфинитное движение Понятие потенциальной энергии позволяет сделать весьма наглядную графическую интерпретацию свойств движения тел при условии выполнения закона сохранения энергии. Пусть зависимость потенциальной энергии тела от координаты U(x) имеет вид, показанный на U(x) E>Umax >E>Umin рисунке (с потенциальным барьером в точке хб и потенциальной ямой левее этой точки). Тогда, если полная энергия тела: (1) E>Umax : движение инфинитно - оно может перемещаться свободно вдоль оси ОХ Umin E<Umin (2) Umax > E>Umin: если тело находится левее барьера - движение финитно - тело не может выйти из потенциальной ямы xb x (3) E<Umax: если тело находится правее барьера его движение полу-инфинитно. Оно может уйти как угодно далеко вправо, но не может проникнуть левее барьера

Неконсервативные силы. Баланс энергии Работа неконсервативных сил (сила трения, например) зависит от формы траектории. В частности, для силы трения она всегда отрицательна, даже на замкнутой траектории. Для неконсервативных сил нельзя ввести понятие потенциальной энергии. Уравнение баланса энергии - бухгалтерия природы. Если Е 1 = T 1 + U 1 - начальная энергия системы, а Е 2 = T 2 + U 2 - ее конечная энергия, то Е 1 - Е 2 = А’ 12 = -А 12 Здесь А 12 - работа внешних неконсервативных сил; А’ 12 = - А 12 - работа, совершенная телами системы против неконсервативных сил. В частности, работа против силы трения всегда положительна и приводит к уменьшению полной механической энергии системы. Эта энергия не исчезает, но преобразуется в другую форму - тепловую. При этом любая энергия (как и работа) в системе СИ измеряется в Джоулях. 1 Дж = 1 кг • м 2/с2.

Энергия - валюта природы Таким образом, энергией в физике называют меру способности объекта совершить ту или иную (полезную или разрушительную) работу. Чем больше энергия - тем большую работу способен объект ей обладающий совершить. Определение, вполне соответствующее пониманию смысла слова «энергия» в обычном (общеупотребительном) языке. Энергия бывает не только механической, но также и электрической, тепловой, атомной и т. д. и эти виды энергии способны преобразовываться друг в друга. Энергия чем-то напоминает деньги природы. Как доллары в любом обменном пункте можно конвертировать в евро, а потом обратно, но уже с некоторой потерей, так и энергию механическую (например, падающей воды на электростанции) можно преобразовать, например, в электрическую, а потом опять в механическую, но уже с некоторыми неизбежными потерями на нагревание окружающей среды. И, как и доллары, энергию можно измерить и сосчитать количественно точно, как это и делается в физике.
Энергия и время Ольчак Lekcja_05_2015_11.ppt