Глобальный проект Физика Часть 02 На подходе к

Глобальный проект «Физика» Часть 02 На подходе к настоящей Физике - физика Аристотеля и Великие Догадки Ньютона Лектор: доцент НИЯУ МИФИ, к. ф. -м. н. , Ольчак Андрей Станиславович

Глобальный проект «Физика» Физику можно рассматривать как глобальный проект, имеющий своей задачей количественное и обладающее расчетно-предсказательной силой описание всего окружающего мира. Многое на свете не поддается такому описанию (некоторые физики верят, что пока не поддается), но многое поддается. Углубляться в этот проект мы будем естественным путем шаг за шагом, от самых простых случаев переходя постепенно к более сложным. И начнем мы с описания простого движения материальных объектов, которое мы можем непосредственно наблюдать

Механика Аристотеля Исторически первая попытка как-то решить эту задачу была предпринята Аристотелем и его последователями. Правда, Аристотель не знал дифференциальных уравнений и вообще практически не употреблял математики, но некоторые общие принципы он сформулировал. Аристотель исходил из наблюдений и житейского опыта, который любому из нас, также, как и Аристотелю, подсказывает, что для того, чтобы что-либо сдвинуть с места - надо приложить усилие. Правда, наблюдения указывают на то, что некоторые движения происходят и без видимо приложенных усилий - например, камни катятся с горы а дым от костра поднимается вверх как-бы сами-собой. Аристотель еще хорошо знал про звезды, описывающие простые круговые (циклические) траектории на небесном своде, и планеты, чье движение по небесному своду сложнее, но тоже складывается из накладывающихся друг на друга эпициклов.

Механика Аристотеля В вольной трактовке, основы механики по Аристотелю можно сформулировать примерно так. 1. Движения бывают естественными и вынужденными. 2. К естественным движениям, не требующим дополнительного прояснения причин, относятся: - движение тяжелых тел вниз (например, камню естественно скатиться с горы или упасть с обрыва) - движение легких тел вверх (например, дым от костра, поднимающийся к небу) - движение небесных ( «божественных» ) тел по окружностям и эпициклам 3. Все остальные виды движения могут быть только вынужденными и требуют приложения внешних сил (импетусов - по Аристотелю). Для некоторых случаев приложение импетуса должно быть постоянным - как при ходьбе или толкании повозки. Для других - импетус может быть приложен однократно. Он действует какое-то время, а потом тело останавливается или переходит на естественное движение (например, камень, брошенный вверх, по истечении действия приложенного импетуса естественно падает вниз).

Механика Аристотеля - это еще не физика, хотя именно труды Аристотеля ввели в научный обиход этот термин. Аристотель не использовал математику, но сформулированные им принципы достаточно логичны (с точки зрения житейского опыта и здравого смысла) и даже обладают некоторой количественной предсказательной силой. Когда в 15 -16 веках в европейских войнах стала применяться артиллерия - встала задача: как попасть из пушки в нужный объект, скрытый за крепостной стеной? Решали ее так. Проводили опытную стрельбу в чистом поле - замеряли, на каком расстоянии L упадет снаряд. Как-бы именно настолько хватает «импетуса» порохового заряда. Далее ставили пушку перед крепостной стеной и стреляли под таким углом, чтобы импетус иссяк точно над объектом. И попадали!. . . L L

Механика Аристотеля Но ведь мы с вами учились в школе, где нам объясняли, что по законам Ньютона снаряд, пущенный из пушки, летит по параболической, а не по треугольной траектории. Должен быть «перелет» ! Или Ньютон не прав? Прав Ньютон и еще как прав! Дело в том, что снаряд испытывает сильное сопротивление воздуха, искажающее его траекторию и делающее ее похожей на треугольник (мы разберем эту задачу позднее). Именно из-за сопротивления среды нам приходится постоянно прикладывать усилия, чтобы идти, толкать повозку и т. п. Если бы не было сопротивления среды и никаких других сил воздействующих на него - тело двигалось бы с постоянной скоростью, не меняя ее ни по величине ни по направлению. Вот с этой Великой Догадки сэра Исаака Ньютона и начинается настоящая Физика!

На подступах к настоящей Физике Догадка о том, что если на тело не действуют никакие силы - оно должно либо покоиться, либо двигаться равномерно и прямолинейно была не единственной Великой Идеей сэра Исаака! Опираясь на опыты предшественников (в частности – Коперника и Галилея) и на собственные наблюдения сэр Исаак в 1670 -ые годы (а вовсе не Альберт Эйнштейн в 20 веке) сформулировал Принцип Относительности: состояние покоя, как и любое движение относительны и зависят от того, из какой системы отсчета за движением следит наблюдатель. Например, наблюдателю на берегу кажется движущейся лодка на реке, а кусты у берега кажутся неподвижными. Для наблюдателя в лодке неподвижна сама лодка, а человек на берегу вместе с кустами кажутся движущимися. Конечно, можно возразить, что берег и шаткая лодочка на зыбкой воде - это неравноценные системы отсчета. Но всегда ли такая неравноценность очевидна? А кроме того….

Вот они - Отцы-Основатели современной физики Isaac Newton 1643 - 1727 Mikołaj Kopernik 1473 - 1543 Galileo Galilei 1564 - 1642 …и про каждого можно рассказать удивительную и увлекательную историю

На подступах к настоящей Физике А кроме того - если состояние покоя и состояние равномерного прямолинейного движения в равной мере возникают при отсутствии каких либо реальных сил, действующих на тело, почему бы не считать системы отсчета, что покоятся или движутся относительно друг-друга равномерно и прямолинейно - также совершенно равноправными? Это вторая Великая Идея Ньютона, легшая в основание настоящей Физики. И опять далеко не последняя! А как-же быть с «естественными» движениями Аристотеля? Камни падают вниз явно не с постоянной скоростью, а небесные тела движутся явно не прямолинейно. Как быть с ними? А вот тут, говорит Ньютон, возможны две ситуации. 1. Солнце и звезды - все движутся по небосводу, описывая окружности, причем за одно и то же время - ровно за 1 земные сутки. Разумно предположить, что их движение «кажущееся» для наблюдателя, находящегося на поверхности вращающейся именно с этим периодом Земли (Ньютон конечно-же читал труды Галилео Галилея!)

На подступах к настоящей Физике 2. Все остальные «естественные» движения с переменной скоростью падающие с дерева яблоки, поднимающийся дым, и -(sic!) - планеты (небесные тела, описывающие на небосводе сложные траектории и с разными периодами) - на самом деле, по Ньютону, происходят под действием реальных сил. Для планет, камней, яблок и пр. - это универсальная сила притяжения, действующая между любыми телами, обладающими массой (!). Земля притягивает камни и яблоки так же, как Солнце притягивает планеты (Ньютон был знаком и с расчетами Коперника тоже). А различия характера движения объясняются разными начальными условиями и математикой (об этом позже). Еще одна гениальная догадка! И первый шаг в реализации глобального проекта Физика - объяснить самые разные явления исходя из общих первопринципов.

Глобальный проект «Физика» Физику можно рассматривать как глобальный проект, имеющий своей задачей количественное и обладающее расчетнопредсказательной силой описание всего окружающего мира. Мы начинаем с описания простого движения материальных объектов, которое мы можем непосредственно наблюдать

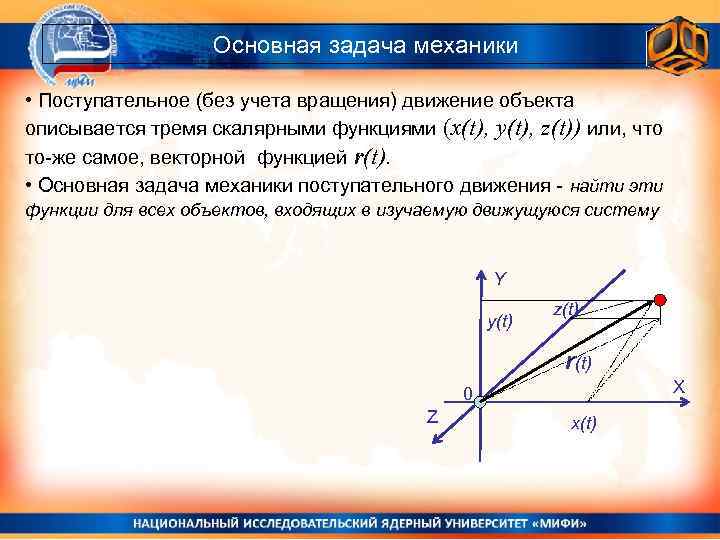
Основная задача механики • Поступательное (без учета вращения) движение объекта описывается тремя скалярными функциями (x(t), y(t), z(t)) или, что то-же самое, векторной функцией r(t). • Основная задача механики поступательного движения - найти эти функции для всех объектов, входящих в изучаемую движущуюся систему Y y(t) z(t) r(t) X 0 Z x(t)

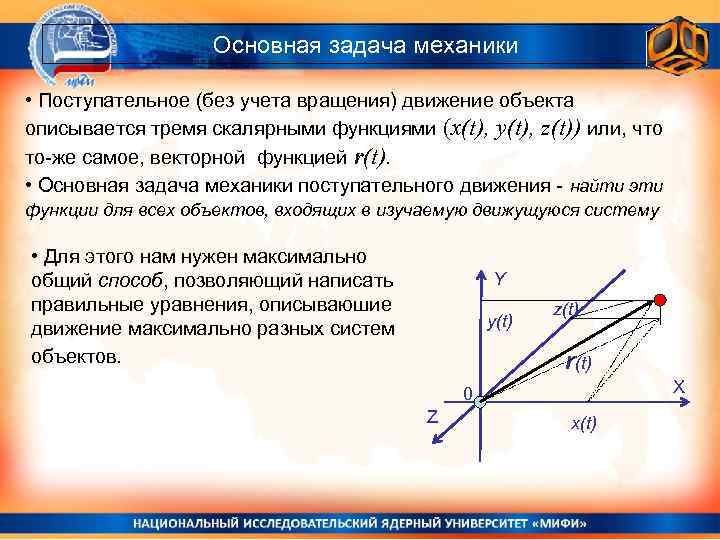
Основная задача механики • Поступательное (без учета вращения) движение объекта описывается тремя скалярными функциями (x(t), y(t), z(t)) или, что то-же самое, векторной функцией r(t). • Основная задача механики поступательного движения - найти эти функции для всех объектов, входящих в изучаемую движущуюся систему • Для этого нам нужен максимально общий способ, позволяющий написать правильные уравнения, описываюшие движение максимально разных систем объектов. Y y(t) z(t) r(t) X 0 Z x(t)

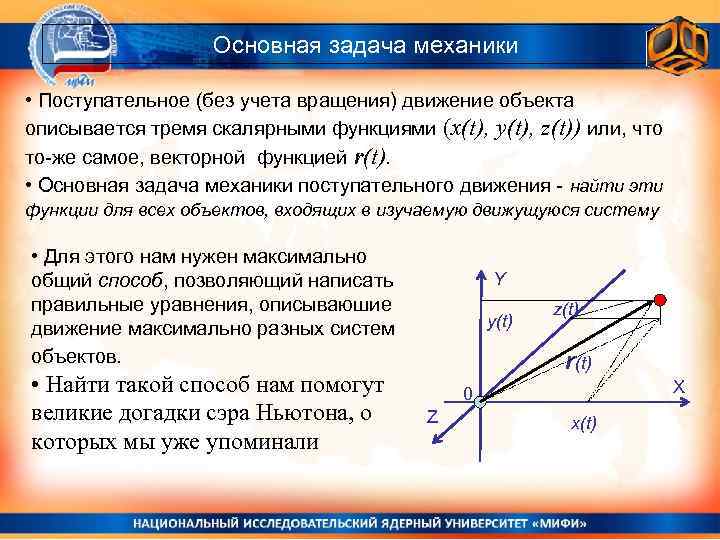
Основная задача механики • Поступательное (без учета вращения) движение объекта описывается тремя скалярными функциями (x(t), y(t), z(t)) или, что то-же самое, векторной функцией r(t). • Основная задача механики поступательного движения - найти эти функции для всех объектов, входящих в изучаемую движущуюся систему • Для этого нам нужен максимально общий способ, позволяющий написать правильные уравнения, описываюшие движение максимально разных систем объектов. • Найти такой способ нам помогут великие догадки сэра Ньютона, о которых мы уже упоминали Y y(t) z(t) r(t) X 0 Z x(t)

Основы механики Ньютона

Основы механики Ньютона • Догадка о том, что если на тело не действуют никакие силы - оно должно либо покоиться, либо двигаться равномерно и прямолинейно.

Основы механики Ньютона • Догадка о том, что если на тело не действуют никакие силы - оно должно либо покоиться, либо двигаться равномерно и прямолинейно. • Принцип Относительности: состояние покоя, как и любое движение относительны и зависят от того, из какой системы отсчета за движением следит наблюдатель.

Основы механики Ньютона • Догадка о том, что если на тело не действуют никакие силы - оно должно либо покоиться, либо двигаться равномерно и прямолинейно. • Принцип Относительности: состояние покоя, как и любое движение относительны и зависят от того, из какой системы отсчета за движением следит наблюдатель. • Следствие: если состояние покоя и состояние равномерного прямолинейного движения в равной мере возникают при отсутствии каких либо реальных сил, действующих на тело, почему бы не считать системы отсчета, что покоятся или движутся относительно друг-друга равномерно и прямолинейно - также совершенно равноправными?

Основы механики Ньютона • Догадка о том, что если на тело не действуют никакие силы - оно должно либо покоиться, либо двигаться равномерно и прямолинейно. • Принцип Относительности: состояние покоя, как и любое движение относительны и зависят от того, из какой системы отсчета за движением следит наблюдатель. • Следствие: если состояние покоя и состояние равномерного прямолинейного движения в равной мере возникают при отсутствии каких либо реальных сил, действующих на тело, почему бы не считать системы отсчета, что покоятся или движутся относительно друг-друга равномерно и прямолинейно - также совершенно равноправными? • Те системы отсчета, в которых тела, на которые не действуют никакие реальные физические силы, движутся равномерно и прямолинейно называются инерциальными

Основы механики Ньютона • Догадка о том, что если на тело не действуют никакие силы - оно должно либо покоиться, либо двигаться равномерно и прямолинейно. • Принцип Относительности: состояние покоя, как и любое движение относительны и зависят от того, из какой системы отсчета за движением следит наблюдатель. • Следствие: если состояние покоя и состояние равномерного прямолинейного движения в равной мере возникают при отсутствии каких либо реальных сил, действующих на тело, почему бы не считать системы отсчета, что покоятся или движутся относительно друг-друга равномерно и прямолинейно - также совершенно равноправными? • Те системы отсчета, в которых тела, на которые не действуют никакие реальные физические силы, движутся равномерно и прямолинейно называются инерциальными • Все инерциальные системы отсчета, что покоятся или движутся относительно друг-друга равномерно и прямолинейно - совершенно равноправны

Механика Ньютона Так что-же получается? Если в «правильной» (как минимум - не вращающейся) - инерциальной системе отсчета на тело не действуют никакие реальные силы со стороны других материальных объектов - оно будет покоиться или двигаться равномерно и прямолинейно с постоянной по величине и направлению скоростью V. Если-же силы действуют - то скорость будет меняться, и скорость изменения скорости (ускорение) будет тем больше, чем больше суммарная действующая результирующая сила. md. V/dt = md 2 r/dt 2 = ΣF = Fres

Механика Ньютона Так что-же получается? Если в «правильной» (как минимум - не вращающейся) - инерциальной системе отсчета на тело не действуют никакие реальные силы со стороны других материальных объектов - оно будет покоиться или двигаться равномерно и прямолинейно с постоянной по величине и направлению скоростью V. Если-же силы действуют - то скорость будет меняться, и скорость изменения скорости (ускорение) будет тем больше, чем больше суммарная действующая результирующая сила. md. V/dt = md 2 r/dt 2 = ΣF = Fres Это знаменитый великий Второй Закон Ньютона! Величина m - мера инертности тела, именуемая массой. Чем она больше, тем труднее изменить скорость тела одной и той же силе. Если ввести понятие вектора импульса тела P = m. V, Второй Закон Ньютона можно переписать в форме, которую предпочитал сам Ньютон: d. P/dt = Fres

Механика Ньютона Второй Закон Ньютона (ЗН_II) в форме, которую предпочитал сам Ньютон: d. P/dt = Fres или d. P = Fres dt за одно и то же (небольшое - !) время dt одна и та же сила изменит импульс любого тела на одинаковую величину. Второй закон Ньютона (ЗН-II) дополняется важнейшим третьим законом (ЗН-III), гласящим: любое действие реальных физических тел друг на друга носит характер взаимодействия. Сила, с которой первое тело действует на второе в точности равна по величине и обратна по направлению силе, действующей со стороны второго тела на первое: F 12 = -F 21

Механика Ньютона Второй Закон Ньютона (ЗН_II) в форме, которую предпочитал сам Ньютон: d. P/dt = Fres или d. P = Fres dt за одно и то же (небольшое - !) время dt одна и та же сила изменит импульс любого тела на одинаковую величину. Второй закон Ньютона (ЗН-II) дополняется важнейшим третьим законом (ЗН-III), гласящим: любое действие реальных физических тел друг на друга носит характер взаимодействия. Сила, с которой первое тело действует на второе в точности равна по величине и обратна по направлению силе, действующей со стороны второго тела на первое: F 12 = -F 21 ЗН-III позволяет записать систему уравнений ЗН-II для нескольких взаимодействующих тел, занумерованных индексом i = 1, 2, 3, . . . : d. P 1/dt = ΣFi 1 d. P 2/dt = ΣFi 2 и т. д.

Механика Ньютона Законы Ньютона - огромный шаг в направлении реализации глобального проекта Физика, ибо они превращают умозрительную «натуральную философию» в количественную науку! ЗН-II - это дифференциальное уравнение, решив которое мы решаем основную задачу механики - находим траекторию тела (или системы тел, если для каждого из них записать свой ЗН-II ) под действием тех или иных сил, действующих как между телами, входящими в систему, так и, возможно, сторонних (которые тоже можно добавить в суммы в правой части уравнений ЗН-II). Но надо уметь решать дифференциальные уравнения и их системы! И тут мы подходим к главному достижению сэра Исаака Ньютона, делающему его человеком, внесшим, возможно, наибольший вклад в развитие человеческой цивилизации среди всех людей, живших до и после него: это разработка математического аппарата дифференциального и интегрального исчисления! позволившая человечеству сделать колоссальный прорыв не только в понимании устройства Вселенной, но и в технике и в технологиях.

Isaac Newton и его главный труд Сэр Айзек Ньютон (Isaac Newton, 1643 -1727) и его главный труд «Натуральная Философия и Принципы Математики» , Лондон, 1687 год.

Механика Ньютона Мы упомянули второй и третий законы механики Ньютона. А где же первый, спросите Вы? А первый, как пишут в учебниках, состоит в утверждении, что инерциальные системы отсчета (в которых выполняется Второй закон Ньютона) - существуют Это далеко не тривиальное утверждение. Система отсчета должна быть привязана к некоторому телу отсчета. Ясно, что если мы найдем хотя-бы одну такую систему, то мы найдем сразу их все, ибо те, что движутся относительно нее равномерно и прямолинейно тоже будут инерциальными. Но где найти хоть одну? Ясно, что системы, привязанные к поверхности Земли, строго говоря, инрерциальными не являются, поскольку Земля вращается - т. е. ее поверхность движется заведомо не прямолинейно.

Механика Ньютон полагал, что строго инерциальной можно считать, например, систему, связанную с неподвижным Солнцем или с неподвижными-же далекими от нас звездами. Это утверждение до сих пор часто повторяют в школьных учебниках, хотя сегодня мы прекрасно знаем, что Солнце тоже вращается - как вокруг своей оси, так и как целое - вокруг центра Галактики, и все остальные звезды тоже вращаются и движутся неравномерно и непрямолинейно, хотя это и не так заметно на огромном расстоянии. Поэтому сегодня первый закон Ньютона разумнее сформулировать иначе, с учетом важнейшего перво-принципа, которому, судя по всему, подчиняется все во Вселенной и в нашей жизни: ничего абсолютно точного и идеального в природе не бывает. Нет, судя по всему, и тел отсчета, привязанные к которым системы отсчета можно было бы считать идеально инерциальными. НО! Почти инерциальные (в пределах тосности, необходимой для решения той или иной задачи) системы найти можно и достаточно не сложно.

Механика Ньютона Если рассматривать движения в масштабах много меньших радиуса Земли и с характерными временами, много меньшими ее периода вращения - то вполне удовлетворительно инерциальными оказываются любые системы отсчета, привязанные к поверхности Земли ( «лабораторные» системы отсчета) либо движущиеся относительно нее равномерно и прямолинейно. В следующих нескольких эпизодах нашего курса мы будем в основном работать именно с такими системами.