Импульс и однородность пространства Ольчак Lekcja_06_2015_11.ppt
- Количество слайдов: 13

Глобальный проект «Физика» Автор: Доцент НИЯУ МИФИ, к. ф. -м. н. , Ольчак Андрей Станиславович Лекция 06 Импульс и однородность пространства

Энергия и однородность свойств времени На прошлом занятии мы выяснили, что свойство однородности времени, наблюдаемое в инерциальных системах отсчета, приводит к необходимости сохранения в замкнутых механических системах некоторой величины, называемой энергией: E = T + U = Σmiq'i 2/2 + U(q) = Const! где T - кинетическая энергия системы, а U(q) - ее суммарная потенциальная энергия, зависящая от координат всех тел системы. Энергия, являющаяся физической мерой способности системы совершить механическую работу, сохраняется в силу однородности свойств времени. Проверим теперь, не будет ли иметь аналогичных последствий также и свойство однородности пространства в инерциальных системах отсчета.

Однородность пространства и импульс Требование однородности свойств пространства означает, что при смещении всей системы (т. е. смещении всех ее точек) на некоторый вектор ε функция Лагранжа системы и ее уравнения движения остаются неизменными. Если направить одну из осей координат (ось х, например) в направлении вектора смещения и считать, что смещение εх мало, то изменение функции Лагранжа δL = Σ εх L/ хi = εхΣ L/ хi , где суммирование выполняется по всем частицам (от 1 до N). Учитывая уравнения Лагранжа, можно представить в виде δL выполняем преобразования: δL = εхΣ L/ хi = εхΣ d( L/ vxi)/dt = εх d (Σ L/ vxi)/dt = 0 => => Σ L/ vxi = Σpxi = Σmvxi = Px = Const, величины pxi = L/ vxi = mvxi являются х-компонентами векторов импульсов отдельных частиц системы. Суммарный импульс системы Px = Σmvxi , если при переносе в направлении х свойства системы не меняются, сохраняется (!). Если свойства системы не меняются при переносе в любом направлении сохраняется и весь вектор суммарного импульса P = Σmvi = Const

Однородность пространства и импульс Неизменность свойств системы при переносе нее как целого на какой-то отрезок (однородность пространства) предполагает отсутствие внешних сил, действующих на систему, когда выражение для потенциальной энергии системы разбивается на сумму потенциальных энергий взаимодействия отдельных пар тел, зависящих только от модулей разности радиус-векторов этих тел: . U(r 1, r 2, …, ri, . . . ) = ΣΣU(|ri-rj |). здесь двойная сумма берется по всем возможным значениям индексов i и j, за исключением слагаемых с i = j, что означает, что мы исключаем из рассмотрения (пока!) возможность взаимодействия отдельных точек с самими собой. Такая потенциальная энергия при замене каждого ri на ri - ε очевидно не меняется. Отдельные пространственные компоненты суммарного вектора импульса системы могут сохраняться и при наличии внешних сил, если их действие на каждую частицу системы в данном направлении полностью скомпенсировано. В принципе, для вывода закона сохранения импульса применение обобщенной механики и уравнений Лагранжа не обязательно. Доказать его можно оставаясь и в рамках формализма законов Ньютона.

Закон сохранения импульса Если у нас есть система из нескольких тел, взаимодействующих друг с другом с Fij, (где i и j - номера объектов, входящих в систему), а также, возможно, с какими то сторонними (внешними) объектами с силами Fiстор, то для описания силами их движения придется записать целую систему уравнений ЗН-II: dp 1/dt = ΣFi 1+F 1 стор dp 2/dt = ΣFi 2 +F 2 стор , и т. д. Просуммируем теперь все уравнения системы: левые и правые части. При этом = U(|ri-rj |)/ ri = - U(|ri-rj |)/ rj = -Fij. (мы тут попутно убеждаемся в справедливости 3 -его закона Ньютона), а Fii = -Fii = 0, - то есть учтем. что Fij сами с собой тела не взаимодействуют, что вполне естественно. Σdpi/dt = ΣΣFij+ΣFi стор Двойная сумма берется по обоим индексам i и j. В этой сумме для каждого слагаемого с индексами Fij обязательно найдется слагаемое с индексами, расположенными в обратном порядке Fji и сложившись, в соответствии с ЗН_III, каждая такая пара даст ноль. В правой части уравнения останутся только сторонние силы.

Закон сохранения импульса Σdpi/dt = d(Σpi)/dt = ΣFi стор => d. P/dt = Fстор P = Σpi = Σmivi - суммарный импульс всех тел системы, а - Fстор сумма где всех сторонних сил, действующих на все тела системы. СЛЕДСТВИЕ: если сторонних сил нет или они скомпенсированы (Fстор = 0 ), то суммарный импульс системы остается постоянным, как бы не двигались и не взаимодействовали тела системы между собой! d. P/dt = 0 => P = Σpi = Const Подчеркнем, однако, что хотя для доказательства закона сохранения импульса формализм уравнений Лагранжа и не обязателен, но он наглядно подчеркивает прямую логическую связь факта сохранения импульса системы и однородности свойств пространства, подобно тому, как для сохранения энергии необходимо и достаточно, чтобы неизменными (однородными) оставались свойства времени.

Импульс в разных системах отсчета Итак, свойство однородности пространства автоматически имеет следствием закон сохранения полного импульса в замкнутых системах: P = Σmvi = Const Величина наблюдаемого импульса как отдельных материальных точек, так и всей системы в целом, равно как и величина кинетической энергии системы, зависят от системы отсчета. Напомним, что в основе всей современной механики лежит осознание относительности движения и наблюдаемой скорости. В разных инерциальных системах отсчета наблюдаемые скорости будут казаться разными, и, соответственно, разными будут их импульсы и кинетические энергии. И хотя, с точки зрения законов механики все инерциальные системы равноправны, среди них выделяется одна, особенно удобная для описания движения - система центра масс или центра инерции, о которой мы и поговорим сегодня.

Система центра масс Главное свойство системы центра масс или центра инерции, состоит в том, что в ней полный импульс системы точно равен нулю, а полная кинетическая энергия - минимальна. Если в некоторой лабораторной системе отсчета частицы системы имеют скорости vi и суммарный импульс системы равен P = Σmivi , то в системе центра масс скорости всех частиц будут отличаться на вектор V = P/ Σmi так, чтобы суммарный импульс Pсцм = Σmi(vi - V) = 0 Эта система отсчета обычно привязывается к точке, называемой центром масс или центром инерции системы.
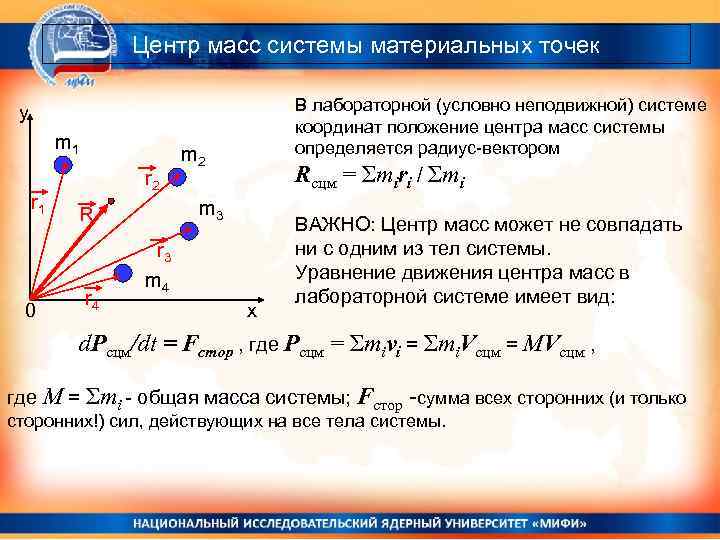
Центр масс системы материальных точек В лабораторной (условно неподвижной) системе координат положение центра масс системы определяется радиус-вектором y m 1 r 1 0 r 2 Rсцм = Σmiri / Σmi m 3 R r 4 m 2 r 3 m 4 x ВАЖНО: Центр масс может не совпадать ни с одним из тел системы. Уравнение движения центра масс в лабораторной системе имеет вид: d. Pсцм/dt = Fстор , где Pсцм = Σmivi = Σmi. Vсцм = MVсцм , где M = Σmi - общая масса системы; Fстор -сумма всех сторонних (и только сторонних!) сил, действующих на все тела системы.

Энергия в системе центра масс y m 1 r 2 m 3 R r 3 m 4 Энергию покоящейся как целое системы материальных точек (то есть энергию, измеренную в системе отсчета, связанной с центром масс), называют обычно внутренней энергией системы Eсцм. Она складывается из кинетических энергий всех частиц в СЦМ и общей потенциальной энергии, не зависящей от скорости инерциальной системы отсчета. В любой другой инерциальной системе 0 x отсчета, движущейся относительно СЦМ со скоростью V, полная энергия будет всегда больше и равна E = MV 2/2 + Eсцм. Докажем последнее утверждение. r 4 E = Σmivi 2/2 + U = Σmi(V +vi сцм)2/2 + U = = MV 2/2 + (Σmivi сцм, V) + (Σmivi сцм 2/2 + U) = MV 2/2 + 0 + Eсцм.
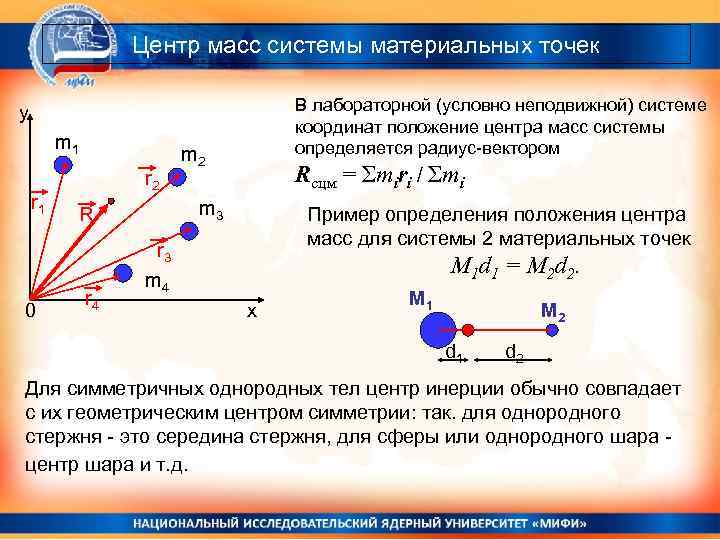
Центр масс системы материальных точек В лабораторной (условно неподвижной) системе координат положение центра масс системы определяется радиус-вектором y m 1 r 1 0 r 2 Rсцм = Σmiri / Σmi m 3 R r 4 m 2 Пример определения положения центра масс для системы 2 материальных точек r 3 m 4 М 1 d 1 = M 2 d 2. x М 1 М 2 d 1 d 2 Для симметричных однородных тел центр инерции обычно совпадает с их геометрическим центром симметрии: так. для однородного стержня - это середина стержня, для сферы или однородного шара центр шара и т. д.

Задачи 1. Доказать свойство положения центра масс системы двух тел М 1 d 1 = M 2 d 2. М 2 d 1 d 2 2. Найти координаты расстояние R от центра масс кочерги, согнутой из однородного стержня, до ее точки сгиба, если стороны кочерги имеют длины L 1 и L 2 R L 1

Задачи 2. Найти координаты расстояние R от центра масс кочерги, согнутой из однородного стержня, до ее точки сгиба, если стороны кочерги имеют длины L 1 и L 2. РЕШЕНИЕ: центр масс в силу симметрии находится на линии, соединяющей середины (центры масс) сторон кочерги, и положение его можно найти по формуле для системы 2 тел: М 1 d 1 = M 2 d 2 => L 1 d 1 = L 2 d 2 L 2 R d 1 Учтено, что массы частей однородного стержня пропорциональны их длинам. С другой стороны, по теореме Пифагора: (L 1/2)2 + (L 2/2)2 = (d 1 + d 2)2 , и L 1 R 2 = (d 2 L 1/2(d 1+d 2))2 + (d 1 L 2/2(d 1+d 2))2 = ((d 2 L 1)2+(d 1 L 2)2 )/(L 12+L 22) Решая полученную систему уравнений, находим R = (L 14 + L 24)1/2/2(L 1 +L 2)
Импульс и однородность пространства Ольчак Lekcja_06_2015_11.ppt