fd0b245685e3b660ee48ef9d3bc34369.ppt
- Количество слайдов: 138

Glencoe Geometry Interactive Chalkboard Copyright © by The Mc. Graw-Hill Companies, Inc. Developed by FSCreations, Inc. , Cincinnati, Ohio 45202 Send all inquiries to: GLENCOE DIVISION Glencoe/Mc. Graw-Hill 8787 Orion Place Columbus, Ohio 43240

Lesson 1 -1 Points, Lines, and Planes Lesson 1 -2 Linear Measure and Precision Lesson 1 -3 Distance and Midpoints Lesson 1 -4 Angle Measure Lesson 1 -5 Angle Relationships Lesson 1 -6 Polygons
Example 1 Name Lines and Planes Example 2 Model Points, Lines, and Planes Example 3 Draw Geometric Figures Example 4 Interpret Drawings

Use the figure to name a line containing point K. Answer: The line can be named as line a. There are three points on the line. Any two of the points can be used to name the line.
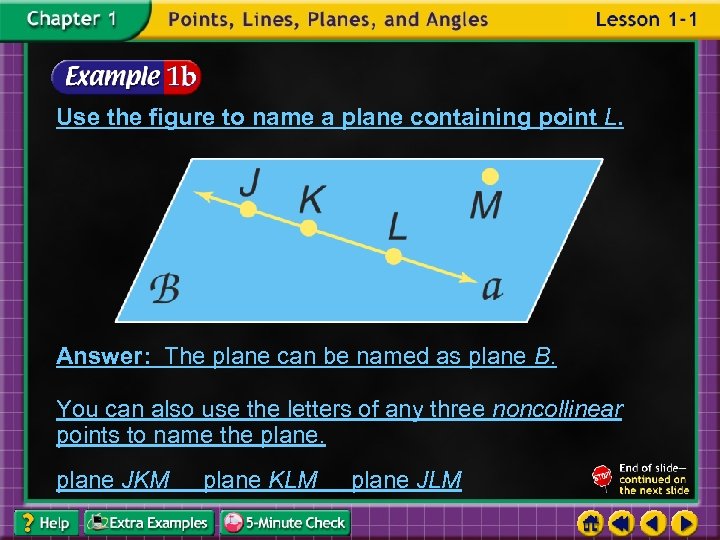
Use the figure to name a plane containing point L. Answer: The plane can be named as plane B. You can also use the letters of any three noncollinear points to name the plane JKM plane KLM plane JLM

The letters of each of these names can be reordered to create other acceptable names for this plane. For example, JKM can also be written as JMK, MKJ, KJM, KMJ, and MJK. There are 18 different three-letter names for this plane.
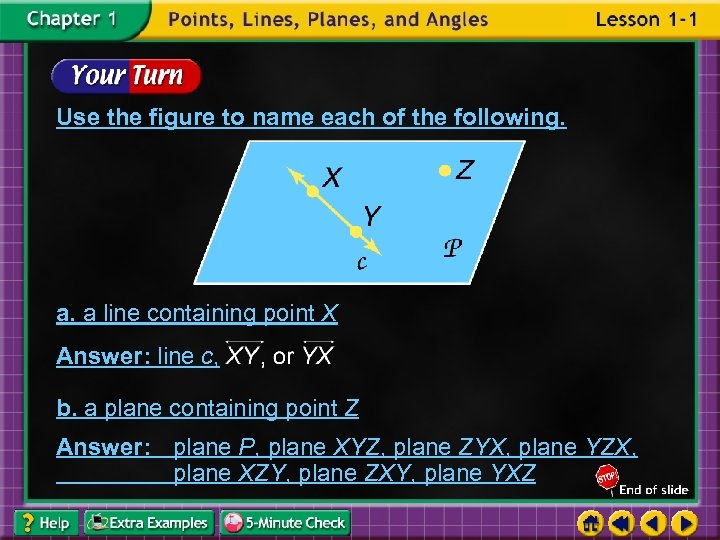
Use the figure to name each of the following. a. a line containing point X Answer: line c, b. a plane containing point Z Answer: plane P, plane XYZ, plane ZYX, plane YZX, plane XZY, plane ZXY, plane YXZ
VISUALIZATION Name the geometric shape modeled by the long hand on a clock. Answer: The long hand on a clock models a line segment.

VISUALIZATION Name the geometric shape modeled by a 10 12 patio. Answer: The patio models a plane.

VISUALIZATION Name the geometric shape modeled by the location where the corner of a driveway meets the road. Answer: The location where the corner of a driveway meets the road models a point.
VISUALIZATION Name the geometric shape modeled by each object. a. a colored dot on a map used to mark the location of a city Answer: point b. the ceiling of your classroom Answer: plane c. the railing on a stairway Answer: line segment

Draw and label a figure for the following situation. Plane R contains lines and , which intersect at point P. Add point C on plane R so that it is not collinear with or. Draw a surface to represent plane R and label it.
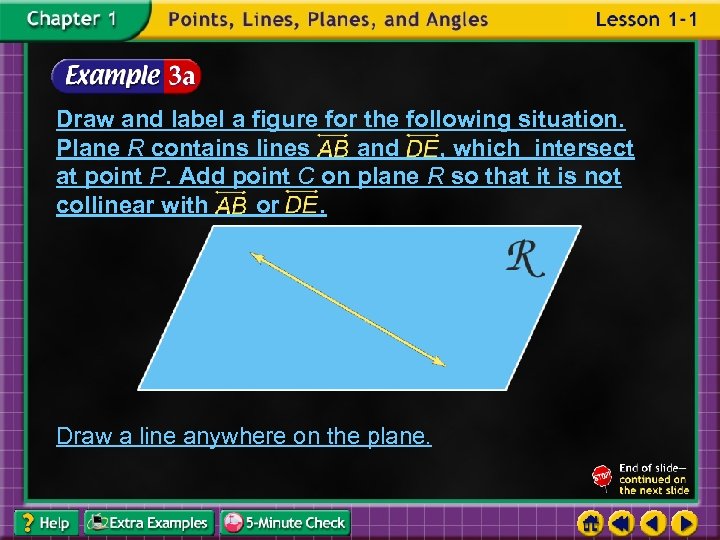
Draw and label a figure for the following situation. Plane R contains lines and , which intersect at point P. Add point C on plane R so that it is not collinear with or. Draw a line anywhere on the plane.
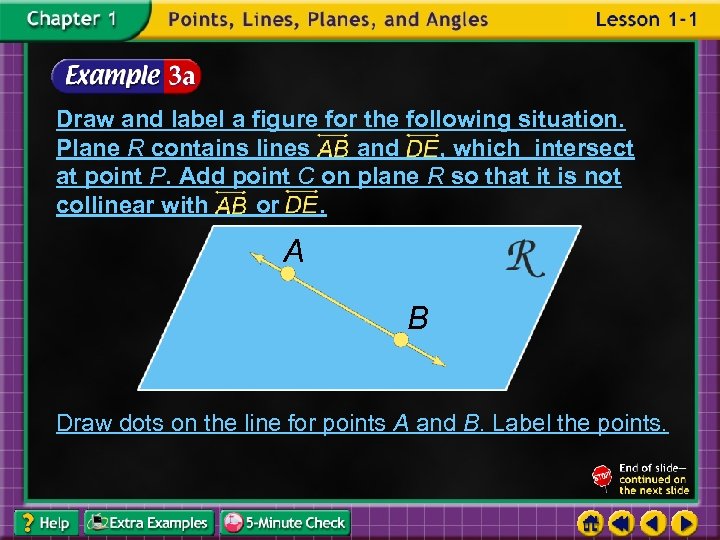
Draw and label a figure for the following situation. Plane R contains lines and , which intersect at point P. Add point C on plane R so that it is not collinear with or. A B Draw dots on the line for points A and B. Label the points.
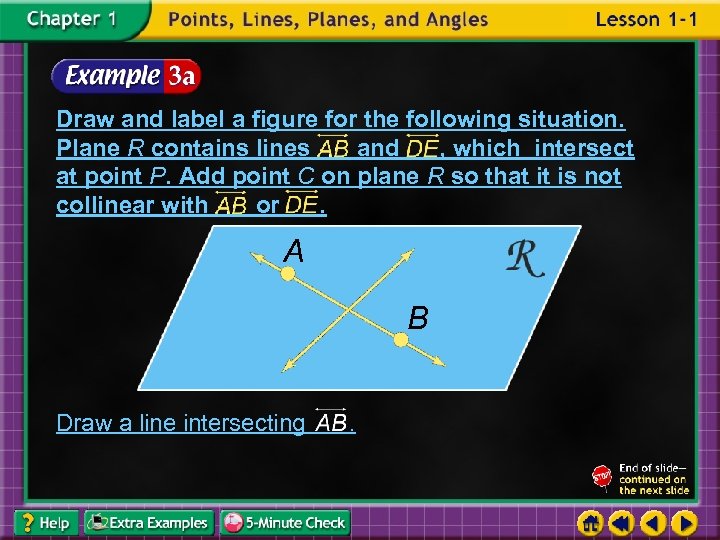
Draw and label a figure for the following situation. Plane R contains lines and , which intersect at point P. Add point C on plane R so that it is not collinear with or. A B Draw a line intersecting .
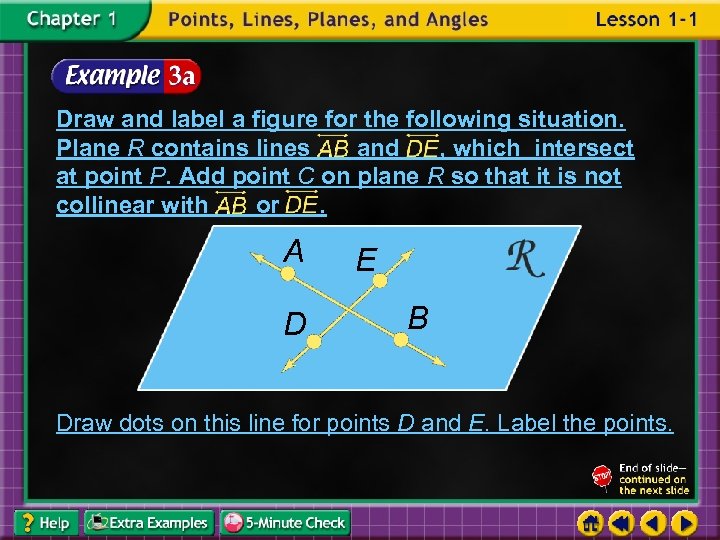
Draw and label a figure for the following situation. Plane R contains lines and , which intersect at point P. Add point C on plane R so that it is not collinear with or. A D E B Draw dots on this line for points D and E. Label the points.

Draw and label a figure for the following situation. Plane R contains lines and , which intersect at point P. Add point C on plane R so that it is not collinear with or. A E D P B Label the intersection point of the two lines as P.

Draw and label a figure for the following situation. Plane R contains lines and , which intersect at point P. Add point C on plane R so that it is not collinear with or. Answer: A C E D P B Draw a dot for point C in plane R such that it will not lie on or. Label the point.
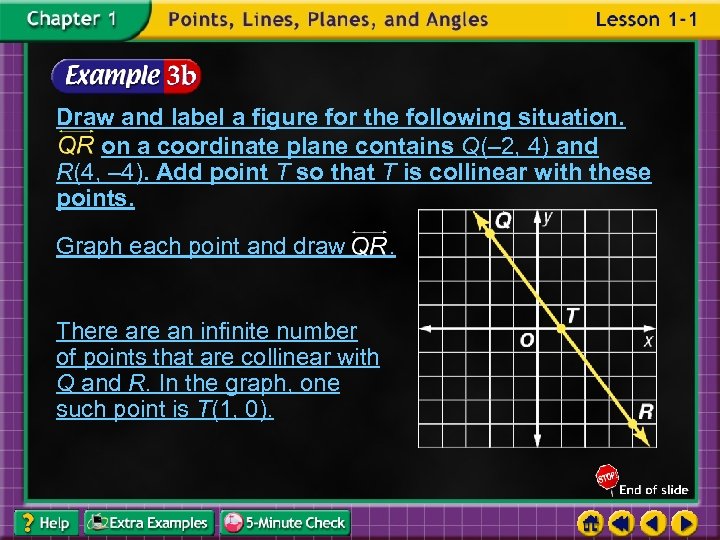
Draw and label a figure for the following situation. on a coordinate plane contains Q(– 2, 4) and R(4, – 4). Add point T so that T is collinear with these points. Graph each point and draw There an infinite number of points that are collinear with Q and R. In the graph, one such point is T(1, 0). .

Draw and label a figure for each relationship. a. Plane D contains line a, line m, and line t, with all three lines intersecting at point Z. Add point F on plane D so that it is not collinear with any of the three given lines. Sample answer:

Draw and label a figure for each relationship. b. on a coordinate plane contains B(– 3, – 2) and A(3, 2). Add point M so that M is collinear with these points. Sample answer:

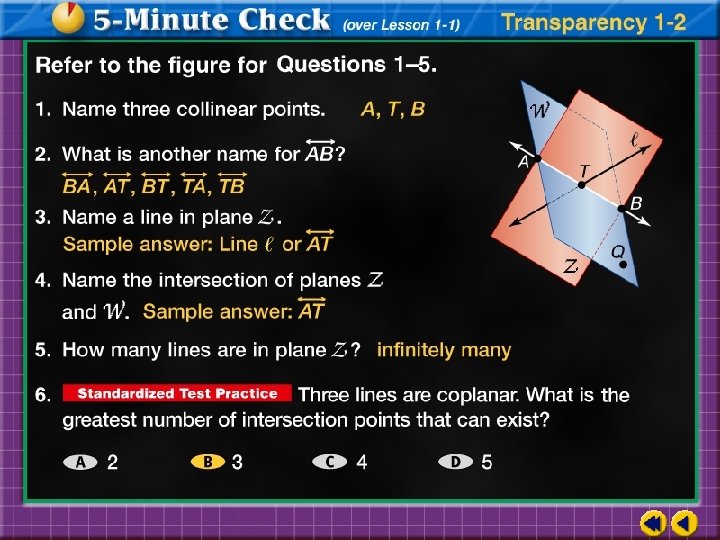
How many planes appear in this figure? Answer: There are two planes: plane S and plane ABC.
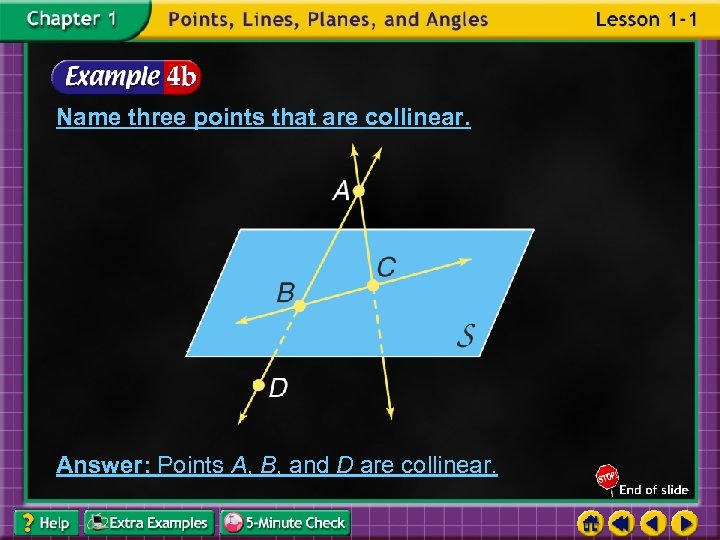
Name three points that are collinear. Answer: Points A, B, and D are collinear.

Are points A, B, C, and D coplanar? Explain. Answer: Points A, B, C, and D all lie in plane ABC, so they are coplanar.

At what point do and intersect? Answer: The two lines intersect at point A.

a. How many planes appear in this figure? Answer: two

b. Name three points that are collinear. Sample answer: A, X, and Z

c. Are points X, O, and R coplanar? Explain. Answer: Points X, O, and R all lie in plane T, so they are coplanar.
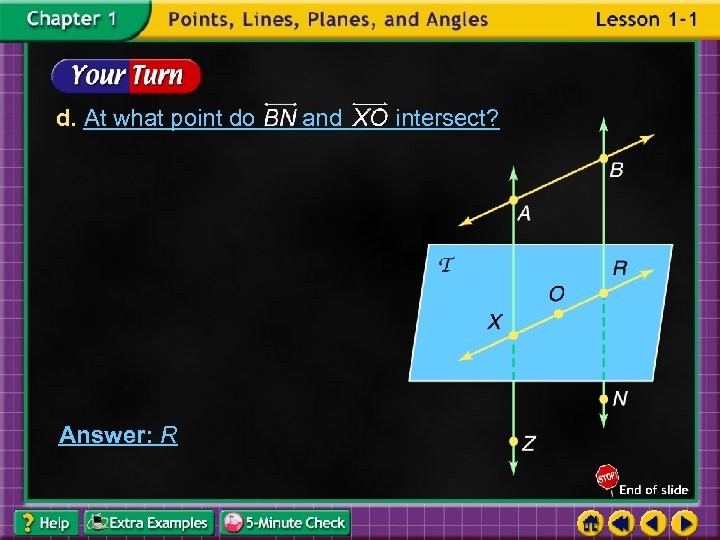
d. At what point do Answer: R and intersect?


Example 1 Length in Metric Units Example 2 Length in Customary Units Example 3 Precision Example 4 Find Measurements Example 5 Congruent Segments

Find the length of . The long marks are centimeters, and the shorter marks are millimeters. There are 10 millimeters for each centimeter. Answer: is about 42 millimeters long.
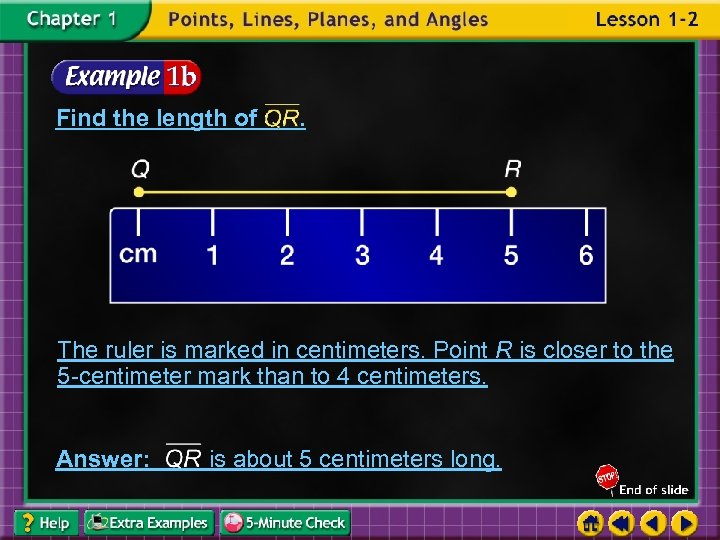
Find the length of . The ruler is marked in centimeters. Point R is closer to the 5 -centimeter mark than to 4 centimeters. Answer: is about 5 centimeters long.

a. Find the length of Answer: 18 mm
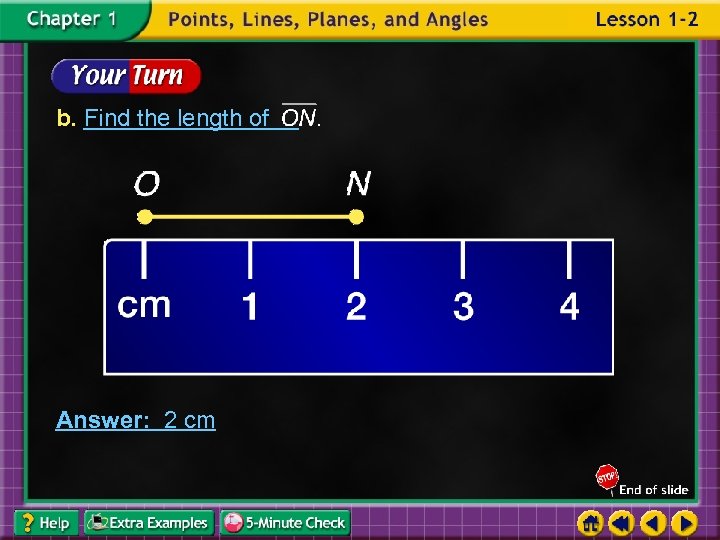
b. Find the length of Answer: 2 cm
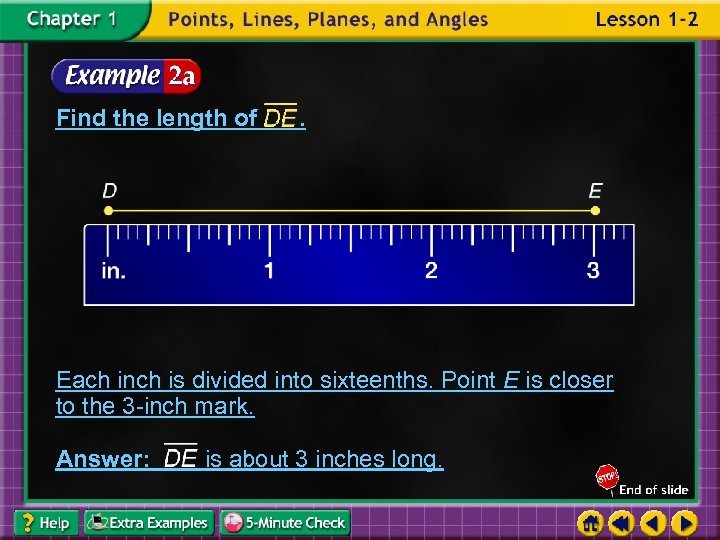
Find the length of . Each inch is divided into sixteenths. Point E is closer to the 3 -inch mark. Answer: is about 3 inches long.
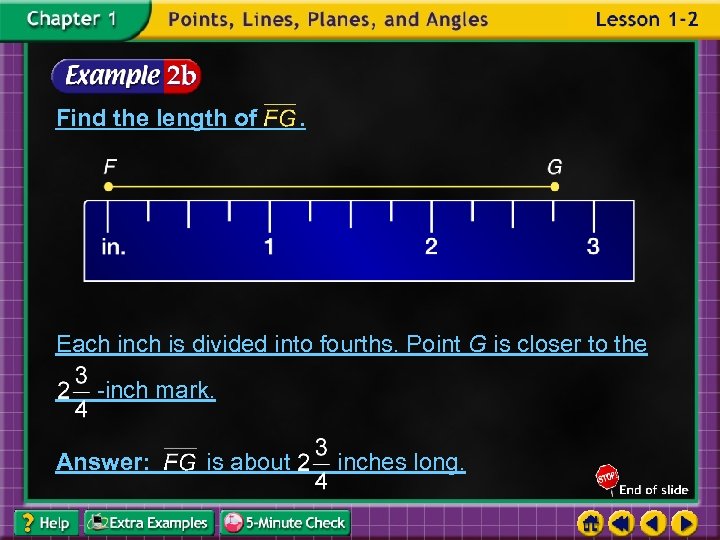
Find the length of . Each inch is divided into fourths. Point G is closer to the -inch mark. Answer: is about inches long.
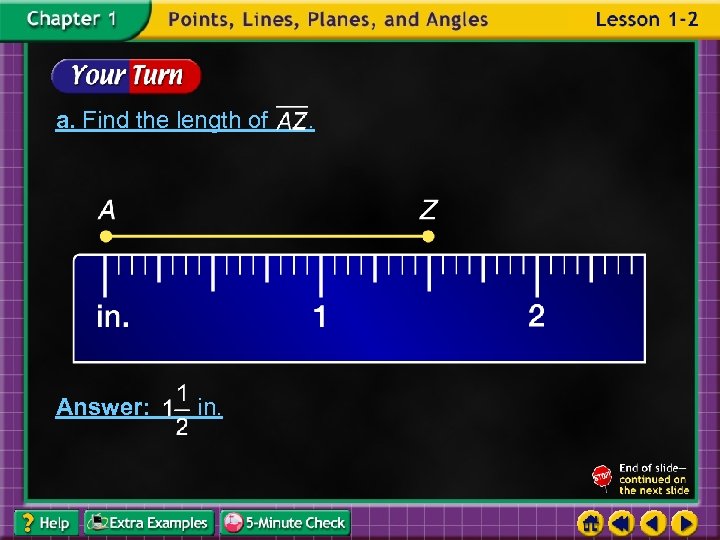
a. Find the length of Answer: in. .
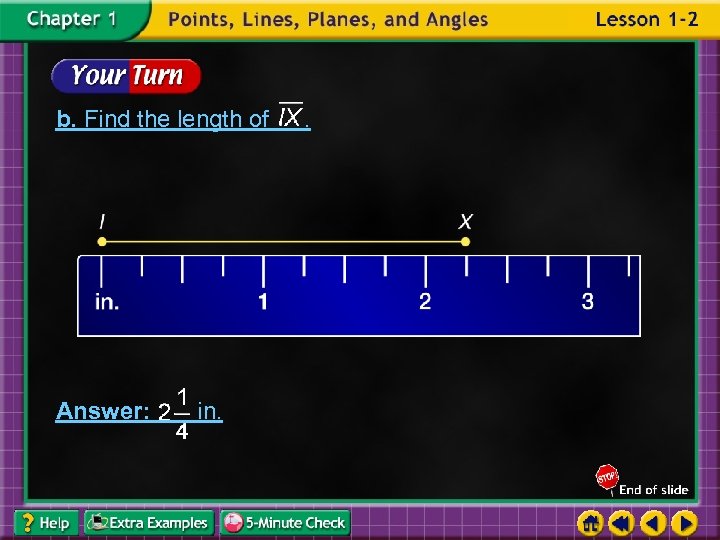
b. Find the length of Answer: in. .

Find the precision for inches. Explain its meaning. The measuring tool is divided into -inch increments. Thus, the measurement is precise to within Answer: The precision is be inches to inch. The measurement could inches.

Find the precision for 15 millimeters. Explain its meaning. The measuring tool is divided into millimeter increments. Thus, the measurement is precise to within (1) or 0. 5 millimeter. Answer: The precision is 0. 5 millimeter. The measurement could be 14. 5 millimeters to 15. 5 millimeters.
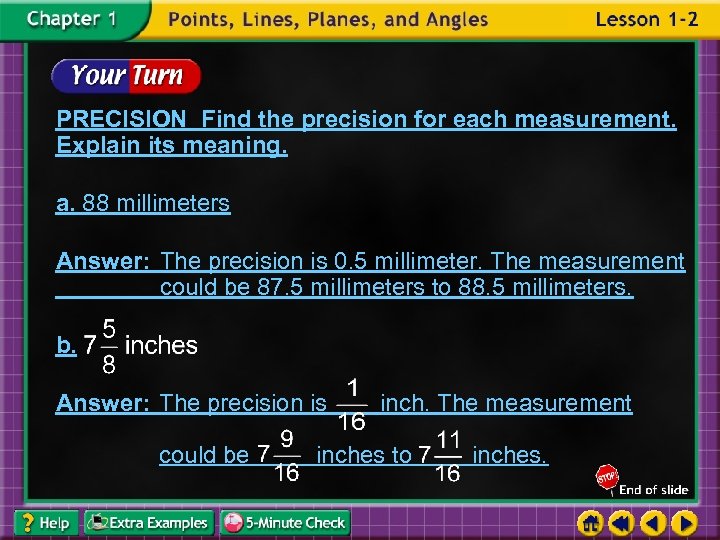
PRECISION Find the precision for each measurement. Explain its meaning. a. 88 millimeters Answer: The precision is 0. 5 millimeter. The measurement could be 87. 5 millimeters to 88. 5 millimeters. b. Answer: The precision is could be inch. The measurement inches to inches.

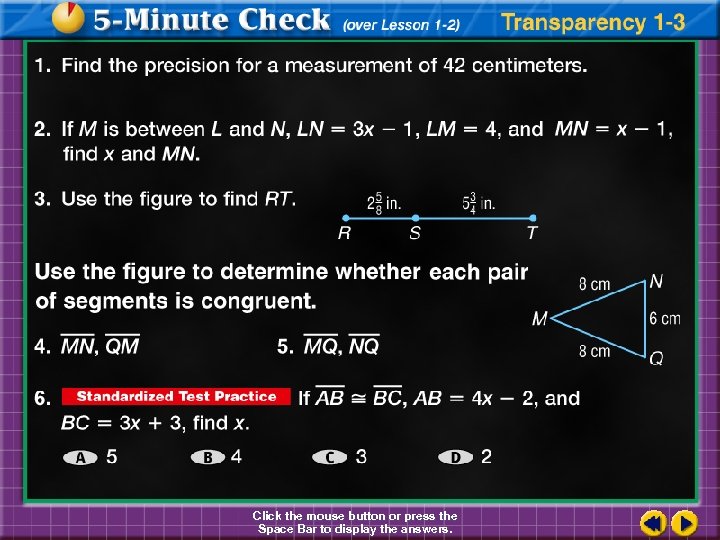
Find LM. LM is the measure of . Point M is between L and N. Sum of parts whole Substitution Subtract 2. 6 from each side. Simplify. Answer: is 1. 4 centimeters long.

Find XZ. XZ is the measure of . Point Y is between X and Z. XZ can be found by adding XY and YZ. Sum of parts Substitution Add. whole

Answer: is inches long.

Find x and ST if T is between S and U, ST and TU 5 x – 3. 7 x, SU Substitute known values. Add 3 to each side. Simplify. Divide each side by 12. Simplify. 45,
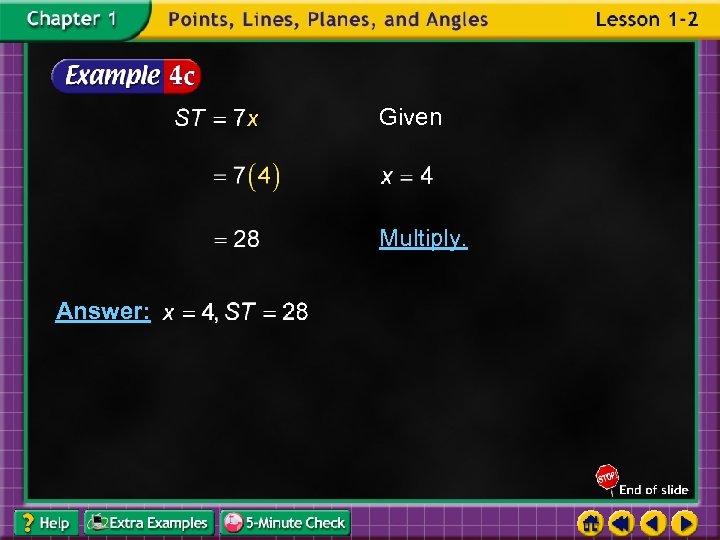
Given Multiply. Answer:
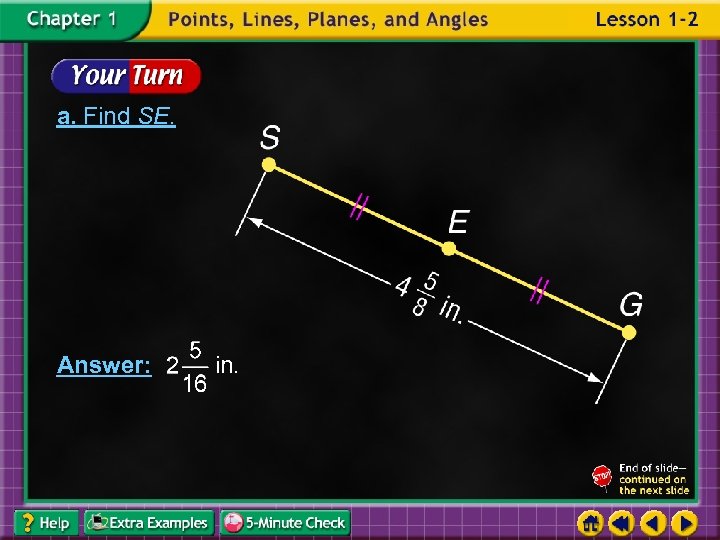
a. Find SE. Answer: in.
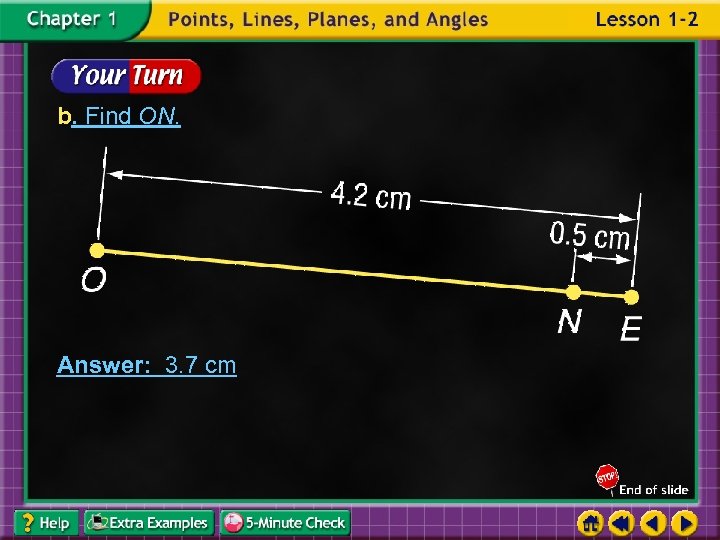
b. Find ON. Answer: 3. 7 cm

c. Find a and AB if AB 4 a + 10, BC Answer: 3 a – 5, and AC 19.

FONTS The Arial font is often used because it is easy to read. Study the word time shown in Arial type. Each letter can be broken into individual segments. The letter T would have two segments, a short horizontal segment, and a long vertical segment. Assume that all segments overlap when they meet. Which segments are congruent? TIME Answer: The five vertical segments in the letters T, I, M, and E are congruent. The four horizontal segments in T and E are congruent. The two diagonal segments in the letter M are congruent.

LEISURE ACTIVITIES The graph shows the percent of adults who participated in selected activities. Suppose a segment was drawn along the height of each bar. Which categories would have segments that are congruent?

Answer: The segments on the bars for going to museums and picnics would be congruent because they both have the same height, representing 16%. The segments on bars for going to the zoo and playing board games would be congruent because they have the same height, representing 14%.

Example 1 Find Distance on a Number Line Example 2 Find Distance on a Coordinate Plane Example 3 Find Coordinates of Midpoint Example 4 Find Coordinates of Endpoint Example 5 Use Algebra to Find Measures

Use the number line to find QR. The coordinates of Q and R are – 6 and – 3. Distance Formula Simplify. Answer: 3

Use the number line to find AX. Answer: 8
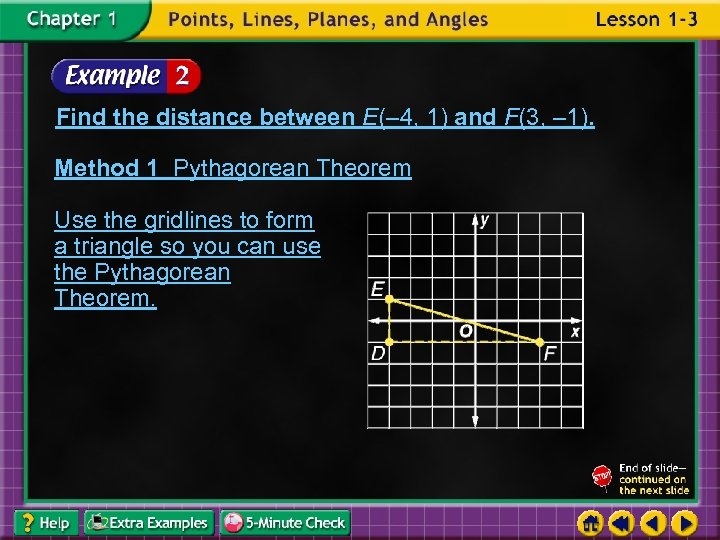
Find the distance between E(– 4, 1) and F(3, – 1). Method 1 Pythagorean Theorem Use the gridlines to form a triangle so you can use the Pythagorean Theorem.
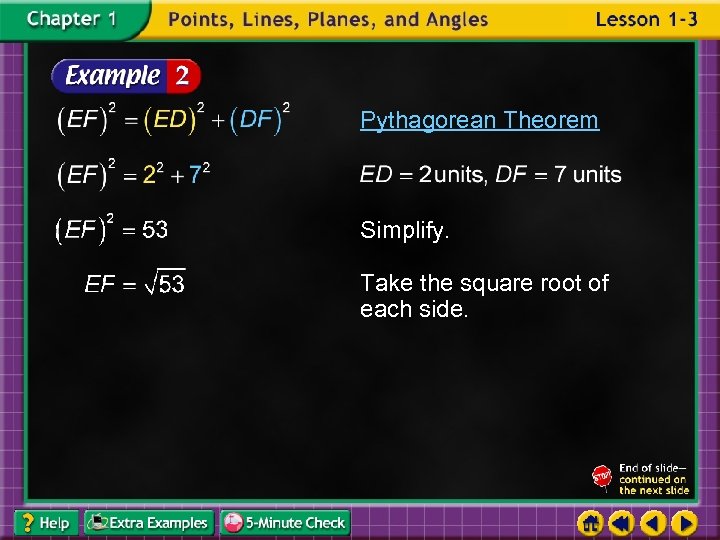
Pythagorean Theorem Simplify. Take the square root of each side.
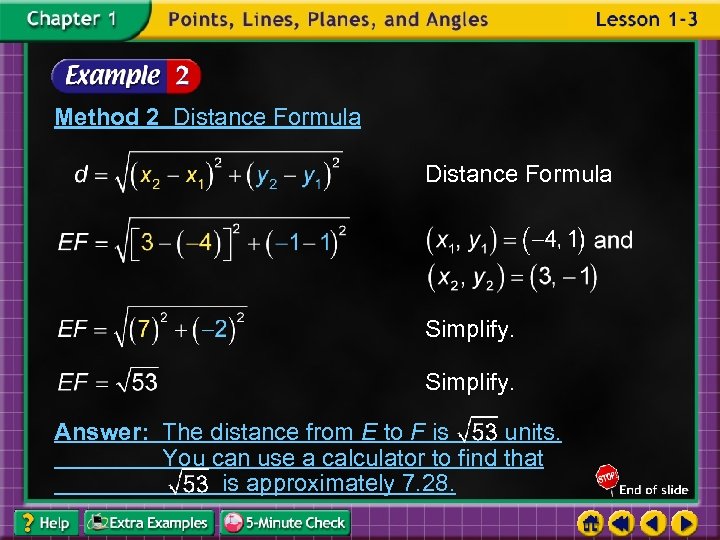
Method 2 Distance Formula Simplify. Answer: The distance from E to F is units. You can use a calculator to find that is approximately 7. 28.

Find the distance between A(– 3, 4) and M(1, 2). Answer:
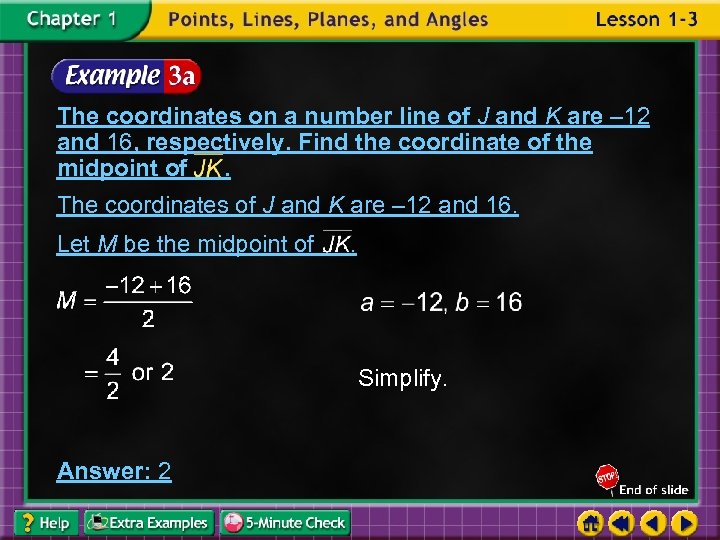
The coordinates on a number line of J and K are – 12 and 16, respectively. Find the coordinate of the midpoint of. The coordinates of J and K are – 12 and 16. Let M be the midpoint of . Simplify. Answer: 2
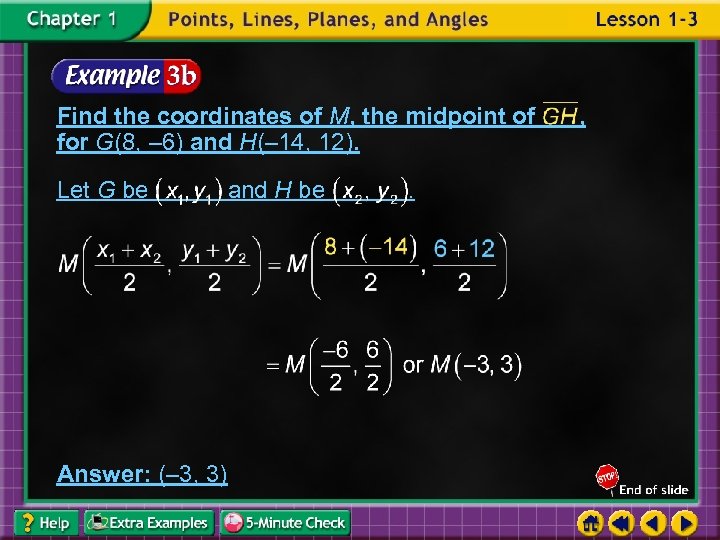
Find the coordinates of M, the midpoint of for G(8, – 6) and H(– 14, 12). Let G be Answer: (– 3, 3) and H be . ,

a. The coordinates on a number line of Y and O are 7 and – 15, respectively. Find the coordinate of the midpoint of. Answer: – 4 b. Find the coordinates of the midpoint of for X(– 2, 3) and Y(– 8, – 9). Answer: (– 5, – 3)
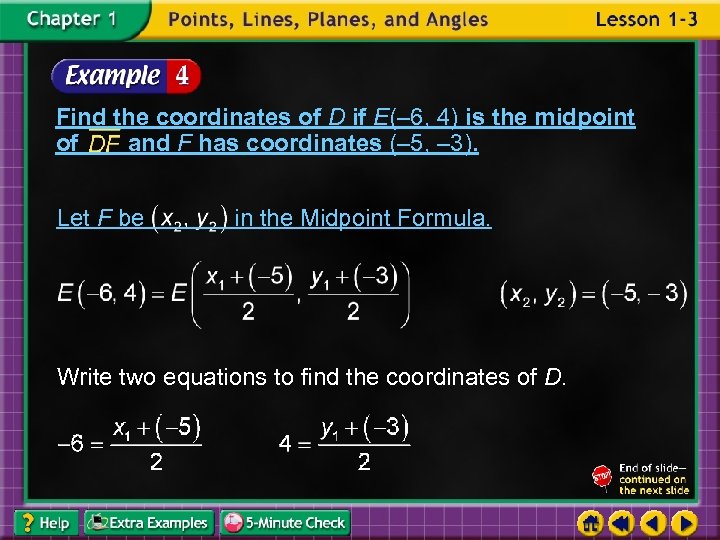
Find the coordinates of D if E(– 6, 4) is the midpoint of and F has coordinates (– 5, – 3). Let F be in the Midpoint Formula. Write two equations to find the coordinates of D.

Solve each equation. Multiply each side by 2. Add 5 to each side. Multiply each side by 2. Add 3 to each side. Answer: The coordinates of D are (– 7, 11).
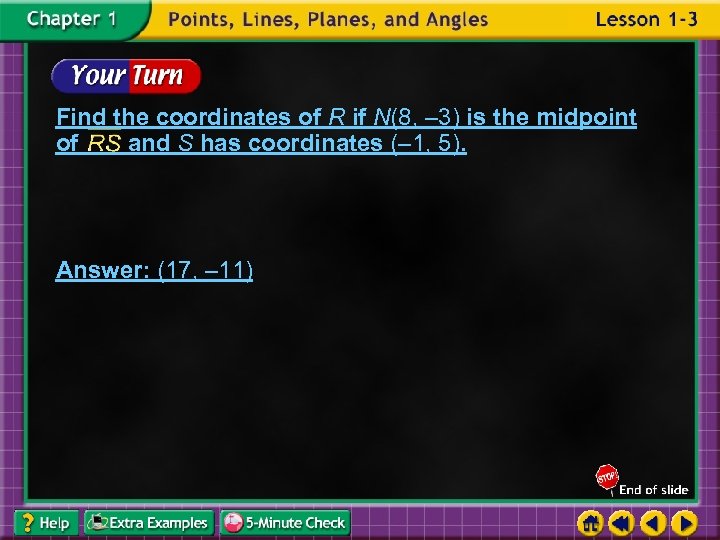
Find the coordinates of R if N(8, – 3) is the midpoint of and S has coordinates (– 1, 5). Answer: (17, – 11)
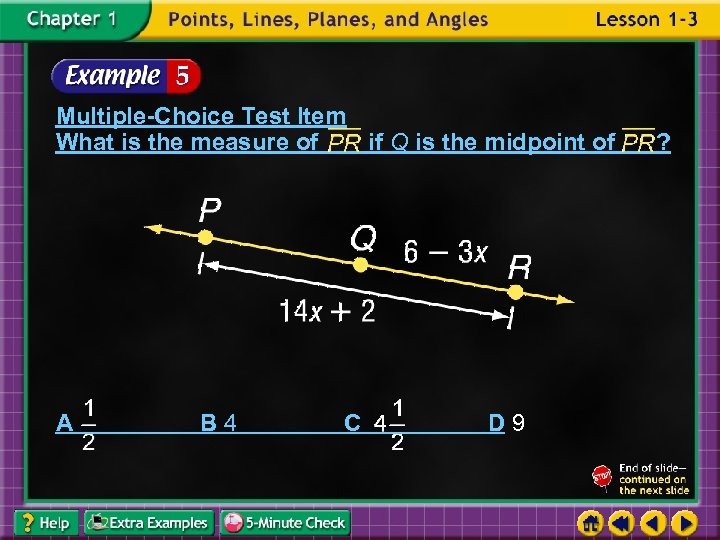
Multiple-Choice Test Item What is the measure of if Q is the midpoint of A B 4 C D 9 ?
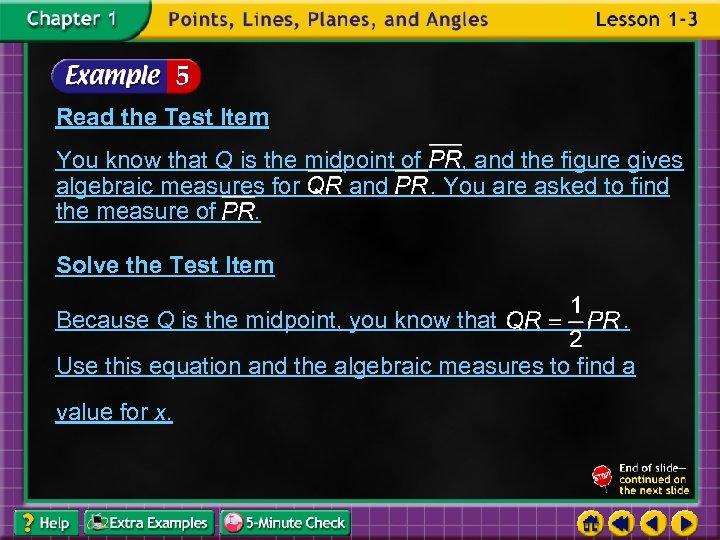
Read the Test Item You know that Q is the midpoint of , and the figure gives algebraic measures for and. You are asked to find the measure of. Solve the Test Item Because Q is the midpoint, you know that . Use this equation and the algebraic measures to find a value for x.

Definition of midpoint Distributive Property Subtract 1 from each side. Add 3 x to each side. Divide each side by 10.

Now substitute for x in the expression for PR. Original measure Simplify. Answer: D
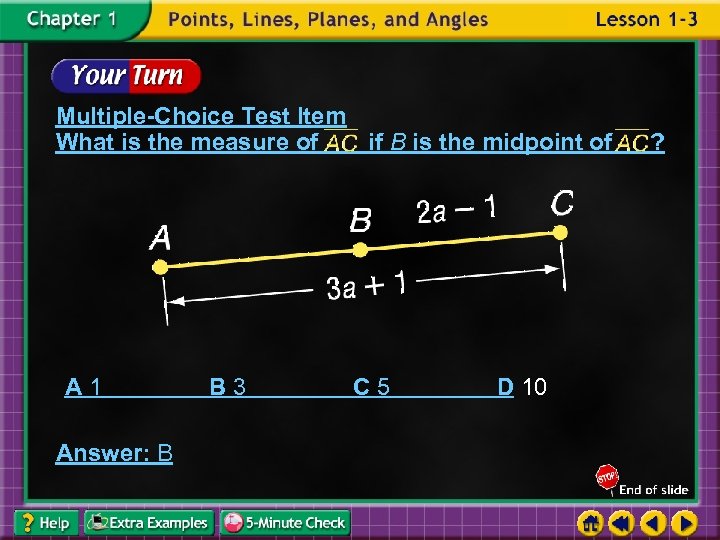
Multiple-Choice Test Item What is the measure of if B is the midpoint of A 1 Answer: B B 3 C 5 D 10 ?


Example 1 Angles and Their Parts Example 2 Measure and Classify Angles Example 3 Use Algebra to Find Angle Measures
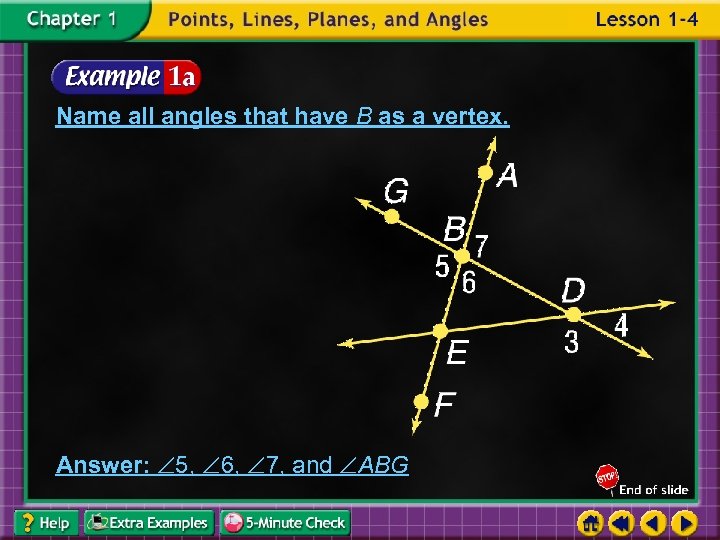
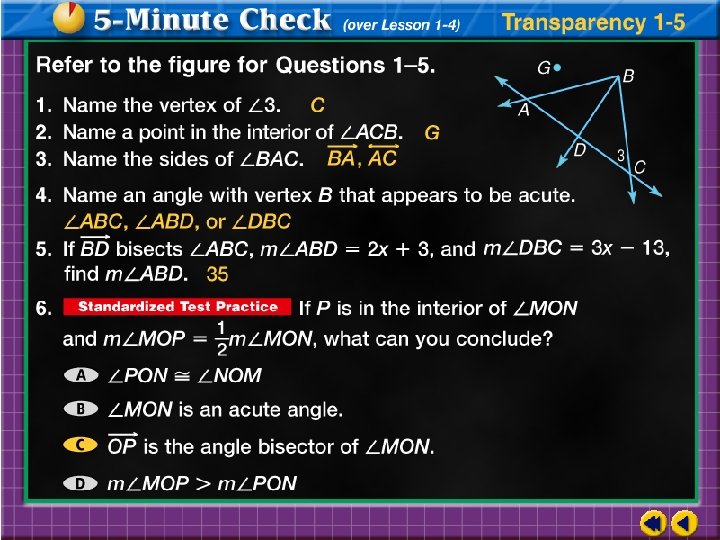
Name all angles that have B as a vertex. Answer: 5, 6, 7, and ABG
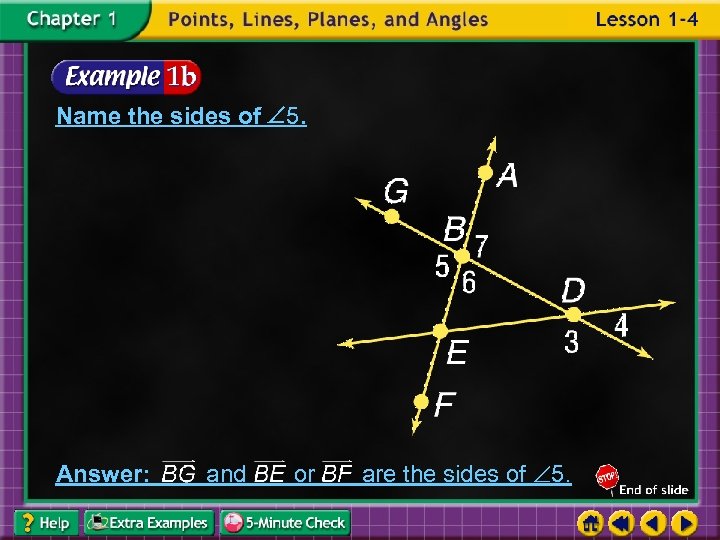
Name the sides of 5. Answer: and or are the sides of 5.

Write another name for 6. Answer: EBD, FBD, DBF, and DBE are other names for 6.
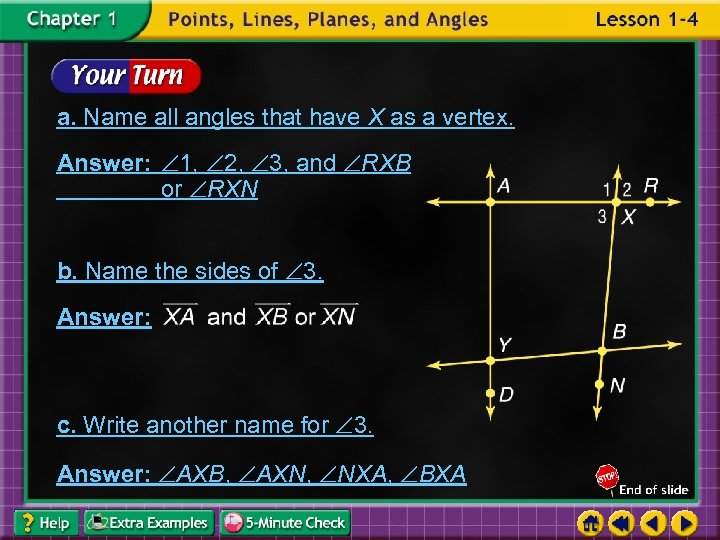
a. Name all angles that have X as a vertex. Answer: 1, 2, 3, and RXB or RXN b. Name the sides of 3. Answer: c. Write another name for 3. Answer: AXB, AXN, NXA, BXA
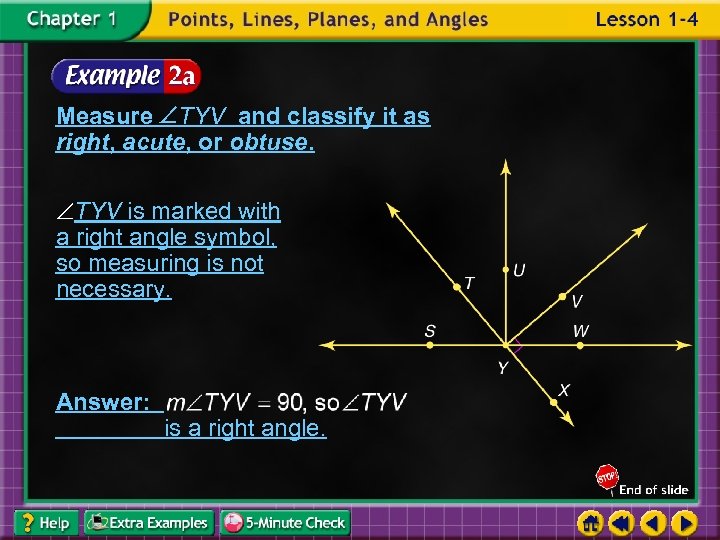
Measure TYV and classify it as right, acute, or obtuse. TYV is marked with a right angle symbol, so measuring is not necessary. Answer: is a right angle.
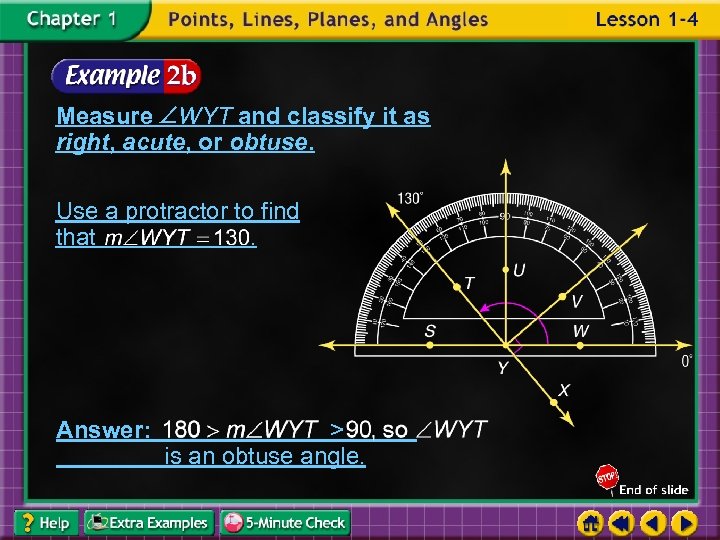
Measure WYT and classify it as right, acute, or obtuse. Use a protractor to find that. Answer: > is an obtuse angle.
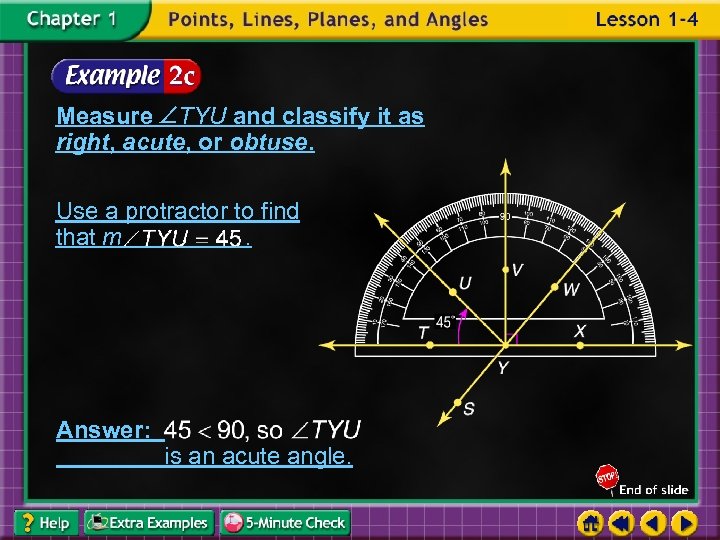
Measure TYU and classify it as right, acute, or obtuse. Use a protractor to find that m. Answer: is an acute angle.
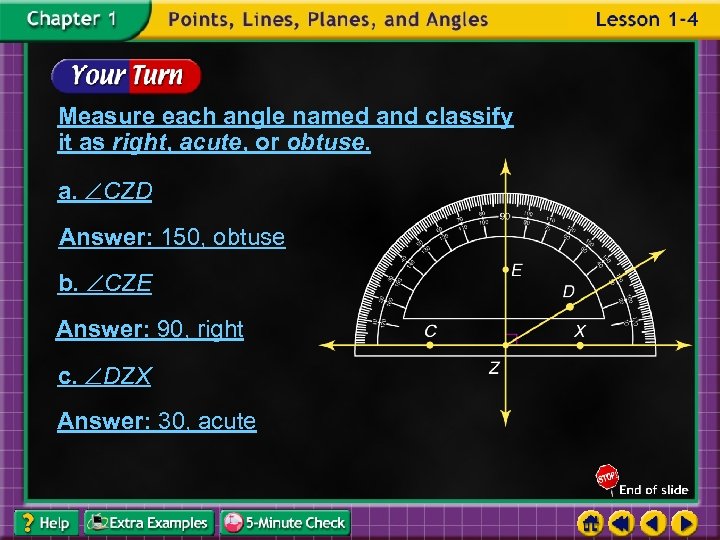
Measure each angle named and classify it as right, acute, or obtuse. a. CZD Answer: 150, obtuse b. CZE Answer: 90, right c. DZX Answer: 30, acute

INTERIOR DESIGN Wall stickers of standard shapes are often used to provide a stimulating environment for a young child’s room. A five-pointed star sticker is shown with vertices labeled. Find m GBH and m HCI if GBH HCI, m GBH 2 x + 5, and m HCI 3 x – 10.
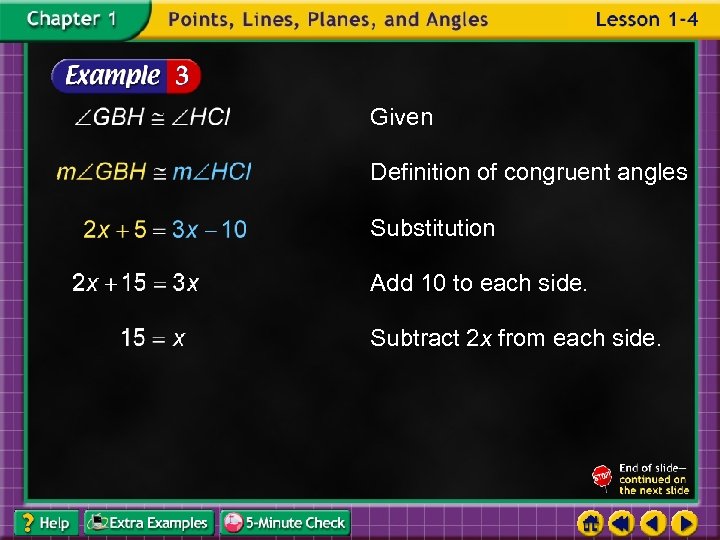
Given Definition of congruent angles Substitution Add 10 to each side. Subtract 2 x from each side.
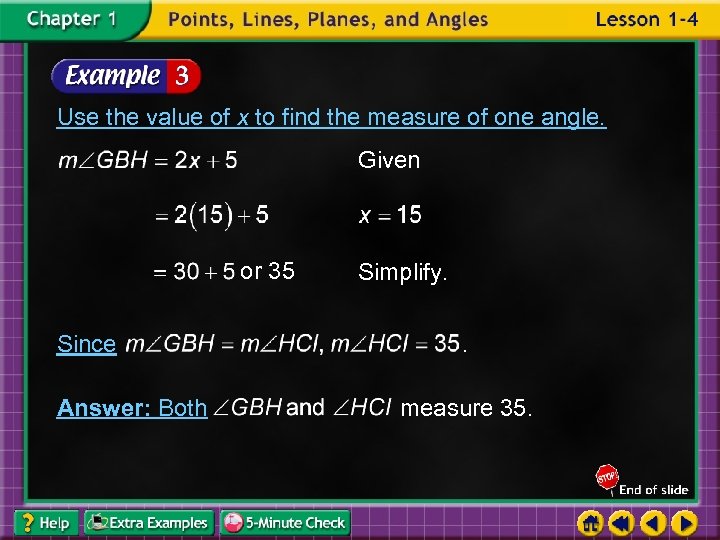
Use the value of x to find the measure of one angle. Given or 35 Since Answer: Both Simplify. . measure 35.

SIGNS A railroad crossing sign forms congruent angles. In the figure, WVX ZVY. If m WVX 7 a + 13 and m ZVY 10 a – 20, find the actual measurements of WVX and ZVY. Answer:


Example 1 Identify Angle Pairs Example 2 Angle Measure Example 3 Perpendicular Lines Example 4 Interpret Figures

Name two angles that form a linear pair. A linear pair is a pair of adjacent angles whose noncommon sides are opposite rays. Answer: The angle pairs that satisfy this definition are
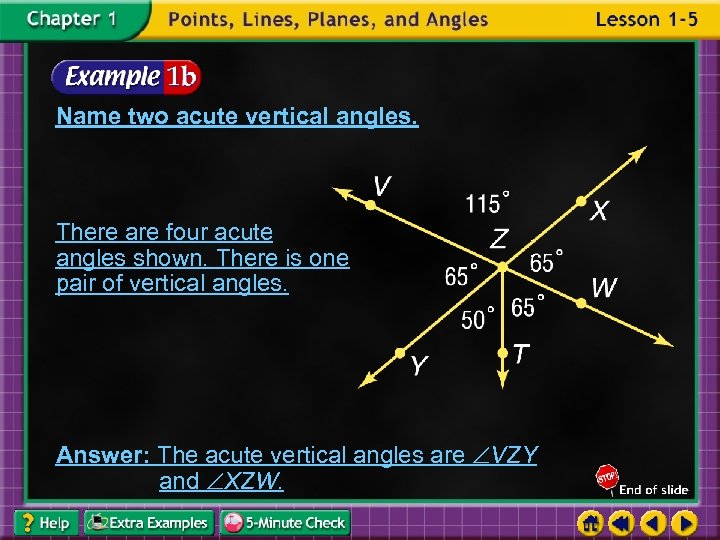
Name two acute vertical angles. There are four acute angles shown. There is one pair of vertical angles. Answer: The acute vertical angles are VZY and XZW.

Name an angle pair that satisfies each condition. a. two acute vertical angles Answer: BAC and FAE, CAD and NAF, or BAD and NAE b. two adjacent angles whose sum is less than 90 Answer: BAC and CAD or EAF and FAN

ALGEBRA Find the measures of two supplementary angles if the measure of one angle is 6 less than five times the other angle. Explore The problem relates the measures of two supplementary angles. You know that the sum of the measures of supplementary angles is 180. Plan Draw two figures to represent the angles.

Let the measure of one angle be x. Solve Given Simplify. Add 6 to each side. Divide each side by 6.

Use the value of x to find each angle measure. Examine Add the angle measures to verify that the angles are supplementary. Answer: 31, 149

ALGEBRA Find the measures of two complementary angles if one angle measures six degrees less than five times the measure of the other. Answer: 16, 74
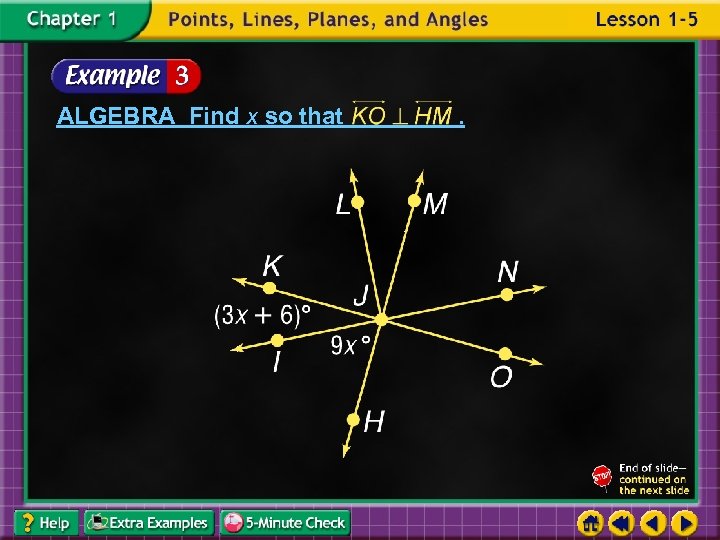
ALGEBRA Find x so that .

If IJH. , then m KJH 90. To find x, use KJI and Sum of parts whole Substitution Add. Subtract 6 from each side. Divide each side by 12. Answer:

ALGEBRA Find x and y so that are perpendicular. Answer: and

Determine whether the following statement can be assumed from the figure below. Explain. m VYT 90 The diagram is marked to show that From the definition of perpendicular, perpendicular lines intersect to form congruent adjacent angles. Answer: Yes; and are perpendicular.
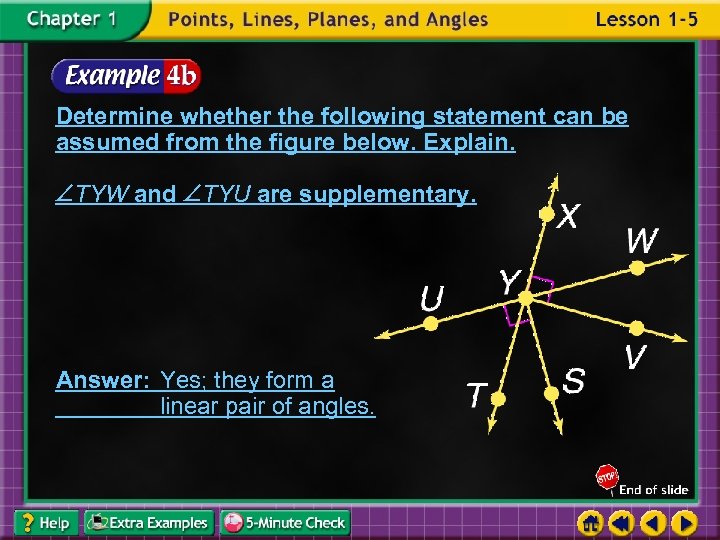
Determine whether the following statement can be assumed from the figure below. Explain. TYW and TYU are supplementary. Answer: Yes; they form a linear pair of angles.
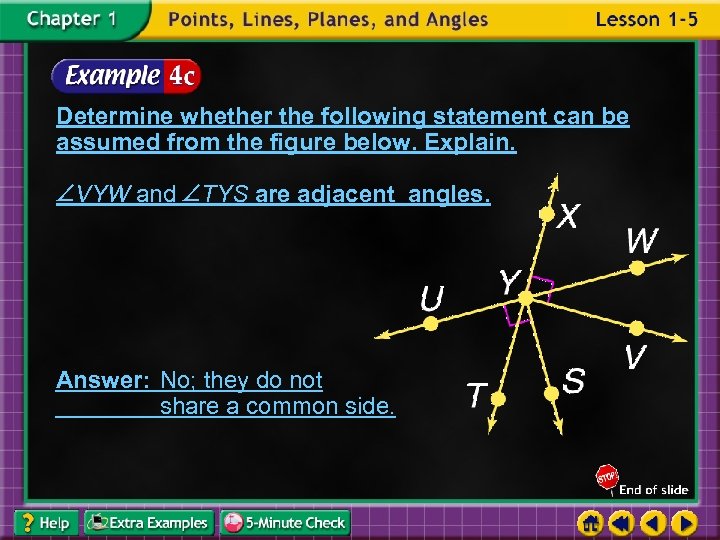
Determine whether the following statement can be assumed from the figure below. Explain. VYW and TYS are adjacent angles. Answer: No; they do not share a common side.

Determine whether each statement can be assumed from the figure below. Explain. a. Answer: Yes; lines TY and SX are perpendicular. b. TAU and UAY are complementary. Answer: No; the sum of the two angles is 180, not 90. c. UAX and UXA are adjacent. Answer: No; they do not share a common side.

Example 1 Identify Polygons Example 2 Find Perimeter Example 3 Perimeter on the Coordinate Plane Example 4 Use Perimeter to Find Sides

Name the polygon by its number of sides. Then classify it as convex or concave, regular or irregular. There are 4 sides, so this is a quadrilateral. No line containing any of the sides will pass through the interior of the quadrilateral, so it is convex. The sides are not congruent, so it is irregular. Answer: quadrilateral, convex, irregular
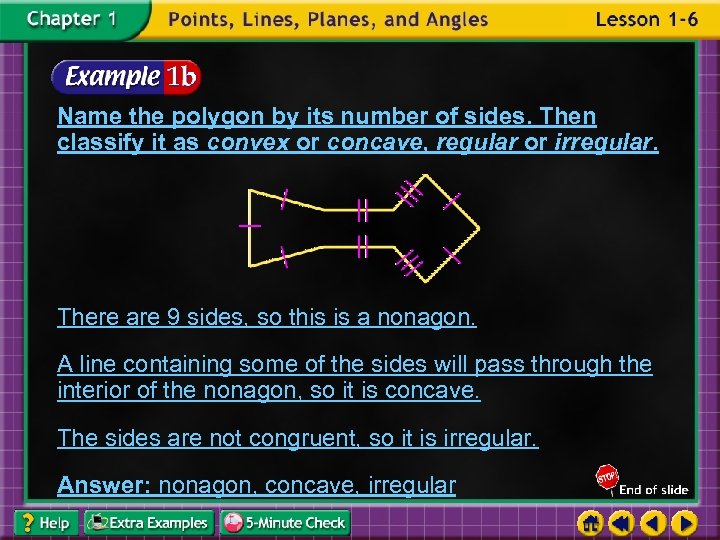
Name the polygon by its number of sides. Then classify it as convex or concave, regular or irregular. There are 9 sides, so this is a nonagon. A line containing some of the sides will pass through the interior of the nonagon, so it is concave. The sides are not congruent, so it is irregular. Answer: nonagon, concave, irregular

Name each polygon by the number of sides. Then classify it as convex or concave, regular or irregular. a. Answer: triangle, convex, regular b. Answer: quadrilateral, convex, irregular
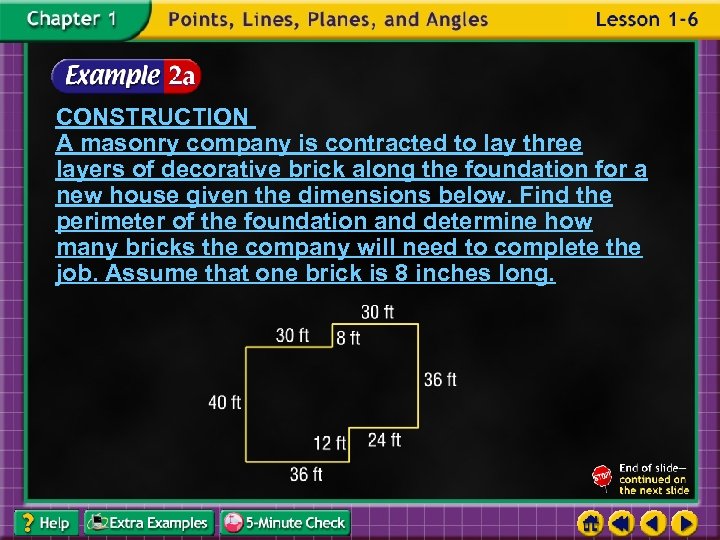
CONSTRUCTION A masonry company is contracted to lay three layers of decorative brick along the foundation for a new house given the dimensions below. Find the perimeter of the foundation and determine how many bricks the company will need to complete the job. Assume that one brick is 8 inches long.

First, find the perimeter. Add the lengths of the sides. The perimeter of the foundation is 216 feet.

Next, determine how many bricks will be needed to complete the job. Each brick measures 8 inches, or Divide 216 by foot. to find the number of bricks needed for one layer. Answer: The builder will need 324 bricks for each layer. Three layers of bricks are needed, so the builder needs 324 • 3 or 972 bricks.

CONSTRUCTION The builder realizes he accidentally halved the size of the foundation in part a. How will this affect the perimeter of the house and the number of bricks the masonry company needs?

The new dimensions are twice the measures of the original lengths. The perimeter has doubled. The new number of bricks needed for one layer is or 648. For three layers, the total number of bricks is 648 • 3 or 1944 bricks. Answer: The perimeter and the number of bricks needed are doubled.
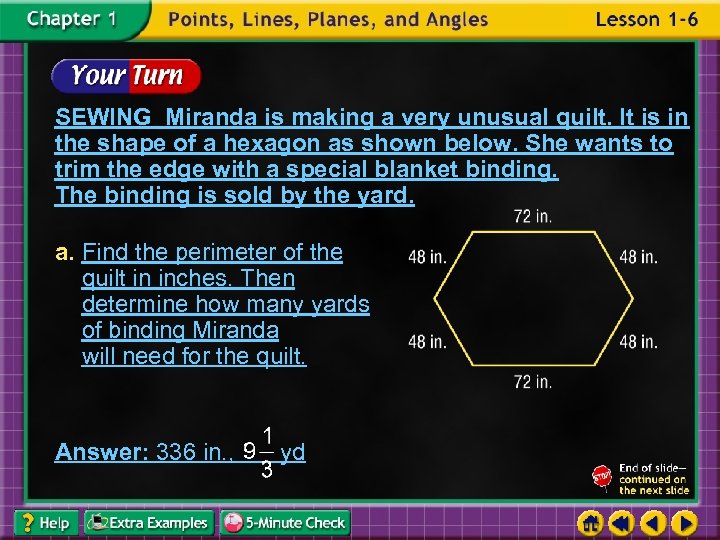
SEWING Miranda is making a very unusual quilt. It is in the shape of a hexagon as shown below. She wants to trim the edge with a special blanket binding. The binding is sold by the yard. a. Find the perimeter of the quilt in inches. Then determine how many yards of binding Miranda will need for the quilt. Answer: 336 in. , yd

SEWING Miranda is making a very unusual quilt. It is in the shape of a hexagon as shown below. She wants to trim the edge with a special blanket binding. The binding is sold by the yard. b. Miranda decides to make four quilts. How will this affect the amount of binding she will need? How much binding will she need for this project? Answer: The amount of binding is multiplied by 4. She will need yards.
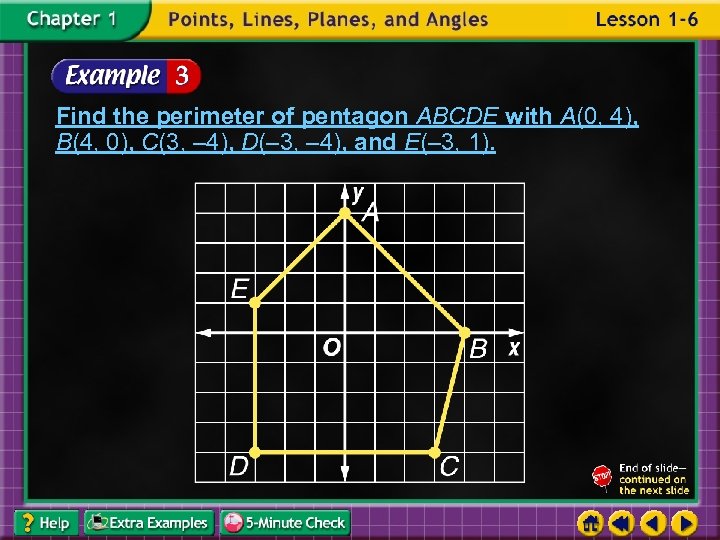
Find the perimeter of pentagon ABCDE with A(0, 4), B(4, 0), C(3, – 4), D(– 3, – 4), and E(– 3, 1).
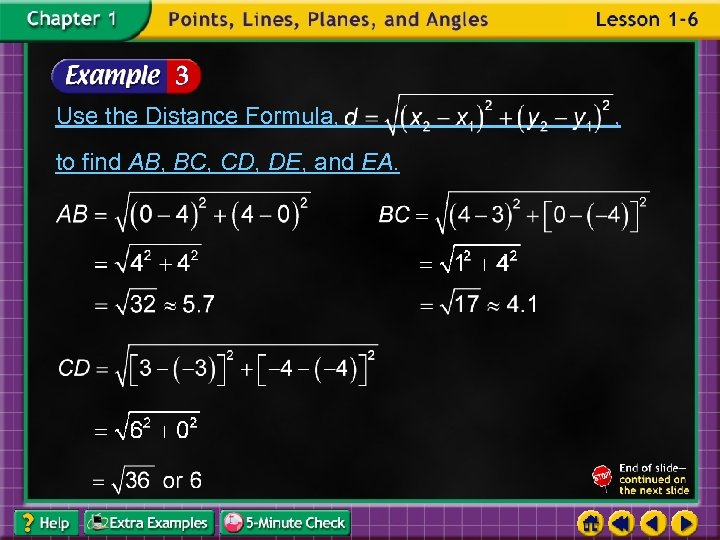
Use the Distance Formula, to find AB, BC, CD, DE, and EA. ,
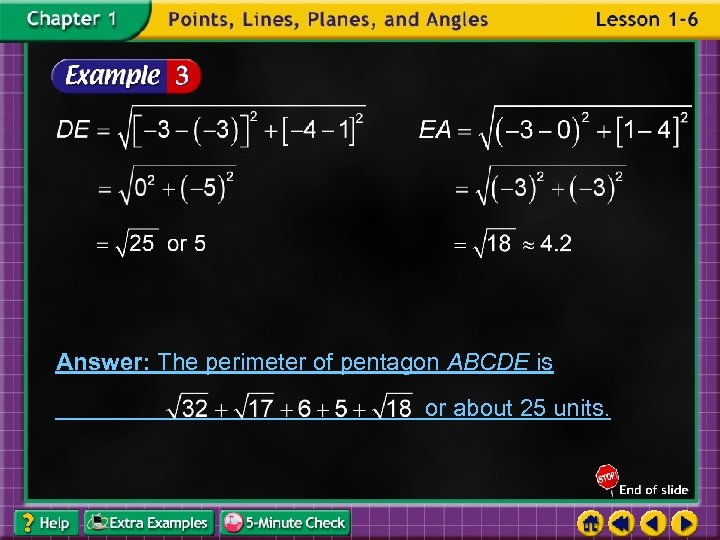
Answer: The perimeter of pentagon ABCDE is or about 25 units.

Find the perimeter of quadrilateral WXYZ with W(2, 4), X(– 3, 3), Y(– 1, 0), and Z(3, – 1). Answer: about 17. 9 units
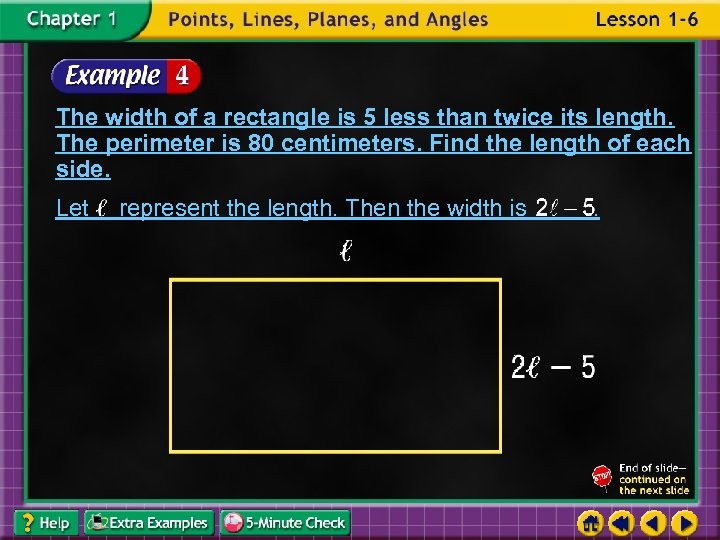
The width of a rectangle is 5 less than twice its length. The perimeter is 80 centimeters. Find the length of each side. Let represent the length. Then the width is .

Perimeter formula for rectangle Multiply. Simplify. Add 10 to each side. Divide each side by 6. The length is 15 cm. By substituting 15 for , the width becomes 2(15) – 5 or 25 cm. Answer:

The length of a rectangle is 7 more than five times its width. The perimeter is 134 feet. Find the length of each side. Answer:


Explore online information about the information introduced in this chapter. Click on the Connect button to launch your browser and go to the Glencoe Geometry Web site. At this site, you will find extra examples for each lesson in the Student Edition of your textbook. When you finish exploring, exit the browser program to return to this presentation. If you experience difficulty connecting to the Web site, manually launch your Web browser and go to www. geometryonline. com/extra_examples.

Click the mouse button or press the Space Bar to display the answers.

Click the mouse button or press the Space Bar to display the answers.
Click the mouse button or press the Space Bar to display the answers.


Click the mouse button or press the Space Bar to display the answers.


Click the mouse button or press the Space Bar to display the answers.

Click the mouse button or press the Space Bar to display the answers.


End of Custom Shows WARNING! Do Not Remove This slide is intentionally blank and is set to auto-advance to end custom shows and return to the main presentation.

fd0b245685e3b660ee48ef9d3bc34369.ppt