fa9fd0340279a098e24b308b88db053f.ppt
- Количество слайдов: 39

Главная Астрономическая Обсерватория РАН Санкт-Петербург Н. Г. МАКАРЕНКО ГЕОМЕТРИЯ И ТОПОЛОГИЯ ФИЗИЧЕСКИХ ПОЛЕЙ ИЗ АСТРОНОМИЧЕСКИХ ЦИФРОВЫХ ИЗОБРАЖЕНИЙ «Физика плазмы в солнечной системе» 14 - 18 февраля 2011 г. ИКИ РАН

ЧТО МЫ МОЖЕМ ИЗМЕРИТЬ?
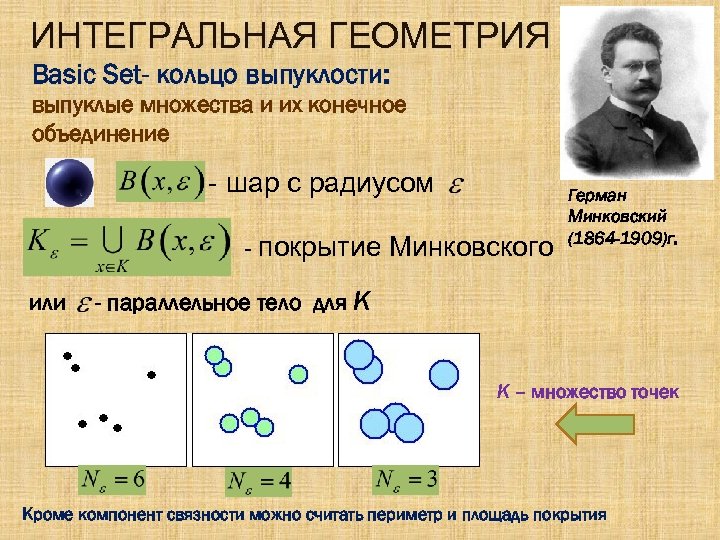
ИНТЕГРАЛЬНАЯ ГЕОМЕТРИЯ Basic Set- кольцо выпуклости: выпуклые множества и их конечное объединение - шар с радиусом - покрытие Минковского или Герман Минковский (1864 -1909)г. - параллельное тело для K K – множество точек Кроме компонент связности можно считать периметр и площадь покрытия

ФОРМУЛА ШТЕЙНЕРА В Функционалы Минковского Якоб Штейнер (1796 -1863)г. =1 = =0 + -- =1+1 -1=1 K

Морфологические свойства Г. Хадвигер. Лекции об объеме, площади поверхности и изопериметрии, 1966 Хьюго Хадвигер 1908 -1981 г.
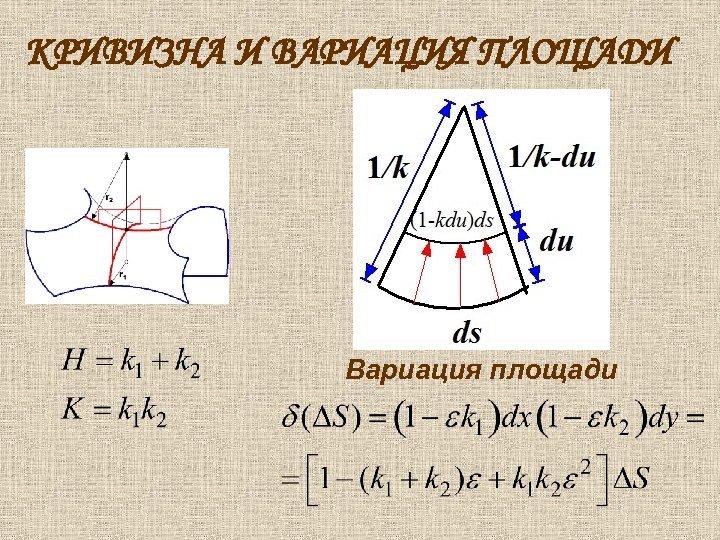
КРИВИЗНА И ВАРИАЦИЯ ПЛОЩАДИ Вариация площади

TUBE FORMULA Герман Вейль (1885 -1955) - Кривизна Липшица - Киллинга - Функционалы Минковского
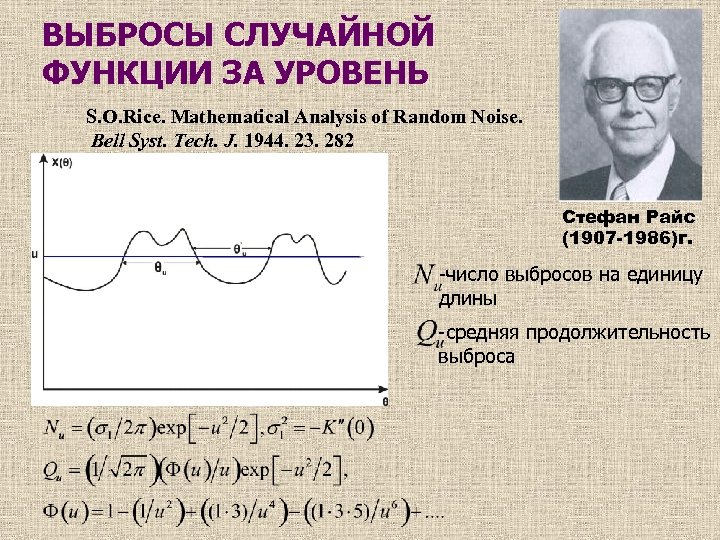
ВЫБРОСЫ СЛУЧАЙНОЙ ФУНКЦИИ ЗА УРОВЕНЬ S. O. Rice. Mathematical Analysis of Random Noise. Bell Syst. Tech. J. 1944. 23. 282 Стефан Райс (1907 -1986)г. -число выбросов на единицу длины -средняя продолжительность выброса

R. Adler The Geometry of Random Fields. K. J. Worsley, The geometry of random Images. Chance. 1996. 9(1). 27 Robert Аdler Technion-Israel Institute of Technology Для достаточно регулярного случайного поля, множество выбросов принадлежит кольцу выпуклости ВСЕ ФУНКЦИИ И МНОЖЕСТВА – РУЧНЫЕ ВСЕ МНОГООБРАЗИЯ- СТРАТИФИЦИРОВАННЫЕ Keit Worsley Mc. Gill University, Canada

ЧТО ТАКОЕ ИЗОБРАЖЕНИЕ? Истинных изображений не существует! Это всего лишь отклик сенсора! Слабое дифференцирование:
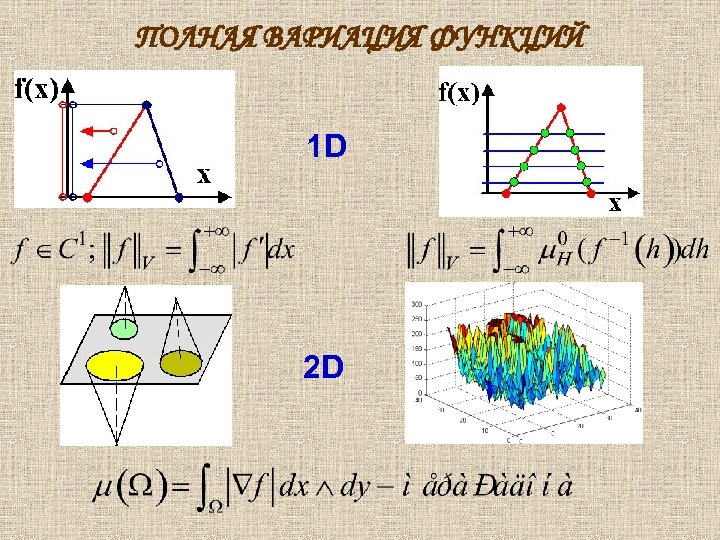
ПОЛНАЯ ВАРИАЦИЯ ФУНКЦИЙ 1 D 2 D
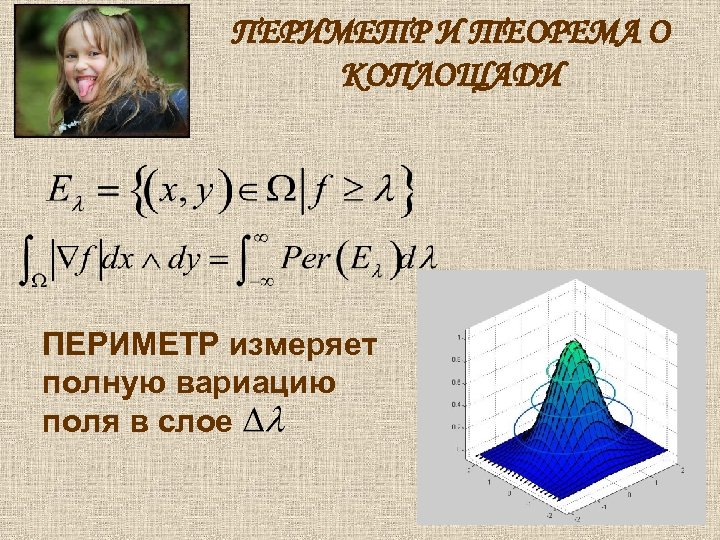
ПЕРИМЕТР И ТЕОРЕМА О КОПЛОЩАДИ ПЕРИМЕТР измеряет полную вариацию поля в слое

ХАРАКТЕРИСТИКА ЭЙЛЕРА Леонард Эйлер (1707 -1783) +1 -1

И ТЕОРИЯ МОРСА

РЕЗУЛЬТАТЫ АНАЛИЗА MDI 1. Сложность поля - Эйлерова характеристика 2. Вариация градиента - Периметр
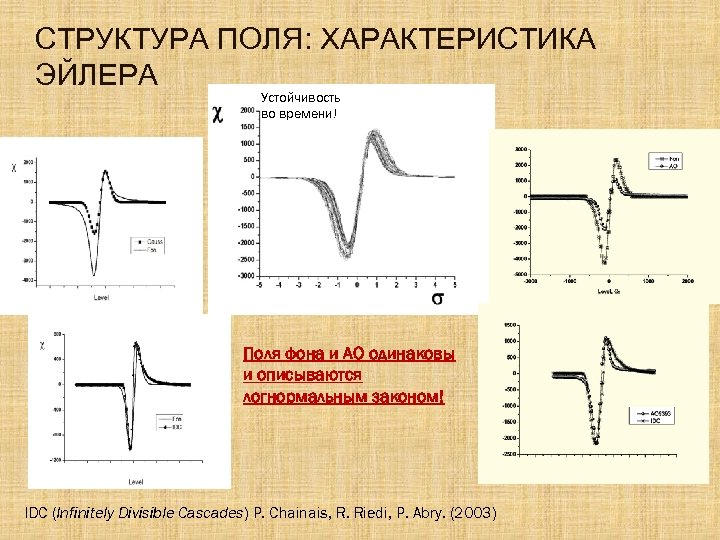
СТРУКТУРА ПОЛЯ: ХАРАКТЕРИСТИКА ЭЙЛЕРА Устойчивость во времени! Поля фона и АО одинаковы и описываются логнормальным законом! IDC (Infinitely Divisible Cascades) P. Chainais, R. Riedi, P. Abry. (2003)
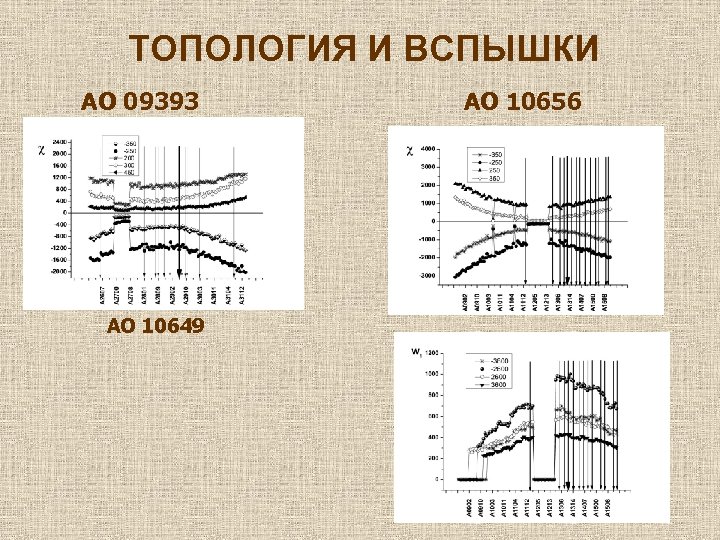
ТОПОЛОГИЯ И ВСПЫШКИ AO 09393 AO 10649 AO 10656
ФОРМЫ НА ОБЛАКЕ ТОЧЕК Имеется облако точек из неизвестного топологического многообразия Х. Как реконструировать Х с точностью до гомологий ?
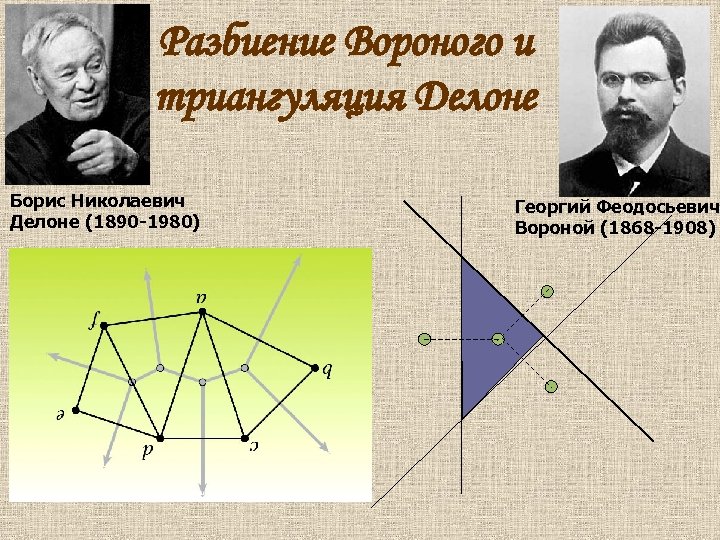
Разбиение Вороного и триангуляция Делоне Борис Николаевич Делоне (1890 -1980) Георгий Феодосьевич Вороной (1868 -1908)
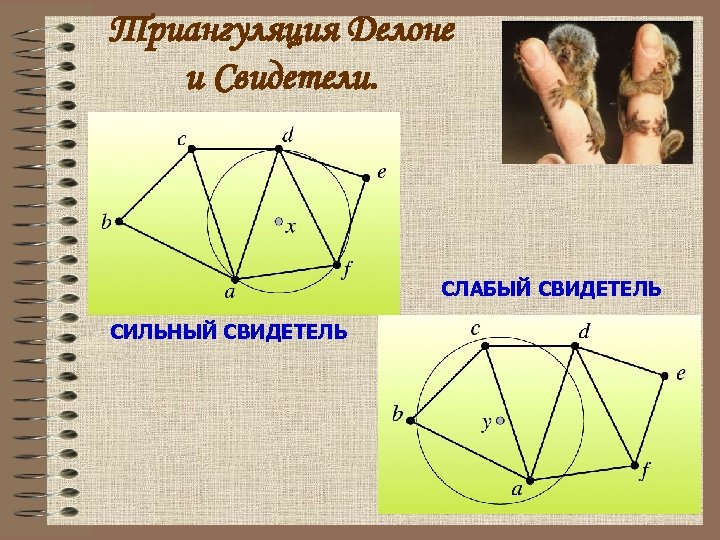
Триангуляция Делоне и Свидетели. СЛАБЫЙ СВИДЕТЕЛЬ СИЛЬНЫЙ СВИДЕТЕЛЬ

КОМПЛЕКСЫ ЧЕХА –ВЬЕТОРИСА-РИПСА Вьеторис Леопольд Франц (1891 -2002) Илья Рипс (1948 -) Эдуард Чех (1893 -1960)
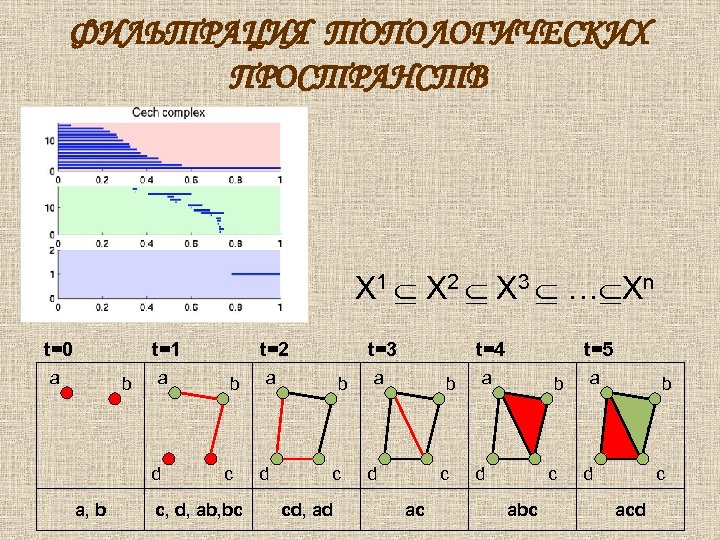
ФИЛЬТРАЦИЯ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ X 1 X 2 X 3 … Xn t=0 t=1 a b a d a, b t=2 b c c, d, ab, bc t=3 a d b c cd, ad t=4 a b d c ac t=5 a b d c abc a b d c acd
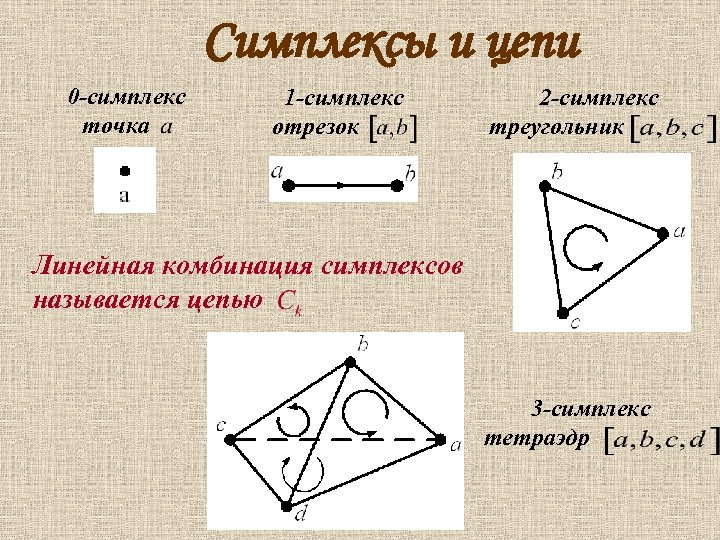
Симплексы и цепи 0 -симплекс точка 1 -симплекс отрезок 2 -симплекс треугольник Линейная комбинация симплексов называется цепью 3 -симплекс тетраэдр

ОПЕРАТОР ГРАНИЦЫ Граница границы есть нуль!
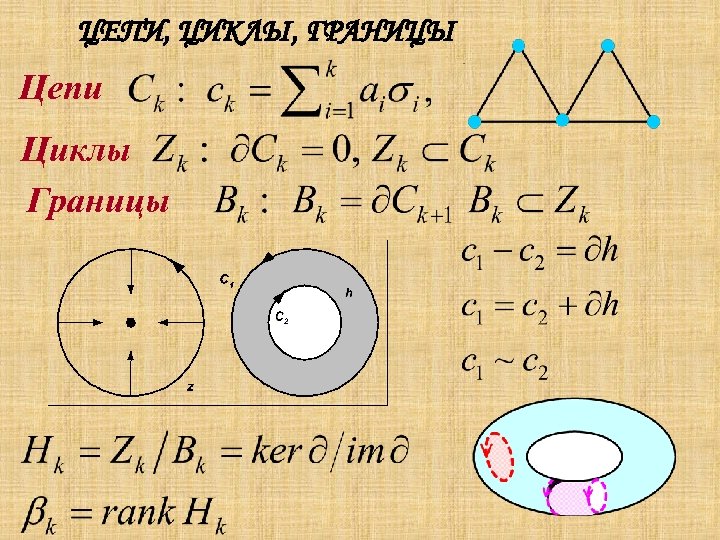
ЦЕПИ, ЦИКЛЫ, ГРАНИЦЫ Цепи Циклы Границы

Гомологии Сферы Векторное поле на сфере имеет 2 особенности
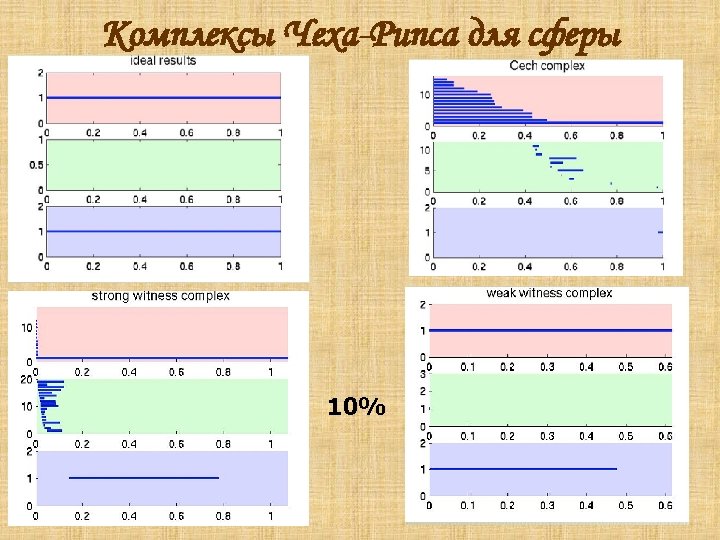
Комплексы Чеха-Рипса для сферы 10%
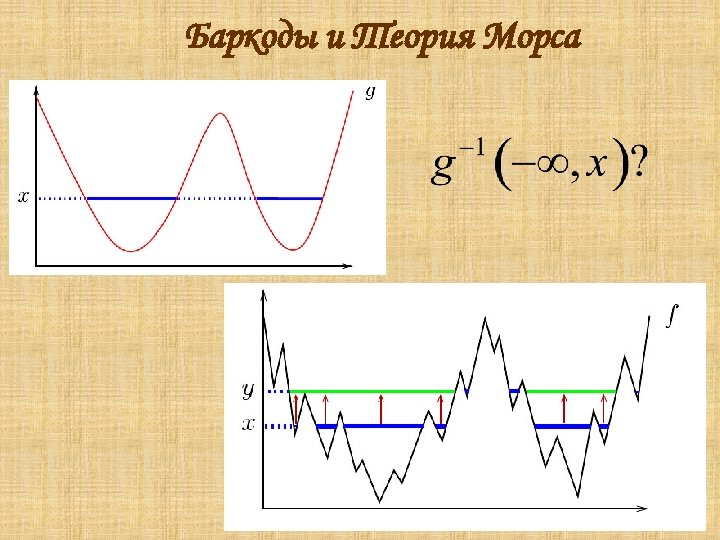
Баркоды и Теория Морса
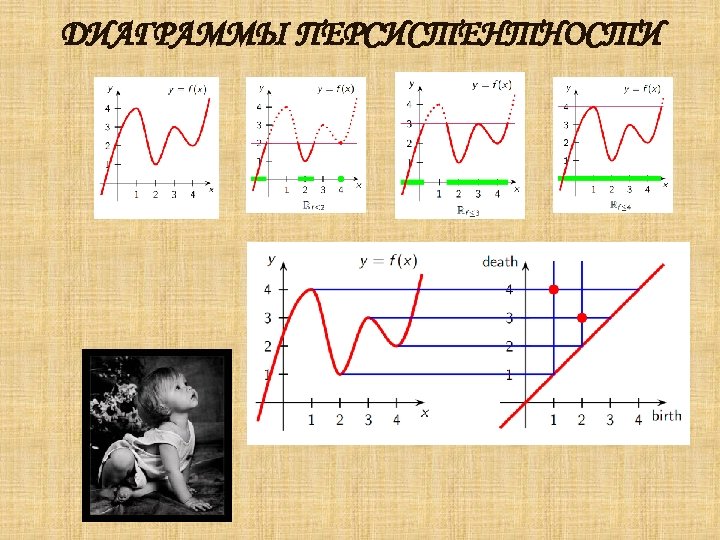
ДИАГРАММЫ ПЕРСИСТЕНТНОСТИ
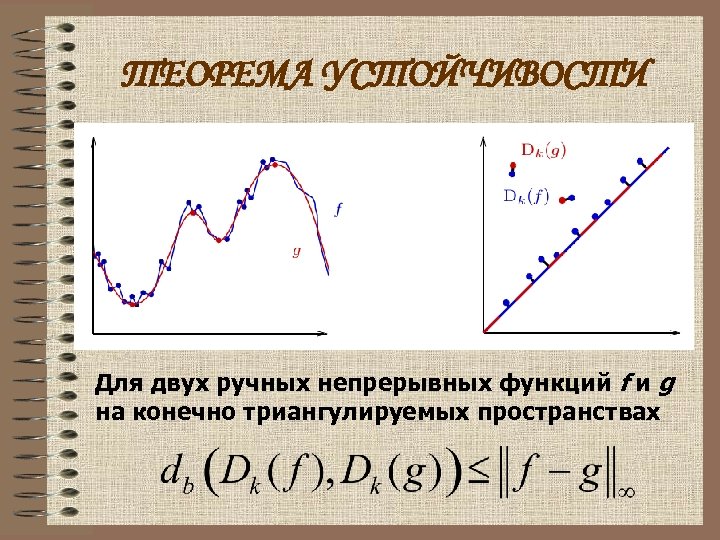
ТЕОРЕМА УСТОЙЧИВОСТИ Для двух ручных непрерывных функций f и g на конечно триангулируемых пространствах
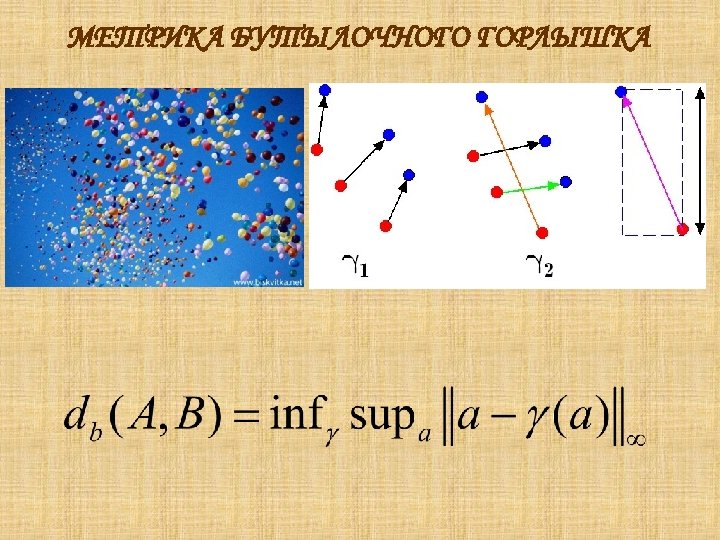
МЕТРИКА БУТЫЛОЧНОГО ГОРЛЫШКА
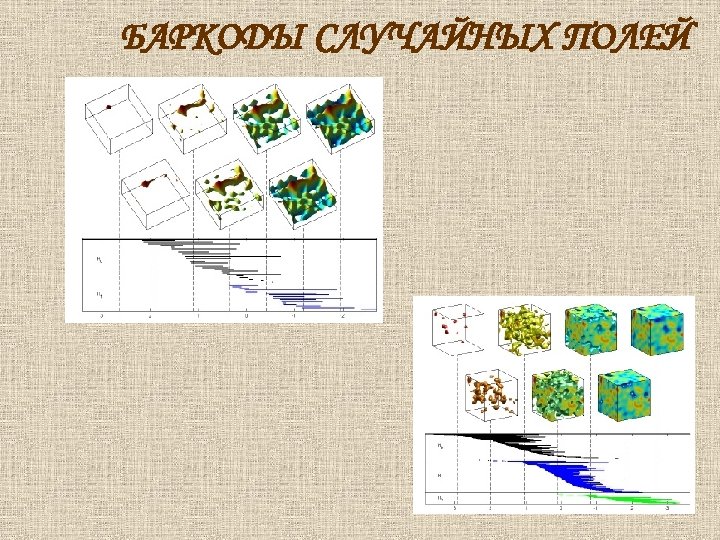
БАРКОДЫ СЛУЧАЙНЫХ ПОЛЕЙ
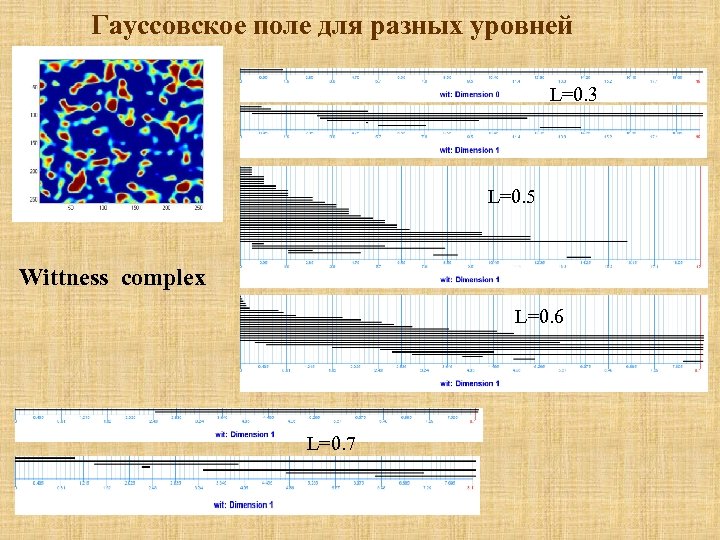
Гауссовское поле для разных уровней L=0. 3 L=0. 5 Wittness complex L=0. 6 L=0. 7
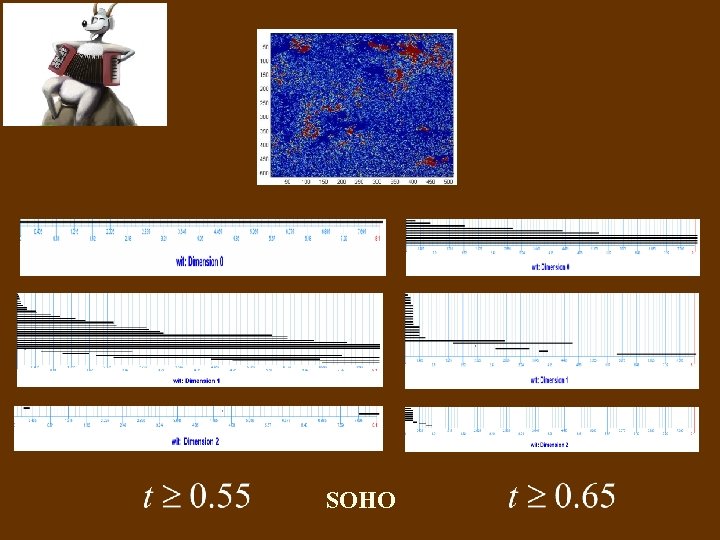
SOHO
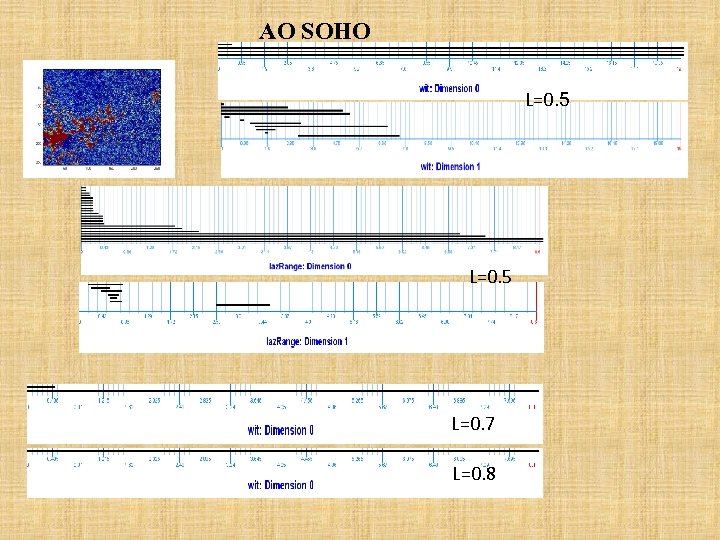
АО SOHO L=0. 5 L=0. 7 L=0. 8
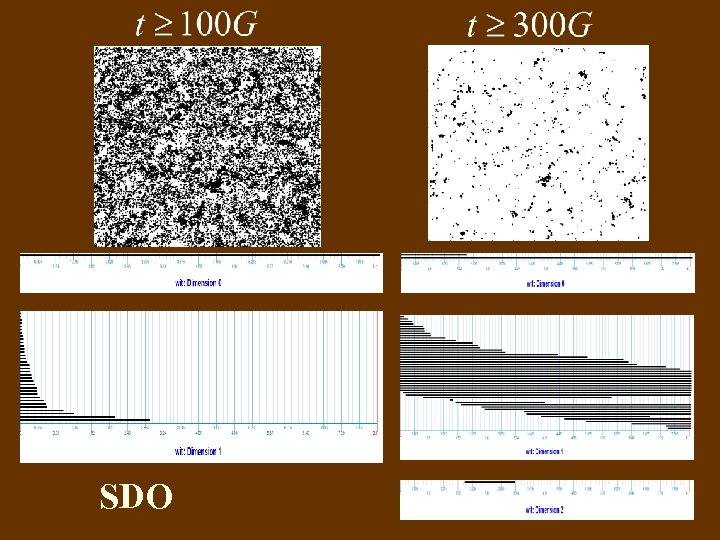
SDO

КАК УСЛЫШАТЬ 3 D ГЕОМЕТРИЮ ПОЛЯ мера грубости поля

ВОССТАНОВЛЕНИЕ ТОПОЛОГИИ ПОЛЯ С ТОЧНОСТЬЮ ДО ГОМОЛОГИЙ ? ? Лозы и Виноградники Дискретные гомотопии (B. T. Fazy (2010)//ar. Xiv 1002. 1937 v. 1)

СПАСИБО ЗА ВНИМАНИЕ!
fa9fd0340279a098e24b308b88db053f.ppt