Глава 5 Теория точности измерений Глава 5

Глава 5. Теория точности измерений

Глава 5. Теория точности измерений Основная задача: оценка степени приближения результата измерения к истинному значению измеряемой величины - X.

Теория точности ТЕОРИЯ ТОЧНОСТИ АПРИОРИ ТЕОРИЮ ТОЧНОСТИ АПОСТЕРИОРИ содержанием которой является анализ погрешностей средств измерения в статике и динамике, методы повышения точности средств измерений. Основной целью является оценивание и снижение погрешности каждого т. е. теорию точности оценивания результата измерений, содержанием которой является анализ погрешностей измерения, методы обработки результатов многократных наблюдений, повышающих точность результата измерений. Основной целью является оценивание и снижение погрешности конечного результата измерений. отдельного результата наблюдения.

ОБЩИЕ ПРИНЦИПЫ повышения точности измерений 1. При преобладании случайной составляющей погрешности общим принципом повышения точности измерений является усреднение. 2. При преобладании систематических и относительно медленно изменяющихся случайных погрешностей принципами повышения точности измерений являются: a. b. c. предотвращение возникновения погрешностей в средствах измерений конструктивно-технологическими и защитнопредохранительными методами; выявление существующих погрешностей и преобразование их в воздействие, компенсирующее выявленную погрешность, на основе образцовых прямых и обратных измерительных преобразователей и мер; функциональная обработка результатов измерений, выполненных по специальной методике с целью уменьшения погрешностей.

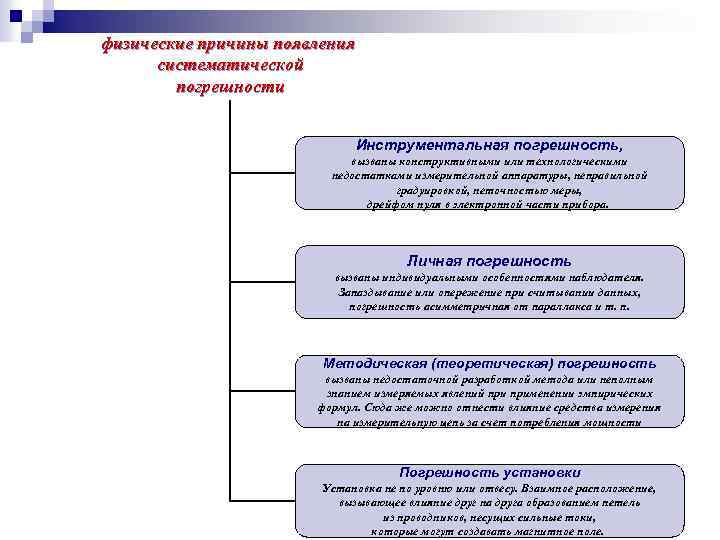физические причины появления систематической погрешности Инструментальная погрешность, вызваны конструктивными или технологическими недостатками измерительной аппаратуры, неправильной градуировкой, неточностью меры, дрейфом нуля в электронной части прибора. Личная погрешность вызваны индивидуальными особенностями наблюдателя. Запаздывание или опережение при считывании данных, погрешность асимметричная от параллакса и т. п. Методическая (теоретическая) погрешность вызваны недостаточной разработкой метода или неполным знанием измеряемых явлений применении эмпирических формул. Сюда же можно отнести влияние средства измерения на измерительную цепь за счет потребления мощности Погрешность установки Установка не по уровню или отвесу. Взаимное расположение, вызывающее влияние друг на друга образованием петель из проводников, несущих сильные токи, которые могут создавать магнитное поле.

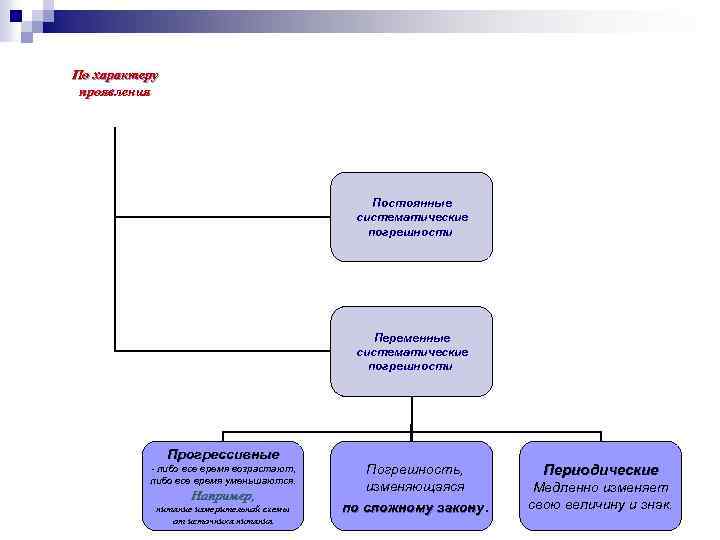По характеру проявления Постоянные систематические погрешности Переменные систематические погрешности Прогрессивные - либо все время возрастают, либо все время уменьшаются. Например, питание измерительной схемы от источника питания Погрешность, изменяющаяся по сложному закону. Периодические Медленно изменяет свою величину и знак.

5. 1 Влияние систематических погрешностей на результат измерения Постановка задачи: Пусть провели избыточные измерения и их результаты загрязнены систематической погрешностью. Обозначим n x 1, x 2, …, xn – неисправленные значения отдельных измерений, которые содержат систематические погрешности; n l 1, l 2, …, ln – исправленные значения, из которых систематические погрешности исключены. 1) Ограничимся тремя составляющими постоянных систематических погрешностей: ’ =const, ’’’ =const.

Тогда можно записать: (1) (2) где (3) Величины – ’, – ’’’ называются поправками

ПОПРАВКА – это значение величины, одноименной с измеряемой, которое алгебраически суммируется со значением величины, полученным при измерении, с целью исключения систематической погрешности (её прибавляют к неисправленному значению, чтобы получить исправленное).

Обозначим поправки (4) Если систематические погрешности постоянные, то исключение их в среднеарифметическом происходит точно так же, как и в отдельном измерении: Введем величину: (5) (6) Это остаточная погрешность. Подставим в (6) выражения (1) и (3): (7) (8)

Вывод: постоянные систематические погрешности не могут быть обнаружены при обработке одной группы результатов измерений.

2) Предположим что погрешности ’ =var, ’’’ =var содержат только переменные систематические составляющие. (9) (10) Поправки (11)

остаточная погрешность: (12) (13) (14) Обозначив: (15)

Вывод: Вместе с тем здесь появляется возможность обнаружить переменные систематические погрешности при обработке одной группы измерений.

5. 2 Обнаружение систематических погрешностей Из выражения (15): (16) Если случайные погрешности малы, то знаки погрешностей второй составляющей будут определять знаки погрешностей i’.

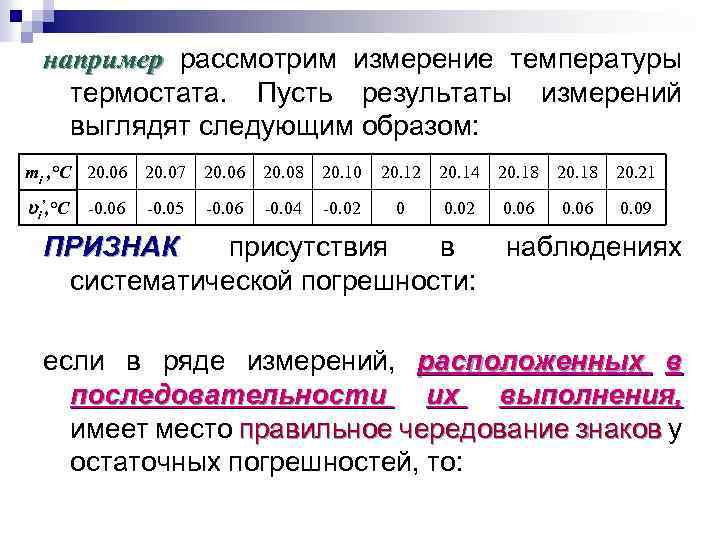например рассмотрим измерение температуры термостата. Пусть результаты измерений выглядят следующим образом: mi , °С 20. 06 20. 07 20. 06 20. 08 20. 10 20. 12 20. 14 20. 18 20. 21 i’, °С -0. 05 -0. 06 -0. 04 -0. 02 0. 06 0. 09 -0. 06 ПРИЗНАК присутствия в систематической погрешности: наблюдениях если в ряде измерений, расположенных в последовательности их выполнения, имеет место правильное чередование знаков у остаточных погрешностей, то:

n ряд содержит ПРОГРЕССИВНУЮ СИСТЕМАТИЧЕСКУЮПОГРЕШНОСТЬ если последовательность знаков «+» сменяется последовательностью знаков «–» или наоборот; n ряд содержит ПЕРИОДИЧЕСКУЮ СИСТЕМАТИЧЕСКУЮ ПОГРЕШНОСТЬ, если последовательности знаков «+» и « – » закономерно чередуются.

КРИТЕРИЙ для систематической (Критерий Маликова). обнаружения погрешности Сложим отдельно k первых и k последних по порядку остаточных погрешностей, принимая при п четном и при п нечетном, и вычтем одну сумму из другой. (17)

КРИТЕРИЙ Если разность сумм остаточных погрешностей для первой и второй половины ряда, состоящего из не очень малого числа измерений, заметно отличается от нуля ( превышает по абсолютной величине максимальную остаточную погрешность), то данный прогрессивную погрешность. ряд содержит систематическую

Применим этот критерий для данных таблицы: ряд результатов наблюдений содержит монотонно изменяющуюся систематическую погрешность

Предположим, что систематическая погрешность изменяется по линейному закону, тогда: t+ 0=20. 06 t+ 0+ =20. 07 t+ 0+2 =20. 06 t+ 0+3 =20. 08 t+ 0+4 =20. 10 t+ 0+5 =20. 12 t+ 0+6 =20. 14 t+ 0+7 =20. 18 t+ 0+8 =20. 18 t+ 0+9 =20. 21 где t – действительная температура; 0 – постоянной систематической погрешности, соответствующей первому наблюдению; – приращение систематической погрешности от наблюдения к наблюдению.

Обозначим t+ 0=x и =у, получим систему линейных уравнений: 10 х+45 у=201. 2 //сумма всех уравнений. 45 x+285 у=908. 86 //сумма 2 -го*1, 3 -го*, . . . , 10 -го*9 Решение: x= t+ 0= 20, 040 °С; у= = 0, 0177 °С.