презентация_Теория колебаний.ppt
- Количество слайдов: 78

ГЛАВА 5 Теория колебаний Общие понятия Под колебательным процессом принято понимать немонотонное изменение на некотором отрезке времени одного или нескольких параметров динамической системы. ЗАДАЧЕЙ курса ТЕОРИИ КОЛЕБАНИЙ является изучение с единой точки зрения колебательных процессов, встречающихся в разнообразных физических явлениях и технических устройствах.

Классификация колебательных систем: по виду уравнения движения: линейные и нелинейные Линейными называют такие системы, в которых математическое моделирование процесса колебаний описывается линейными дифференциальными уравнениями. Нелинейными называют такие системы, в которых математическое моделирование процесса колебаний описывается нелинейными дифференциальными уравнениями. по числу степеней свободы: Колебательные системы с одной степенью свободы; Колебательные системы с несколькими степенями свободы; Колебательные системы с бесконечным числом степеней свободы. Под числом степеней свободы механической системы понимается количество независимых числовых параметров (координат), однозначно определяющих состояние системы в любой фиксированный момент времени.

по энергетическим затратам: консервативные и неконсервативные Система называется консервативной, если ее полная механическая энергия остается постоянной при колебаниях. В противном случае систему называют неконсервативной. по зависимости от времени: стационарная и нестационарная Если свойства механической системы изменяются во времени, то ее называют нестационарной. В противном случае систему называют стационарной. по взаимодействию с окружающей средой: автономные и неавтономные Систему называют неавтономной, если колебания этой системы происходит вследствие внешних возмущений, величина которых явно зависит от времени. В автономных системах колебания могут происходить лишь за счет внутренней энергии либо энергии, сообщенной в виде начального возмущения. Автономными также называются системы, нагруженные внешними силами, не зависящими явно от времени и определяемыми движениями самой системы.

Классификация колебаний: по форме: периодические, непериодические, почти периодические Периодическим называется такой процесс, при котором значение величины, совершающей колебания, определенное в любой момент времени, повторится через некоторый постоянный промежуток времени T. При математическом моделировании колебательного процесса используется понятие периодической функции. Функция f(t) называется периодической, если существует такая постоянная величина Т, для которой при любом значении t. Непериодическими можно назвать все остальные функции, не удовлетворяющие сформулированному условию периодичности. Почти периодическая функция обладает следующим свойством: uде Т и ε const Величина Т называется почти периодом.
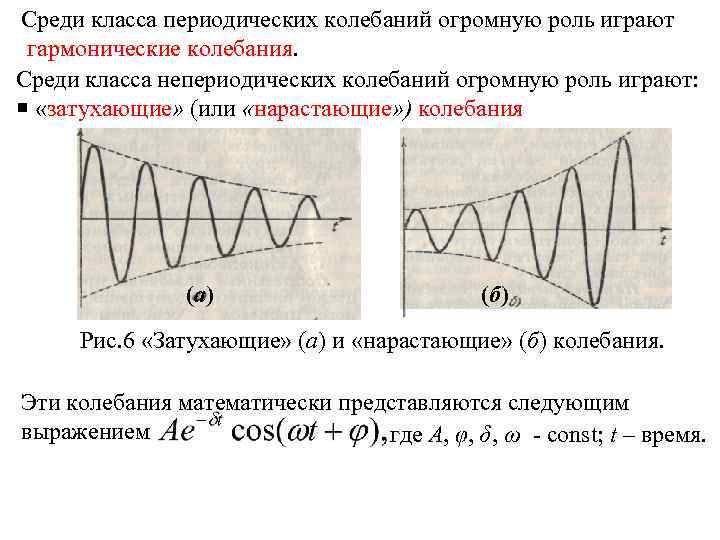
Среди класса периодических колебаний огромную роль играют гармонические колебания. Среди класса непериодических колебаний огромную роль играют: «затухающие» (или «нарастающие» ) колебания (а) (б) Рис. 6 «Затухающие» (а) и «нарастающие» (б) колебания. Эти колебания математически представляются следующим выражением где А, φ, δ, ω const; t – время.
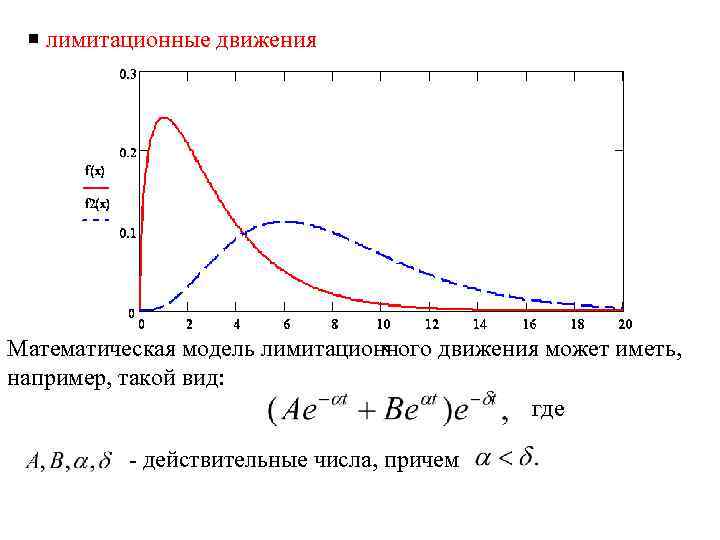
лимитационные движения Математическая модель лимитационного движения может иметь, например, такой вид: где действительные числа, причем

по типу конкретных механических систем: Собственные колебания происходят в изолированной физической автономной системе после внешнего возмущения ( «толчка» ), вызывающего смещение, деформацию или изменение скорости, или изменение других параметров. Характер собственных колебаний, в основном, определяется собственными параметрами системы (геометрическими и массовыми характеристиками, упругостью, емкостью, индуктивностью) и только внутренними силами системы, зависящими от ее физического строения. Необходимая для процесса энергия доставляется извне в начальный момент возбуждения колебаний. Вынужденные колебания происходят в неавтономных системах под действием заданных внешних периодических сил, которые действуют независимо от колебаний в системе. Характер процесса определяется не только свойствами системы, но и существенно зависит от внешней силы. При воздействии периодической силы на систему происходит процесс установления колебаний, длительность которого определяется физическими свойствами системы. Энергия колебаний доставляется в систему источником внешней силы.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы. Характер колебаний определяется исключительно устройством системы.

Введем некоторые другие понятия: Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука): F=-kx, где к положительная константа, описывающая жёсткость системы. Если F единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.
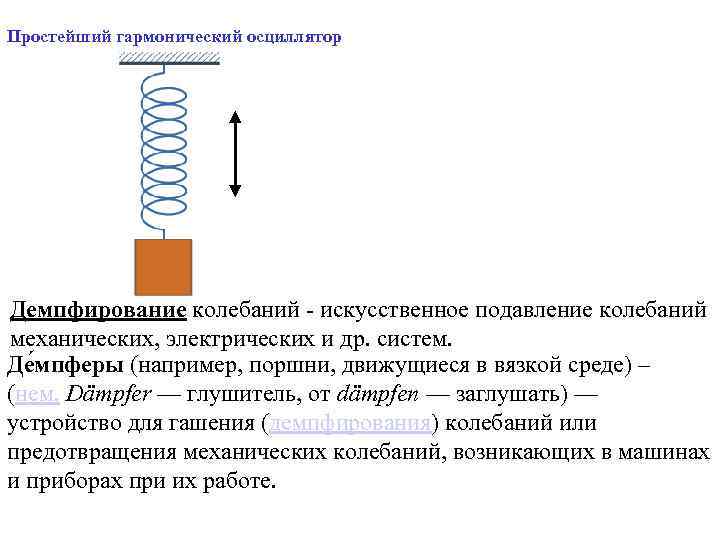
Простейший гармонический осциллятор Демпфирование колебаний искусственное подавление колебаний механических, электрических и др. систем. Де мпферы (например, поршни, движущиеся в вязкой среде) – (нем. Dämpfer — глушитель, от dämpfen — заглушать) — устройство для гашения (демпфирования) колебаний или предотвращения механических колебаний, возникающих в машинах и приборах при их работе.

Резона нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Наиболее известная большинству людей механическая резонансная система — это обычные качели.

Малые колебания системы с одной степенью свободы z M 2 A 1 СОБСТВЕННЫЕ КОЛЕБАНИЯ Представим себе систему, F состоящую из материальных точек 2 Mn F 1 O M 1 A 2 An Fn y x Рис. 8 Предположим, что эта система консервативная и что приложенные силы F 1, F 2 , . . . Fn имеют потенциал. Обобщенную координату системы обозначим через q. Обозначим буквами А 1, А 2, . . . , Аn равновесное положение системы и предположим, что это равновесное положение устойчиво. Если мы нарушим равновесие, придав системе незначительное отклонение от ее равновесного положения, и сообщим точкам системы незначительные начальные скорости и если затем предоставим систему действию приложенных к ней сил F 1, F 2, . . , Fn то в последующем движении каждая точка Мi будет оставаться вблизи своего равновесного положения Аi.

Формулировка задачи: исследовать эти малые колебания системы около ее равновесного положения. Для решения задачи воспользуемся методом Лагранжа. Составим дифференциальное уравнение малых колебаний системы, используя обобщенную координату q. (1) где Т кинетическая энергия; П - потенциальная энергия. Примем, что в положении равновесия q = 0. В дальнейшем будем считать координату q, а также ее производную по времени малыми величинами первого порядка малости. Кинетическая энергия Т, выраженная в обобщенных скоростях и координатах, применительно к нашему случаю системы с одной степенью свободы, запишется в виде: (1 а) где величина А есть функция q

Если за координату q принято перемещение какой либо точки M 0 системы, то обобщенная скорость является линейной скоростью точки М 0. В этом случае величина А и называется массой системы, приведенной к точке М 0. Если же координата q определяет угол поворота вокруг некоторой оси z 0, то величина А называется моментом инерции системы, приведенным к оси z 0. Полагая А(0)=а, выражение (1 а) примет вид где а – const>0 (2) Разлагаем потенциальную энергию в ряд Тэйлора, будем иметь где значения функции П и ее производных при q=0, т. е. в равновесном положении системы.

и обозначая получим где с const (3) В соответствии с теоремой Лагранжа Дирихле предположим, что потенциальная энергия П имеет при q=0 минимум. А это требует, чтобы с>0. (2) и (3) (1), получим уравнение Обозначив где λ вещественное постоянное число (4) получим дифференциальное уравнение малых колебаний системы с одной степенью свободы (5)

Составим характеристическое уравнение для (5) к 2 + λ 2 =0 и найдем его корни k = ± iλ. Общее решение полученного дифференциального уравнения (5) запишется q = С 1 cosλt + C 2 sin λt , (6) где С 1, С 2 – произвольные постоянные. Note: Можно получить другой вид общего решения, если сделаем обозначения (7) и где α, β - произвольные постоянные, то (6) примет вид Постоянные произвольные С 1, С 2 определяются по начальным данным движения системы (8)

Подставляя эти значения произвольных постоянных в уравнение (6) получим формулу (9) которая представляет обобщенную координату q как функции времени. Очевидно, что произвольные постоянные α и β определяются соотношениями , (10) Чтобы получить представление о движении системы, , рассмотрим движение каждой отдельной материальной точки Мi системы. Обозначим декартовы координаты точки Мi через xi, yi, zi, . а координаты точки Аi через x 0 i, y 0 i, z 0 i. Величины (11) будем называть эти величины смещениями точки Мi по осям x, y, z. Представим координаты точки Мi xi, yi, zi как функции от обобщенной координаты q

Разложим эти функции по степеням малой величины q. xi=x 0 i+Li(q)q, yi=y 0 i+Pi(q)q, zi=z 0 i+Ni(q)q, (11 а) где Li, Pi, Ni постоянные величины. (11 а) (11), получим выражения для смещений точек системы по осям координат представленные через обобщенную координату q. (12) Чтобы получить уравнения движения точки Мi в декартовых координатах, остается подставить в этих формулах вместо q выражение (8). Тогда получим соотношения (13) которые являются уравнениями собственных колебаний системы в декартовых координатах.

Из этих уравнений (13) мы можем вывести следующие заключения, характеризующие собственные колебания системы с одной степенью свободы: 1) Собственные колебания системы—колебания гармонические. 2) Исключая время из уравнений (13), получим или Это — уравнения прямой, проходящей через точку Аi, т. е. через равновесное положение точки Мi. Следовательно, каждая точка системы совершает прямолинейное движение по прямой, проходящей через ее равновесное положение. 3) Частота собственных колебаний λ определяется формулой (14)

Эта частота λ называется собственной частотой системы. Из ее определения видно, что собственная частота системы не зависит от начальных условий. Период Т собственных колебаний системы определяется формулой и также не зависит от начальных условий. 4) αLi , αPi , αNi амплитуды колебаний точек Мi, по осям соответственно; β - начальная фаза. Так как α и β - произвольные постоянные, зависящие от начальных условий движения, то очевидно, что амплитуды колебаний точек системы, а также начальная фаза зависят от начальных условий Но начальные условия влияют на амплитуды только через посредство множителя α, общего для всех точек системы. Отсюда следует, что отношения амплитуд различных точек системы, от начальных условий не зависит.

5) Как видно из решения фаза λt + β также является общей для всех точек системы, т. е. все точки системы всегда находятся в одной фазе. Это означает, что в процессе вибрации все точки системы одновременно проходят через свои положения равновесия (в моменты, когда sin(λt + β) = 0) и одновременно достигают максимального отклонения от положения равновесия (в моменты, когда sin(λt + β)=1).

Затухание собственных колебаний под действием диссипативных сил Также как и в предыдущем параграфе будем рассматривать систему: 1. с одной степенью свободы 2. состоящая из материальных точек 3. обобщенную координату системы обозначим по прежнему через q 4. рассмотрим собственные колебания системы имеющие потенциал 5. к системе приложены силы + 6. на систему действуют диссипативные силы (силы сопротивления Будем изучать малые колебания системы около устойчивого равновесного положения q = 0. Введем обозначения: скорости точек системы. Положим, что где постоянные величины.

Дифференциальное уравнение движения системы в данном случае будет иметь вид (15) где Т кинетическая энергия; П потенциальная энергия; Q обобщенная сила сопротивления, соответствующая силам Вычислим величину Q. Для этого обозначим проекции силы на оси декартовых координат через и будем иметь: (16) (16 а) (11 а) (17)

(17) и (11 а) (16), получаем окончательно к Поэтому (18) (2), (3), (18) (15), получим (19) Полагая (20) получим уравнение движения в виде (21) Умножим уравнение (19) на =

= поэтому это соотношение можно представить в виде Введем обозначение Тогда Величина R называется функцией рассеяния.

Добавление вынужденных колебаний Будем рассматривать систему: 1. с одной степенью свободы 2. состоящая из материальных точек 3. обобщенную координату системы обозначим по прежнему через q 4. рассмотрим собственные колебания системы имеющие потенциал 5. к системе приложены силы 6. на систему действуют диссипативные силы (силы сопротивления) + 7. на систему действуют возмущающие силы изменяющиеся с течением времени по наперед заданному закону.

Дифференциальное уравнение движения системы в этом случае будет иметь вид (22) где S—обобщенная возмущающая сила, величина которой определяется формулой где проекции силы S на оси декартовых координат или являются заданными функциями времени Разделив уравнение (22) на а и введя прежние обозначения (20), получим уравнение движения в виде: (23)

Для интегрирования уравнения (23) применим способ вариации произвольных постоянных. Этот способ заключается в следующем: 1. Записываем соответствующее однородное уравнение при ν<λ Оно имеет общее решение где А и В – const. λ 1 Тогда общее решение однородного уравнения примет вид (24) 2. Найдем теперь общий интеграл неоднородного уравнения (23) в виде соотношения (24). НО будем рассматривать в нем А и В, как функции времени, которые нам необходимо найти. Найдем и Пусть выполняется условие (25)

тогда формула для (26) Вторая производная (24) по t запишется (24), (26), (27) (23), находим (28) Решая уравнения (25) и (28) относительно или где произвольные постоянные. и получим:

Подставляя эти значения А и В в (24), получим (29) точек (12), получим соотношения, определяющие перемещения Если П=0, то формула (29) принимает вид: (30) где Тогда движение определится формулой собственные колебания вынужденные колебания
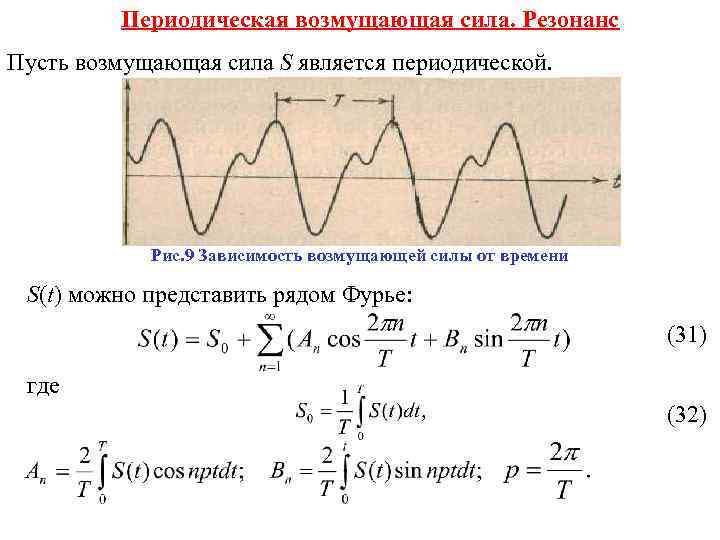
Периодическая возмущающая сила. Резонанс Пусть возмущающая сила S является периодической. Рис. 9 Зависимость возмущающей силы от времени S(t) можно представить рядом Фурье: (31) где (32)

называется n – ой гармоникой периодической функции S(t), а р – частота гармоники. Обозначая получим Тогда можем привести разложение (31) к виду Постоянные Кn и γn называются амплитудой и начальной фазой n-ой гармоники функции S(t). (31) (23), получим (34)

общее решение Общее = частное + соответствующего решение уравнения (34) однородного уравнения Общее решение соответствующего однородного уравнения (для случая малого сопротивления ( ν < λ )) имеет вид где α и β const Частное решение будем искать в виде разложения (35) где q 0, an, bn неизвестные коэффициенты, подлежащие определению (35) (34), получим

Левая часть полученного равенства будет равна правой при выполнении условий Откуда получаем (36)

Теперь подставляем частное решение (35) и общее решение однородного уравнения, получаем общее решение уравнения (34) (37) где α и β – const, q 0, an, bn параметры, определяемы формулами (36). постоянное отклонение системы от ее равновесного вынужденные колебания системы собственные колебания системы положения Частный случай: λ = ip, т. е. когда собственная частота системы λ равна частоте i ой гармоники возмущающей силы (i=1, 2, 3… целое число ) В этом случае, говорят, что наступает явление резонанса. Другими словами, мы имеем явление резонанса при всех тех значениях частоты возмущающей силы р, которые укладываются в формулу p =λ / i.

Все эти значения частоты р называются критическими частотами возмущающей силы. При р = λ резонанс вызывается первой гармоникой возмущающей силы и в этом случае возникает резонанс первого порядка. При р = λ / 2— в резонанс вступает вторая гармоника возмущающей силы и возникает резонанс второго порядка и т. д. Note: если в разложении возмущающей силы отсутствует гармоника какого либо определенного порядка, то будет отсутствовать и резонанс соответствующего порядка. Вынужденные колебания, происходящие в условиях резонанса, т. е. при одной из критических частот возмущающей силы, называются резонансными колебаниями.

Дифференциальные уравнения собственных колебаний систем с двумя степенями свободы Будем рассматривать систему: 1. состоящая из материальных точек 2. с двумя степенями свободы 3. обобщенные координаты обозначим q 1 и q 2 4. как и ранее исследуем малые колебания системы около ее равновесного положения 5. равновесное положение системы считаем устойчивым 6. будем считать, что в равновесном положении q 1=0, q 2=0 Составим дифференциальные уравнения малых колебаний нашей системы в координатах q 1 и q 2, используя уравнения Лагранжа второго рода (40) где Т и П кинетическая и потенциальная энергии системы.

В дальнейшем будем считать координаты q 1 и q 2, также обобщенные скорости и малыми величинами первого порядка малости. Кинетическая энергия вычисляется по формуле где функции от q 1 и q 2. Разложим функции q 1 и q 2 в ряды по степеням малых величин где значения функций при а многоточия заменяют члены, содержащие q 1 и q 2 в первой и более высоких степенях. Получаем

Для того чтобы всегда имело место неравенство T > 0 величины должны удовлетворять следующим условиям (согласно критерию Сильвестра) все диагональные миноры матрицы коэффициентов должны быть положительны (41) Перейдем к вычислению потенциальной энергии. Для вычисления потенциальной энергии, представим ее в виде разложения по степеням обобщенных координат где и т. д. значения функции П и ее производных при т. е. в равновесном положении системы.

Примем значение потенциальной энергии в равновесном положении системы П 0 за нуль Обозначив получим, что где постоянные величины. Ранее было сделано предположение, что равновесное положение устойчиво. Это, в соответствии с теоремой Дирихле, означает, что в положении равновесия потенциальная энергия П имеет минимум. Следовательно, значения потенциальной энергии в положениях системы, близких к равновесному, больше значения потенциальной энергии в равновесном положении. Но мы приняли значение потенциальной энергии системы в равновесном положении равным нулю. Отсюда следует, что при сделанных нами

предположениях во всех положениях системы, достаточно близких к равновесному, потенциальная энергия П должна быть величиной положительной. Для того чтобы это требование (П>0) было выполнено необходимо, как и ранее, использовать критерий Сильвестра Подставим полученные выражения для кинетической и потенциальной энергии в уравнение (40) (42) (43) дифференциальные уравнения малых колебаний консервативной системы с двумя степенями свободы.

Главные колебания и собственные частоты Будем искать частные решения уравнений (43) в виде (44) где (44) постоянные числа. (43), получим (45) Эти уравнения относительно постоянных α 1 и α 2 линейные и однородные, поэтому допускают решение, отличное от нуля только в том случае, когда определитель системы равен нулю

или (46) Это уравнение — квадратное относительно λ 2. Оба корня этого квадратного уравнения — вещественные и положительные. Извлекая квадратный корень из положительных чисел и при получим два вещественных значения и которых система (43) допускает частные решения вида (44), то есть уравнения системы (43) допускают два частных линейно независимых решения (47) (48)

Решения (47) и (48) системы называются ее главными колебаниями. Частоты главных колебаний λ 1 и λ 2 называются собственными частотами системы. Уравнение (46) имеет название уравнения частот. Полагая в уравнениях (45) Мы удовлетворим этим уравнениям, положив где α 1 произвольное число. Отсюда будем иметь:

Совершенно так же, обращаясь ко второму главному колебанию, получим где α 2 произвольное число. Таким образом уравнения главных колебаний (47) и (48) окончательно приводятся к виду: (49) (50) Таким образом, дифференциальные уравнения (43) имеют два частных решения (49) и (50). Так как это линейные уравнения, то, сумма этих частных решений, является новым решением (51)

(51) – общее решение уравнений (43). Чтобы получить отчетливое представление о движении системы, совершающей одно из главных своих колебаний, рассмотрим движение каждой отдельной материальной точки Мi, входящей в состав системы. Пусть xi, yi, zi декартовы координаты точки Мi; x 0 i, y 0 i, z 0 i координаты равновесного положения точки Мi; смещение точки Мi из ее равновесного положения (52) Выразим декартовы координаты xi, yi, zi как функции обобщенных координат q 1 и q 2 Разложим эти функции по степеням малых величин q 1 и q 2. Имея в виду, что постоянные члены в этих разложениях это значения т. е. в равновесном положении, получим: координат при

заданные постоянные величины, где а многоточия заменяют члены второго и высших порядков малости. Пренебрегая этими членами и вводя обозначения (52), будем иметь: Подставляя в полученные формулы вместо q 1 и q 2 их выражения из формул (49), получим уравнения первого главного колебания системы в декартовых координатах. (53)

Совершенно так же, заменяя выражения (49) обобщенных координат q 1 и q 2 выражениями (50), получим уравнения второго главного колебания в декартовых координатах. Из этих уравнений мы можем вывести следующие свойства главных колебаний системы: 1) Главные колебания системы колебания гармонические. 2) Исключая время из уравнений (53), получаем уравнения прямой, проходящей через равновесное положение точки Мi. Следовательно, если система совершает одно из своих главных колебаний, то каждая точка системы совершает прямолинейное движение по прямой, проходящей через ее равновесное положение.

3) Собственные частоты λ 1 и λ 2 определяются как корни уравнения частот (46) собственные частоты системы не зависят от начальных условий. То же можно сказать про периоды главных колебаний Т 1 и Т 2, так как 4) Постоянные α 1 и β 1, входящие в формулы (53), являются произвольными постоянными, зависящими от начальных условий движения. Следовательно, если система совершает одно из главны колебаний, то амплитуды колебаний точек системы, а также начальная фаза колебания зависят от начальных условий. НО отношения амплитуд различных точек системы от начальных условий не зависит. 5) Фаза одинакова для всех точек системы. Следовательно, когда система совершает одно из главных колебаний, то все ее точки имеют одинаковую фазу и одновременно проходят через свои равновесные положения и одновременно достигают максимальных отклонений от положения равновесия.

ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ СИСТЕМ 1. Метод разложения по малому параметру Суть метода: состоит в разложении искомого решения нелинейного уравнения в ряд по степеням малого параметра Преимущества метода: 1) метод можно применять даже при отсутствии каких либо предварительных представлений об общем характере решения 2) метод разложения по малому параметру весьма полезен также при изучении теоретических вопросов чисто математического характера Недостатки метода: 1) громоздкость сопряженных с ним вычислений

Применим разложение (55) по малому параметру ε для получения гармонических решений уравнения (54) (55) Введем вместо t новую переменную θ при помощи равенства θ = ω t. Тогда уравнение (54) примет вид (56) Потребуем, чтобы функция х(θ) удовлетворяла следующим условиям: (57 а) где А – max x(t) (57 б) (57 в) Выберем ε = β (58)

Кроме функции х(t), необходимо представить в виде ряда по степеням β также частоту ω (59) Если подставим (58) и (59) в (56), получим разложение по степеням β, которое должно обращаться в нуль тождественно при любом β; следовательно должны быть равны нулю коэффициенты этого разложения при каждой степени β. Эти коэффициенты будут представлять собой линейные дифференциальные уравнения второго порядка для функций хi(θ), содержащие также и постоянные ωi. Для определения функций хi(θ) и постоянных ωi нужно использо вать условия (57), которые приводят к ряду условий (60 а) (60 б) (61) Будем предполагать, что (62)

(58), (59) и (62) (56), получим (63) Первый этап. Приравнивая нулю член нулевой степени относительно β, получим уравнение (64) Общее решение этого уравнения имеет вид (65) Из условий (60 а), (60 б) и (61) получаем (66) (67)

Второй этап. Продолжим дальше этот процесс, приравняв нулю коэффициент члена первого порядка в уравнении (63). Это приводит к дифференциальному уравнению относительно x 1(θ) (69) (67) (69) (70) Полагаем Отсюда получаем значение ω1 (71)

Общее решение уравнения (70) может быть теперь представлено в виде (72), получаем (73) В силу условий (61 б) и (61 в) необходимо, чтобы (74) Таким образом, окончательно получаем решение

Итак, искомое общее решение (58) и (59) с точностью до членов первой степени относительно β включительно будет иметь вид (75) (76)

2. Метод Ван-дер-Поля Метод Ван дер Поля используется при описании функционирования автономных динамических систем с одной степенью свободы. Метод Ван дер Поля используется для изучения систем, уравнение движения которых имеет вид (77) где μ>0 - это малый безразмерный коэффициент. Введем в рассмотрение безразмерное время τ=ωt. Тогда уравнение (77) примет вид (78) где Если ввести обозначение то уравнение (78) можно представить в виде двух уравнений первого порядка:

(79) Суть метода Ван – дер – Поля состоит в том, что вместо уравнений (79), рассматриваются укороченные уравнения, которые позволяют с достаточной для практического применения точностью получить приближенное решение исходных уравнений. На фазовой плоскости x y уравнение интегральных кривых будет (80) 1. μ = 0, тогда (80) принимает вид системы (78) служит соотношение В этом случае решением (81) в котором а и b — постоянные интегрирования. 2. μ ≠ 0. Будем искать решение уравнения (78) в виде (81), считая коэффициенты а и b функциями времени.

Фактически решается задача определения величин а(τ) и b(τ). Тогда (82) Из выражения (81) видно, что при заданном x функции а и b недостаточно определены, поэтому наложим на них ограничение, заключающееся в том, что производная от x по τ должна иметь такой же вид, как при постоянных а и b. Следовательно, (83) (84) Дифференцируя, выражение (83) по τ, получаем (85) (83) и (85) (78)

(86) Уравнения (84) и (86) представляют собой систему уравнений для и определения Решая эту систему, будем иметь (87) Полученные уравнения — это уравнение (78), преобразованное к новым переменным. Из выражений (87) следует, что производные и при достаточно малом μ достаточно малы, и можно считать, что функции а и b являются медленно меняющимися функциями времени. Поэтом будем считать, что: 1. что функции а и b меняются столь медленно, что их изменением за один период колебаний исходной системы можно пренебречь;

2. будем также считать, что и имеющие порядок μ, в течение одного периода постоянны. Поэтому не будет большой ошибкой, если заменим правые части системы (87) их средними значениями за период. (88) Вводя обозначения (89) перепишем (88) в виде

(89 а) Эти уравнения называются «укороченными» или уравнениями Ван-дер-Поля. Из уравнений (89 а) получается, что (90) Уравнение (90) позволяет исследовать поведение интегральных кривых на плоскости аb. Чтобы исследовать поведение интегральных кривых на плоскости xy, перейдем к полярным координатам в системе уравнений (89). Введем новые переменные: (91)
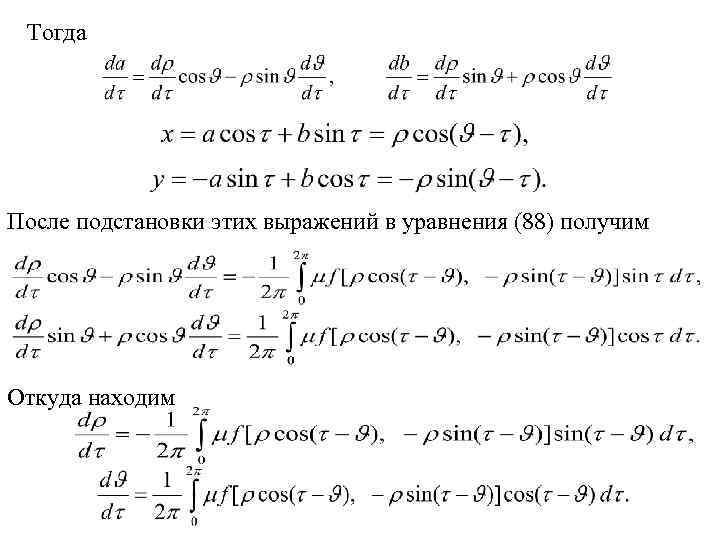
Тогда После подстановки этих выражений в уравнения (88) получим Откуда находим

Вводим замену ξ=τ- , окончательно получим (92) где (93) Первое уравнение системы (92) не зависит от и фазовая плоскость для него вырождается в прямую. Состояния равновесия этого уравнения располагаются на фазовой прямой. Координаты положений равновесия уравнения (94) являются корнями уравнений (95)

Пусть ρ=ρ0 являются корнем уравнения (95). Рассмотрим отклонение u изображающей точки от состояния равновесия Уравнение (94) при этом примет вид Разлагаем функцию в ряд по степеням u: + члены высших порядков малости. Ограничиваясь членами с первой степенью u, получим уравнение первого приближения Если Ф' (ρ0) <0, то состояние равновесия устойчиво, так как при этом и и —> 0. Если Ф' (ρ0 ) > 0, то состояние равновесия неустойчиво, так как в этом случае величина и увеличивается.

Если проинтегрировать уравнение (94), то можно получить закон движения изображающей точки по фазовой прямой Второе уравнение системы (92) Если Ψ(ρ) = 0 и — постоянное число на плоскости аb (рис. 10) все интегральные кривые представляют собой прямые, проходящие через начало координат. Движение изображающей точки по всем этим прямым происходит одинаково. Состояния равновесия на плоскости аb целиком заполняют дуги окружностей, радиусы которых являются корнями уравнения (95).
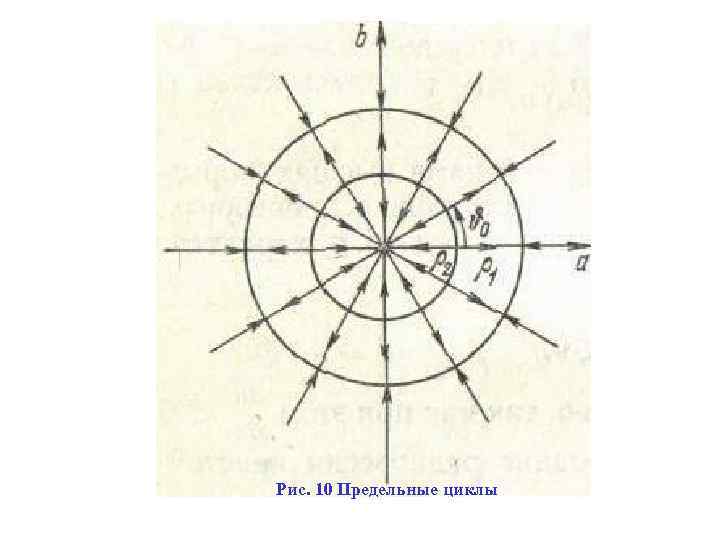
Рис. 10 Предельные циклы

Рассмотрим характер процесса на плоскости xy. В соответствии с формулами (81), (83) и (91) получим Для какого либо состояния равновесия ρ=ρк значения координат в этой плоскости будут Это означает, что на плоскости xy имеется замкнутая интегральная кривая — круговой предельный цикл Если ρк соответствует устойчивому состоянию равновесия, то на плоскости xy — создается устойчивый предельный цикл; все соседние интегральные кривые — спирали, накручивающиеся на этот предельный цикл. Если ρк соответствует неустойчивому состоянию равновесия, то на плоскости xy — создается неустойчивый предельный цикл.

3. Метод построения асимптотических решений В данном параграфе излагается метод построения асимптотических приближений для описания колебаний, определяемых дифференциальным уравнением вида (96) где ε малый положительный параметр. Если ε=0 (нет возмущений), то колебания, описываемые уравнением, будут чисто гармоническими с постоянной амплитудой а и равномерно вращающимся фазовым углом ψ Если ε≠ 0 (присутствуют нелинейные возмущения), то существует зависимость мгновенной частоты от амплитуды.

Принимая все это во внимание, будем искать общее решение рассматриваемого уравнения (96) в виде разложения (97) где периодические функции угла ψ с периодом 2π, а величины а, ψ – функции времени, определяемые дифференциальными уравнениями (98) Итак, перед нами возникает задача подбора соответствующих выражений для функций таким образом, чтобы выражение (97), в которое вместо a и Ψ будут подставлены функции времени, определенные уравнениями (98), оказалось бы решением исходного уравнения (96).

Формулировка задачи: найти такие функции (99) чтобы выражение (97), в котором функции времени а и Ψ определяются «уравнениями т-го приближения» (98), удовлетворяло уравнению (96) с точностью до величин порядка малости εm+1. Наложим дополнительные условия на выражения (99) – условия т. е. будем так отсутствия первой гармоники в выражениях определять эти периодические функции фазового угла, чтобы выполнялись равенства (100) Дифференцируя соотношение (97) и с учетом (98) определяя соответствующие вторые производные от а и ψ по времени, получим
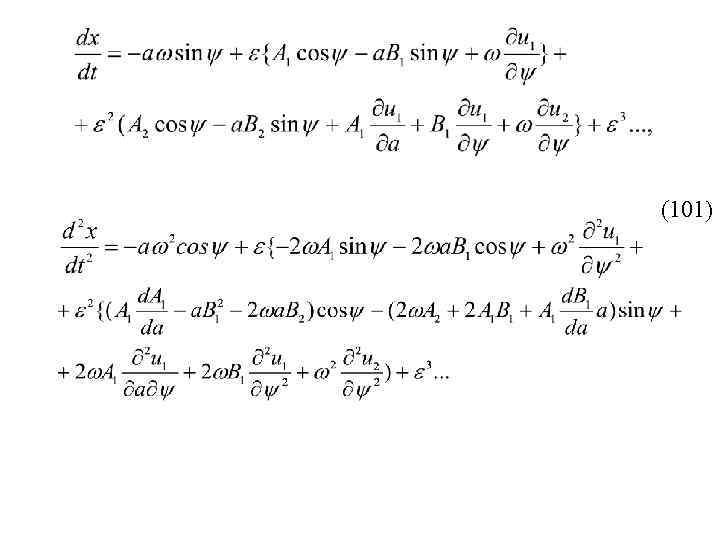
(101)

Правую часть уравнения (96), учитывая соотношения (97) и (101) можно представить в виде: (102) (97), (101) и (102) (96) Очевидно, для того чтобы рассматриваемое выражение (97) удовлетворяло исходному уравнению (96) с точностью до величин порядка малости εm+1, необходимо приравнять коэффициенты при одинаковых степенях ε в правых и левых частях полученного уравнения до членов m го порядка включительно. В результате получим следующие уравнения:
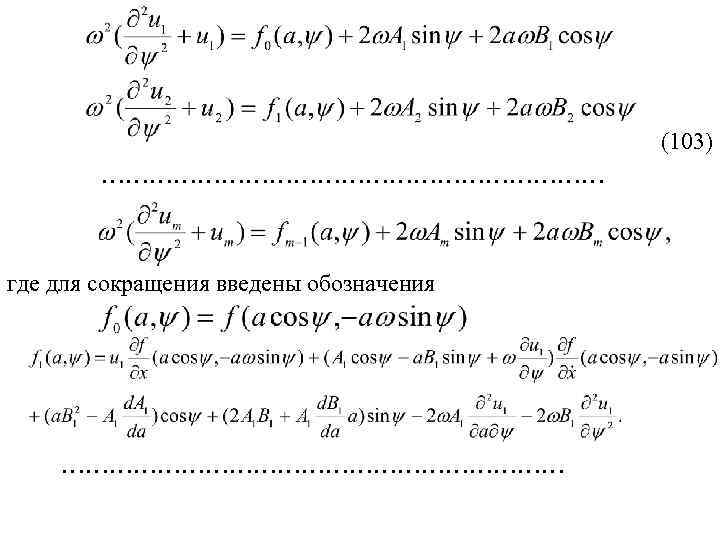
(103) …………………………… где для сокращения введены обозначения ……………………………

Для того чтобы найти явное выражение для надо найти до k-ro номера включительно. выражения Сначала найдем из первого уравнения системы (103). Для этого используем разложения Фурье для функций и (104) первое уравнение (103), получим выражение В получившемся выражении приравниваем коэффициенты при одинаковых гармониках

(105) Таким образом, однозначно определяются и а также все гармонические компоненты функции . Однако в силу дополнительных условий кроме первых и (100) эта функция не содержит первой гармоники, поэтому И, следовательно, (106)

Определив полностью выражение для Для нахождения получаем явное разложим в ряд Фурье и воспользовавшись вторым из уравнений (103) и условием (100), совершенно аналогично находим Таким образом, получается процесс для последовательного однозначного определения интересующих нас величин (101).

Изложенный метод позволяет определить до какого угодно высокого значения индекса n (при условии отсутствия в функциях первой гармоники) и тем самым построить приближенные решения, удовлетворяющие рассматриваемому уравнению (96) с точностью до величин сколь угодно высокого порядка малости по отношению к ε.
презентация_Теория колебаний.ppt