
Глава 3. Точка p p Выше было установлено, что одна проекция точки не определяет её положения в пространстве Чтобы установить это положение, требуются дополнительные условия. Например, дана прямоугольная проекция на горизонтальной плоскости проекций и указано удаление этой точки от плоскости числовой отметкой На этом основан метод проекций с числовыми отметками Плоскость проекций принимается за «плоскость нулевого уровня» , и числовая отметка считается положительной, если точка в пространстве выше плоскости нулевого уровня, и отрицательной, если точка ниже этой плоскости ( для строительных и архитектурных чертежей) 11. 02. 2018 1

Положение точки в пространстве p Определение положения точек в пространстве производится по их прямоугольным проекциям на двух и более плоскостях проекций n p Слово «прямоугольный» часто заменяют словом «ортогональный» , образованным из слов древнегреческого языка, обозначающих «прямой» и «угол» Все пространственные объекты ориентируют относительно пространственной декартовой системы координатных осей – системы трех взаимно перпендикулярных координатных плоскостей 11. 02. 2018 2
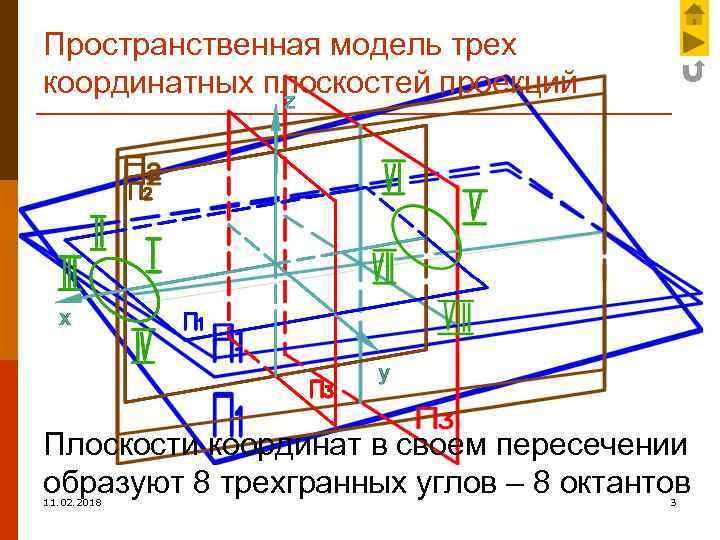
Пространственная модель трех координатных плоскостей проекций Плоскости координат в своем пересечении образуют 8 трехгранных углов – 8 октантов 11. 02. 2018 3
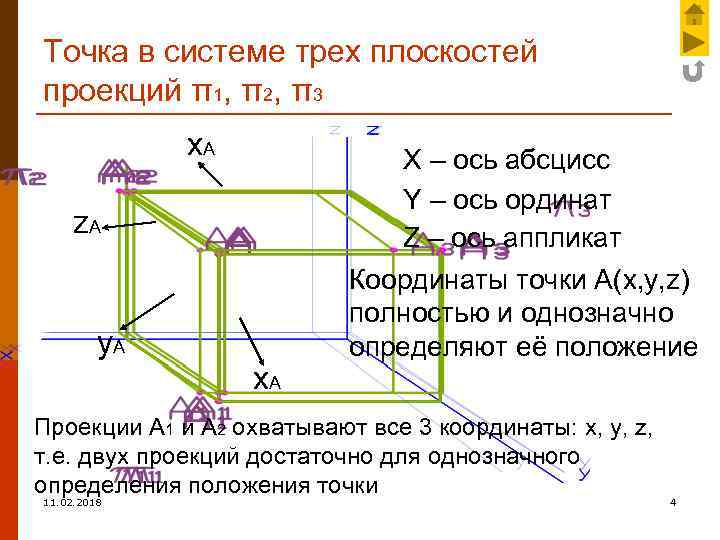
Точка в системе трех плоскостей проекций π1, π2, π3 x. A X – ось абсцисс Y – ось ординат Z – ось аппликат z. A y. A x. A Координаты точки А(x, y, z) полностью и однозначно определяют её положение Проекции А 1 и А 2 охватывают все 3 координаты: x, y, z, т. е. двух проекций достаточно для однозначного определения положения точки 11. 02. 2018 4
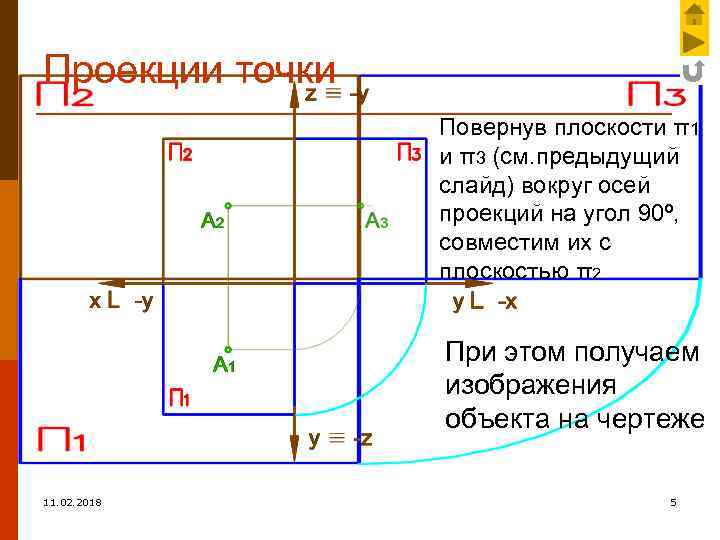
Проекции точки Повернув плоскости π1 и π3 (см. предыдущий слайд) вокруг осей проекций на угол 90º, совместим их с плоскостью π2 При этом получаем изображения объекта на чертеже 11. 02. 2018 5
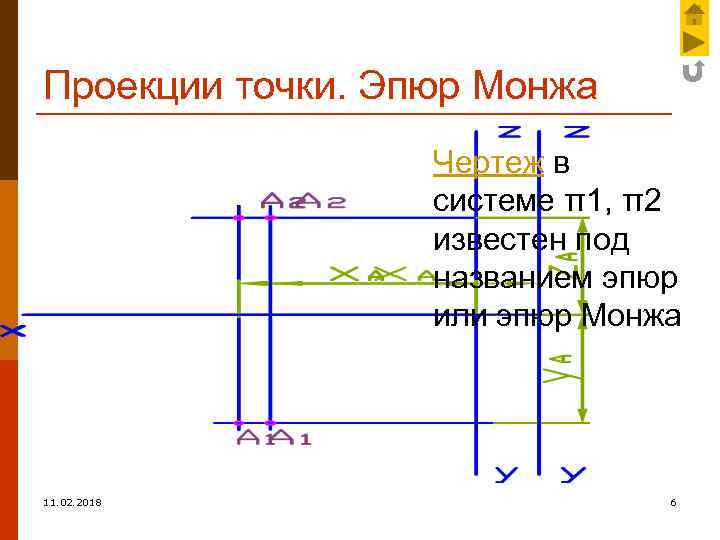
Проекции точки. Эпюр Монжа Чертеж в системе π1, π2 известен под названием эпюр или эпюр Монжа 11. 02. 2018 6

p В дальнейшем эпюр Монжа, а также проекционные чертежи, в основе которых лежит метод Монжа, будем называть одним словом - чертеж - и понимать это слово только в указанном смысле. В других случаях применения слова «чертеж» оно будет сопровождаться соответствующим определением (перспективный чертеж, аксонометрический чертеж и т. п. ) [3] 11. 02. 2018 7

Выводы p Ортогональное проецирование – прямоугольное, параллельное проецирование на три взаимно перпендикулярные плоскости – единственный способ построения машиностроительных чертежей 11. 02. 2018 8

Выводы p p Положение точки определяется её ортогональными проекциями на две плоскости По двум проекциям всегда можно построить третью 11. 02. 2018 9
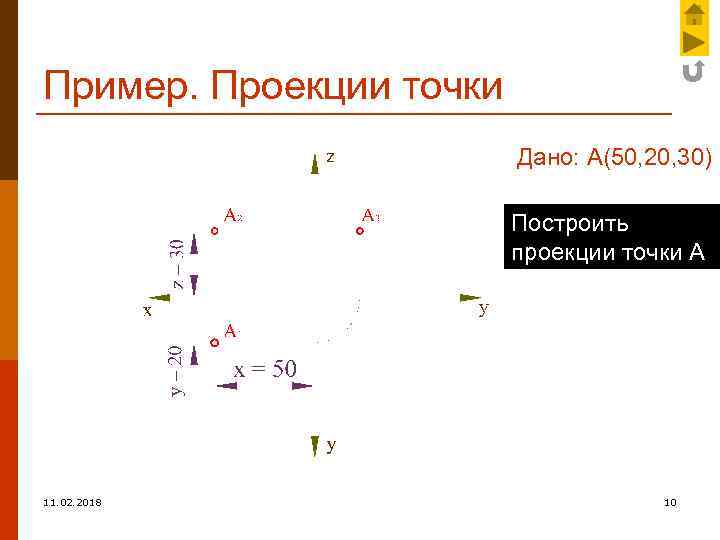
Пример. Проекции точки Дано: А(50, 20, 30) Построить проекции точки А 11. 02. 2018 10