ГЛАВА 3. НОРМИРОВАНИЕ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ n

ГЛАВА 3. НОРМИРОВАНИЕ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СРЕДСТВ ИЗМЕРЕНИЙ n Средство измерения (СИ) — это техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу ФВ, размер которой принимается неизменным (в пределах установленной погрешности) в течение известного интервала времени. Под метрологическими характеристиками (МХ) понимают такие характеристики СИ, которые позволяют судить об их пригодности для измерений в известном диапазоне с известной точностью. В отличие от СИ приборы или вещества, не имеющие нормированных МХ, называют индикаторами. СИ — это техническая основа метрологического обеспечения.

Меры — это СИ, воспроизводящие или хранящие физическую величину заданного размера. Меры бывают однозначные и многозначные. n Измерительные преобразователи — СИ, предназначенные для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения, но не доступной для непосредственного восприятия наблюдателем. n Измерительный прибор — СИ, предназначенное для переработки сигнала измерительной информации в другие, доступные для непосредственного восприятия наблюдателем формы. Различают приборы прямого действия (амперметры, вольтметры, манометры) и приборы сравнения (компараторы). По способу отсчета измеряемой величины СИ делятся на показывающие (аналоговые, цифровые), регистрирующие (на бумажную или магнитную ленту) и т. п. n Измерительная установка — совокупность функционально объе диненных СИ и вспомогательных устройств, расположенных в одном месте. n Измерительная система — это комплекс СИ и вспомогательных устройств с компонентами связи, предназначенный для выработки сигналов измерительной информации в форме, удобной для автоматической обработки, передачи и использования в автоматических системах управления. n

Для оценки пригодности СИ к измерениям в известном диапазоне с известной точностью вводят МХ СИ. На практике наиболее распространены следующие МХ СИ. n Диапазон измерений— область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ. n Предел измерения — наибольшее или наименьшее значение диапазона измерения. n Цена деления шкалы — разность значений величин, соответствующих двум соседним отметкам шкалы. Приборы с равномерной шкалой имеют постоянную цену деления, а с неравномерной — переменную. В этом случае нормируется минимальная цена деления. n Чувствительность — отношение изменения сигнала ∆у на выходе СИ к вызвавшему это изменение изменению ∆х сигнала на входе S = ∆у/∆х. n Порог чувствительности— наименьшее значение измеряемой величины, вызывающее заметное изменение показаний прибора. n Величину, обратную чувствительности, называют постоянной прибора С = 1/S. n Вариация (гистерезис) — разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измерений величины и неизменных внешних условиях:

n n Зависимость между выходным и входным сигналом СИ, полученную экспериментально, называют градуировочной характеристикой, которая может быть представлена аналитически, графически или в виде таблицы. Погрешность СИ — разность между показаниями СИ и истинными (действительными) значениями ФВ. Существуют три способа нормирования основной погрешности СИ: • нормирование пределов допускаемой абсолютной (±∆) или приведенной (±γ) погрешностей, постоянных во всем диапазоне измерения; • нормирование пределов допускаемой абсолютной (±∆) или относительной (±σ) погрешностей в функции измеряемой вели чины; • нормирование постоянных пределов допускаемой основной погрешности, различных для всего диапазона измерений одного или нескольких участков. Следует учесть, что: 1) дополнительная погрешность имеет такой же вид, что и основная; 2) дополнительные погрешности, вызванные различными влияющими факторами, должны нормироваться раздельно. В общем виде суммарная абсолютная погрешность СИ при влияющих факторах:

n Абсолютная погрешность —разность между показанием х СИ и действительным значением хд измеряемой величины Абсолютная погрешность выражается в единицах измеряемой ФВ и может быть задана: а) одним числом (линия 1 на рис. 3): ∆ = ±a; б) в виде линейной зависимости (линии 2 и 3): ∆ = ±Ьх; ∆ = ± (а + Ьх); в) в виде функции ∆ =f(x) или графика, таблицы. . Если значение погрешности не изменяется во всем диапазоне измерения (линия 1), то такая погрешность называется аддитивной (или погрешностью нуля). n Если погрешность изменяется пропорционально измеряемой величине (линия 2), то ее называют мультипликативной. Относительная погрешность: n

Нормирование погрешностей с аддитивной и мультипликативной составляющими

Различают равномерные (рис. 5, а, б, в, г) и неравномерные шкалы. Последние делятся на существенно неравномерные и степенные. n Существенно неравномерная шкала с сужающимися делениями, на которой отметка, соответствующая полусумме начального и конечного значения рабочей части шкалы, расположена между 65 и 100% длины этой рабочей части (рис. 5, д). n Степенная шкала с расширяющимися или сужающимися делениями, но не попадающими под определение существенно неравномерных (рис. 5, е). Тогда нормирующее значение х. N, принимается равным: • конечному значению рабочей части шкалы х. N= хк, если нулевая отметка — на краю или вне рабочей части шкалы (равномерная шкала рис. 5, а — х. N = 50; рис. 5, б — х. N = 55; степенная шкала — х. N = 4 на рис. 5, е); • сумме конечных значений шкалы (без учета знака), если нулевая отметка — внутри шкалы рис. 5, в, х. N = 20+20=40; рис. 5, г, х. N= 20+40=60; • длине шкалы, если она существенно неравномерна. В этом случае поскольку длина выражается в миллиметрах, то абсолютную погрешность надо выражать также в миллиметрах (рис. 5, д); • номинальному значению х, если СИ предназначено для измерения отклонения измеряемой величины от номинального значения. n Специфическим видом погрешности цифровых СИ и дискретных преобразователей является погрешность квантования, которая вносится округлением значения измеряемой величины и номинального значения.

При технических измерениях можно пользоваться более грубым нормированием — присвоением СИ определенного класса точности по ГОСТ 8. 401— 80. n Класс точности — это обобщенная МХ, определяющая различные свойства СИ. ГОСТ 8. 401— 80 устанавливает несколько способов назначения классов точности. При этом в основу заложены следующие положения: • в качестве норм служат пределы допускаемых погрешностей, включающие систематические и случайные составляющие; • основная δосн и все виды дополнительных погрешностей δдоп нормируются порознь. ГОСТ 8. 401— 80 в качестве основных устанавливает три вида классов точности СИ: ь для пределов допускаемой абсолютной погрешности в единицах измеряемой величины или делениях шкалы; ь для пределов допускаемой относительной погрешности в виде ряда чисел δ = ±A·10 n, ь для пределов допускаемой приведенной погрешности с тем же рядом: γ = ±А·10 n.

Соотношение классов точности γ и коэффициентов с/d Класс точности 1, 0 1, 5 2, 5 4, 0 Коэффициенты c/d 4/1, 0 6/1, 5 10/2, 5 15/4, 0

Оценка рабочей зоны СИ Номинальная функция преобразования ЦСИ

Формулы вычисления погрешностей и обозначение классов точности СИ Вид по греш ности Абсо лют ная Отно си тель ная Формула Примеры пределов допускаемой погрешности СИ, рекомендуе мые к на СИ обозначени ю таким способом Обозначение класса точности в НТД Класс точности N или класс точности III Класс точ ности 0, 5 N Меры III То же 0, 5 0, 02/ 0, 01 Мосты, дели тели, изм. трансформа торы и т. д. Цифровые СИ, магазины емкостей

Класс точ ности С или класс Точности II При ве ден ная C а) при х. N=x. K Класс точ ности 1, 5 Аналоговые СИ; если х. N в единицах величины б) х. N длина шкалы или ее части Класс точ ности 0, 5 Омметры; если х. N определяет ся длиной шкалы или ее части II Цифровые частотоме меры, мосты сопротивле ний

Под цифровыми СИ (ЦСИ) будем понимать приборы, предусматривающие либо цифровой отсчет показаний, либо цифровое преобразование измерительной информации: ЦИУ (ЦИП) — цифровые измерительные устройства (приборы); ИВК — информационные вычислительные комплексы; АЦП — аналогоцифровые измерительные преобразователи; ЦАИ — цифроаналоговые измерительные преобразователи. В общем случае показание отсчетного устройства ЦСИ где q — шаг квантования в единицах измеряемой величины. Константа q — важнейшая метрологическая характеристика ЦСИ, устанавливающая связь между измеряемой величиной х и выходным кодом и определяющая чувствительность ЦСИ (S= 1/q). Величину q называют еще номинальной ценой единицы наименьшего разряда кода. Обычно n При анализе погрешностей измерения ЦСИ рассматривают два режима — статический и динамический. n Основная метрологическая характеристика линейного ЦСИ — номинальная функция преобразования Среднее квадратическое отклонение:

Формирование реальной погрешности ЦСИ Погрешность квантования ЦСИ

n Абсолютная погрешность квантования: n Относительная погрешность квантования: n Приведенная погрешность квантования: n Время несинхронизации — это время между моментами, соответствующими началу интервала и переднему фронту одного из счетных импульсов. . При измерении интервала времени функция преобразования ЦСИ: Поскольку в таких СИ , то

Погрешность несинхронизации ЦСИ Методическая погрешность ЦСИ при отсутствии синхронизации

n Инструментальная погрешность: n Случайная составляющая основной статической погрешности: или n Результирующая погрешность АЦП представляет собой сумму статических и динамических погрешностей: n А ее дисперсия равна: n Шаг квантования определяется как:

Номинальная и реальная функции преобразования (а) и функция погрешности (Б) АЦП Гистерезис ЦСИ

Все виды СИ можно классифицировать: • меры и цифроаналоговые преобразователи (ЦАП); • измерительные и регистрирующие приборы; • аналоговые (АП) и цифровые измерительные преобразователи (ЦИП). В комплекс НМХ ЦСИ входят: I. Характеристика, позволяющая определять значение измеряемой величины по выходному сигналу (показанию или коду) ЦСИ. II. Характеристики, позволяющие рассчитать (оценить) составляющие погрешности измерения из за ЦСИ в нормальных условиях. III. Характеристики, позволяющие рассчитать (оценить) составляющие погрешность измерений, обусловленные ЦСИ в рабочих условиях эксплуатации. Наиболее распространенными формами записи класса точности ЦСИ являются: 1) 3) 2)

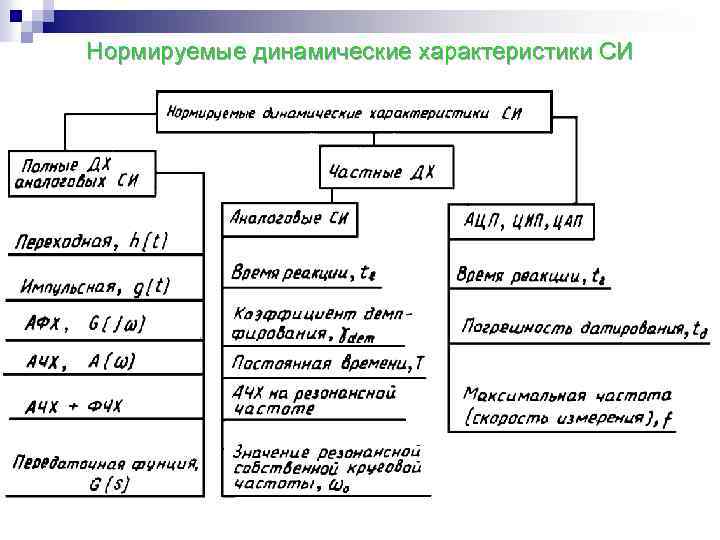Нормируемые динамические характеристики СИ

Практические рекомендации по расчету инструментальной погрешности СИ в эксплуатации сводятся к следующему: • при технических измерениях оценка погрешностей измере ний должна быть произведена до проведения самих измерений по нормированным МХ. По НМХ может быть рассчитана только ин струментальная составляющая. Для этого предусмотрены модели погрешности I; • практически для серийно выпускаемых СИ редко нормиру ется комплекс характеристик, достаточный для расчетов по мето дике РД 50— 453— 84. Как правило, в эксплуатации документы на СИ содержат данные по одному из вариантов: ь предел допускаемой основной погрешности; ь предел допускаемой систематической составляющей основной погрешности и предел допускаемой СКО случайной составляющей основной погрешности; ь предел допускаемой основной погрешности и предел допускаемой СКО случайной составляющей основной погрешности.