Глава 3 Аналитическая геометрия на плоскости 1

Глава 3. Аналитическая геометрия на плоскости § 1. Способы задания прямой на плоскости

Рекомендуемая литература: l l Александров П. С. Лекции по аналитической геометрии. – М. : Наука, 1968. – 260 с. Клетеник Д. В. Сборник задач по аналитической геометрии. – М. : Наука, 1968. – 320 с. Математика для техникумов. Геометрия: учебник / М. И. Каченовский и др. – М. : наука, 1989. – 320 с. Уравнения прямых на плоскости. Методические указания к практическим занятиям. Сургут, 2007.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т. е. А 2 + В 2 0. Это уравнение первого порядка называют общим уравнением прямой.

Любой ненулевой вектор , параллельный данной прямой называют направляющим вектором этой прямой. Любой ненулевой вектор , перпендикулярный данной прямой называют нормальным вектором этой прямой.

Неполное уравнение прямой Уравнение прямой называют неполным, если один из его коэффициентов равен 0. 1) C = 0, А 0, В 0 – прямая проходит через начало координат; 2) А = 0, В 0, С 0 { By + C = 0}- прямая параллельна оси Ох; 3) В = 0, А 0, С 0 { Ax + C = 0} – прямая параллельна оси Оу; 4) В = С = 0, А 0 – прямая совпадает с осью Оу; 5) А = С = 0, В 0 – прямая совпадает с осью Ох.

Прямая на плоскости может быть задана, как прямая, проходящая через: l l l точку М 0 параллельно вектору (рис. 1); точку М 0 перпендикулярно вектору (рис. 2); точки М 1 и М 2 (рис. 3); М 2 М • М М 1 • Рис. 1 Рис. 2 Рис. 3

П. 1. Уравнение прямой, проходящей через точку М 0 параллельно вектору. Пусть дан вектор и точка М 0(x 0, y 0). Тогда уравнение прямой, проходящей через эту точку параллельно данному вектору примет вид: - каноническое уравнение прямой

П. 2. Уравнение прямой, проходящей через точку М 0 перпендикулярно вектору. Пусть дан вектор и точка М 0(x 0, y 0). Тогда уравнение прямой, проходящей через эту точку перпендикулярно данному вектору примет вид:

П. 3. Уравнение прямой, проходящей через точки М 1 и М 2. Пусть даны точки М 1(х1, y 1) и М 2(x 2, y 2). Тогда уравнение прямой, проходящей через эти точки примет вид:

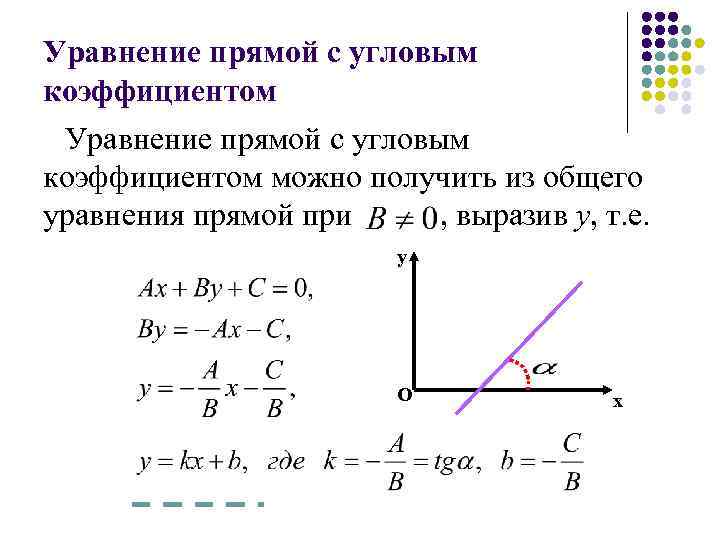Уравнение прямой с угловым коэффициентом можно получить из общего уравнения прямой при , выразив y, т. е. y О x

Уравнение прямой в отрезках Из общего уравнения прямой можно получить уравнение прямой в отрезках, если у а О b х

Параметрическое уравнение прямой Пусть на прямой выбрана точка М 0(х0, у0) и вектор ее направляющий вектор. Тогда уравнение данной прямой можно задать в параметрическом виде где t – параметр, который принимает любое действительное значение.