Глава 1. Элементы теории массового обслуживания 1. 2. Описание и основные свойства случайных потоков 1
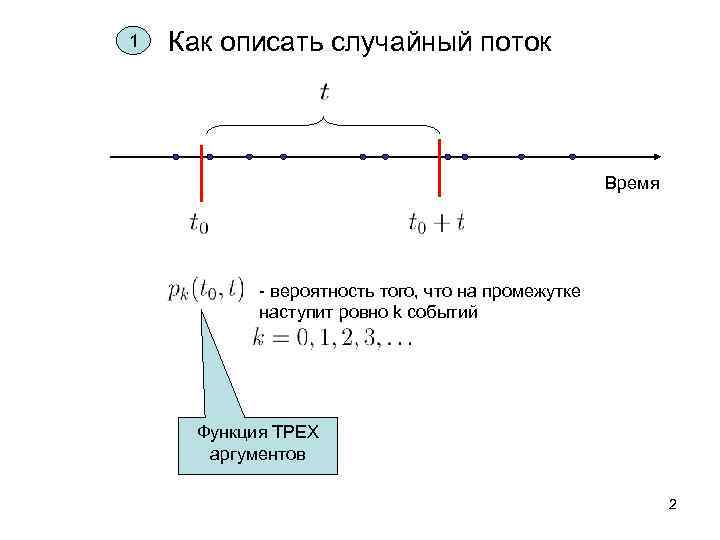
1 Как описать случайный поток Время - вероятность того, что на промежутке наступит ровно k событий Функция ТРЕХ аргументов 2
2 Основные свойства случайных потоков а) Стационарность б) Ординарность в) Отсутствие последействия 3
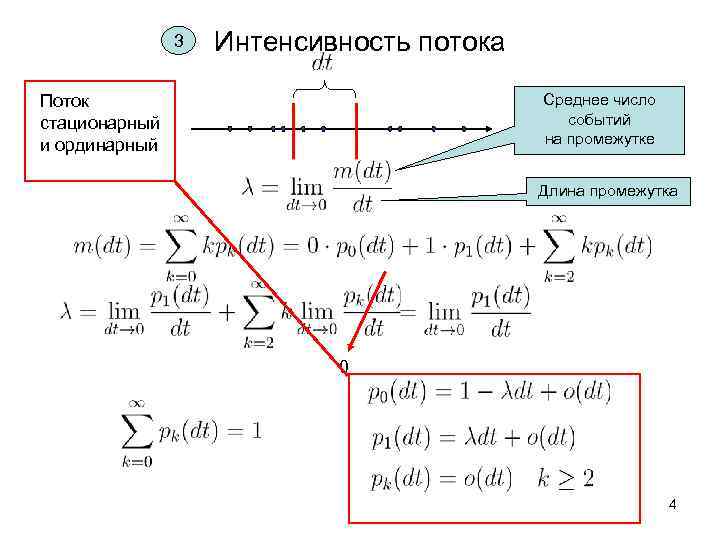
3 Интенсивность потока Среднее число событий на промежутке Поток стационарный и ординарный Длина промежутка 0 4
4 Простейший (пуассоновский) поток • Стационарный Простейший поток • Ординарный • Без последействия 0 5
4 Простейший (пуассоновский) поток 0 6
5 Отступление: преобразование Лапласа Варианты: преобразование Карсона, Хэвисайда, Карсона. Лапласа и т. п. Действительная функция (оригинал) Прямое преобразование Примеры Комплексная функция (образ) Обратное преобразование Свойства 7
6 Распределение числа событий в простейшем потоке Распределение Пуассона 8
7 Распределение интервалов между событиями в простейшем потоке - случайная величина, равная интервалу между двумя соседними событиями - (интегральная) функция распределения - плотность распределения вероятность того, что в интервале не произойдет ни одного события при условии, что оно произошло в начале промежутка. Так как поток без последействия, то эта вероятность равна безусловной вероятности наступления 0 событий на интервале Справедливо обратное утверждение! 9
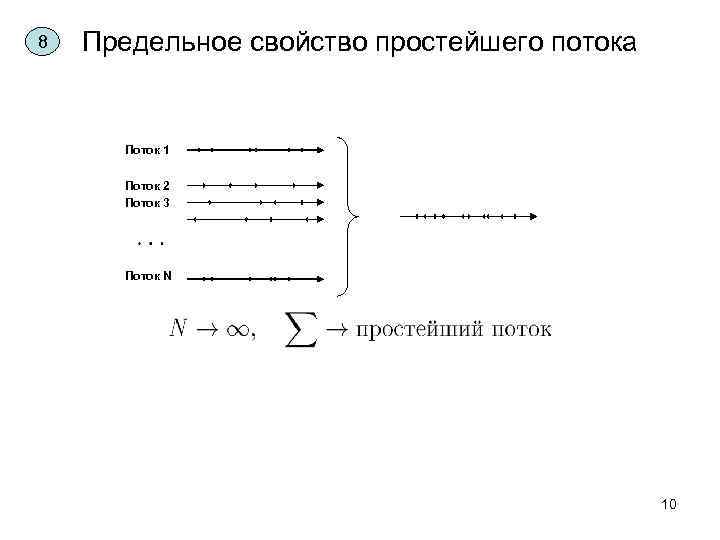
8 Предельное свойство простейшего потока Поток 1 Поток 2 Поток 3 Поток N 10
Скачать презентацию Глава 1 Элементы теории массового обслуживания 1 2
Queueing_Theory_2.ppt